可靠度在岩土工程中的应用
2021-06-06刘伟
刘伟
(国家管网集团西南管道有限责任公司 兰州输油气分公司,甘肃 兰州 730060)
0 引言
可靠度的研究始于20世纪30年代,当时主要是围绕飞机时效进行研究。可靠度在工程结构设计中的应用大概从1940年代开始。1956年,卡萨格兰提出了土工和基础工程的计算风险问题,20世纪60年代,G.G.Meyerhof,E.H.Vanmarcke等发表了一系列论著,奠定了土工可靠度方法的基 础[1]。我国对可靠度的研究晚于西方国家,20世纪50年代中期开始对可靠度进行研究[1−2]。1989年建设部下达了以长江科学院和同济大学为主,进行“岩土工程可靠度可行性研究”联合公告,将随机场理论引进沿途可靠度研究中,并从应用基础研究到专项实用研究。近年来,随着科技的进步,计算机技术的发展及理论的完善,各种可靠度分析方法在岩土工程中得到重视[1−2]。
杨上清等[5]运用ANSYS软件并结合JC法对某一高土石坝边坡进行时程分析,通过迭代计算得到可靠度指标,求得动力可靠度安全系数及最小可靠度指标;罗丽娟等[6]在深入分析可靠度指标的几何意义和JC法的基本原理的基础上,构造了滑坡抗滑桩结构的功能函数,建立了基于ANSYS软件和JC法的抗滑桩结构可靠度计算模型,并研制了相应算法;左熹等[7]基于JC法提出了地下结构的动力可靠性分析方法,建立地基土-地铁隧道非线性动力相互作用的有限元分析模型,将地基土-地铁隧道结构体系视为平面应变问题,采用Davidenkov动力本构模型和动塑性损伤模型,分析在地震动作用下地铁隧道结构的应力特性,进一步研究其动力可靠性,得到隧道结构的可靠度和可靠指标,以此评价地铁隧道结构的可靠性;黄灵芝等[8]基于JC法建立了重力坝深层抗滑稳定可靠度分析模型,以刚体极限平衡法构造了重力坝双斜滑动面深层抗滑稳定极限状态函数,以滑裂面抗剪断摩擦系数和抗剪断凝聚力为随机变量,分析重力坝双斜滑动面深层抗滑稳定安全度;胡平安等[9]运用JC法并结合实例对尾矿坝进行稳定性分析,分别求出了尾矿坝在正常和洪水工况下运行时的可靠度指标,发现可靠度指标对坝体材料物理力学参数变异性的敏感度高于安全系数,因而得出可靠度方法可以更加全面、客观地反映出尾矿坝稳定性真实状态的结论;朱唤珍等[10]针对一次二阶矩法计算复杂、高度非线性功能函数的可靠指标时,求解功能函数对随机变量的偏导数极其困难的问题提出用响应面函数代替原功能函数的方法,用响应面法分析强度准则参数分布类型和岩体参数之间的相关性对三维Hoek-Brown准则可靠度的影响规律。
随着各种方法的相互融合和交叉使用,各种计算方式的灵活交织,使用先进的计算技术,可靠度分析方法的使用更为广泛,计算效率更高。本文主要依托某土坡滑裂面通过MATLAB软件分别对JC法和映射变换法进行计算,获得滑裂面的可靠度并进行比较分析。
1 可靠度原理
1.1 独立正态分布
针对独立正态分布随机变量,设结构的极限状态方程为:

1.2 JC法
JC法是采用当量正态化的验算方法,是国际安全度联合委员会(JCSS)推荐使用的方法,所以称为JC法,又称当量正态化法。
设X中的Xi为正态分布变量,其均值为μxi,标准差为σxi,概率密度函数为fxi(xi),累积分布函数Fxi(xi)。与Xi相应的当量正态化变量为满足正态分布),其均值为标准差为概率密度函数为累积分布函数为根据当量正态化条件要求,在验算点和Xi的累积分布函数和概率密度函数分别对应相等,如图1所示。


图1 JC法的当量正态化条件
根据式(10)和式(11)可以得到当量正态化变量的均值和标准差,

对于如对数正态分布、Weibull分布、极值I型分布等常用的分布类型,均可由式(12)和(13)得到所需的正态变量的均值和方差。在数值计算中,并不需要针对其具体分布推导出均值和标准差的表达式。
参照独立正态分布变量的验算点法的迭代步骤,在迭代中增加了非正态变量的正态变化过程就可以建立JC法的迭代计算步骤。JC法的迭代计算步骤如下:

1.3 映射变换法
映射变量法,又称为全分布变换法,其原理是利用累积分布函数值相加的映射,将非正态分布随机变量变换为正态分布随机变量。
假设基本随机变量向量X=(X1,X2,……,Xn)中的各个分量均为独立非正态分布变量,Xi(i=1,2,3,……,n)的概率密度函数为fxi(xi),累积分布函数为Fxi(xi)。对每个变量Xi,作下列变换以将任意随机变量向量X映射成标准正态变量向量Y:
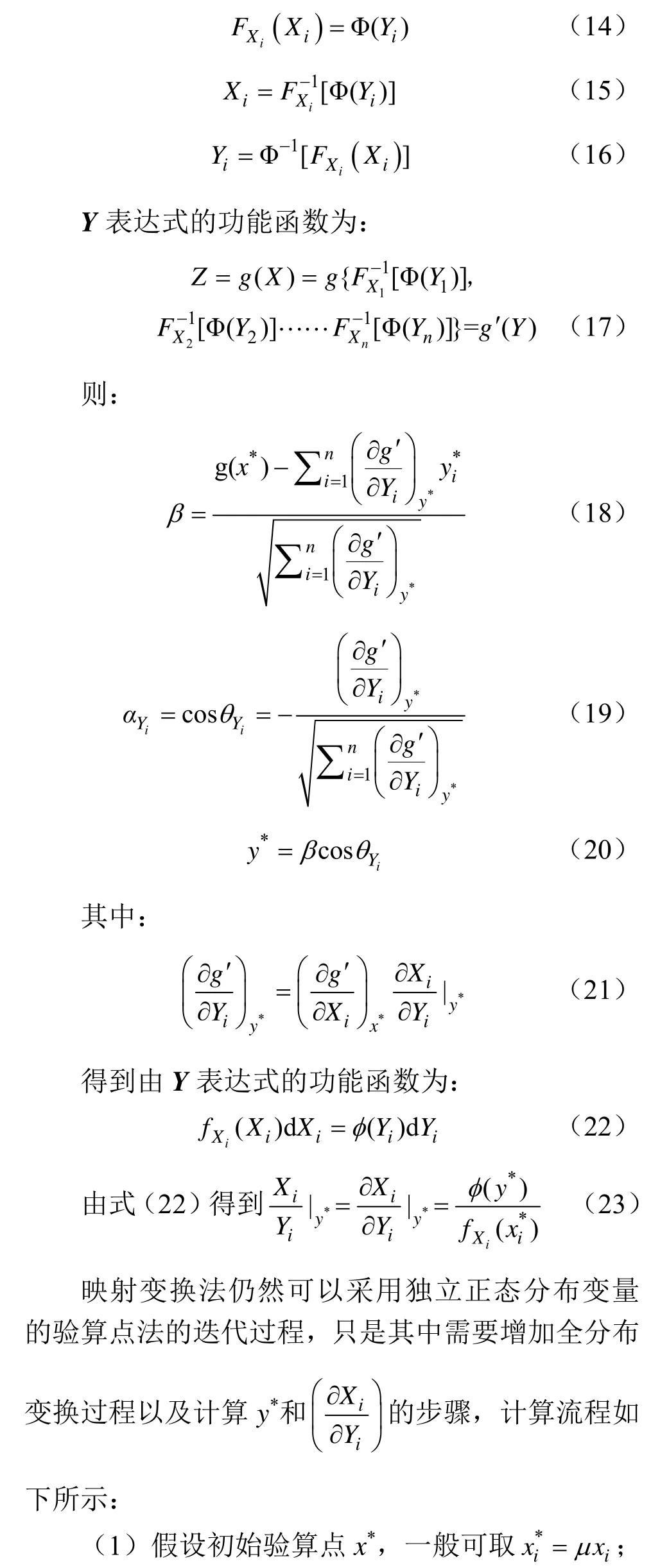
(2)根据x*,利用式(16)计算y*的初始值;
(3)利用式(19)、式(21)和式(23)计算cosθYi;
(4)利用式(18)、式(21)和式(23)计算计算β;
(5)利用式(20)计算y*;
(6)利用式(15)计算计算x*
(7)以新的xi*,重复步骤(3)至(6),直至前后两次‖x*‖之差小于ε。
2 模拟实例
如图2所示,土体沿圆弧滑裂面绕O点发生滑动破坏,W为滑动土体的自重,坡内土层分为两层,F1,F2分别为第一层土和第二层土提供的抗滑阻力,T为荷载。对土坡滑动破坏问题定义安全系数为:
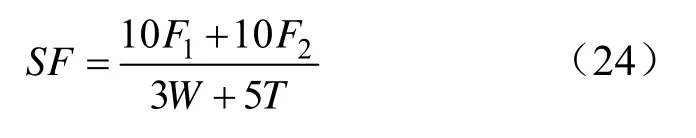
安全系数小于1时,土坡发生滑动破坏。则功能函数可表示为:


图2 土坡抗滑稳定分析
随机变量服从独立正态分布,其均值和变异系数见表1。

表1 基本随机变量统计值
3 计算结果
实例中,假设F1,F2服从对数正态分布,W服从正态分布,T服从极值I型分布(极大值),均值和标准差不变。
首先根据均值和标准差计算非正态分布的参数。



表2 JC法迭代计算结果
得到可靠度指标β=2.371;验算点坐标F1=65.65,F2=132.27,W=643.44,T=9.80。
按照流程,采用映射变量法迭代计算,结果见表3。

表3 映射变量法迭代计算结果
得到可靠度指标β=2.3706;验算点坐标F1=65.67,F2=132.25,W=643.41,T=9.80。
从两种方法的计算结果中可以看出,JC法和映射变量法计算结果完全吻合,计算精度满足要求,且数据较为合理。
4 结论
通过对比分析得出,在岩土工程中可靠性分析是一种有效的设计和评价的手段。本文针对某土坡的滑裂面进行可靠度计算分析,通过MATLAB软件分别用JC法和映射变换法进行计算,比较分析可知,两种方法的计算结果的差比较小,能够反映出可靠度分析的合理性,可为岩土工程中可靠度的分析提供参考。JC法和映射变换法,计算方法简单明了,计算精度高,此类方法可以在岩土工程中得到越来越广泛地运用。
