海水声速剖面约束下的速度分析方法
2021-06-06高子傲孙建国
高子傲,孙建国
吉林大学 地球探测科学与技术学院,长春 130026
0 引言
海水速度是非常重要的参数,对反演和成像均有影响。Munk于1947年提出了深海声道模型的数学表达式。Brandt在1975年首次指出声波成像研究海洋水体运动和精细结构的可能性[1]。Phillips et al.对浅滩地震资料的研究中发现利用地震反射波可以反映海水的温盐结构[2]。Holbrook et al.在对芬兰某地地震剖面资料处理时发现了海水层细结构,推断可以利用反射地震研究海洋水体运动[3]。Biescas et al.在重处理Iberian--Atlantic Margin项目的海洋地震反射剖面时,发现了得到海洋学验证的涡旋结构,证实可利用反射地震方法研究海洋水体运动[4]。宋海斌等[5]、宋洋等[6]和黄兴辉等[7]利用海洋地震数据反演海水的温盐结构,最终得到的海水速度变化趋势与Munk给出的声速剖面曲线基本一致,为深海声道的模拟提供理论依据。鲁统祥等[8]提出了海水地震数据水层弱信号保护技术,通过有效分离水层反射信号达到保真效果。孙建国[9]通过Munk公式和海底反射走时反演,提出计算深海水体速度的理论方法。其与常规走时反演相比,利用Munk公式进行的海底反射走时反演最多只需要反演4个参数,并可利用交替反演将四参数反演化为单参数反演,大大地减少了走时反演的计算量。应用地震学方法研究深海水体反射有着重要的意义。
目前,将反射地震方法引入海洋学研究逐步深化。但在利用AVO技术研究海水物性差异方面,针对水体反射地震数据的处理研究鲜少,尤其是反演水体速度的方法研究鲜少。与海底岩性变化相比,水体的速度变化不大,这导致水层反射信号弱化。在采集的海洋反射数据中,水层反射信号常与背景噪声信号产生混叠,无法计算获得准确的海水速度信息。
本文提出计算声速剖面叠加速度,即水层叠加速度的新方法。应用Munk公式对海水声速剖面进行建模,计算拟合海水层条件下的射线路径、走时[10--12]。将声速剖面正演地震记录处理后进行速度分析[13--14],即通过识别并补偿阈值化处理后的声速剖面地震记录,使间断的同相轴及其幅值得到恢复,强化水层反射信号,实现对水体的有效速度分析,得到水层的叠加速度。将此方法应用到海洋地震资料中,通过计算水层反射得到了真实有效的水体叠加速度值和正确的海水速度分布趋势。
1 声速剖面水体建模
声速剖面是描述深海声道现象的模型。深海声道是在一定水深产生的声波波导。在温度、压力和其他因素影响下,其声波速度随深度变化呈现具有极小值点的二次曲线形态。而此极小值点所处的深度为深海声道轴深度。
声速剖面由Munk理论公式[9]约束:
v(z)=v0{1+ε[e-η-(1-η)]}
(1)

通过Munk公式[9]描述纵向水体速度变化,建立初始速度模型,明确水体纵向速度(图1)。模型横纵网格间距为5 m,声道轴深度为1 000 m。在经典Munk声速剖面模型中,声道轴处的速度对应声速剖面极小值1 500 m/s。
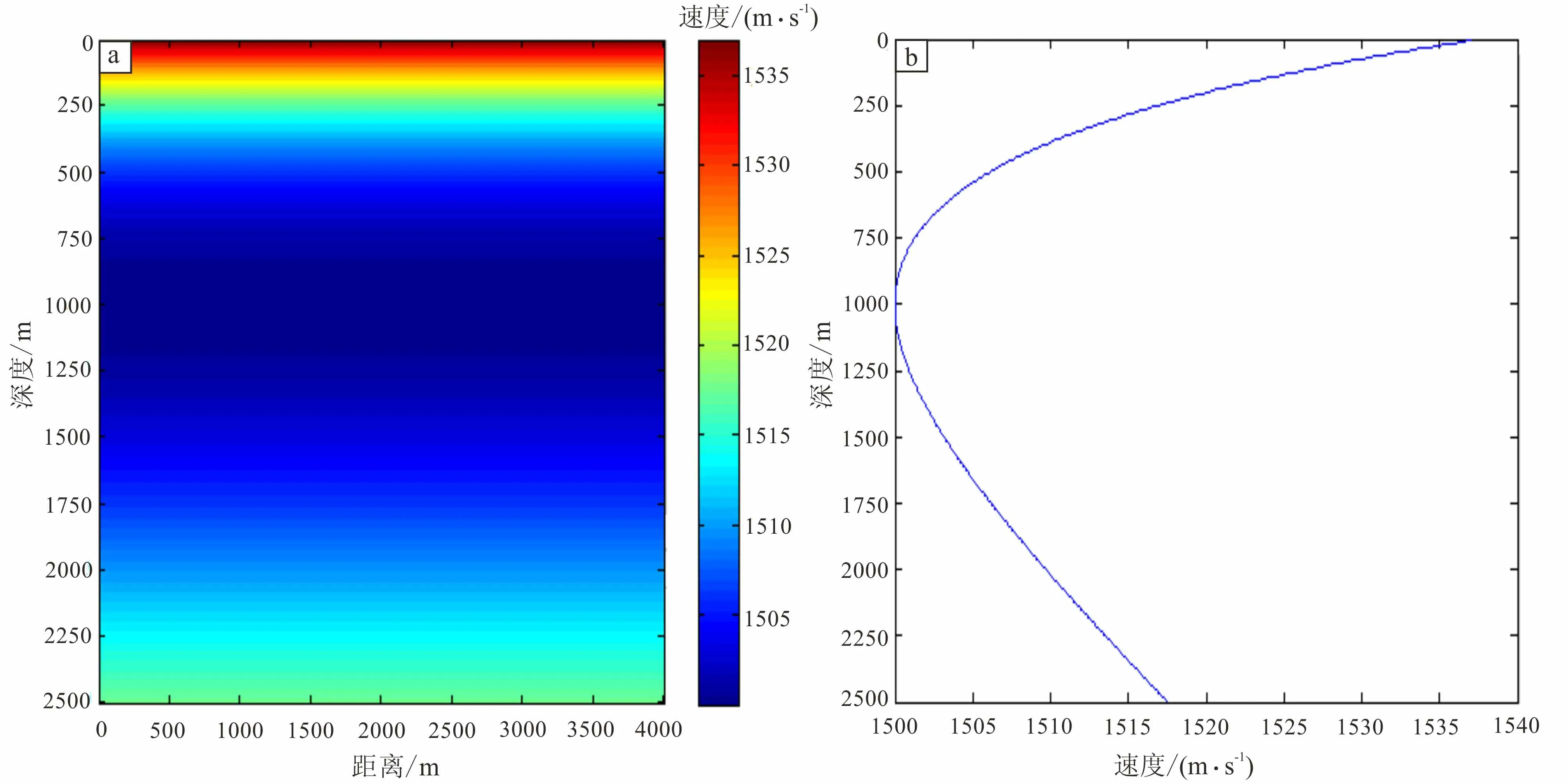
图1 Munk初始速度模型(a)和剖面速度曲线(b)Fig.1 Munk initial velocity model(a)and profile velocity curve(b)
二维运动学射线追踪系统[13]表示为:
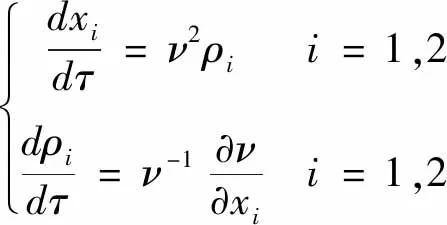
(2)
式中:xi是位置坐标分量;ρi为慢度矢量分量;v是速度矢量。求解此式为求解初值问题的常微分方程。应用四阶龙格--库塔(Runge--Kutta)公式,式(2)改写为:
(3)
式中:λ为x或z;Δτ为时间步长;Kxi,Kzi,Lxi,
Lzi为求解系数。通过式(3)可以求得网格内的射线路径。即根据震源初始值,应用龙格库塔法以固定的时间步长计算向外波前的传播,若射线间距过大,则在邻近射线间插入新射线。同时,对射线网格内结点的参数进行计算。初始震源为中心坐标为(500,0),半径为1 m的半圆。取角度间隔为1.5°,即对0~180°范围内共120条射线以步长2 000进行追踪计算。震源子波采用主频为25 Hz的雷克子波。图2为对经典Munk模型应用波前构筑法计算得到的模型走时及模型内射线路径。其中,模型网格数为1 000×1 000,横纵网格间距为5 m。模型最大速度vmax=1 537 m/s,最小速度vmin=1 500 m/s。时间步长为0.004 s。射线理论要求地震波一个波长范围内满足介质相对光滑条件,经典Munk模型满足此条件。
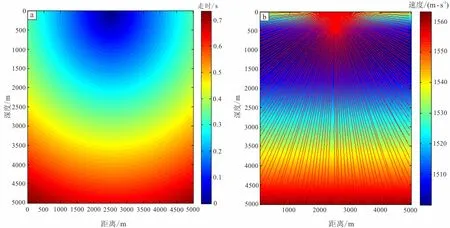
图2 Munk模型走时(a)及射线路径计算(b)Fig.2 Munk model travel time(a) and ray path(b)
采用八阶声波方程有限差分方法对经典Munk声速剖面模型进行数值模拟,边界条件采用PML吸收边界条件。图3为声速剖面有限差分正演。其中,声速剖面速度模型的横纵网格数为800×500,网格间距为5。正演的震源坐标为(400,10),时间采样点为1 300,时间步长为0.002 5 s。震源采用雷克子波,主频为30 Hz。道间距为5 m。最小炮检距5 m,最大炮检距2 000 m。图3a为正演结果。图3b为不同尺度细节放大的部分经典Munk模型地震记录。相较于强直达波与底层反射信号,水层反射信号极其微弱。经过正演得到声速剖面多炮反射地震数据后,观察直达波与底层反射形态,用函数切割法切除直达波等浅层干扰信息及地层强反射信息,进行阈值化处理,清除与速度分析计算无关的微弱的值,得到仅有水层反射部分的地震记录(图4)。图4a对应图3a中单边放炮切除直达波与底层反射波后的结果。
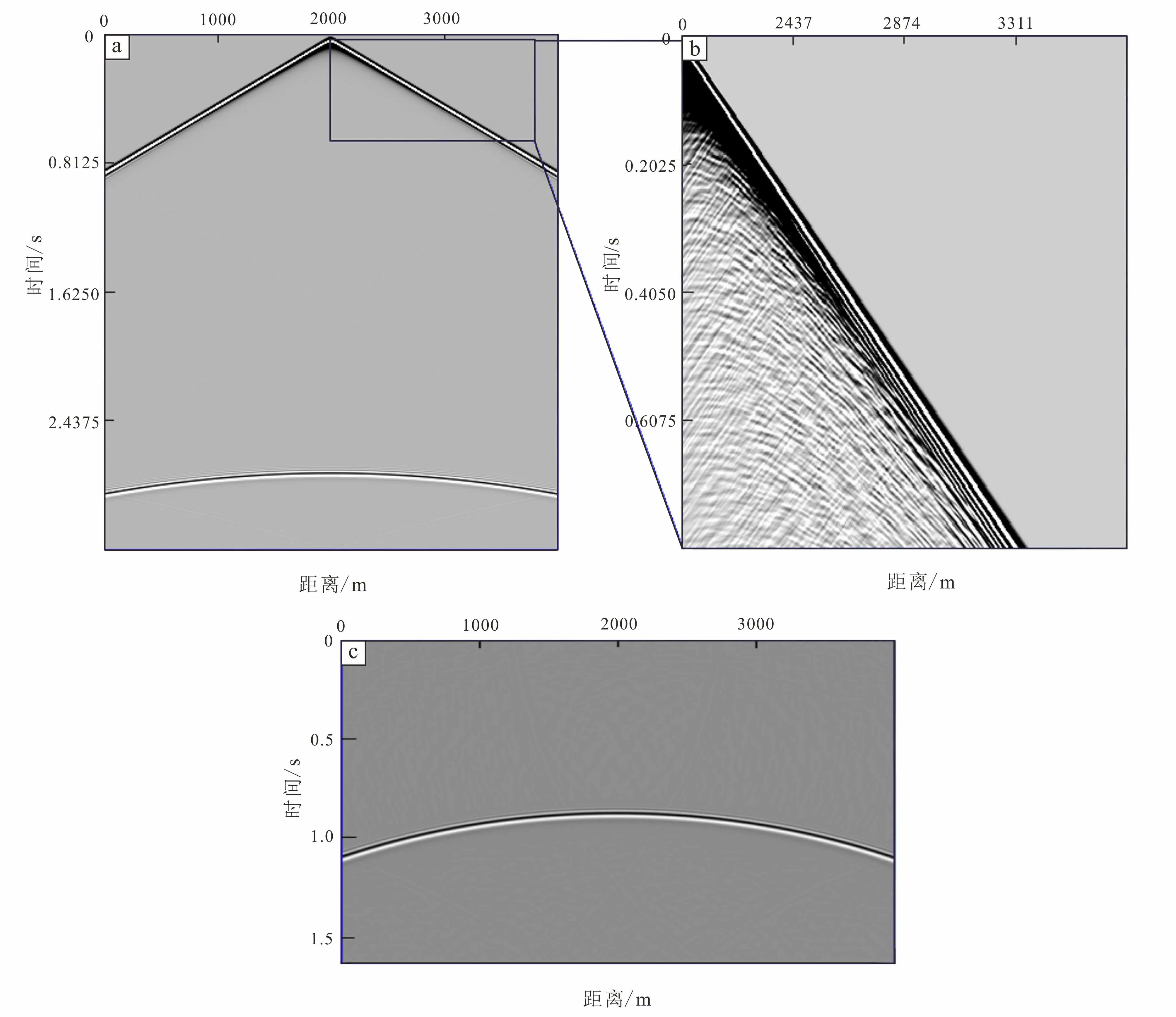
图3 Munk模型地震记录(a),Munk模型地震记录细节放大(b)和2.5 s波场快照(c)Fig.3 Munk model seismic record(a), zoom in details of munk model seismic record(b)and 2.5 s wave field snapshot(c)

图4 原始声速剖面地震记录(a)和阈值化处理后的结果(b)Fig.4 Seismic record of initial sound velocity profile(a)and thresholding result(b)
阈值化原则为,选择数据中明显低于有效数值两个数量级的某一数值作为阈值,将数据中大于该阈值的值保持原状,将小于该阈值的值变为0。具体表示为:
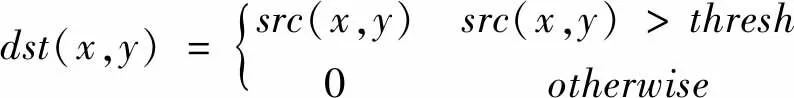
(4)
式中:dst(x,y)为阈值化处理后的结果。src(x,y)为原始数据结果。
由于声速剖面速度光滑梯度变化,使得水层反射同相轴能量微弱并出现同相轴间断现象(图5)。
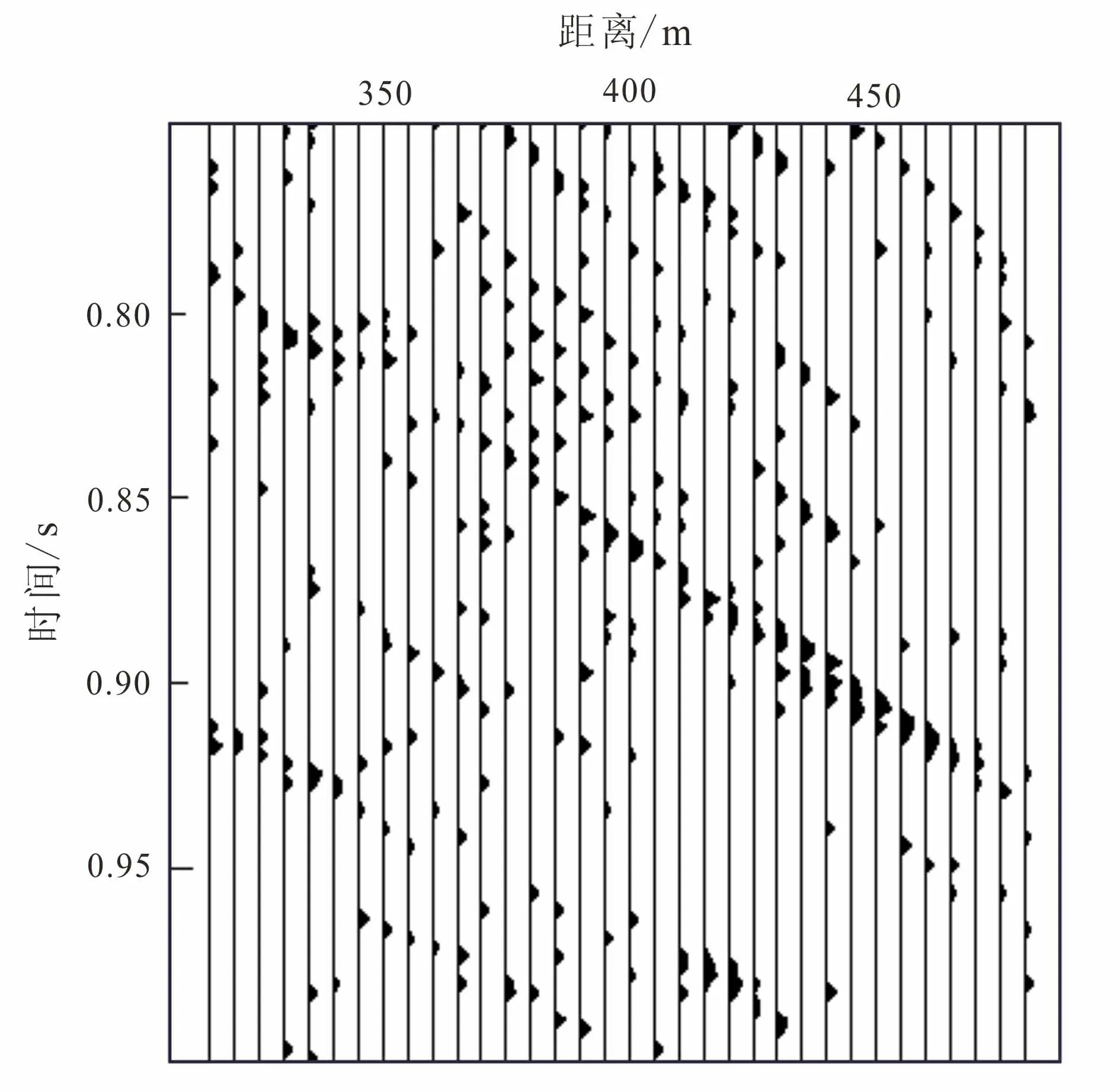
图5 水层反射地震记录同相轴间断Fig.5 Discontinuity in phase axis of water reflection seismic record
2 声速剖面速度分析方法
为增强水层反射地震记录中的有效信号,对阈值化处理的声速剖面地震记录进行同相轴信息补偿,消除由速度光滑梯度变化带来的同相轴弱化影响。具体是选取能直观判断正确而有效的同相轴,根据其趋势拾取同相轴坐标信息,建立高斯级数拟合公式拟合同相轴,对声速剖面反射地震记录水体反射同相轴坐标进行弱振幅补偿,并将原始数据中有效同相轴的最大数值作为拟合同相轴的数据数值。
拟合正确的标准为,拟合后的速度分析结果与拟合前的趋势一致。这是补偿方法实施的唯一原则。高斯级数拟合形式为:
(5)
式中:a1,a2,b1,b2,c1,c2为拟合系数。
高斯函数表示为:
(6)
高斯函数描述的对称谱图像可表示为图6。其中,a1,b1,c1分别为峰高、峰位和区域宽度,其中c1=2·d2。为了得到拟合系数,需将高斯函数进行转换以符合多项式结构。将式(6)改写为:
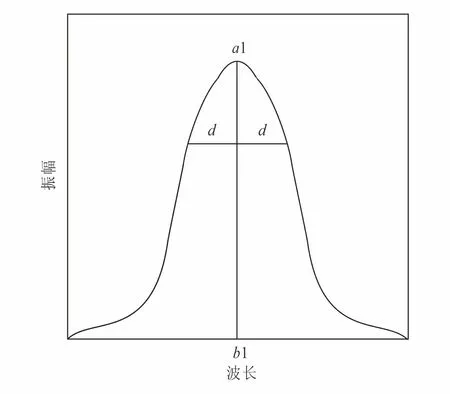
图6 对称谱图像Fig.6 Symmetrical spectral image
(7)
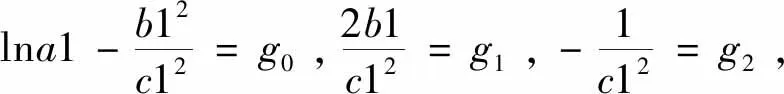
(8)
矩阵表示形式为:
(9)
根据拾取的坐标矩阵,通过求解系数矩阵得到拟合系数g0,g1,g2,从而得到所需要的a1,b1,c1。拟合精确度以决定系数(coefficient of determination)判定,定义为:
(10)
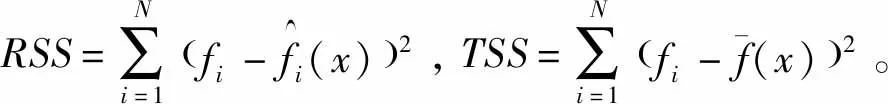
由于同相轴拟合是基于原有同相轴坐标拾取,对精度要求严格,必须遵守拟合后的速度分析结果与拟合前的趋势一致的原则。在拟合补偿同相轴后的数据中添加阈值化消除掉的值,得到还原真实地震记录的同相轴补偿水体地震记录。图7表示将水层反射地震记录实施同相轴补偿。其中,编号1~4表示相应的水层反射得到补偿后的同相轴。
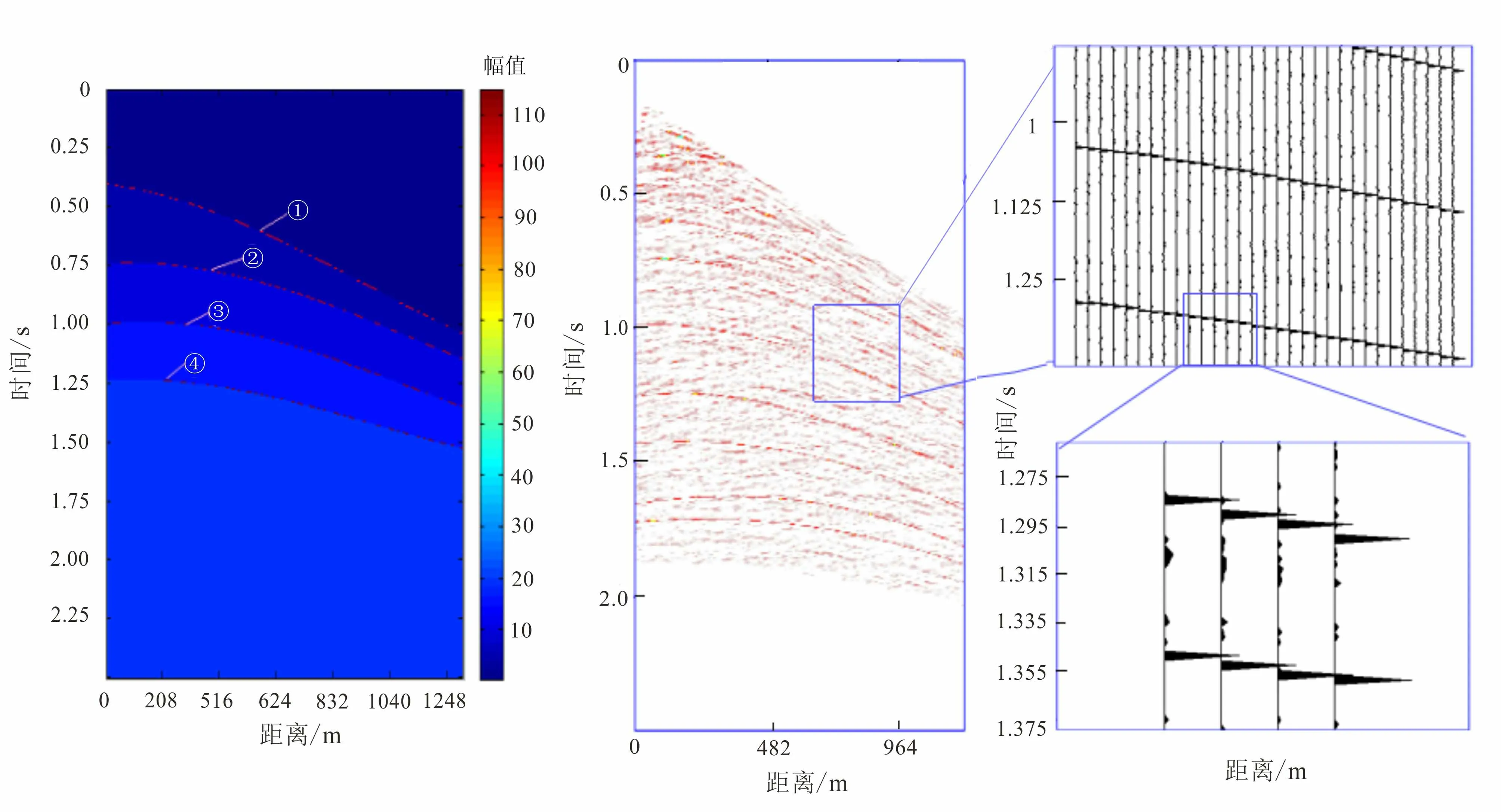
图7 同相轴补偿Fig.7 Events compensation
抽取共中心点道集并进行叠加速度谱计算。在采用的速度分析方法里,归一化互相关和方法通过求取每个地震道内的归一化的离散值,得到归一化互相关和K。K达到最大时的速度即为所求的叠加速度。归一化互相关和[15]由下式定义:
(11)
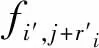
对声速剖面共中心点道集地震记录和经过同相轴补偿处理后的声速剖面地震记录分别进行叠加速度谱计算(图8、9)。
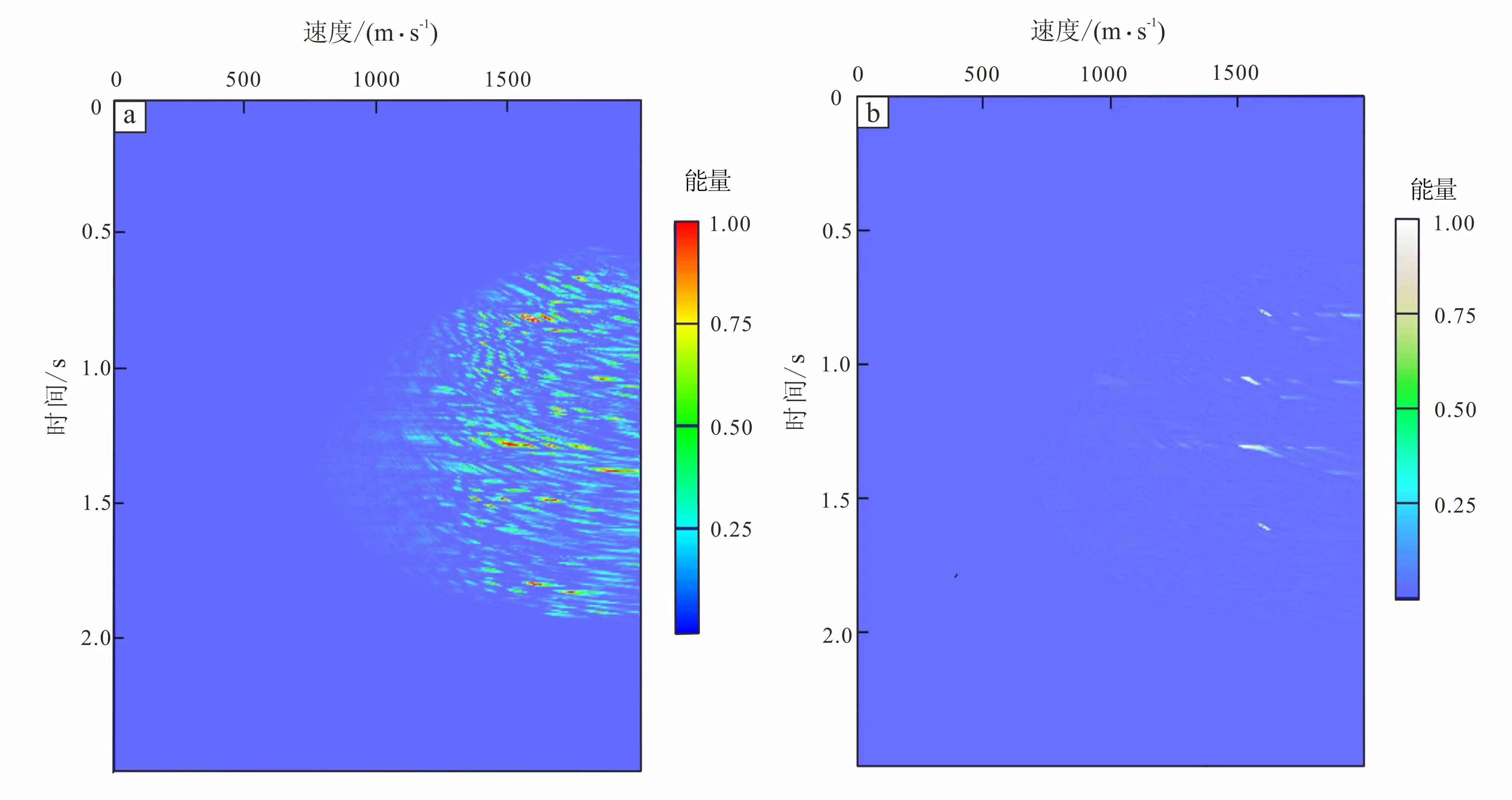
a.经典声速剖面速度谱;b.用归一化选择性互相关和方法对同相轴补偿后的速度谱。图8 速度谱计算结果Fig.8 Velocity spectrum calculation results
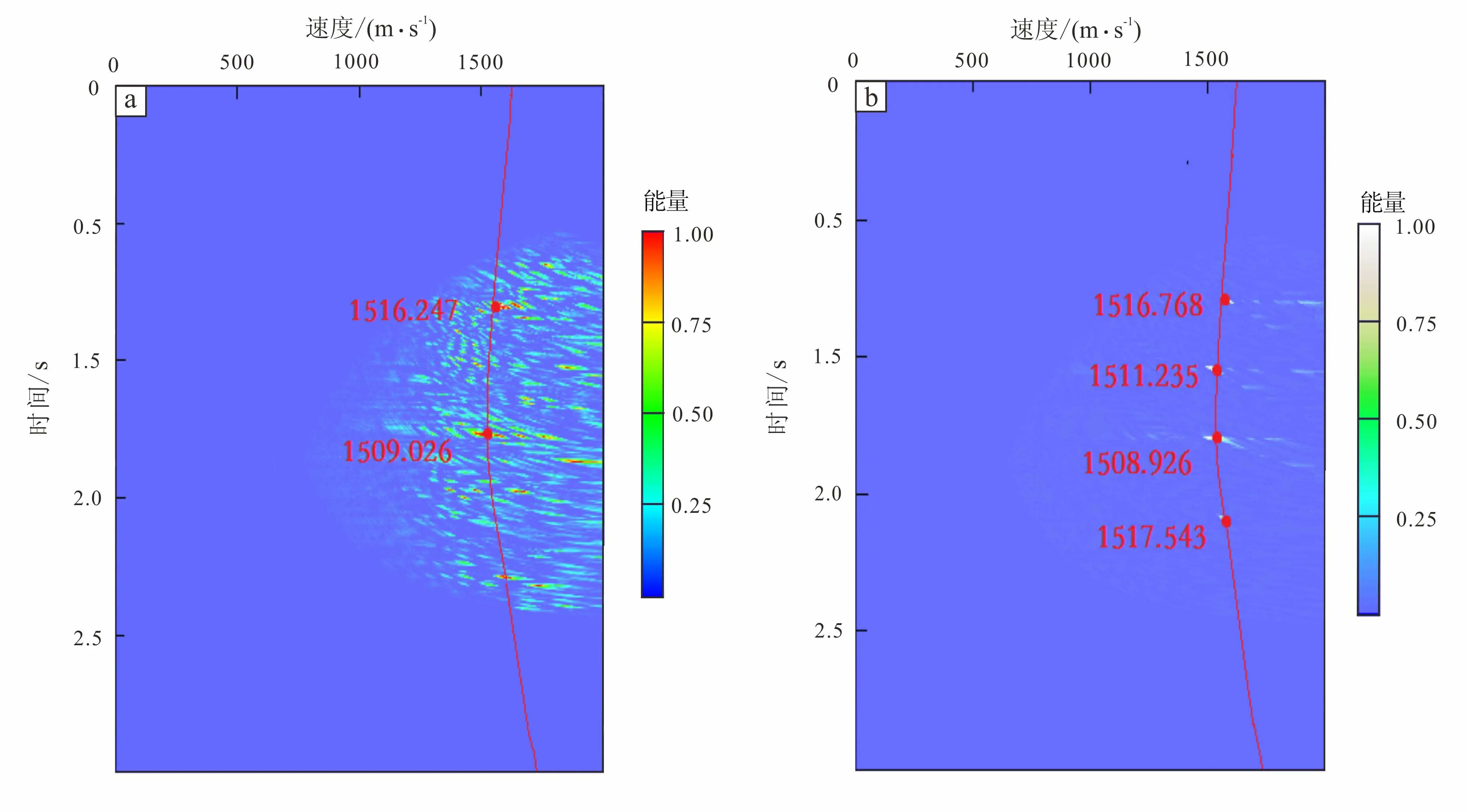
a.声速剖面速度分析结果;b.归一化选择性互相关和方法对同相轴补偿后的速度分析结果。图9 速度分析结果Fig.9 Velocity analysis results
Munk声速剖面的速度谱中,有数量较少的有效速度团。速度团能量分散,不容易分辨。在有效的速度团中,可以得到声速剖面声道轴处的叠加速度值,对应海水速度分布的最小值。通过计算可验证速度分析结果与补偿方法的正确性。
地下为均匀介质,双程旅行时时距曲线方程[15]为:
(12)
式中:介质速度为v;t0为零炮检距双程旅行时间。根据速度谱计算原理,走时接近零炮检距双程旅行时间时的速度团能量最大。
当共中心点道集第一道的炮检距为零炮检距时,将声速剖面进行微元化,零炮检距双程走时T的表达式为:

(13)
引入Munk公式表示为:
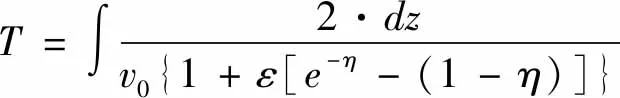
(14)
将Munk声速剖面经典参数代入,得到:
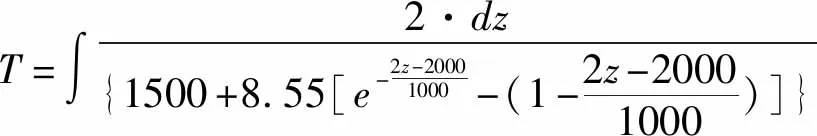
(15)
计算式(15)积分方程,得到不同深度下双程走时T的数值解。零炮检距双程走时T与深度的具体关系为:
理论模型速度分析计算所用的共中心点道集首道炮检距接近零炮检距,在大尺度的一定误差范围内,可根据表1判断声道轴处速度团的拾取是否正确。
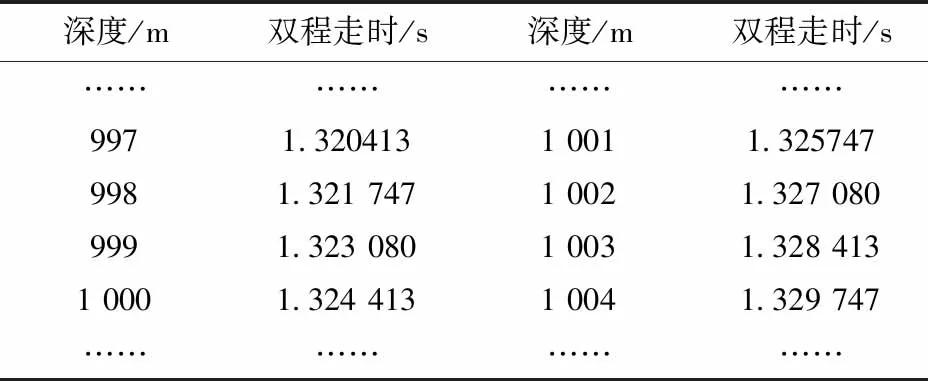
表1 深度及对应走时对照表Table 1 Depth and corresponding travel time comparison table
根据表1,利用速度分析拾取的声道轴处的双程走时T可以得到该处对应的确切深度。按照声速剖面速度公式,利用深度信息可以计算声速剖面声道轴处的速度。
Munk声速剖面模型的正演时间间隔为2.5 ms,理论模型速度谱拾取的声道轴双程走时--叠加速度坐标为(531.453,1 509.026)。应用同相轴补偿方法后的速度谱拾取坐标为(530.246,1 508.926)。计算得到双程旅行时间为1.328 632 5 s及1.325 615 s。根据表1所示时深关系,声道轴的计算位置为1 001~1 003 m。考虑首道共中心点道集的炮检距并非零炮检距的计算误差,计算结果与实际声道轴深度1 000 m的位置十分接近。
Munk经典声速剖面模型地震记录与应用同相轴补偿方法计算的地震记录经过速度分析得到了分布一致的叠加速度。声道轴处的均方根速度值均为1 510±。这证明了同相轴补偿方法的有效性。
3 实际海水数据速度分析
对于实际海水反射地震记录数据,以美国东海岸实测数据为例。1978年,美国地质调查局(USGS)与地球物理服务公司(GSI)合作采集总长为4 813 km的反射地震数据。在美国东海岸共采集38条地震剖面。实际数据采用与海岸线基本平行的第38号测线。对多炮地震数据抽取共中心点道集,切除初至波及海底反射,保留水层部分记录。水层部分地震记录时间采样点为750,时间采样间隔为4 ms。通过对此共中心点道集数据应用相似系数法、归一化互相关和法及归一化选择性互相关和法进行速度分析,得到如图10b、图11a、图11b所示结果。
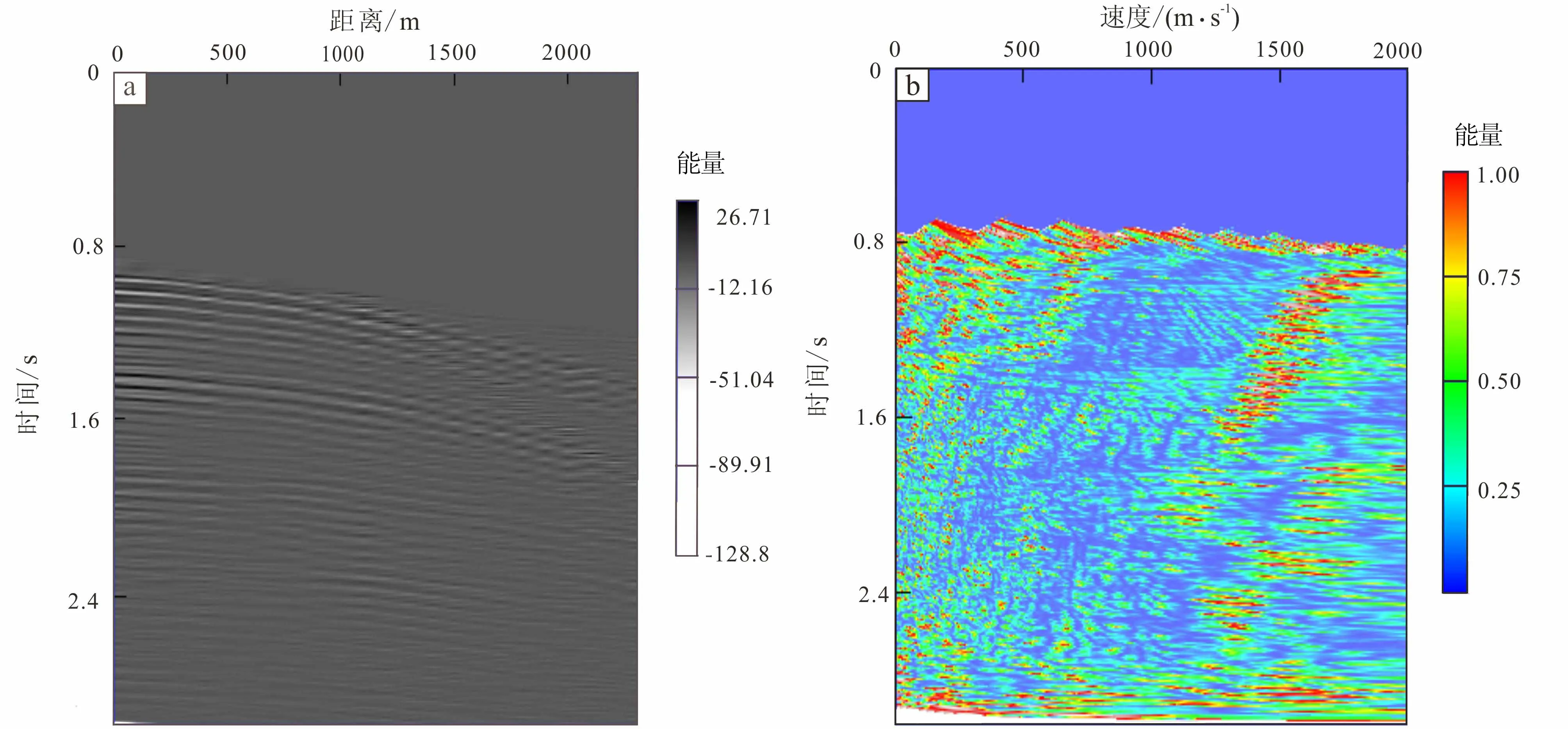
图10 真实水层反射数据(a)和利用相似系数法计算水层反射速度谱(b)Fig.10 Real water layer reflection data(a) and calculation of water layer reflection velocity spectrums using similarity coefficient method(b)
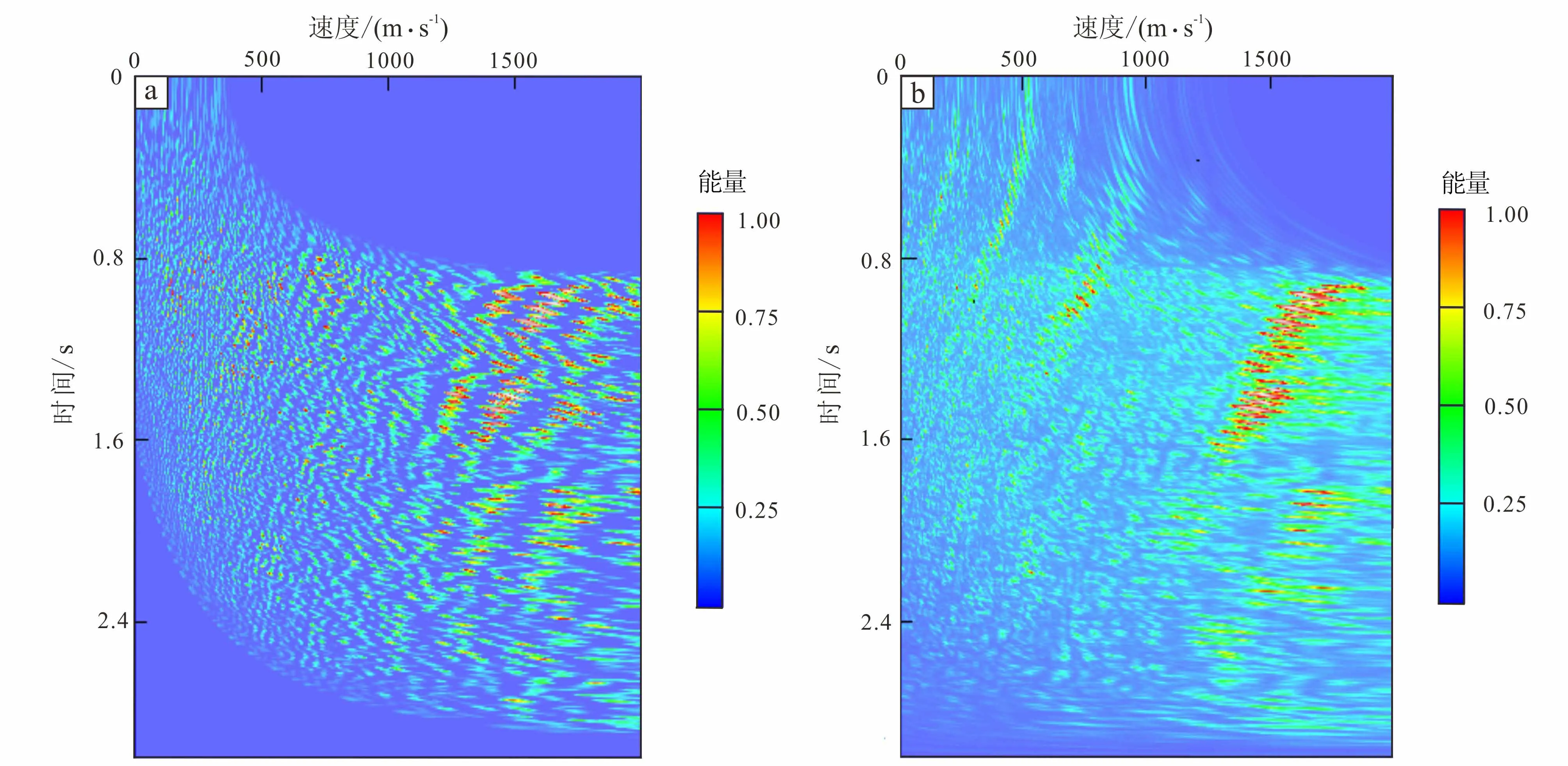
图11 归一化选择性互相关和方法计算速度谱(a)和归一化互相关和方法计算速度谱(b)Fig.11 Calculation of stacking velocity panel using normalized Cross--Correlation Sum method(a) and calculition of stacking velocity panel using normalized selective Cross--Correlation Sum method(b)
海水速度在大范围内分布在1 500 m/s±。原始数据计算的速度谱中,仅能得出一部分有效速度。由于背景噪声影响,速度谱中出现大量假能量团,无法得到准确的叠加速度数值及完整的海水叠加速度分布趋势。
应用同相轴补偿方法,将原始地震记录同相轴校正并增强幅值。计算并得到最终的速度分析结果。阈值化后同相轴补偿前后的数据结果如图12a、图12b所示。在对应用同相轴补偿方法后的数据进行相似系数法和归一化选择性互相关和法得到的速度分析结果如图13a、图13b所示。
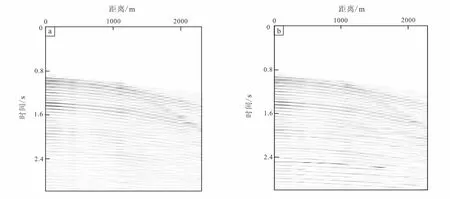
图12 阈值化后的真实水层反射数据(a)和同相轴补偿后的结果(b)Fig.12 Real water layer reflection data after thresholding(a)and result after events compensation(b)
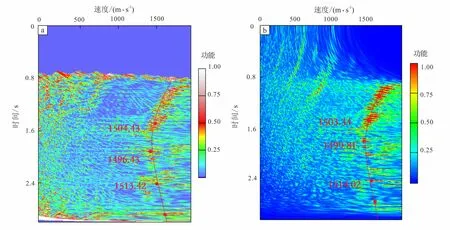
图13 相似系数法速度分析结果(a)和归一化互相关和法速度分析结果(b)Fig.13 Velocity analysis results of similarity coefficient method(a)and velocity analysis results of normalized Cross--Correlation Sum method(b)
通过对初始水层反射地震记录有效反射同相轴的识别与加强,削弱了由于背景噪声所造成的海水层反射同相轴间断、错位。经过速度分析后得到准确的海水层叠加速度值及海水叠加速度分布趋势。这提供了更加真实、有效的水层叠加速度计算结果。
4 结论
(1)本文在应用Munk公式进行声速剖面水体建模的前提下,经过正演得到声速剖面地震记录后,应用同相轴补偿方法,使得可以对速度光滑梯度变化的声速剖面进行有效速度分析。提高了海洋地震资料的分辨率,为水体反射速度分析提供方法。
(2)通过将水体反射同相轴校正及能量补偿方法应用到实际海洋地震数据,得到了更为真实准确的海水叠加速度值及叠加速度分布趋势,证实此方法应用于实际生产中的有效性,为进一步获取水层速度提供了新的手段。
