地震液化侧移计算方法对比

杨彦鑫, 蒙国往, 黄 翔, 王蒙婷, 马建林

(1.桂林电子科技大学 建筑与交通工程学院，广西 桂林 541004； 2.西南交通大学 土木工程学院, 成都 610031;3.广西大学 土木建筑工程学院, 南宁 530004; 4.桂林理工大学 土木与建筑工程学院, 广西 桂林 541004)

地震液化引起的地面侧移(lateral spreading)是常见的破坏现象。侧移是指在地震中饱和砂土发生液化, 使地表覆土沿缓坡滑动面或者朝着自由面产生移动的现象。侧移的计算方法分为经验公式法、数值计算法、简化计算法和模型试验法。文献[1-5]根据液化场地的几何参数和地震特征提出经验公式, 但未考虑侧移的实际产生机理和场地动力响应。数值计算方法[6-12]根据不同砂土液化本构模型计算侧移, 如边界面模型、多面模型和广义塑性模型等，可模拟土体的非线性变形和孔压变化及砂土液化后模型[13], 因此被广泛应用。简化计算法[14]是指根据Newmark滑块法及改进后的Newmark滑块法[15-17]计算侧移。模型试验法[18-19]根据大型振动台或离心机模型试验预测侧移, 室内试验可研究侧移产生的机理和影响因素, 但受试验条件限制。数学模型法[20]则根据相关数学模型对砂土液化或液化侧移值进行预测分析。由于各侧移计算方法的适用性不同, 因此有必要对不同的侧移计算方法进行评估并充分考虑地震和场地特征, 提出简单实用的侧移计算方法。本文利用简化计算法和数值计算对美国WLA(Wildlife Array)液化侧移进行分析, 选用场地土体参数和场地记录地震波, 计算对比不同的侧移值, 对现有侧移计算方法进行评估。考虑侧移场地的液化特性, 基于Newmark滑块法和场地液化时间, 计算WLA场地的侧移并验证该方法的适用性。

1 WLA(Wildlife Array)场地

WLA液化台阵(wildlife site array)由美国地质调查局建立[21], 位于美国加利福尼亚州南部的阿拉莫河冲积平原上。该液化台阵记录了1987年Superstition Hills地震时液化土层下的加速度时程曲线和不同位置的孔压曲线。在地震中粉质砂土层发生液化, 图1所示为WLA液化台阵地质剖面图, 由上至下分别为粉土、粉质砂土、粉质黏土和粉土, 其中粉土层厚2.5 m, 粉质砂土层厚3.7 m,粉质黏土层厚4.8 m, 粉土层位于粉质黏土以下。WLA液化台阵埋设P1～P6共6个孔压传感器, 设置2个强震记录仪, 其中SM1位于台阵表面, SM2位于粉质黏土层中。表1为场地的土体参数, 为区分不同性质的粉质砂土, 将粉土下地下水位上1 m厚的粉质砂土记为粉质砂土-1, 将地下水位以下粉质砂土记为粉质砂土-2。1987年Supersitition Hills地震中, 该场地朝阿拉莫河方向发生了0.18 m的侧移。

图1 WLA液化台阵剖面图[22]Fig.1 Profile of WLA liquefaction array

表1 WLA液化台阵土层参数Table 1 Parameters of WLA liquefaction array

2 液化侧移对比计算分析

对WLA场地计算分析, 选取Newmark滑块法、有限差分法对该场地进行计算验证。选用FLAC2D[23]建模, 设置土体参数和边界条件, 并输入地震波, 其中在FLAC2D中分别采用PM4Sand[24]和Finn[6,25]砂土液化模型模拟液化土。

2.1 动荷载输入

将WLA场地液化土下的强震记录(IVW-090)作为地震加速度输入, 取自PEER[26]的数据库, 其加速度峰值a=0.15g。图2为已进行滤波和基线调整后的地震加速度输入。对场地反卷积运算获得Newmark滑块法的地震加速度输入(IVW-090-2), 如图3所示。

图2 动荷载输入(IVW-090)Fig.2 Seismic input waves(IVW-090)

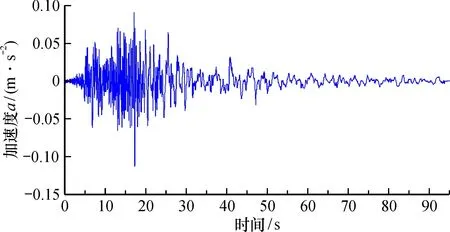
图3 地表地震波(IVW-090-2)Fig.3 Surface seismic waves(IVW-090-2)

2.2 Newmark 滑块法计算

Newmark 滑块法(Newmark sliding block method)由Newmark在1965年提出, 主要用于计算地震作用下大坝的永久位移, 后被应用于计算边坡、路基的地震永久位移。图4为Newmark 滑块示意图。

图4 Newmark 滑块法示意图Fig.4 Schematic diagram of Newmark sliding block method

Newmark 滑块法的基本假设是: 土体为刚体滑块, 在地震的作用下, 当地震加速度大于滑块的屈服加速度时, 滑块开始沿着滑动面滑动, 对地震波超过屈服加速度的部分进行二次积分, 得到动力永久位移。Newmark滑块法计算侧移的核心是根据液化土的残余抗剪强度确定屈服加速度。根据液化土的标准砂贯入度和液化土的上覆有效应力, 由液化土残余强度公式[27]计算得到液化土的残余强度

(1)

(2)

式中:(N1)60-cs是可液化土的等效纯净砂标准贯入度;Su是残余剪切强度;σv0′是液化土上覆有效应力。当考虑孔隙重分布时,选择式(1)计算液化土的残余强度;反之,选择式(2)。不考虑孔隙重分布,根据液化土的标准砂贯入度(N1)60=10.3[28]可得有效上覆应力为61.7 kPa, 计算得到残余强度为6.76 kPa。WLA液化台阵场地的屈服加速度由极限平衡法确定, 如图5所示为0.03g。输入图3所示地震波, 经两次积分得到WLA液化台阵侧移值并列于表2中, Newmark滑块法计算得到的侧移值较实际值大, 为实际值的2倍。

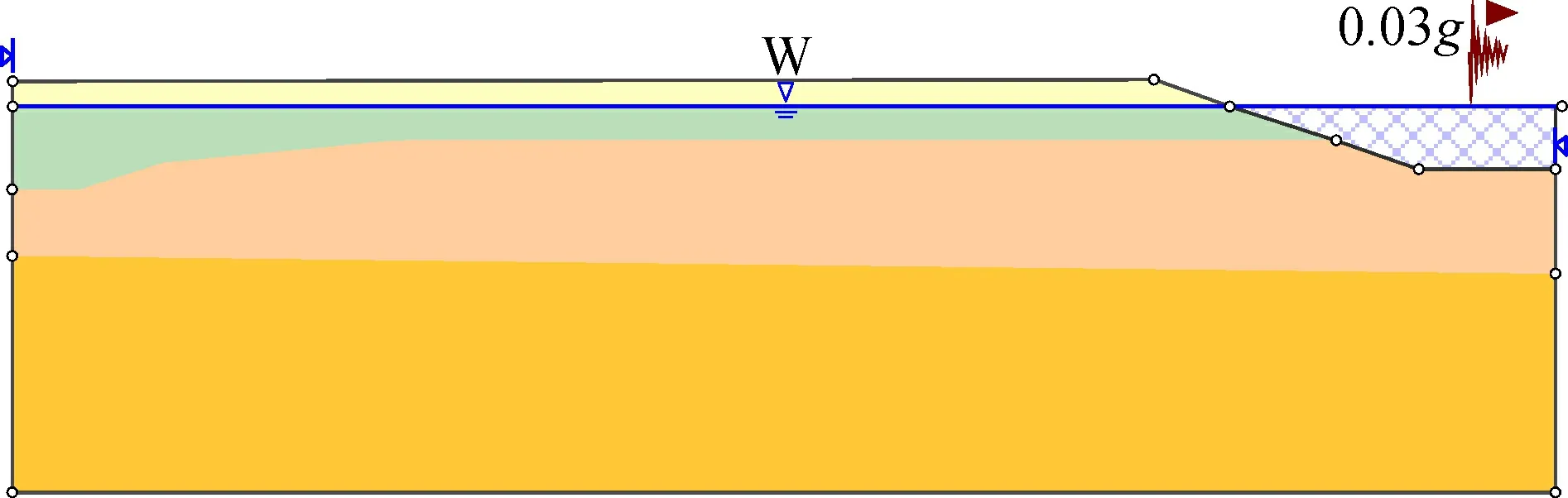
图5 屈服加速度计算Fig.5 Calculation of yield acceleration

表2 IVW-090-2地震波液化台阵侧移

2.3 基于PM4Sand本构模型的二维场地侧移计算

PM4Sand模型由Boulanger[24]提出, 在MD04[29]模型基础上发展而来。DM04塑性模型根据土体的临界状态理论和应力控制原则模拟砂土在单向荷载作用下的应力应变关系, 但不能模拟土体在动力循环荷载作用下的强度软化, PM4Sand模型改进了DM04模型在模拟土体动力响应的不足。PM4Sand模型由27个参数控制, 其中输入参数3个, 其余参数均为默认值。根据砂土的标准贯入度, 确定PM4Sand的3个主要输入参数为相对密实度Dr、剪切模量系数G和收缩率参数hp0(收缩率参数用来调整塑性模量与弹性模量比, 根据动力触探值和PM4Sand提供的校正曲线确定)。

(3)

(4)

表3给出液化土的PM4Sand取值参数, 建立数值计算模型并根据表1赋值, 如图6所示。

表3 PM4Sand模型参数Table 3 Model parameters of PM4Sand

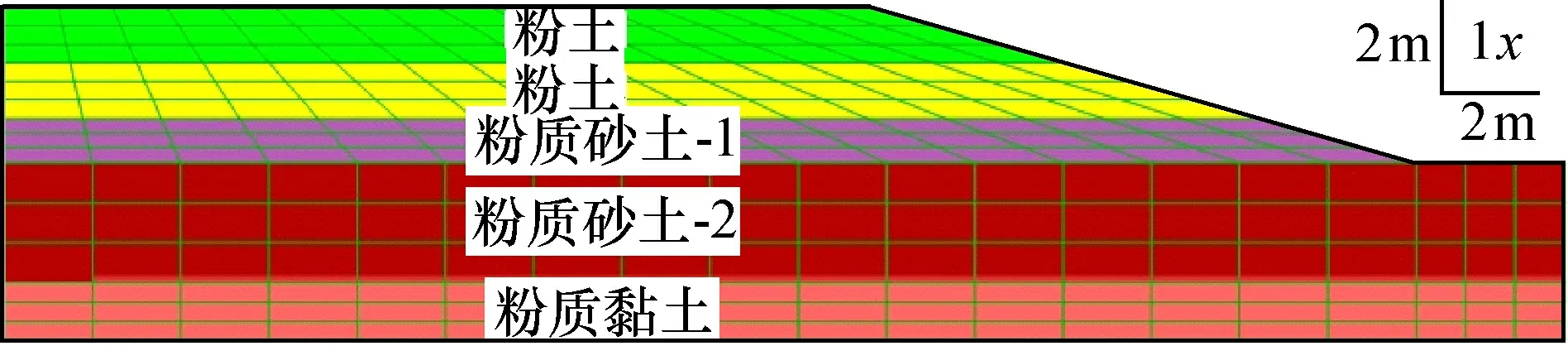
图6 动力计算模型Fig.6 Dynamic calculation model

将所有土层设置为莫尔-库伦模型生成初始应力场并设置计算模式为大变形模式。设置水位线和各层土的孔隙率、渗透率进行渗流计算并生成初始孔压, 当系统达到初始平衡后进行动力计算。将液化土设置为PM4Sand模型, 模型的边界条件为静止边界和自由场边界, 以减少边界对地震波反射, 根据Hardin模型拟合非液化土的模量衰减曲线和阻尼比曲线并设置瑞利阻尼为0.02以吸收地震输入的高频成分, 在模型底部加载地震输入。对场地自由面顶部位移记录, 当动力计算完成时, 自由端顶部位移对应为WLA的侧移。图7为场地的侧移随着时间的变化曲线, 最终场地的侧移值为70 cm, 是实测值的3.8倍。

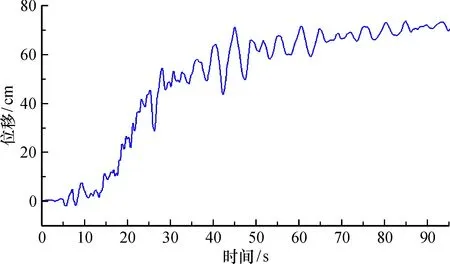
图7 PM4Sand模型场地侧移随时间变化曲线Fig.7 Curve of lateral spreading versus time with PM4Sand model

2.4 基于Finn本构模型的场地侧移计算

Finn模型能够计算在地震作用下的孔隙水压力变化, Finn模型以莫尔-库伦模型为基础计算孔隙水压力变化, 该模型认为土的塑性体积应变是土体剪应变和累计体应变的函数, 与固结压力无关, 而孔隙水压力的增加与塑性体积应变增量相关[6, 24]。孔隙水压力的变化表达为一维回弹模量与塑性体积应变的乘积

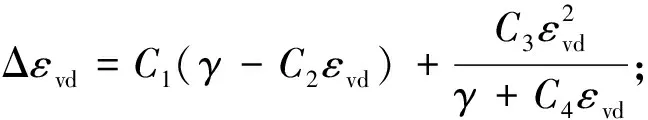
(5)

C1=7 600(Dr)-2.5；

(6)

C2=0.4/C1；

(7)

(8)

式中:Δεvd为土体塑性体积应变增量;C1、C2、C3和C4是Finn模型的控制参数;Dr为砂土的相对密实度;γ是土体的剪应变;εvd是土体的累计体应变。式(6)～(8)为C1、C2的Byrne改进计算式,C1、C2根据可液化土的修正标准贯入度击数计算。孔隙水压力变化值与土体塑性体积应变的关系为

(9)

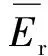
建立如图6所示的动力计算模型。根据可液化土的修正标准贯入度击数(N1)60=10.3,计算得到C1=0.472 7,C2=0.846 3。图8中的场地侧移随时间变化曲线可知场地最后的侧移值为15 cm, 是实测值的83%。

图8 Finn本构模型场地侧移随时间变化曲线Fig.8 Curve of lateral spreading versus time with Finn model

3 基于场地液化特征的计算方法

考虑场地的液化特性, 提出基于Newmark滑块法的侧移简化计算方法。传统的Newmark滑块法根据地表地震波和屈服加速度进行计算, 而侧移的本质是上层覆土沿着液化滑动面移动, 当液化发生时, 作用在滑动面的地震波使可液化土的强度快速衰减至残余强度并不断积累塑性位移。本文提出考虑场地液化特征的计算方法: 确定场地的液化土层、选用液化土层下地震波, 利用非线性分析方法分析得到液化土层下对应的地震波和场地的液化时间。将液化土层下对应液化后的地震波作为Newmark滑块法的输入, 根据液化土残余强度计算屈服加速度并计算场地侧移, 图9给出了基于场地液化特征的计算方法流程图。

图9 基于场地液化特征的侧移计算方法流程图Fig.9 Flow chart of the lateral spreading method based on site liquefaction characteristes

计算WLA液化台阵的场地侧移, 根据WLA液化台阵的二维非线性场地模型计算场地的液化时间, 利用PM4Sand本构模型模拟液化土, 根据液化土层超孔压比随时间的变化, 确定场地在17.7 s时发生液化。由于WLA液化台阵记录了Superstition Hills地震中的地震波, 因此无需计算液化土层下对应的地震波, 将IVW-090对应液化时间后的作为地震输入并记为IVW-090-3, 根据屈服加速度为0.03g, 计算得到侧移值并列于表4。可知, 应用简化计算方法计算得到的侧移平均值为22 cm, 是实测值的1.2倍。

表4 IVW-090-3地震波液化台阵侧移

4 侧移方法对比分析

由Newmark滑块法计算得到的侧移值为37 cm; 由数值计算方法所得侧移值分别为70和15 cm, 其中根据PM4Sand砂土液化模型所得侧移值为70 cm, 根据Finn孔压模型所得的侧移值为15 cm; 根据场地液化特征计算所得侧移值为22 cm。

传统的Newmark滑块法未考虑土体的非线性响应和地震输入的不确定性, 在侧移计算中, 土体被假定为刚体, 与实际情况不符。采用土体残余强度计算屈服加速度能够考虑土体强度的衰减, 现场记录的地震波作为地震输入能减少低地震输入的不确定性, 但其计算值较实测值偏大。对比由两个不同砂土液化模型计算得到的侧移值, PM4Sand的侧移值较大, Finn模型的较小, 由于不同的非线性本构模型的假设不同, 因此同一场地利用不同本构模型计算得到的侧移值不同。Finn 模型其实质是在莫尔-库伦模型的基础上考虑孔隙水压力变化, 而未考虑土体在循环荷载作用下的土体软化, 另外场地的液化侧移累计取决于场地的液化时间, 因此对同一场地, PM4Sand模型得到的液化侧移值较Finn模型的大, 而基于液化时间提出的侧移计算方法考虑了液化时间, 其得到的侧移值与实测值接近。 由于传统Newmark法未考虑孔隙水压力的变化和土体强度的衰减, 而数值计算能模拟场地的动力响应, 因此基于场地液化特征的计算方法计算得到的侧移值更合理, 为实测值的1.2 倍。

5 结 论

通过分析WLA液化台阵, 利用Newmark滑块法、数值计算方法并采用不同的液化土本构模型对该场地的侧移进行计算并与实测值进行对比。根据场地的液化特征, 提出基于液化时间的侧移简化计算方法。对比Newmark 滑块法、数值计算方法和基于液化时间的侧移简化计算方法的结果, 分析得到如下结论:

(1)Newmark滑块法未考虑土体的非线性响应, 在计算时存在一定的假设, 利用Newmark滑块法计算得到的场地液化侧移较实测值偏大。

(2)在数值计算方法中, PM4Sand和Finn本构模型均能够有效模拟砂土液化和孔压变化。 由不同本构模型得到的液化侧移值不同，根据PM4Sand本构模型计算得到的侧移值较实测值偏大, 而Finn本构模型计算得到的侧移值较实测值小。

(3)基于液化时间提出的侧移计算方法考虑了孔压的变化特征, 因此侧移计算值较Newmark滑块法更为合理, 由基于液化时间的侧移简化计算方法得到的液化侧移为实测值的1.2倍。

本文研究中仅对单个算例应用相关计算方法进行验证, 由于液化侧移受到场地的土层分布和地震输入影响, 需针对更多的算例开展相关研究。