一类Manning-Rosen-Yukawa叠加势的D维Klein-Gordon方程的散射解

2021-06-05刘显明刘友炜

湖北民族大学学报(自然科学版) 2021年2期

刘显明,刘友炜

(1.华中师范大学物理科学与技术学院，武汉 430079; 2.湖北民族大学信息工程学院，湖北恩施 445000)

长期以来，研究人员一直高度关注在非相对论和相对论量子力学系统中不同势能函数形式的波动方程的解[1-2].高维的波动方程的解也常应用于物理化学和高能物理学的研究[3].Klein-Gordon方程是相对论量子力学和量子场论中，描述不带自旋结构粒子的运动的相对论波动方程，是薛定谔方程的相对论形式[4].在研究具有特定势的波动方程时，研究人员提出了大量的有效方法并推广应用到了求解Klein-Gordon方程和Dirac方程这些相对论形式的薛定谔方程的求解.其中，典型方法有因式分解法[5-6]，特殊函数法(FAA)[7]，超对称法(SUSY)[8]，Nikiforov-Uvarov(NU)法[9]，渐近迭代法(AIM)[10]，等.

近年来，人们在研究非相对论和相对论波动方程中对Manning-Rosen势和Yukawa势进行了深入研究.Onate和Ojonubah[11]引入一种一般的Yukawa势并应用超对称法讨论了薛定谔方程的能量本征值.Ita等[12]第一次引入了一类由Manning-Rosen势和Yukawa势组合的叠加势，利用参数化的NU法求解了薛定谔方程的近似解析解.同时，研究人员进一步讨论了具有Manning-Rosen势和Yukawa势的相对论波动方程.文献[13-14]求解了具有一般的Yukawa势的Dirac方程的束缚态和散射态问题.文献[15-16]计算了具有Manning-Rosen势和Yukawa势这类指数势的Klein-Gordon方程的解析近似解.本文正是基于对Manning-Rosen势和Yukawa势的特别的研究兴趣，在文献[15-16]基础上提出一类由具有更加一般形式的Manning-Rosen势和Yukawa势的线性组合而得到的新的叠加势，并进而研究含有此类势的高维Klein-Gordon方程的散射态解.引入的新叠加势的形式为：

(1)

1 D维Klein-Gordon方程的分离变量

在球坐标系中，D维的Klein-Gordon方程可以写为：

(2)

(3)

(4)

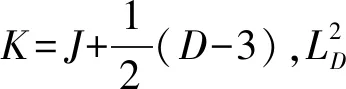
(5)

2 散射态的解析近似解

方程(5)中取S(r)=V(r)，同时引入Manning-Rosen势和Yukawa势的线性叠加势(1)，Klein-Gordon径向方程可写成：

(6)

(7)

和Pekeris近似[18]：

(8)

考虑到Pekeris近似公式中c0参数的存在不适宜求散射态，本文将采用Greene-Aldrich近似公式，即：

(9)

图中应用Greene-Aldrich公式选取了不同的参数值α=0.1，0.3，0.5,0.7，0.9作图与离心项精确值进行比较.图1 离心项Greene-Aldrich近似函数Fig.1 The centrifugal term with Greene- Aldrich approximation function

正如图1所示，当αr较小时，式(9)和离心项的精确值符合得非常好，因而这类近似可以很好地研究粒子之间的短程相互作用.

将方程(9)代入方程(6)可得：

(10)

然后，对上式自变量做指数变换，引入新的自变量z=1-e-2αr(r∈(0,∞),z∈(0,1))，并代入方程(10)，化简可得：

(11)

其中，

(12)

对于满足边界条件(11)的方程的径向波函数，可以按“K/2π标度”标度的归一化超几何函数表示.现在可以设波函数的形式为：

uvJ(r)=(1-z)-iβzλu(z).

(13)

其中，

(14)

(15)

把方程(13)代入式(11)可得：

z(1-z)u″(z)+(2-2λ-z(3+2β-2λ))u′(z)-(a2+(1+β-λ)2)u(z)=0.

(16)

方程(16)为超几何微分方程，其解可以表示为：

(17)

其中参数为：

(18)

利用方程(13)、(14)、(15)、(17)和(18),可以得到径向波函数的散射态解为：

(19)

其中，Ν是归一化常数.

接下来，将利用散射态波函数的渐进行为确定归一化常数Ν和相移δl的解析表达式.根据超几何函数2F1(a,b;ε;z)的性质：

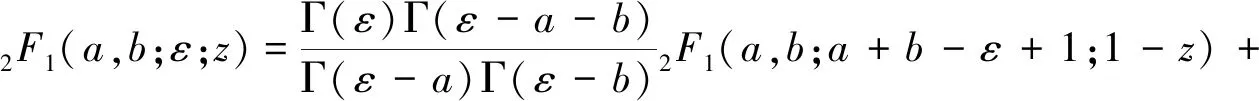
(20)

和2F1(a,b;ε;0)=1，可以得到：

(21)

利用关系式

(22)

和方程(18),可以得到:

(23)

其中，θ为常数.

下面，把方程(22)、(23)代入方程(19),可以得到：

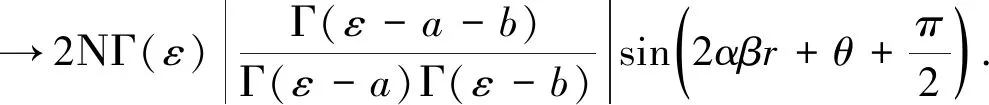
(24)

(25)

(26)

接下来，根据散射态和束缚态的关系，利用方程(25)中伽马函数的性质，可计算得到能量本征值满足方程:

(27)

把(12)、(14)、(15)、(18)代入(27)，可以得到:

(28)

此即为相对论情况下能量束缚态所满足的方程.考虑到ν≡n=0,1,2,3,…，可见式(28)与附A中利用参数化NU法计算得到的束缚态结果(37)一致.

于是，利用相对论和非相对论的对应关系

(29)

可以很容易计算得到非相对论的束缚态转动振动能量谱满足的方程:

(30)

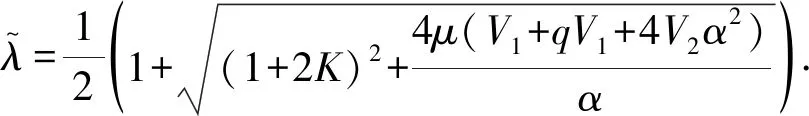
3 结论

本文提出了一种新的Manning-Rosen势和Yukawa势的线性叠加势，应用超几何方法得到了D维Klein-Gordon方程散射态的解析近似解和束缚态能量谱.本文的计算方法极大地简化了求解类薛定谔波动方程的散射态和束缚态的求解过程.文中在解析推导的过程中采用了Greene-Aldrich提出的优化的指数近似公式来模拟离心项势能.这种解析的近似与α较小的短程相互作用势能吻合的较好，因而本文的结果还可以进一步用来研究高能物理中强子的相互作用.