基于GA-LSTM的高层建筑结构地震响应的分散控制研究

高经纬， 涂建维， 刘康生， 李 召

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070)

针对土木工程结构振动的主动控制，传统方法多采用基于“分散采集，集中控制”思想的集中化控制策略[1-2]。随着施工技术的发展，建筑结构的体量和复杂程度不断提高，传统方法暴露出计算成本大、可靠度较低等弊端[3]，因此，基于大系统理论的分散控制策略得到各国学者高度的关注。潘兆东等[4-5]将大系统理论分别和PID(proportional integral derivative)、模糊滑模控制结合，构造不同的分散控制器，对9层Benchmark模型进行仿真，验证了提出分散控制方法较集中控制具有更好的减振效果；Amini等[6]提出一种基于夹杂原理的多叠层钢结构分散脉冲控制方法，并对钢结构模型进行仿真，结果表明，该方法在不同工况下均能有效降低结构响应。以上结合传统算法的分散控制需建立精确的数学模型，结构、数据的复杂性和不确定性可能导致系统的不稳定和控制性能的失效。因此，现行方法更倾向于神经网络等智能分散控制。如Lopez-franco等[7]提出了一种利用离散递归高阶神经网络和扩展卡尔曼滤波算法的最优分散控制法，实现了损失函数的最小化和多智能体系的稳定化。

但是，人工神经网络在其发展历程中仍存在过拟合和局部最优等问题[8]。为解决这些问题，深度学习的概念被Hinton等[9]提出，并被逐渐运用于智能控制领域。如Zhang等[10]将深度学习中的卷积神经网络(convolutional neural network，CNN)运用于机械手臂的抓取目标识别，提高了抓取精度和速度；Li等[11]使用循环神经网络(recurrent neural network，RNN)构建机器人的控制力预测模型，提高了机器人的定位精度。本文研究的长短时记忆(long short-term memory，LSTM)[12]网络是RNN的改良模型，能有效解决RNN训练梯度爆炸或消失问题，更适用于时间序列数据的预测[13]。如Wang等[14]使用Pinball损失函数代替均方误差，提出LSTM分位数形式的概率预测法，应用于个体形式的概率负荷预测，取得优于同类算法的预测效果；涂建维等[15]使用LSTM网络模型预测控制器的实时控制力，提出了一种基于LSTM的结构集中控制算法，并通过3层Benchmark 模型进行算法验证。目前，深度学习在控制领域的研究较少，针对建筑结构的振动控制研究几乎为空白。

同时，LSTM进行深度学习时所涉及的超参数众多，而这些参数决定了深度学习框架的性能，以往多采用经验或试算取值，效率和精度都很低。袁磊等[16]使用遗传算法(genetic algorithm，GA)优化自编码列车自保护(automatic train protection，ATP)车载设备的测试序列，提高了网络决策精度和编码稳定性；Kanada[17]提出一种基于GA的CNN反向传播学习方法，通过遗传变异和位置控制并行搜索，解决了学习速度调度和搜索局域性控制问题。因此，将GA用于深度学习的参数优化是可行且有效的。

综上，经过GA优化后的LSTM，具有数据特征提取精确、可进行长期时间序列预测、可拟合高度非线性函数等特性，因此将其应用于建筑结构的振动控制领域是具有研究价值的。本文在原有研究的基础上，以地震作用下的高层土木工程结构为研究对象，提出基于LSTM的智能分散控制策略，分别设计出多种重叠分散、独立分散LSTM控制器，结合Lyapunov稳定性理论和GA对LSTM的深度学习超参数进行线下优化，最后对20层Benchmark模型施加不同地震波进行仿真计算，并与LQR(linear quadratic regulator)集中控制算法进行控制效果对比，验证GA-LSTM分散控制策略的可行性和有效性。

1 大系统分散控制模型

假设被控K层高层建筑结构的作动器满布，并分散为N个子系统，且各个子系统之间没有重叠。第i个子系统包含k个楼层，其位移向量Xi与控制力向量Ui分别为

(1)

状态空间方程为

(2)

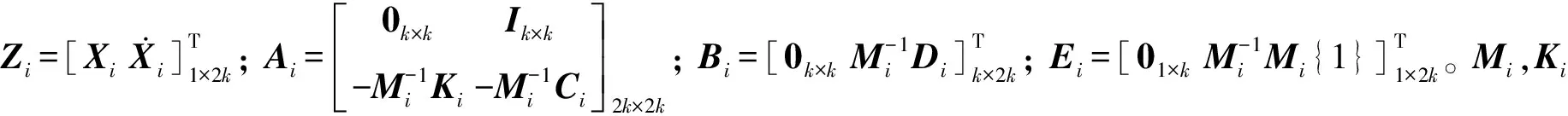
若N个子系统之间存在重叠，我们通过解耦-扩展-收缩的步骤可设计重叠分散子系统控制器。考虑将大系统分散成链型拓扑结构，该类型结构具有仅在相邻子系统间进行信息互联、共享的特点，即系统矩阵A满足下式[18]

(3)

(4)

(5)

(6)

其中，

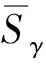
(7)

LSTM分散控制系统原理如图1所示[23]。完全分散控制见图1(a)，各子控制器平行工作，不存在从属关系，仅依靠自身结构属性和独立观测信号实时输出控制力，系统设计较为简单；重叠分散控制见图1(b)，各子控制器间需进行结构响应等信息的交换，结合自身和相邻子控制器边界观测信号而制定控制策略，系统设计较为复杂。由解耦后的状态空间方程和控制力位置矩阵可知，相邻子系统对i子系统的影响主要在边界层，可视为未知干扰，对内部核心楼层的影响较小。

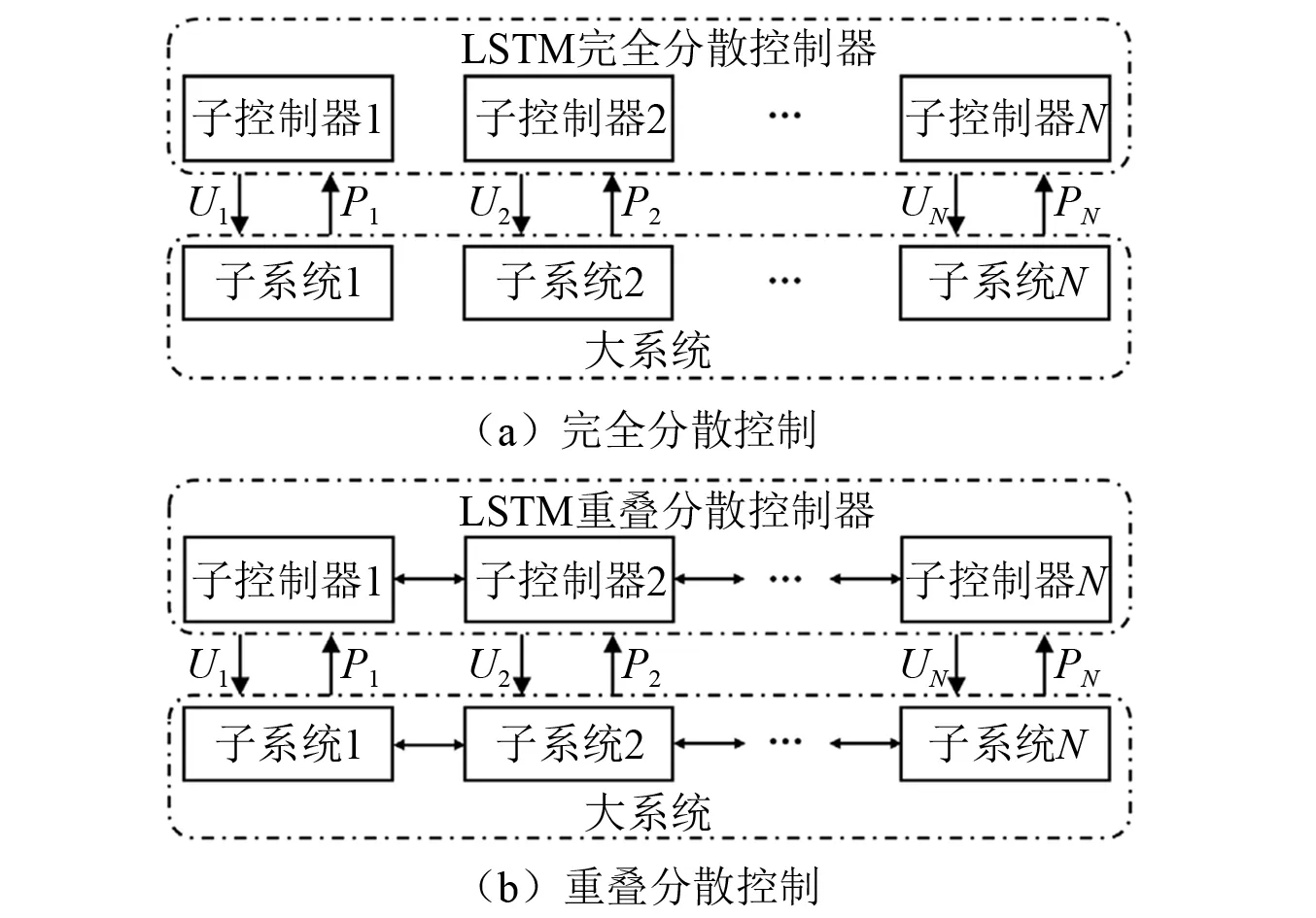
图1 LSTM分散控制系统原理图Fig.1 LSTM distributed control system schematic diagram

2 GA-LSTM智能分散控制算法

基于GA-LSTM的结构智能分散控制算法是以LSTM深度学习框架为核心，以建筑结构在地震作用下的振动为控制背景，设计出不同类型的LSTM子控制器，再使用GA算法进行超参数优化，进而搭建适用于高层建筑结构抗震的分散控制系统。

2.1 LSTM子控制器设计

LSTM是RNN的变型，优化了框架的长期记忆能力，提高了深度学习的稳定性能。LSTM子控制器的主要计算板块包括前向核心算法、误差反向传递和优化处理器。其中，每一个LSTM隐层的前向核心算法包含4个交互单元，分别为输入门、输出门、更新门和遗忘门，并在RNN基础上添加了随时间序列更新的细胞储存单元。t时刻j子结构的LSTM控制器计算公式[24]分别为

fj,t=σ(Wj,f·[hj,t-1Pj,t]T+Bj,f)

(8)

ij,t=σ(Wj,i·[hj,t-1Pj,t]T+Bj,i)

(9)

(10)

(11)

oj,t=σ(Wj,o·[hj,t-1Pj,t]T+Bj,o)

(12)

hj,t=oj,t*tanh(cj,t)

(13)

将结构各层的位移、速度、加速度响应和地震加速度作为LSTM输入，即第j个子结构LSTM控制器在t时刻的输入Pj,t为

(14)

Uj,t=hj,t=G(Pj,t-1)

(15)

式中：G(·)为由LSTM拟合的高度非线性函数。在重叠分散控制系统中，假设重叠部位所受控制力方向与结构振动方向相反，定义相邻子系统重叠作动器的控制力输出为

(16)

式中： sgn(·)为符号函数；uj,k为第j个子系统中编号为k的重叠作动器控制力； ∇(·)含义为

(17)

LSTM子控制器内部结构如图2所示。

LSTM子控制器中误差反向传递的步骤为：分别计算每时刻式(9)～式(14)的输出值；分别以时间和网络层级作为反向传播方向计算各LSTM单元误差；由误差反算LSTM隐层各单元权重；最后使用优化处理器更新单元权重。本文提出的LSTM分散子控制器中，LSTM深度学习框架的网络结构组成分别为：序列输入层、长短时记忆网络层、防过拟合层、全连接层及回归层；误差反向传递采用随时间反向传播(back-propagation through time，BPTT)算法；优化处理器采用适应性动量估计(Adam)算法。

图2 LSTM子控制器内部结构Fig.2 LSTM sub controller internal structure

2.2 LSTM子控制器稳定性分析

根据Lyapunov稳定性理论对LSTM子控制器的稳定性进行分析，推导出子控制器稳定的充分条件，也为后续使用遗传算法对LSTM深度学习框架进行超参数优化提供理论依据。设控制器输出误差为

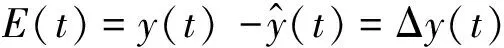
(18)

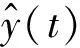
ζ(t)=E2(t)/2

(19)

神经元激活函数在取样频率足够高的情况下求导，有

σ′(t)=Δy(t)/Δu(t)|Δt→0=dy(t)/du(t)

(20)

并满足

∂E(t)/∂W=-σ′(t)∂u(t)/∂W

(21)

式中：u(t)为控制器输入值；W为权重系数矩阵。由2.1节，误差反向传递采用BPTT算法，结合式(19)～式(21)，推导LSTM权重系数矩阵更新公式为

(22)

式中： Δwji(t)为第i个神经元到第j个神经元的改变量；α为学习率； 其他参数含义同2.1节。为推导LSTM分散控制中每个子系统的控制律，构造Lyapunov函数形式为

V(t)=E2(t)/2

(23)

根据式(21)得到Lyapunov函数的变化量形式为

(24)

式中： ‖·‖为Euclidean范式； 设l(t)=∂u(t)/∂net；g(t)=∂u(t)/∂W[27]； 为保证系统稳定性，需满足ΔV(t)<0，即

ρ=α{α·[σ′(t)]2·h2(t-1)·‖l(t)‖2·‖g(t)‖2-
2h(t-1)·‖l(t)‖·‖g(t)‖}<0

(25)

整理得

0<α<2/[σ′(t)]2h(t-1)l(t)g(t)

(26)

即初始学习率满足式(26)时，LSTM子控制器是稳定的。

2.3 GA-LSTM超参数优化

由2.2节知初始学习率α同时对LSTM子控制器稳定性有较大影响。LSTM深度学习框架中，初始学习率是一个重要的超参数，它控制着损失梯度调整网络权值的速度。初始学习率过小时，损失梯度下降速率降低，收敛时间更长；过大时，梯度下降过程可能会跨过最优值。因此，对于初始学习率α的优化是必要的。

目前，针对深度学习中初始学习率等超参数的调节，没有具体理论进行取值，更多的是通过试算和经验取值。本文提出基于遗传算法的初始学习率α优化，适应度函数采用LSTM深度学习框架的损失函数，公式为

(27)

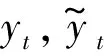
图3 GA-LSTM超参数优化流程图Fig.3 GA-LSTM hyperparametric optimization flow chart

3 仿真分析

3.1 结构模型及控制分散工况

选用ASCE提出的20层Benchmark模型作为仿真算例，假定楼板水平刚度无穷大，采用静力凝聚法对有限元模型进行降阶，仅保留20个平动自由度，作动器各层满布。缩聚后的Benchmark结构参数[28]见表1。

表1 Benchmark模型参数Tab.1 Benchmark model parameters

通过不同划分方式，将运用于Benchmark模型的LSTM智能控制器分别设计为多种分散控制形式：完全分散-20个子系统(工况1)、部分独立分散-4个子系统(工况2)，用以研究子系统数量对控制效果的影响；链型拓扑重叠分散-5个子系统(工况3)，与工况1、工况2进行对比，研究是否有控制器重叠的影响；链型拓扑重叠分散-6个子系统(工况4)，与工况2、工况3进行对比，研究重叠控制器数量的影响。各工况子系统分布简图如图4所示，并与LQR集中控制(工况5)进行对比研究。

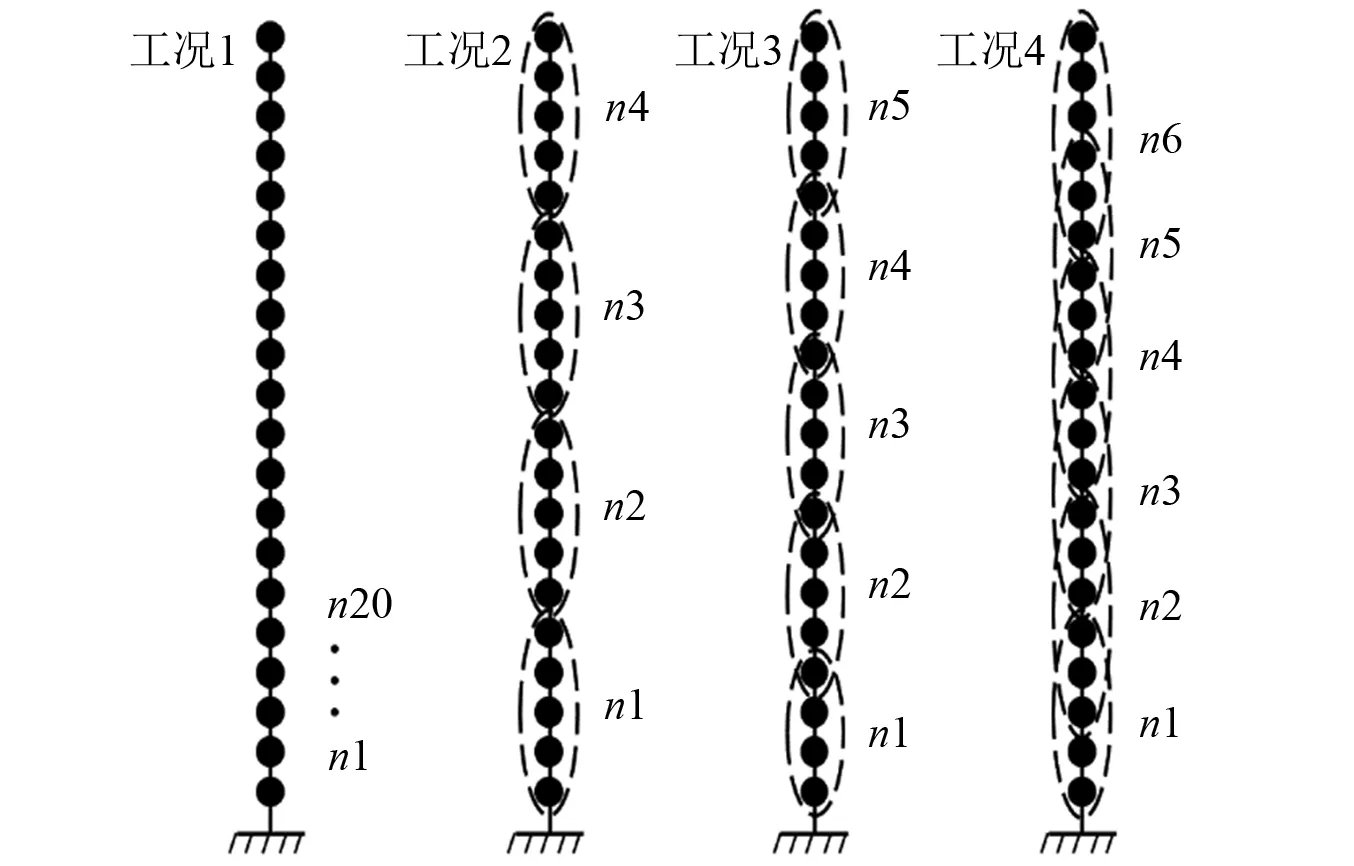
注：ni为各子系统编号。图4 各分散工况子系统分布简图Fig.4 Distribution diagram of subsystems under different dispersed conditions

工况1的网络结构为4×30×1，工况2为16×100×5，工况3分别为16×100×5和13×100×4，工况4为19×100×6和16×100×5(隐层仅列出LSTM层)。其中，LSTM层单元节点数均由经验和试算相结合的方法确定，使LSTM预测框架的损失函数最小，控制器控制力输出效果最优。工况1～工况4中，GA-LSTM深度学习预测框架的构建采用中等周期强震记录-El-centro波，设定采样周期为0.02 s，计算时间为30 s，训练数据集均为LQR控制算法计算数据的前1 000组，共计61维，依次是结构位移响应(20维)、速度响应(20维)、加速度响应(20维)和地震加速度(1维)。根据不同工况的网络结构，将训练数据进行不同方式的划分。

以工况3为例。数据训练前进行Max-min归一化处理；将上一时刻结构模型的各层响应和地震加速度作为LSTM框架输入，分别提取5个子系统所包含楼层的相应训练数据，数据维度从下至上依次为13，16，16，16和16维(各子系统的训练数据均包含1维地震加速度，各楼层均包含3维结构响应，如13=4×3+1)；根据式(15)拟合相应的高度非线性函数Ui,t=Gi(Pi,t-1)(i=1,2,…,5)，用于计算下一时刻各楼层的控制力，并将其作为预测输出(不被观测，也不作为下一时刻LSTM预测的参考数据)；预测框架构建完成后，将其编译至Simulink中，完成GA-LSTM智能分散控制器的设计；详细运算过程如下。

首先，根据式(4)～式(7)将20层benchmark模型的整体控制系统解耦为5个链型拓扑重叠子控制系统，相邻子系统间分别有1个重叠控制器，并由式(14)得各子系统t-1时刻的输入矩阵

(28)

(29)

式中，相邻控制力矩阵间均有1维控制力向量(1个重叠楼层)的重合。接着，将上述各控制力矩阵的重叠部分—u1,4与u2,1、u2,5与u3,1、u3,5与u4,1、u4,5与u5,1进行数据处理，相关计算方法及变量含义同式(16)和式(17)。最后，将各楼层控制力向量合并，即可得到20层Benchmark模型的最终控制力矩阵。

工况1、工况2不考虑系统重叠问题(重叠楼层为0)，因此各子控制系统的输出并集[U1U2…U20]T，[U1U2U3U4]T即为工况1、工况2的最终控制力矩阵；工况4与工况3相比，子控制器数据维度提高1维，重叠楼层增加到3层，重叠部分的控制力计算原理同上，不做赘述，最终控制力矩阵为[U′1U′2…U′6]T， 其中U′i(i=1,2,…,6)，表示重叠数据合并处理后的子系统控制力矩阵。

3.2 GA-LSTM子控制器优化

根据2.3节提出的GA-LSTM超参数优化方法，使用软件MATLAB编写GA算法程序优化LSTM子控制器的初始学习率α。选择算子采用排序选择，交叉算子采用单点交叉，变异算子采用均匀变异，采用轮盘赌法选择新个体，适应度函数采用式(27)。初始参数经试算后设置：进化代数取80次，交叉概率取0.1，种群规模取8，变异概率取0.01，使各LSTM子控制器的适应度函数均达到最小值。4种工况的LSTM子控制器种群进化图如图5所示。

图5 种群进化曲线Fig.5 Population evolution curve

经遗传算法优化后工况1～工况4的最优初始学习率分别为0.006，0.010，0.006和0.040，迭代80次后的最优适应度即为LSTM控制器损失函数值，分别为8.3×10-5，2.3×10-4，2.2×10-4，3.0×10-4，均取得了较好的预测效果，相对常用的试算方法提高了计算效率和计算精度。

3.3 GA-LSTM分散控制效果比较与分析

在验证提出的智能分散控制算法控制效果的同时，为研究GA-LSTM深度学习框架的泛化、自学习能力，分别选用El-centro波(加速度峰值为3.417 m/s2)和汶川波(3.048 m/s2)作为外部激励，持时均为30 s。将各类型的GA-LSTM分散控制结果与LQR集中控制进行比较，Q和R权矩阵的常系数分别取2×104，6×10-6。5种工况下各集中、分散控制器对20层Benchmark模型的减震率见表2。由表2可知：不同地震波激励下，GA-LSTM智能分散控制算法能够稳定地大幅抑制结构各楼层的振动响应；分散控制针对结构响应峰值可达到与集中控制相近的减震效果；重叠分散的楼层越多，平均减震率越接近集中控制。

图6、图7分别为El-centro波、汶川波作用下，结构各层的位移、加速度响应和控制器控制力的峰值大小。

由图6、图7知：GA-LSTM智能分散控制算法对各楼层位移响应的控制效果相比对加速度的控制效果发散性更小；完全分散、部分独立分散控制不考虑楼层间或各子控制器间的关联耦合，仅依赖相应控制器的反馈信息，响应、控制力峰值沿楼层变化幅度较大；链型拓扑重叠分散考虑子控制器间的信息交叉反馈，响应、控制力峰值沿楼层变化更平稳，控制结果与LQR集中控制更接近，相比无重叠分散控制具有更强的适用性。

表2 不同工况下各控制器的控制效果Tab.2 Control effect of each controller under different working conditions %

上述数据仅从响应峰值的角度反映算法的控制效果，为进一步研究算法对建筑结构时程响应的影响，参考文献[29]给出对Benchmark模型的时程评价指标，公式为

(30)

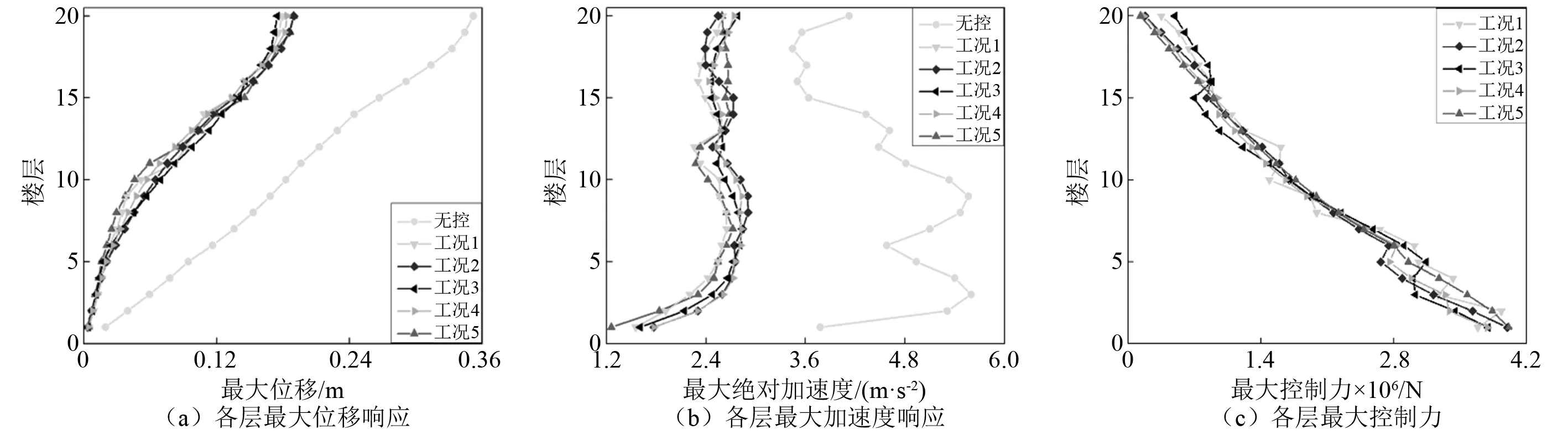
图6 El-centro波作用下结构各层响应及控制力Fig.6 Responses and control forces of different layers of structures under El-centro wave

图7 汶川波作用下结构各层响应及控制力Fig.7 Response and control force of different layers of structures under Wenchuan wave

由表3可得：不同构造形式的GA-LSTM分散控制器对20层Benchmark模型的时程响应控制均有较好效果；4种GA-LSTM分散控制器均具有良好的泛化、自学习能力；工况1～工况4在不同地震作用下的时程评价指标总和相比工况5分别降低8.8%，9.1%，7.5%和3.1%，即6个子系统的重叠分散控制器更接近LQR集中控制的控制效果，表明重叠分散控制器对时程响应的控制效果比无重叠分散控制器更好。

表3 不同地震激励下时程评价指标Tab.3 Time-history evaluation index under different earthquake excitation

4 结 论

本文结合LSTM方法和大系统分散控制模型，设计了适用于高层建筑等大型土木工程结构振动控制的LSTM分散控制器。同时，根据Lyapunov稳定性理论对LSTM分散控制器的稳定性进行分析，采用遗传算法对LSTM超参数进行优化。最终，提出基于GA-LSTM的智能分散控制算法，并对20层Benchmark模型进行不同工况的控制对比分析。仿真结果表明：

(1) GA-LSTM智能分散控制与LQR集中控制效果相仿，均能大幅抑制地震作用下的结构响应，提高了算法可靠性，证明该算法是有效的、可行的。

(2) 利用遗传算法对LSTM深度学习框架的超参数进行优化，相比试算和经验取值提高了算法的计算效率和计算精度，使各GA-LSTM子控制器处于更高效的工作状态。

(3) 不同结构形式的GA-LSTM智能分散控制算法，因计算原理有本质区别，导致在控制输出和结构控制效果等方面均有差异。计算结果表明，链型重叠分散控制较无重叠分散控制的控制效果更好，适用性更强。本文将深度学习中的长短时记忆网络引入结构振动控制领域，为高层建筑结构的分散振动控制提供了一种新思路。