分布式流体脉动压力激励下泵喷推进器的结构辐射噪声分析

黄修长， 师帅康， 苏智伟， 饶志强， 华宏星

(1. 上海交通大学 振动、冲击、噪声实验室，上海 200240；2. 上海交通大学 机械系统与振动国家重点实验室，上海 200240； 3. 江南造船(集团)有限责任公司 江南研究院，上海 201913)

螺旋桨、泵喷等推进器在表面脉动压力激励下：一方面会产生结构振动直发声以及流噪声直发声；另一方面会通过轴系传递激励艇体，会导致艇体产生强烈的声辐射，螺旋桨/泵喷等推进器-轴系-艇体的耦合振动声辐射研究受到广泛关注[1-3]。推进器引起的耦合振动噪声问题包含推进器运转时流体表面脉动压力的获取、推进器的流固耦合结构动力学模型以及流体脉动压力激励下推进器-轴系-艇体的振动声辐射等研究。

在推进器运转时流体表面脉动压力的获取方面，螺旋桨激励力的获取方法有计算流体动力学(computational fluid dynamics, CFD)数值模拟[4]、基于势流理论的面元法[5]等试验方法。势流理论能够获得推进器在尾流场中的脉动压力线谱特征；CFD方法中DNS(direct numerical simulation)方法和LES(large eddy simulation)方法可获得湍流脉动压力，RANS(Reynolds-averaged Navier-Stokes equations)方法可获得平均速度和压力，无法考虑湍流脉动压力；也可采用势流理论-黏流混合方法[6]；试验方法主要用于获取水动力性能，仅能获得推进器传递给轴系的脉动推力，仍无法准确获取推进器表面脉动压力[7]。

在推进器的流固耦合结构动力学模型建模方面，螺旋桨可采用实体单元进行有限元模拟、采用等效质量-弹簧单元[8]、等效质量-梁-质量单元[9-10]进行模拟。泵喷推进器一般需采用有限元模拟。

流体脉动压力激励下推进器-轴系-艇体的振动声辐射计算模型中，螺旋桨的激励力通常考虑集中力采用等效的方法施加在压力面中线沿着半径方向0.7R处(R为转子半径)[11]，或考虑随机宽带力采用条带的方法进行施加[12]，或利用面元法考虑激励力的线谱采用耦合有限元/边界元的方法进行施加[13-14]。

实际上推进器的脉动压力是在导管、定子、转子吸力面和压力面上呈复杂空间分布的力，不同模态在空间分布力作用下会激励起复杂的响应。采用流固耦合分析方法可以建立推进器的流固耦合模型、考虑分布式脉动压力作用下的结构振动声辐射[15-16]，但流固耦合分析方法需要大量的计算资源。Wei等[17]利用CFD获得了螺旋桨表面的脉动压力，利用耦合有限元方法建立了螺旋桨流体脉动激励下的桨轴艇耦合系统振动声辐射模型，但是计算时将激励力作为集中力等效，未考虑分布式脉动压力的影响，同时作者们也指出需考虑流体脉动压力的分布特性。本文考虑实际推进器的脉动压力分布，通过插值方法把流体脉动压力映射到推进器结构网格上，获得了在分布式流体脉动激励力作用下推进器的结构振动声辐射以及通过轴承的传递力。通过将分布式流体脉动激励作用下的响应结果和工程中通常采用的等效激励力作用下的响应结果进行对比，研究了分布式流体脉动激励力的影响。

1 理论基础

1.1 基于CFD的螺旋桨表面脉动压力计算

不考虑推进器内部流场空化影响，可假设流体为不可压缩黏性单相流，基于RANS的控制方程可写为

(1)

(2)

(3)

式中：k为雷诺时间平均下湍流动能；ε为湍流耗散率；Cμ=0.09。

1.2 推进器表面脉动压力激励下推进器-轴系-艇体的耦合振动声辐射

采用耦合有限元分析方法进行推进器的流固耦合结构振动响应计算，其动力学方程为

(4)

式中：X为结构的位移向量；F为推进器结构表面的流体脉动激励力向量；p为流场中的声压向量；M和K分别为泵喷结构的质量和刚度矩阵；C为阻尼矩阵，C=αM+βK；Ma和Ka分别为流体的质量矩阵和刚度矩阵；H为流固耦合矩阵；Π建立了结构湿表面上的节点法向位移与结构振动位移向量X之间的关系，各个表达式为

(5)

式中：N和Nψ分别为结构和流体的插值型函数；ρa为流体密度；Aa和Va分别为推进器与流体接触的湿表面和声学流体区域；c为流体中波速。

由式(4)可以求得推进器模型中所有节点的位移响应。利用Π矩阵获得推进器湿表面上第i个单元第α个节点的法向振速viα，然后利用直接边界元法求得边界上的声压piα以及远场场点pj分别如式(6)和式(7)所示

(6)

(7)

其中，

1.3 流体脉动压力和结构表面节点力映射

将流体模型中转子、定子、导管表面单元的压力以及结构模型表面的节点导出，通过径向基函数插值将流体单元节点的压力映射到结构节点上。径向基函数插值基本原理为：假设空间存在一组点群xj及点群上的函数值fj(j=1,2,…,N)，可构建各点之间的距离函数φ(‖x-xj‖)与函数值之间的关系[18]

(8)

式中： φ(‖x-xj‖)为径向基函数，是插值点与目标点之间距离的函数；λj为径向基函数的系数。通过xj可以建立点群之间的λj系数求解线性方程组。空间任意点上的函数值f(x)则可以通过式(8)求解。具体计算时首先找到结构面单元中心附近的一组流体节点及压力值并求解径向基函数插值系数，然后将结构面单元中心代入式(8)中求解结构面单元上的压力分布。本文中径向基函数的基函数为

φ(‖x‖)=(1-‖x‖)4(4‖x‖+1)

(9)

在求得结构面单元的压力分布后，将压力乘以面积得到面单元上的集中力，将集中力按节点数平均分配到各个节点上，即可得到每个结构单元节点上的集中力分布。在每个时刻进行径向基函数插值即可得到时域中结构节点的集中力。

2 数值模拟和分析

2.1 模型描述

针对某7叶转子5叶前置定子泵喷推进器进行计算，推进器的流体模型CFD数值求解采用商业软件ANSYS Fluent进行，采用标准k-ε湍流模型，压力、速度耦合求解采用SIMPLEC (semi-implicit method for pressure-linked equations consistent)方法，其他项均采用二阶迎风格式。数值模型计算域划分为静止域和旋转域，叶片所在旋转域设置为滑移网格，两个计算域之间的交界面设置为interface边界条件进行数据传递。如图1(a)所示，计算中远前方入口设置为速度入口条件，远后方出口设置为压力出口条件，外围远场边界为速度入口条件，转子、定子及导管等固体表面采用无滑移固体壁面条件。图1(b)为部分进行流体计算的面网格。非定常计算转子转速为900 r/min，时间步长为1.851 85×10-4s，保证转子每个时间步旋转1°，计算的最高频率为2 700 Hz，采样频率为5 400 Hz。数值计算的收敛性残差满足：连续性残差收敛在10-5以下，三个方向速度残差均在10-6以下，湍动能k的残差低于10-7。

结构振动响应采用软件Abaqus进行计算，结构模型如图1(c)所示，水体直径为转子外径6倍。推进器的定子底部固定以模拟固定支撑在艇壳上；推进器转子桨毂前端在中心处采用三向弹簧支撑，弹簧三向刚度为轴系、轴承的等效刚度，分别为7.2×109N/m，8.0×109N/m，8.0×109N/m。推进器的材料为钢，密度为7 850 kg/m3，弹性模量为2.1×1011Pa，泊松比为0.3。针对施加在结构湿表面节点的脉动压力进行傅里叶变换获得频率域内的脉动压力，开展谐响应计算获得推进器的振动响应及传递力。

将泵喷推进器的振动响应导入Virtual Lab，开展直接声辐射计算(声网格如图1(d)所示)，获得声辐射响应，取出推进器的表面均方振速和辐射声功率，以对推进器的水下辐射噪声特性进行评价。

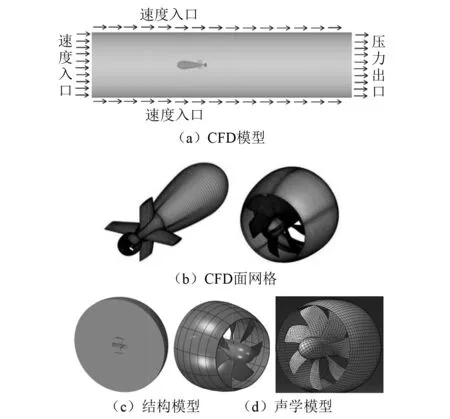
图1 流体模型和网格、结构和声学模型Fig.1 CFD modeland mesh,structural model and acoustic model

2.2 推进器表面脉动力分析

对插值的结果进行校核。选择非定常计算中时间步为7 200步的插值结果与CFD中的结果进行对比，如图2所示。插值前后导管、转子的压力分布基本一致、最大最小值处于同一量级。径向基函数插值可较精确地获得结构单元节点上的输入载荷。

图2 CFD网格和结构网格表面压力分布Fig.2 Pressure distribution on CFD mesh, structural mesh

取出插值后单个叶片三向脉动力的时域结果进行比较，如图3所示。三向脉动力的插值结果均与CFD计算的结果吻合好，纵向脉动推力插值结果与CFD计算的结果相差了黏性力。给出了傅里叶变化后的脉动推力结果，可见脉动推力主要为4倍轴频及10倍轴频，叶频105 Hz及其倍频并不明显，这主要是舵翼个数为4、前置定子数为5所致。

对7个叶片的三个方向的脉动力分别求和得到转子总的三个方向的脉动力，如图4所示。转子总的垂向力和总的侧向力的平均值相对于推力的平均值较小，脉动值相比推力的脉动值较小。对于脉动推力而言，插值前后压差产生推力相差0.8%，主要是由于插值时忽略了黏性力造成的。脉动总推力主要以叶频105 Hz及5倍叶频524.7 Hz为主，这是因为泵喷推进器为5叶前置定子(频率有些许差别主要是由于傅里叶变换时的频率分辨率所致)。

图3 插值后单个叶片的脉动力Fig.3 Pulsation force of a single blade after interpolation

图4 插值后推进器转子脉动力Fig.4 Pulsation force of the propeller after interpolation

2.3 结构振动湿模态分析

针对建立的泵喷推进器开展湿模态分析，得到湿模态结果如图5所示，给出了各阶模态的频率结果。可见，泵喷推进器主要存在转子的弯曲和扭转、导管的圆柱模态、定子的弯曲、转子和导管的耦合模态、定子和导管的耦合模态等典型模态。

图5 泵喷推进器的典型结构模态Fig.5 Typical structural modes for pump-jet

2.4 不同流体脉动激励施加方法下推进器的结构辐射噪声分析

采取不同的激励加载方式：在泵喷表面分布式脉动激励力、转子表面分布式脉动激励力、转子0.7R处三向等效激励力和转子桨毂处三向等效激励力，获得泵喷推进器的结构辐射噪声，如图6和图7所示。可见泵喷推进器的结构辐射噪声频谱特征中既包含14.44 Hz，105.00 Hz，524.70 Hz等激励特性(轴频和叶频等)；也包含198.59 Hz(导管模态)，375.91 Hz(导管模态)，463.58 Hz，916.51 Hz(转子模态)等结构特性。由图6可知，与全部表面分布式激励的辐射声功率和均分振速相比，转子表面分布式激励的贡献远大于导管和定子表面脉动压力的贡献。

由图7可知，采用转子0.7R处施加等效激励力可以有效地反映转子表面分布式脉动激励力作用下的特征，但是各峰值处量级上比转子表面分布式脉动激励力作用下的响应小。在转子桨毂处施加等效激励力在特征和量级上将产生较大的差别，如轴频、叶频和一些特征模态处的响应幅值差别较大。

图6 泵喷表面和转子表面分布式脉动激励力激励下的结构辐射噪声Fig.6 Vibro-acoustic responses under distributed hydrodynamic excitation forces of pump-jet or propeller

图7 转子表面不同激励力作用下的结构辐射噪声Fig.7 Vibro-acoustic response under different excitation forces on the propeller

2.5 不同流体脉动激励施加方法下推进器的传递力分析

分布式和等效转子表面脉动力作用下通过弹簧的三向传递力结果，如图8所示。传递力的频率特征和声辐射结果的特征相似。对纵向传递力，在转子0.7R处施加等效激励力所得到的特征与转子表面分布式脉动激励力作用下的基本一致，能够体现出结构模态和激励力峰值，并且幅值接近；但对垂向和侧向传递力，在转子0.7R处施加等效激励力所得到的特征与转子表面分布式脉动激励力作用下的相差较大，幅值上差别更大。在转子桨毂处施加等效纵向激励力得到的三向传递力在特征和量级上都会和转子表面分布式脉动激励、转子0.7R处施加等效轴向激励相差较大。这主要是由于分布式激励的相位特性对结构动态响应的影响较大，桨毂处的等效激励力由于相位抵消无法考虑相位的影响，并且转子空间分布的模态对从叶片上不同激励点到桨毂的振动传递起到增强或削弱的滤波效应，分布式激励激励起的推进器模态更为丰富。

图8 转子表面不同激励力激励下的三向传递力Fig.8 Three directional transmitted forces under different excitation forces on the propeller

3 结 论

针对某型泵喷推进器在分布式流体载荷激励下的结构声辐射问题，利用径向基函数建立流体节点与结构表面节点之间的映射关系，获得了插值后CFD计算获得的结构表面分布式流体脉动激励力，开展了泵喷表面分布式脉动激励力、转子表面分布式脉动激励力、转子0.7R处等效轴向激励力和转子桨毂处等效轴向激励力作用下泵喷推进器的结构辐射噪声计算。得到以下结论：

(1) 所建立的流体节点与结构表面节点之间的映射关系具有较高的精度。

(2) 泵喷推进器的结构声辐射响应中，转子表面分布式激励的贡献远大于导管和定子表面脉动压力的贡献。

(3) 对于声辐射和纵向传递力，采用转子0.7R处施加等效激励力可以有效地反映转子表面分布式脉动激励力作用下的特征，并且幅值相差不大；对于横向和垂向传递力，采用转子0.7R处施加等效激励力在特征和响应幅值上将产生较大的差别。

(4) 对于声辐射和各向传递力，在转子桨毂处施加等效激励力在特征和响应幅值上将产生重大的差别。