二阶非对称双螺杆挤出机三维仿真
2021-06-04郭树国王丽艳
于 淼 郭树国 王丽艳
(沈阳化工大学机械与动力工程学院,辽宁 沈阳 110142)
近年来,人们对蛋白质的需求量日益增加,但由于大豆种植面积减少,造成了较大的大豆蛋白缺口[1]。郭树国等[2-3]研究发现,可以利用挤压膨化技术对大豆的高蛋白副产品——豆粕进行加工。但是作为豆粕的主要加工设备——传统的双螺杆挤出机的挤出性能已不能满足行业发展的需要[4]。而螺杆作为双螺杆挤出机的重要组成部分,其构型是影响挤出机性能的重要因素[5-6],因此需对螺杆构型进行改进。
梁振刚等[7-8]提出了阶梯状双螺杆挤出机构,其后一阶螺槽容积小于前一阶的,因此具有良好的物料压缩能力。喻慧文等[9]提出了具有自洁功能的非对称同向双螺杆挤出机,由于两根螺杆的转速与螺纹形状不同,会产生非对称流场以及速度的周期性变化,使得差速双螺杆挤出机具有良好的分散混合能力。但上述研究只对挤出机的某一性能进行了改进。文章拟以二阶差速双螺杆挤出机为试验对象,以黏性流体力学为理论依据[10-11],以ANSYS/CFX有限元分析软件为平台[12],近似模拟物料的运动情况并进行分析,旨在为双螺杆挤出机的设计提供依据。
1 模型及参数
1.1 几何模型
二阶非对称双螺杆挤出机为四段螺杆,其几何参数如表1所示。每根螺杆通过高40 mm,底圆直径30 mm,上圆直径35 mm的带有混炼元件的圆台连接,中心距46 mm,机筒厚2 mm,与螺杆间距1 mm。
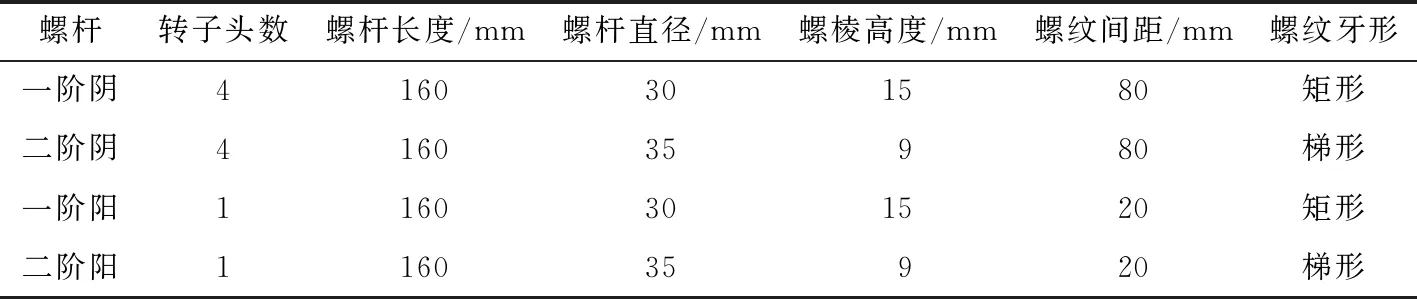
表1 四段螺杆几何参数Table 1 Geometric parameters of four section screw
根据四段螺杆几何参数,使用Solidworks软件建立二阶差速双螺杆挤出机的三维实体模型(图1)。

图1 二阶差速双螺杆挤出机三维模型Figure 1 Solid model of second order differential twin screw extruder
1.2 数学模型
为了便于流场模拟分析,选择密度为2 112 kg/m3,黏度为1 930 Pa·s,恒定温度为80 ℃的不可压缩幂律流体豆粕作为试验材料[13],并对流场作出以下假设[14-15]:流体在流道内作层流运动且完全充满流道,流场为恒温,机筒内壁与螺杆表面无滑移;同时忽略流体的惯性力、重力等体积力,根据以上假设得到简化后的数学模型[16]。
(1) 连续介质方程:
(1)
式中:
Vx、Vy、Vz——x、y、z方向上的速度矢量,m/s。
(2) 运动方程:X、Y、Z方向的运动方程如式(2)~式(4) 所示。
(2)
(3)
(4)
式中:
P——静压力,Pa;
τij——直角坐标系下剪切应力分量(其中i、j分别为x、y、z)。
(3) 本构方程:
(5)
式中:
m——物料黏度,Pa·s;
ϒ——剪切速率,s-1;
n——幂律指数。
2 二阶非对称双螺杆挤出机流场数值模拟
2.1 有限元模型建立
将Solidworks软件建立的模型导入ANSYS中,利用建模工具Geometry对挤出机模型进行填充、布尔求差等操作,获得挤出机的流场模型。将流场模型导入mesh中进行四面体网格划分(见图2),通过网格划分产生106 680个节点,491 209个单元。

图2 网格划分后的流场模型Figure 2 Flow field model after mesh generation
2.2 边界条件
根据实际工作情况以及对流场的假设给出边界条件:
(1) 由于设置速度入口与压力出口使计算收敛最稳健,经多次调试,故设置进口面速度为0.05 m/s,出口面压力为0.5 MPa。
(2) 通过对不同转速进行实验验证,当阳转子转速为120 r/min,阴转子转速为60 r/min时,模拟数据与测试数据的误差最小。故设置阴转子螺杆的转速为60 r/min,阳转子螺杆的转速为120 r/min,换算为角速度分别为6.28,12.56 rad/s。该模型以阴转子连接圆台底圆的圆心为原点,则阴阳转子表面的速度公式分别为[17]:
(6)
(7)
实际生产中,由于机筒是静止的,机筒速度设置为0,故机筒内表面速度为0。
2.3 结果与分析
2.3.1 压力场 由图3可知,压力沿挤出方向逐渐增大,符合实际生产条件。第二阶螺杆的压力大于第一阶螺杆且二阶螺杆的建压能力优于一阶螺杆,故第二阶双螺杆具有较好的压缩能力。同时,压力在混炼过渡段存在不规则变化,使这一区域物料的回流量增大,提高了挤出机的分布混合性能。

图3 流场压力云图Figure 3 Global macro pressure nephogram of flow field
由图4可知,ZY平面同一直线上的下啮合区压力大于上啮合区,是由于左右两根螺杆之间存在不同的导程与转速造成的。啮合区压力呈相互交错分布,物料在啮合区被不断地拉伸与压缩,有利于物料的充分混合。
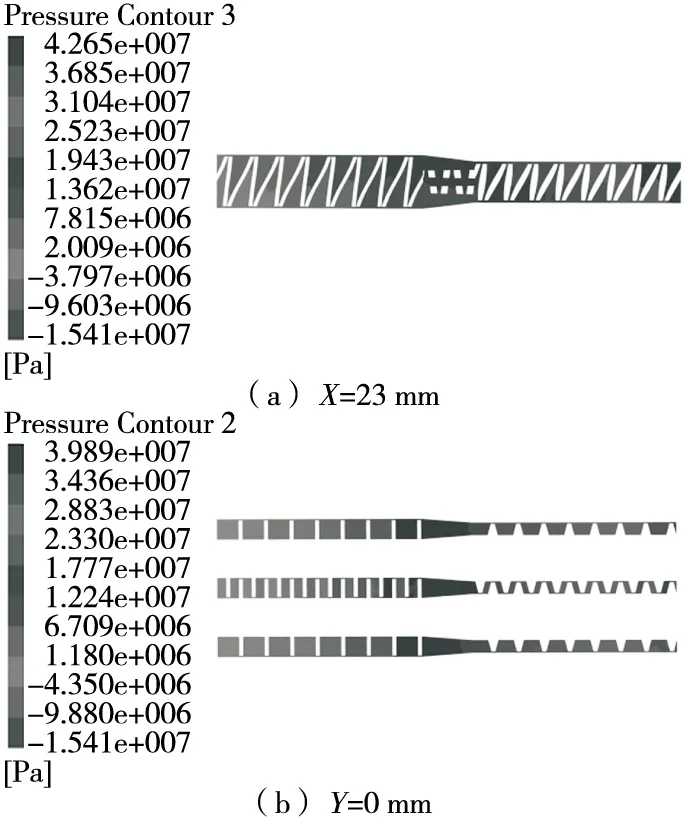
图4 轴向压力分布云图Figure 4 Axial pressure distribution of different sections
2.3.2 速度 由图5可知,阳转子螺槽处的物料流动速度大于阴转子螺槽处的,与给定的工况条件相符。由于阳转子与阴转子的旋转方向相反且存在速度差,因此啮合区物料出现最大速度,啮合区产生大的剪切速率,有利于物料的剪切分散,故物料在啮合区能够充分混合。同时,物料经混炼过渡段时,整体速度减小,物料在该段停留时间增长,有利于物料的混合。

图5 新型双螺杆的速度矢量图Figure 5 Velocity vector diagram of a new type of twin screw
由图6可知,物料在阳转子螺槽中的分布比阴转子螺槽中更加分散,说明阳转子混合性能优于阴转子。混炼过渡段,物料经螺棱螺槽时流线被切割,在此区域后的螺槽中流线又再次进行重新组合,且这一过程具有周期性,因此物料在混炼过渡区经历多次的分割、重组,物料混合得更充分,提高了挤出机的分散混合能力。

图6 新型双螺杆的流体迹线图Figure 6 Fluid trace diagram of a new type of twin screw
由图7可知,同一截面上的不同位置存在速度差,Z=-70 mm截面上的速度差大于Z=30 mm截面上的,而大的速度差产生大的剪切速率,有利于物料的剪切分散。同时,Z=-70 mm截面上的速度震荡更为剧烈,更有利于物料的混合。因此,二阶段的分散混合性能优于一阶段。
Z=-20 mm截面上的整体速度小于其他两个截面,但由于混炼元件的存在,物料在螺棱螺槽时的速度达到最大,使得这一截面的速度差大于其他两个截面,说明混炼过渡段的剪切能力强,有利于物料的充分混合。
由图8可知,由于混炼元件的存在,剪切速率在进入混炼过渡段时迅速增大,且剪切速率大小为混炼过渡区>二阶段>一阶段,与图7的结论一致。

图7 轴向不同截面的速度分布Figure 7 Velocity distribution of different axial sections
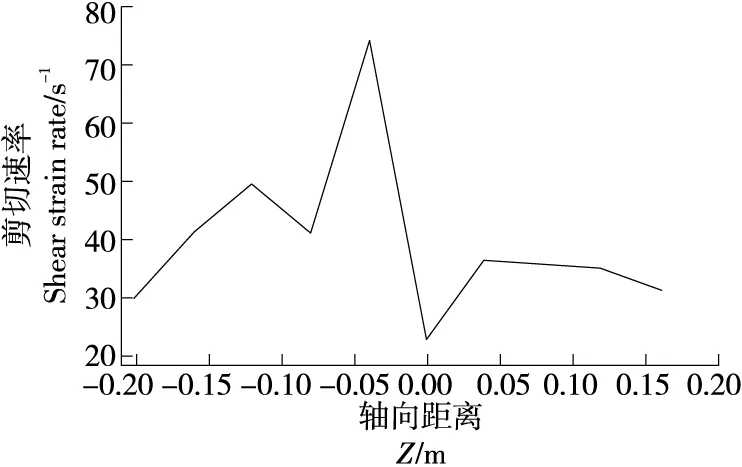
图8 啮合区的剪切速率场Figure 8 Shear rate fieid in the meshing region
3 样机实验验证
为了验证模拟结果的可靠性,对二阶非对称双螺杆挤出机进行生产试验,以低温豆粕作为填充物料,阳转子转速分别为100,110,120,130,140,150 rad/min下,测量流体进出口处压力,并将其代入有限元模型中得到挤出质量流。
由图9可知,模拟数值与测量值之间具有相似的线性关系,变化趋势一致。同时,两者的数值结果相近,最大误差仅为9%,故建立的几何模型与物理模型相符,仿真结果可靠。

图9 新型双螺杆挤出机挤出质量流与螺杆转速的关系Figure 9 Relationship between extrusion mass flow and screw speed
4 结论
使用CFX对带有混炼元件的二阶非对称双螺杆挤出机进行数值模拟与分析。结果表明:当流场温度为80 ℃ 时,由于差速非对称流场、混炼元件以及一、二阶段螺槽存在容积差,增强了挤出机的剪切能力、延长了物料的停留时间,使二阶非对称双螺杆挤出机具有较好的压缩能力和分散混合性能。后续可对其他双螺杆挤出机进行数值模拟,并与其进行对比分析。
