深切峡谷相邻桥址区风速相关性研究
2021-06-04余佳昕张明金李永乐
余佳昕,张明金,李永乐
(西南交通大学桥梁工程系,四川成都 610031)
近年来我国为了发展西部经济进行了大量的基础设施建设,其中不乏位于高山峡谷间的超大跨桥梁,但由于山区复杂的风场分布特性,存在湍流强度大和风切变强烈的特点[1],在设计山区桥梁时,为了确定桥梁的设计基准风速,通常采用数值模拟的方法模拟风环境,无需花费大量成本测量现场风速。
数值模拟是目前主要的风特性分析方法,数值模拟主要通过计算流体力学为基础,可以以极低的成本模拟山区风环境,另外两种方法为:风洞试验和现场实测[2]。目前数值模拟主要针对,湍流模型,边界条件,和特殊风场分析。对于湍流模型,主要针对不同地形条件下不同的湍流模型的适用性研究。Uchida和Ohya[3]研究了大涡模拟在风特性模拟中的应用,并取得复杂地形的风特性数据。Xiao[4]等将多种不同的湍流模型应用于一个范围10.1 km×6.9 km的小岛区域,分析不同湍流模型下的小岛的风场分布。
对于边界条件近年来主要针对于入口风速模拟。研究多尺度分析的耦合是模拟边界层的高雷洛数和复杂流动现象的潜在方法[5]。沈炼[6]等结合WRF中尺度气向分析为小尺度的CFD分析模拟边界湍流入口,这种耦合方式能较好的模拟风场内的湍流强度。
复杂风场分析现被用于为复杂地区桥址区选址和设计风速确定提供参考。李永乐[7]等基于Y型河口研究了其风特性分布情况,研究了不同于普通深切峡谷的风特性。张玥[8]等基于一斜拉桥实际工程,利用多年的现场实测和数值模拟相结合的方式验证桥址区风环境,并应用于桥梁风振研究中。遆子龙[9]等基于FLUENT研究了不同地表粗糙度对桥址区风环境的影响,研究发现增加地表粗糙度可能使主梁处风速增加。王云飞[10]等通过数值模拟研究了山区大坝对风环境的影响,发现大坝削弱了桥址区的风速和正攻角效应。
以上研究重点针对于模拟方法和特定地形条件下的风场模拟,对于两桥之间的风速相关性研究较为缺乏。本研究基于西南山区大渡河上两座距离仅4.88 km的千米级大跨桥梁,且桥轴线基本平行,相差不超过2 °。一座为川藏公路大渡河大桥,另一座为川藏铁路大渡河大桥,研究系统研究了两桥在不用入口风向下的风速相关性。
1 数值分析模型
1.1 工程概况
两桥位于西南山区的深切峡谷之中,分别位于泸定县城上下游。两桥址区峡谷高差达5 000 m,地形和地表状态复杂,是典型的青藏高原深切峡谷,受南亚季风和青藏高原的双重影响,可能存在较强的局地风场。两座千米级大跨桥梁相距仅4.88 km,均为川藏线控制工程。公路桥东南侧存在一条海拔约2 000 m的高耸山脊,铁路桥西侧有一突出山体,高程约为2 320 m。两桥轴线基本保持平行,桥位设定角差不超过2 °。桥位布置见图1,立面布置见图2。

图1 桥位布置平面
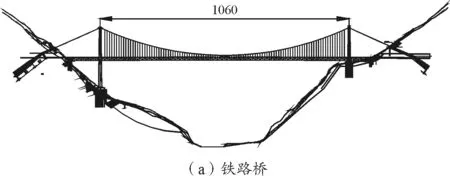
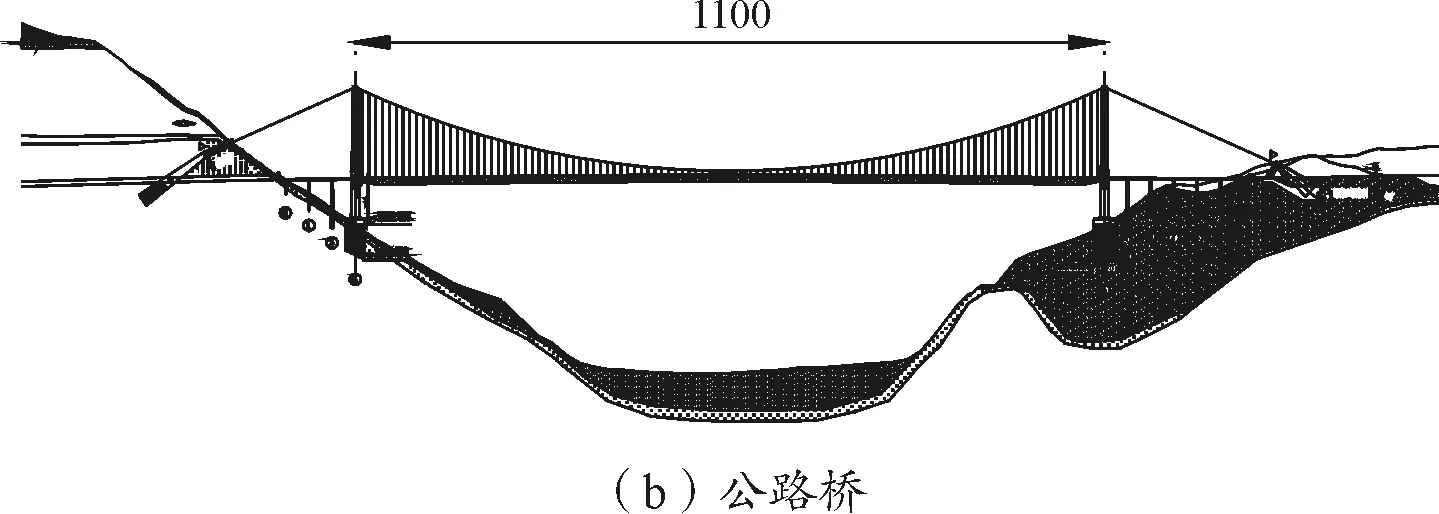
图2 桥位布置立面(单位:m)
1.2 模型建立
根据该地的地貌特征地形范围取为20 km×20 km,以此保证风场的充分发展,地形模型的下表面为山体与河流,顶部高程取为10 000 m。采用6面体网格对计算区域进行离散划分,为了能在保证计算效率的前提下增加桥址区模拟精度,网格采取了从两侧向桥址区处逐渐加密网格,形成两侧网格较为稀疏,中间网格划分较密的网格计算区域。底层壁面网格高度为2 m,并采用较低的网格增长率,充分模拟桥址区域的风场,最终形成了网格数量为380万的计算区域。网格划分见图3。

图3 三维地形模型及网格划分
计算湍流模型使用SST k-ε模型,压力与速度耦合采用SIMPLEC算法,离散格式选用二阶精度格式。模型的底部边界为WALL边界,顶部边界为对称边界,前后左右四个边界根据工况的不同,选为压力出口或速度入口。
风场计算中入口处来流风速分布偏安全地采用气象观测站标准场地对应的风剖面,边界层高度取为1 640 m,边界层的海拔高度为3 000 m。计算入口风速通过用户自定义函数(UDF)进行设置,高程3 000 m以上部分风速取为50 m/s,高程3 000 m以下部分按B类地表(标准场地)风速随高度变化的指数规律进行设置,高程1 360 m处为入口处谷底,其中梯度风速取为50 m/s,梯度风高度取为1 640 m。入口处风速可用下式表示,风速分布如图4所示。
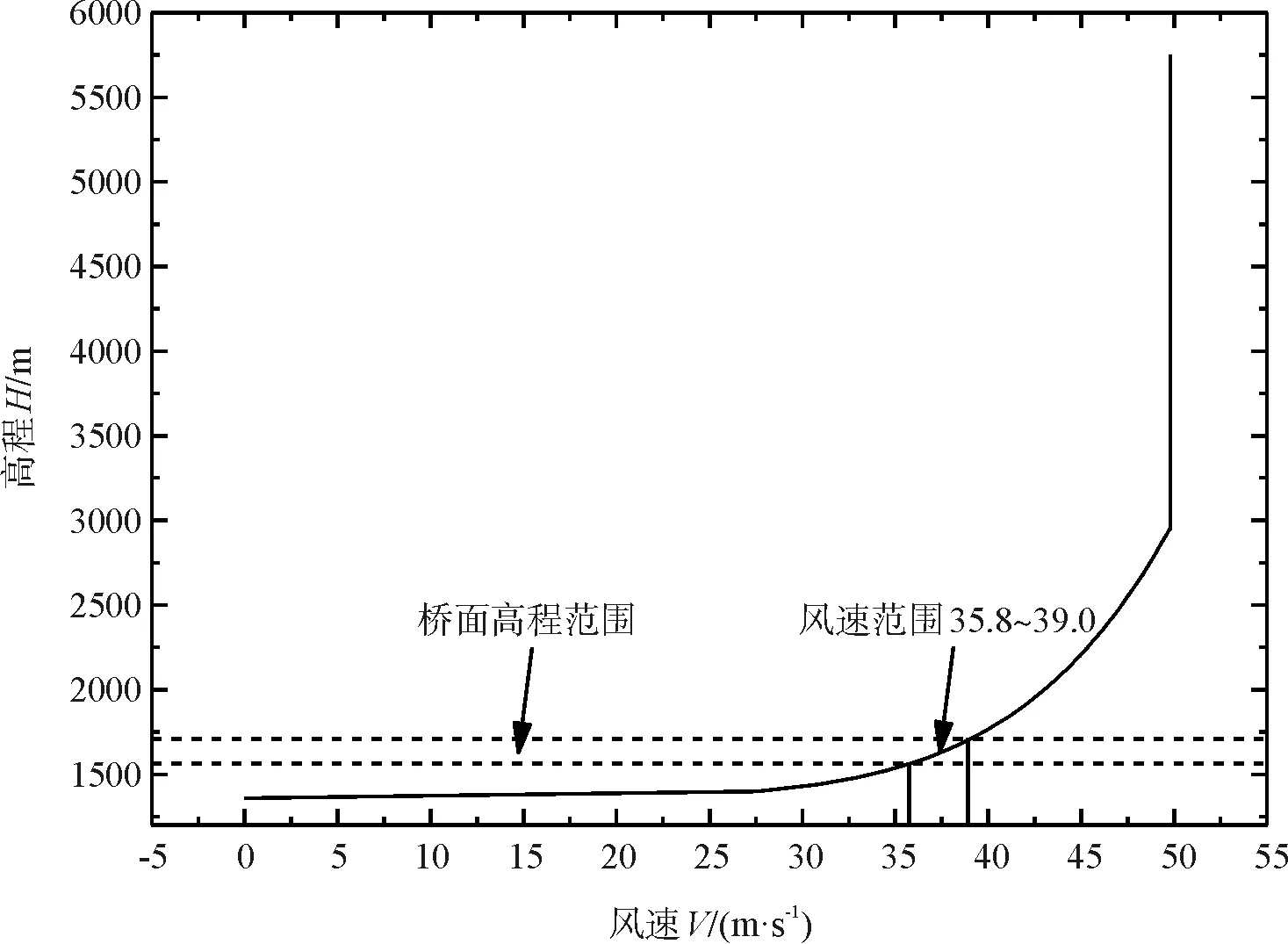
图4 入口边界风速剖面
1.3 计算工况与观测点设置
泸定县50 a历史风向资料表明桥址区风向主要为南北向。为考察不同方向来流对桥位风场的影响,计算中入口来流取24个方向(如图5所示),图中数字代表计算工况号,其中以南偏西15.9 °方向(工况13)为来流垂直于桥位桥轴线的入口风,其余工况以南偏西35.9 °方向(工况11)为始,逆时针每10 °一个工况,共11个工况。同样在桥轴线的对应侧也有相应的11个工况,此外设置两个与河道走向基本垂直的工况(工况10与工况22)。为了方便讨论以风向与南北轴线的夹角代替各工况的名称,其中由南向北逆时针为正,顺时针为负,风攻角以向上为正,向下为负。
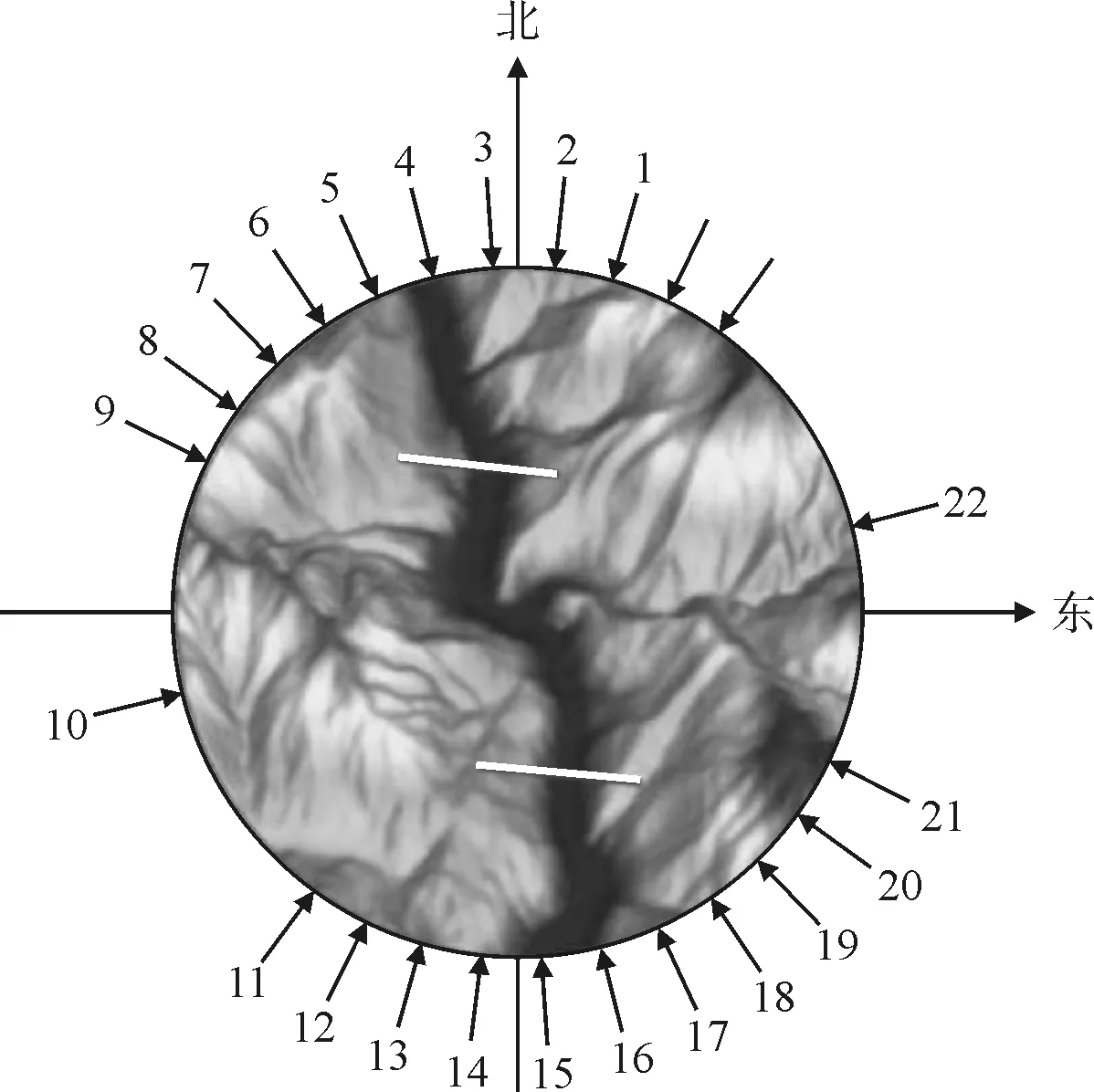
图5 风向工况示意
为获取桥位关键点的风速情况,在两桥塔间每1/8跨布置一个检测点,桥轴向上共设置九个监测点,为了更好地捕捉桥位处的风速剖面情况,在近桥面高度附近进行了加密。在铁路桥址区桥面下布置15个检测点,桥面以上布置10个检测点,共25个检测点。在公路桥址区,以同样的布置原则,在桥面以下布置12个检测点,桥面以上布置13个检测点,共25个监测点。故两桥址区总共设置66个监测点(图6)。
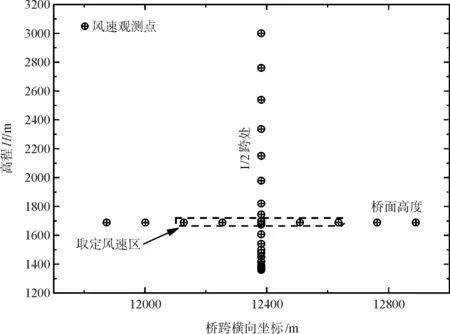
图6 两个桥位观测点位置示意
2 计算结果与分析
2.1 跨中和桥塔风速
图7(a)和图7(b)为不同入口风向下公路桥和铁路桥的桥面跨中和桥塔处的横桥向风速。从图中可以看出,桥面跨中和桥塔处风速展现出了高度相似的变化规律,这表明跨中处的风速和桥塔跨中处的风速存在较强的相关性,整体上看公路桥风速由于东侧山脊线的影响风速在一定范围内呈现出较大起伏,但桥塔和跨中处风速依然保持一致性良好的风速变化规律。由于铁路桥位于峡谷中段,风环境相对稳定,从图上表现出比公路桥更好的拟合性。
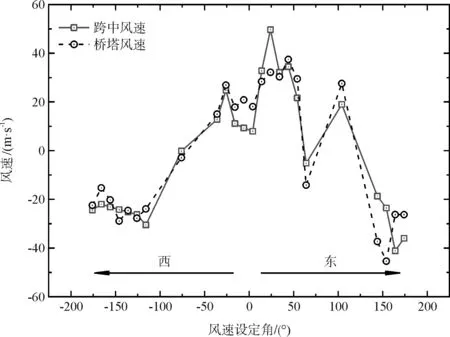
(a)公路桥风速

(b)铁路桥风速图7 跨中风速与桥塔风速
图8(a)和图8(b)为两桥跨中和桥塔处横桥向风速线性回归拟合。将从图8上可以看出,两桥的桥塔和跨中风速均表现出了较好的风速线性相关性,其中公路桥的拟合风速的截距为0,斜率为0.96。铁路桥的截距为0,斜率为0.99。可以看出风环境相对稳定的铁路桥比公路桥风速更接近1。主要是由于公路桥的桥址区相比铁路桥明显复杂,四周存在多座高耸山体的影响,使公路桥的风速较为发散。
2.2 两桥位跨中风速相关性
下图9为两桥跨中横桥向风速,从图9可以看出,两桥在不同入口风向下跨中横桥向风速变化规律存在一定的相似性,这说明两桥的横桥向风速存在着一定的相关性。但从图上也能发现,在个别工况下,两桥的横桥向风速存在较大差异,这来源于公路桥四周的高耸山脊线和山体对风场的影响,且差异风向主要为风偏角较大工况21和工况22。从图9可以看出,西侧来流作用下,两桥的横桥向风速一致性较好,东侧来流时,由于高耸山体的影响,两桥的风速出现了较大的差异。由此可以看出,在没有特殊山体的影响下,由于峡谷河道对气流导向作用使得同一河道紧邻的上下游桥梁的跨中横桥向风速存在这较强的风速相关性。

(a)公路桥风速拟合

(b)铁路桥风速拟合图8 同一座大桥跨中和桥塔处风速线性拟合
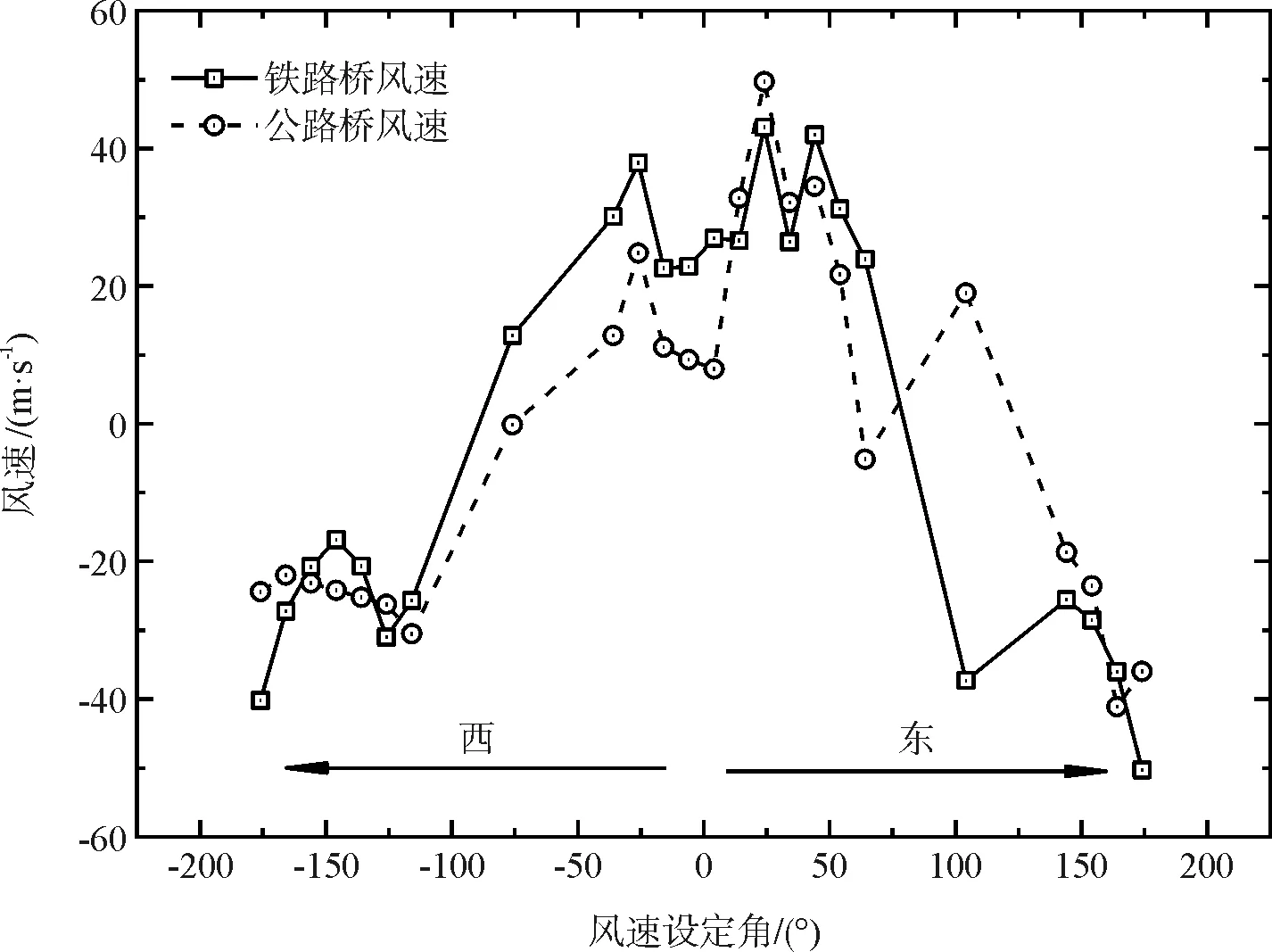
图9 两桥位跨中横桥向风速
为了更好地研究两桥横桥向风速的相关性,将两桥不同工况下的桥面的横桥向风速进行线性拟合,如图10所示,其中不考虑个别受山体遮挡的工况,从图上可以看出,在不考虑个别特殊工况的情况下,两桥的横桥向风速具有较好的线性相关性,在截距为0的情况下拟合风速斜线的斜率为0.823。表明紧邻的上下游桥梁的横桥向风速有较好的线性相关性。
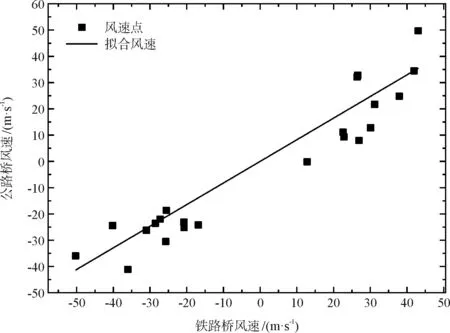
图10 两桥位跨中横桥向风速相关性
2.3 两桥位桥塔风速相关性
为了研究两桥的桥塔处的风速相关性,下图11给出了两桥的西侧桥塔的不同工况下的横桥向风速和两桥的横桥向风速比值。可以从图上看出,不同的入口风向作用下,除个别工况外两桥的桥塔处横桥向风速变化规律基本相同,但相比跨中稍差。整体上依然表现出西侧来风的规律性相比东侧来风更好的特点,这主要是由于西侧桥塔受东侧山脊线的影响较小。从跨中和西侧桥塔在西侧来风作用的下的变化规律可以看出两桥的变化规律是基本一致的。总体上看风速与河道夹角较小时,两桥的桥塔处风速相关性更好。
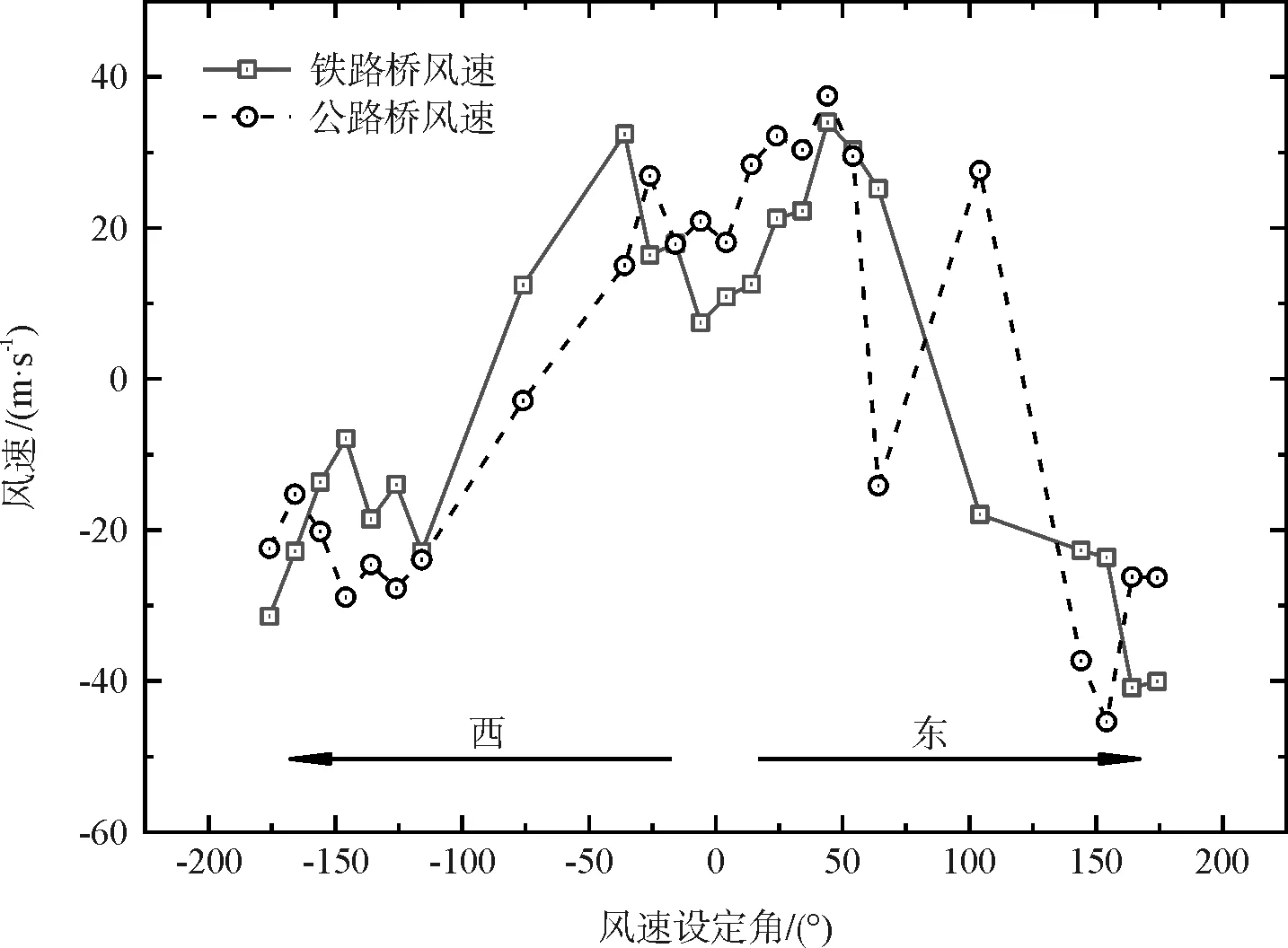
图11 两桥西部桥塔横桥向风速
如图12所示,将两桥的西侧桥塔处风速进行线性回归拟合,两桥西侧桥塔的横桥向风速比较符合线性相关性相较于跨中较弱,风速点更为离散。图中的拟合风速线截距为0,斜率为0.8736,由此可以看出同一峡谷中的紧邻的上下游桥梁在靠近两侧山体的桥塔处的风速依然具有相关性,但弱于跨中。
3 结论
通过建立考虑临近山体的三维风场数值分析模型,研究了复杂山区突出山体影响下两座相临桥梁桥址区风速相关性,得到以下结论:
(1)在同一桥址区中的桥塔和跨中的风速相关性良好,整体上风速变化规律相同,特别是当入口风向与河道夹角较小时,表现出了良好的线性相关性。
(2)对于上下游桥梁跨中的相关性,可以看出,由于山脊线的影响在公路桥跨中受明显遮蔽时,两桥表现出风速明显差异,由此看出,当桥梁受到高耸山体明显遮蔽时两桥的风速相差较大且规律不同,当山体的遮蔽效应降低后,两桥风速表现出较好的风速相关性。

图12 两桥位西部桥塔横桥向风速相关性
(3)对于上下游桥梁的西侧桥塔之间的相关性由于受两处桥址区的峡谷宽度和山体坡度的影响,两桥除特殊工况外的风速变化规律基本相同,但相关性弱于跨中。
