大流量低扬程水泵无叶区非定常流动特性研究
2021-06-03管子武何海平林方舟刘德民
管子武,何海平,林方舟,刘德民
(东方电气集团东方电机有限公司,四川 德阳 618000)
随着国家粤港澳大湾区战略的启动,珠江三角洲将面临人口大量增长和经济再次腾飞的双重利好。然而,该区水资源分布和开发严重不平衡:东部区域人口众多而水资源匮乏;西部人口少而水资源丰富。这将制约大湾区的发展。为此,水利部和广东省委省政府提出了珠江三角洲水资源配置工程,即从珠江三角洲网西部的西江水系向东引水至东部,向广州市南沙区、深圳市和东莞市等缺水地区供水。鲤鱼洲加压泵站和高新沙加压泵站是珠江三角洲水资源配置工程的核心。这两泵站具有流量大(鲤鱼洲泵站单机流量不小于13.5 m3/s,高新沙单机流量不小于15 m3/s)、扬程低和变幅大,以及年利用小时数高(全年运行时间不低于6 000 h)等特点。泵站的这些特点,决定了设计人员在产品开发时,必须注重其稳定性特性。很显然,非定常流动是影响稳定性的主要因素,特别是无叶区的非定常流动。在鲤鱼洲和高新沙泵站的招标文件中,业主对无叶区的压力脉动就有明确的要求。
无叶区的非定常流动特性受多种因素影响,但最主要的影响因素是动静干涉效应。针对动静干涉问题,在水轮机(水泵水轮机)和水泵领域都有非常多的工作[1-9]。所谓动静干涉是指转动部件(转轮)和静止部件(导叶)之间流动的相互干扰。对于水轮机,转轮叶片随着转轮转动,其头部周期性切割导叶出口尾迹区,影响尾迹区的流动特性;对于水泵,转轮叶片尾迹区随转轮选择,周期性撞击导叶,产生动静干涉效应。因此,在静止坐标系下监测无叶区压力脉动,则其主要频率为叶片通过频率及其倍频。前人的许多研究工作,包括理论分析[2-6]、数值计算[5-8]、模型试验[9]和真机监测[7],都印证了该结论。东方电机在水泵水轮机和水轮机方面,也开展了非常多的非定常流动计算研究工作[10-12]。这些经验为大流量泵的非定常流动特性研究提供了思路。
1 数值计算模型
1.1 计算物理模型
东电电机开发的大流量低扬程泵主要过流部件包括进口段、转轮(叶轮)、导叶和蜗壳等4部分。由于进口段的主要作用是为转轮进口提供均匀来流条件,其流态非常好。因此,在研究非定常流动特性时,为节省时间和计算成本,将不考虑进口段的影响情况。因此,本文研究的过流部件只包括转轮、导叶和蜗壳3个部分,如图1所示。其中,转轮的叶片数为7,导叶的叶片数为15。
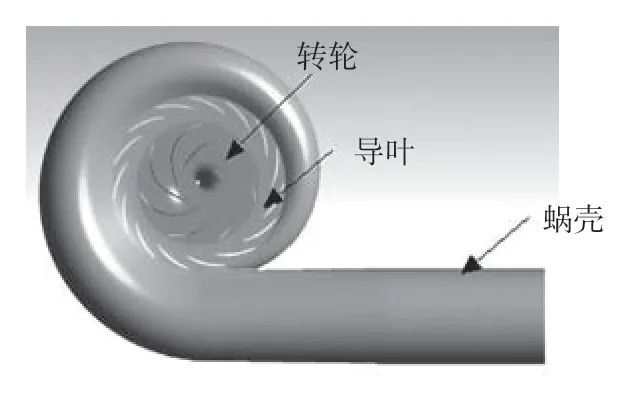
图1 大流量泵计算物理模型
蜗壳、导叶和转轮的网格如图2所示,其中,蜗壳采用非结构化网格,转轮和导叶采用结构化网格,网格数见表1。

图2 过流部件网格

表1 网格数
1.2 计算方法和边界条件
对于不可压缩流体,控制方程为:
连续性方程:

动量方程为:

本文采用Ansys CFX进行三维全流道非定常计算,采用二方程模型的SST湍流模型[13]来封闭控制方程组。
进口采用Opening边界条件,出口采用质量流边界条件,固壁采用无滑移边界条件;动静交接面采用Transient Rotor Stator方法。
时间项采用一阶离散格式,对流项采用迎风离散格式,湍流项采用一阶离散格式;内迭代收敛精度为10-5,转轮旋转1°计算一步。待计算稳定后,选取最后5个旋转周期数据作为分析对象。
压力脉动监测点位于Z=0平面、转轮-导叶动静交界面靠导叶侧,总共布置了4个监测点,即在圆周方向每间隔90°布置一个压力脉动监测点,如图3所示。

图3 压力脉动监测点布置图
2 计算结果及讨论
本文选取了最优工况和大流量工况点(Q=1.25Qopt,Qopt为最优点的流量)两个工况点进行非定常计算。
2.1 频谱特性
2.1.1 最优工况
图4是5个旋转周期内,无叶区4个测点的压力随时间变化情况,横坐标中T表示旋转周期,纵坐标中Popt=ρgHopt,Hopt为设计扬程。从中可以看出,压力变化规律性非常好。其中,靠近蜗壳的测点+VX压力均值最大,+VY的压力均值最小,而-VX和-VY的均值相对较小。
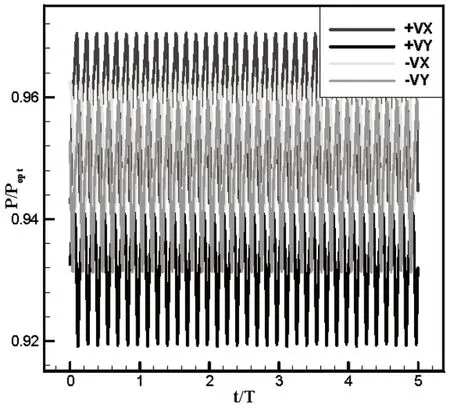
图4 最优工况压力随时间变化图
图5是压力脉动随时间变化情况,为显示方便,只展示0.4个旋转周期,纵坐标为压力相对幅值。从中可以看出,最优工况点压力脉动峰峰值小于4%。从中清楚地看到,压力幅值变化规律性非常好。+VX和-VY的压力脉动幅值稍大,+VY和-VX相对小一些。

图5 最优工况压力脉动随时间变化图

图6 +VY的频谱特性
图6是+VY特征频率,其中,fn为转轮转动频率。从中可以看出,第一主频是7倍转频,第二主频是14倍转频。其他几个监测点的频谱特性与+VY相同,其前三阶的分频幅值见表2。由此可见,无叶区压力脉动主要受动静干涉影响,其主要频率是叶片通过频率及其倍频。从表2中也可看出,+VX和-VY的压力脉动幅值比+VY和-VX的大。

表2 最优工况4个监测点压力脉动前三阶主频幅值
2.1.2 大流量工况
图7是5个旋转周期内,无叶区4个测点的压力随时间变化情况,其中纵坐标中Pq=ρgHq,Hq为当前工况扬程。从中可以看出,压力变化规律性非常好。与最优工况不同,大流量工况测点+VY的压力均值最大,+VX压力均值次之,而-VX和-VY的均值最小。

图7 大流量工况压力随时间变化图
图8是压力脉动随时间变化情况,也只展示了0.4个旋转周期。大流量工况点压力脉动峰峰值小于7%。从中清楚地看到,压力幅值变化规律性也比较好。+VX和-VY的压力脉动幅值稍大,+VY和-VX相对小一些。
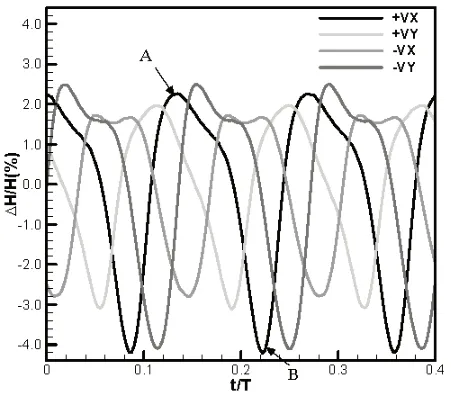
图8 最优工况压力脉动随时间变化图

图9 -VX的频谱特性
图9是-VX特征频率。从中可以看出,第一主频是7倍转频,第二主频是14倍转频。其他几个监测点的频谱特性与-VX相同,其前三阶的分频幅值见表3。由此可见,无叶区压力脉动主要受动静干涉影响,其主要频率是叶片通过频率及其倍频。从表3中也可看出,+VX和 -VY的压力脉动幅值比+VY和-VX的大。

表3 大流量工况4个监测点压力脉动前三阶主频幅值
2.1.3 与模型试验结果对比
本文的模型试验在DF-150水力试验台上进行。该试验台可进行反击式水力机械的水力性能试验,如水轮机、水泵水轮机、水泵等,项目包括能量、空化、压力脉动等试验。
图10(a)显示的是Q=0.98Qopt工况模型试验+VY压力脉动特性,图10(b)显示的是Q=1.26Qopt工况模型试验+VY压力脉动特性。从中可以看出,第一主频都是7倍转频。图10(c)显示的是模型试验压力脉动峰峰值和数值计算结果对比图,从中可以看出,计算的结果与模型试验结果非常接近。
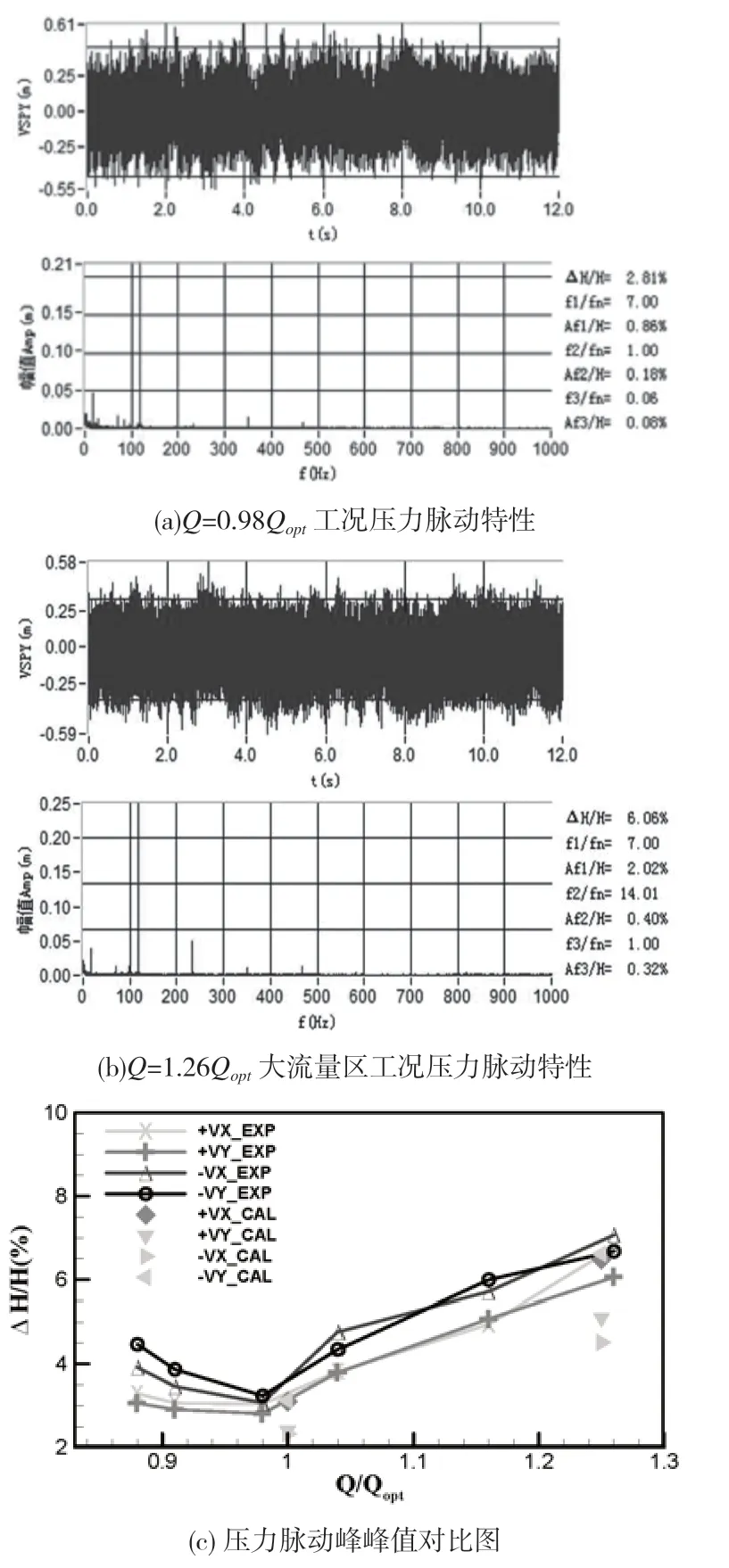
图10 计算的峰峰值与模型试验结果对比
2.2 流场特征
2.2.1 最优工况
本小节选取了两个时刻的流场进行考察,时刻A和B,见图5标识。

图11 最优工况A时刻(见图5)三维流线图
图11显示的是A时刻的三维流线图,从中可以看出,流线非常光滑,流态非常好。图12显示的是A时刻和B时刻无叶区Z=0平面的压力场的对比情况。图12中显示,靠近转轮叶片处,存在比较明显的低压区,这是叶片出口速度大的原因,如图13所示。事实上,在低压区附近还存在高压区,见后文图18。总体而言,无叶区的压力均值比导叶出口,即蜗壳内的压力均值小。随着叶片转动,低压区(高压区)也随着转动,从而产生叶片通过频率的压力脉动特征。

图12 A时刻和B时刻无叶区压力分布

图13 A时刻和B时刻无叶区二维流速分布
2.2.2 大流量工况
图14显示的是A时刻的三维流线图。从中可以看出,在导叶进口处,水流的冲击比较明显。除此之外,流线也比较光滑,流态较好。导叶进口端水流的冲角较大,水流冲击导叶压力面,造成该处压力大,见图15。图15又显示,无叶区的压力均值都比较高,比导叶出口的压力均值大。这点与最优工况的现象相反。因此,无叶区的压力受到转轮叶片和导叶的共同作用。图16显示的是流速分布,从中并未发现脱流现象。

图14 大流量工况A时刻(见图8)三维流线图

图15 A时刻和B时刻无叶区压力分布

图16 A时刻和B时刻无叶区二维流速分布
2.3 讨论
上文介绍了最优工况和大流量工况无叶区压力脉动情况。通过对比,可以发现这两个工况的压力脉动有所区别,最明显的见图5和图8 -VX监测点的图形。最优工况,-VX监测点压力从波峰到波谷基本上是单调的,波谷到波峰也是单调的;而大流量工况,-VX存在两个波峰。如何解释流量变大,压力脉动出现两个波峰的现象?
本文选择无叶区某一等半径的截面作为考察对象(R=0.52D1,其中D1为转轮出口直径),分析该处平均速度和平均压力(转轴方向平均)沿周向的分布情况。图17为速度分布,图18为压力分布,其中P=P/(ρgHq)是无量纲压力,Hq分别为设计扬程和1.25Qopt工况对应的扬程。从图17可以看出,对于最优工况,速度从波峰到波谷和波谷到波峰的变化单调性都非常好(除红圈附近外,即隔舌附近);对于大流量工况速度从波峰到波谷单调性比较好,而波谷到波峰的单调性在黑圈附近受到了破坏,因此流动更为复杂。可以推测,随着流量继续增加,流速分布将更为复杂,无叶区将出现脱流现象。因此,对应的压力分布规律就更为复杂。

图17 转轮出口流速分布
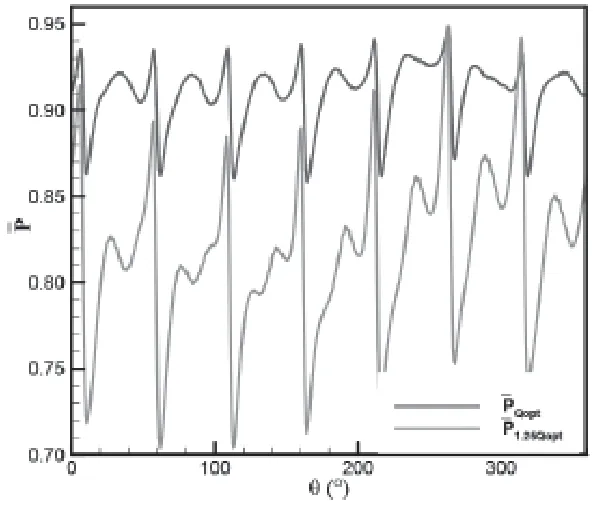
图18 转轮出口压力分布
3 结论
本文通过三维CFD计算,研究了大流量低扬程泵无叶区的非定常流动特性,得到结论如下:
(1)通过与模型试验结果对比,说明了本文数值计算的可靠性。
(2)无叶区压力脉动幅值较小,最优工况小于4%,大流量工况小于7%;频率为叶片通过频率(7倍转频)及其倍频。
(3)最优工况点,流场均匀,流态非常好,因此稳定性好,效率高;大流量工况,流态较为均匀,水流对导叶进口有一定的冲击,造成压力脉动幅值增加。
(4)大流量工况转轮出口流速沿周向分布比最优工况复杂,因此压力分布复杂,脉动增加。
