GPS高程测量数据处理分析及拟合方法研究

张建威，李 江

(1.河南能源化工集团 永煤公司车集煤矿，河南 永城 476600； 2.河南能源化工集团 永煤公司，河南 永城 476600)

20世纪70年代，美国首先建立了全球定位系统，世界各地开始对GPS定位技术开始研究，也逐渐扩展到利用GPS高程的测量中。20世纪80年代初，中国也开始对GPS技术进行研究，把GPS接收机应用于多个领域中。20世纪90年代，国内外学者对GPS高程测量数据处理分析及拟合方法进行了大量的研究。于素君[1]对石油物探GPS控制测量理论和方法进行了研究，以石油勘探中地震勘探测线的布设问题为主线，提出了一种基于稳健估计的曲面拟合法，分析了GPS数据及控制测量处理方法和符合物探施工精度要求的导线测量；刘俊领等[2]研究了GPS高程拟合方法，分析了GPS高程精度要求、拟合方法，经试验论证，GPS高程拟合的相应数学模型对地质高程的拟合具有一定的成效；解祥成等[3]分析了GPS拟合高程代替五等水准测量精度，分析了GPS高程转换的过程，研究了数学模型拟合法，并对某地区GPS水准高程和拟合高程的精度进行了对比分析，最后利用GPS观测值加已知高程点拟合，对待定点高程的求解方法进行了详细研究。

1 GPS水准测量的误差分析

1.1 误差源

GPS测量模式是影响GPS测量大地高精度的主要因素。为了减小误差，利用双频接收机、差分技术静态观测进行观测，其垂直精度和水平精度得到了明显的提高。但是，根据具体精度要求、设计经费和外部条件，需要对GPS的观测方法进行综合考虑。

GPS水准测量的误差来源主要是地面接收站、卫星信号传播站和GPS卫星。不同等级水准测量的精度可以用每千米高差中数的全中误差(MW)和偶然中误差(MΔ)。不同等级水准测量精度指标[4-5]见表1。

表1 不同等级水准测量精度指标Tab.1 Different levels of leveling accuracy indicators

当完成闭合环或附合线路测量时，如构成水准网的环数>20，应计算每公里高差中数的全中误差：

(1)

(2)

式中，N为水准环数目；F为水准环长度；W为各项改正后闭合差；R为测段长度；Δ为往返高差不符值。

1.2 提高测量精度的措施

由实践经验和理论分析可知，主要有以下提高测量精度的措施[6-9]。

(1)提高测定大地高的精度。①采取方法提高GPS网基线解算的坐标精度；②减弱对流层延迟误差和多路径误差；③当进行观测时，选择最佳的卫星部分；④选择最优的双频GPS接收机；⑤对GPS星历的精度进行改善。

(2)提高联测几何水准的精度。①当GPS网有特殊精度要求，采用二等精密水准进行联测；②当测量误差占GPS水准总误差的30%时，应采用三等几何水准进行联测。

(3)提高GPS水准计算精度。①采用抗差估计法，对计算数据中某点精度不高或粗差；②选择模型时，应优选对综合模型进行考虑；③选择已知点时，应选择具有代表性且均匀分布的测点。

2 模型参数的抗差估计

本文主要分析多项式拟合模型的抗差估计和模型参数的优选，先分析基于权阵迭代抗差估计的多项式模型参数的抗差估计。选择客观的权阵是获取估计值的保证，权阵表达式：

(3)

当GPS所测的大地高协方差设置为∑hh，则几何水准得到正常协方差阵为∑HH，则权阵的表达式：

P=∑-1=(∑hh+∑HH)-1

(4)

当把已知点的高程异常值ξ=h-H是高精度的，则初始权阵P，可根据已知点到待求点的已知距离来进行计算：

(5)

式中，e为一个较小的数；Di为已知点i到待求点的距离；C0为单位权值。

引入抗差估计方法的目的：避免粗差对模型参数估计产生不良影响。简单实用的迭代公式：

(6)

式中，n是最小二乘原则下迭代得到误差方程的次数。

测量数据处理中的权函数：

(1)丹麦法。表达式：

(7)

式中，C为常量，一般取值为3.0或2.5。

(2)Hubber方案。表达式：

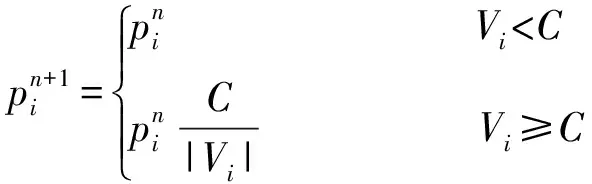
(8)

式中，C为常量，一般为2倍中误差。

(3)IGGⅢ方案。表达式：

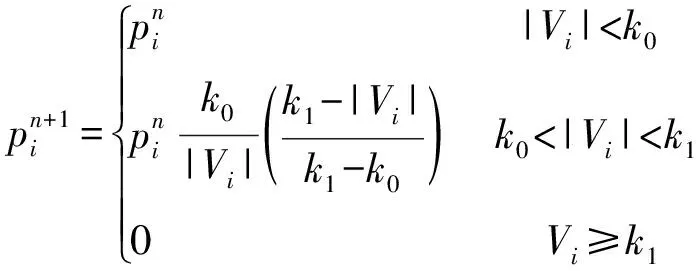
(9)

式中，k0为1.5倍的中误差；k1为2.5倍的中误差。

由式(7)—式(9)可知，通过不断迭代的解算误差方程，一般正常数据的权值比误差较大的已知数据的权值小，从而把粗差数据从已知数据中进行剔除。

3 GPS高程拟合模型的选择

3.1 拟合结果的精度评定

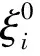
(10)

式中，n为参与计算的已知点。

(2)外符精度。GPS水准的外符精度M：

(11)

式中，n为参与检核的点数。

GPS高程转换模型参数优选流程如图1所示。

图1 GPS高程转换模型参数优选流程Fig.1 GPS elevation conversion model parameter optimization process

GPS水准相对精度评定方法：①闭合差检核；②相对误差检核。

假设检核点到已知点的距离为L，基于水准限差的检核点拟合残差的限值见表2，然后将限值和残差作比较，做GPS高程精度评定。

表2 基于水准限差的检核点拟合残差的限值Tab.2 Limit of fitting residuals based on level tolerance

3.2 AIC准则

AIC准则是由Akaike基于信息论的角度提出的，该准则树要用于模型的选择和顶阶上，从而获得理想的结果，采用AIC准则，对模型进行分析对比，得出模型的检核误差和内附误差，然后得到2个AIC值：AICc和AICi，两者相加得到AICt。最后对两者的信息进行比较，来确定模型的好坏。

AIC准则的表达式：

AIC=logσ2+(2m+3/n)

(12)

式中，n为代入计算值的个数；m为所选模型的参数，其中m≤n。

在GPS高程转换过程中，二次曲面模型时，m=6；三次曲面模型时，m=10；平面模型时，m=3。

4 应用实例

某测区整体较为平坦，测区长25.0 km，宽13.0 km，总面积为325.0 m2。测区有3个200～300 m的山包，测区共有27个水准联测点，选择11个检核点、16个拟合点。为了尽量减少点位之间的影响，选择16个拟合点均分布在测区中。测区测点点位分布如图2所示。

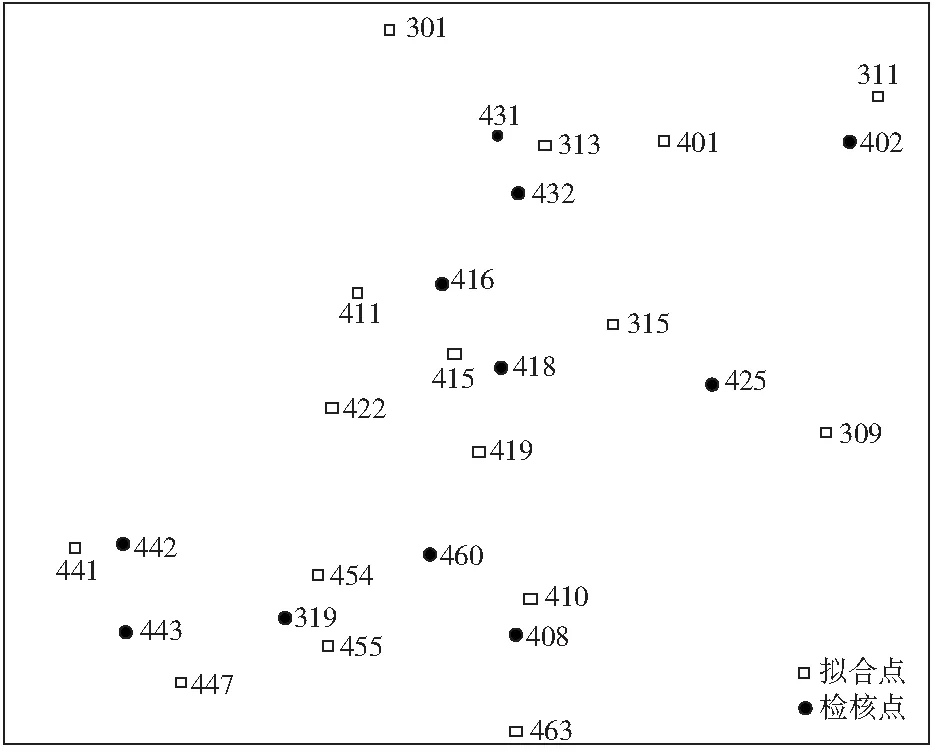
图2 测区测点点位分布Fig.2 Point distribution of measurement points

当测量数据进行粗差剔除后，采用混合模拟模型、综合拟合模型、多面函数拟合模型、三次曲面拟合、二次曲面拟合，对水准联测数据进行检验和拟合，其检验和拟合的结果见表3。

表3 不同模型对水准联测数据进行检验和拟合结果Tab.3 Different models test and fit joint level test data

由表3可知：

(1)检核点的高程异常大于拟合点，说明该拟合模型是根据拟合点高程异常数据组建的。

(2)混合模型和综合模型的拟合精度要明显优于单一模型(多面函数、三次函数、二次函数)的拟合效果。

(3)在11个检核点中，有2个点的拟合精度较高，分别为319检核点、418检核点；在17个拟合点中，有3个点的拟合精度较高，分别为313拟合点、410拟合点、415拟合点，根据这5个点的分布情况，该5个点位于水准联测点相对密集的位置，表明增加水准联测点，有助于提高拟合精度。

为了清晰地对各个模型的模拟结果进行比较，采用AIC准则，验证模型的有效性，分别对5种模型拟合结果的AIC值、最小值、最大值和标准值进行计算。实例中模型的精度和AIC值见表4。

由表4可知：根据最小值、最大值、标准差分析，综合模型和混合模型的模型精度优于单一模型，其AIC值也明显高于单一模型，表明，采用AIC准则优于对模型的优劣进行评判。

表4 实例中模型的精度和AIC值Tab.4 Accuracy and AIC value of the model in the example

5 结论

通过GPS水准测量的误差分析、模型参数的抗差估计、GPS高程拟合模型的选择以及现场应用，分析了GPS高程测量数据流程，然后分别以混合模拟模型、综合拟合模型、多面函数拟合模型、三次曲面拟合、二次曲面拟合对水准联测数据进行检验和拟合，研究了各个模型的精度和AIC值，研究为不同资料、不同地形高程测量数据的拟合提供了借鉴。