空调风系统管网风量平衡仿真调试(一)：局部构件相邻连接影响修正*

上海市建筑科学研究院有限公司 王秋涧

同济大学 潘毅群△ 黄治钟

0 引言

作为建筑调适的基础工作之一，暖通系统的测试、调节与平衡(testing,adjusting and balancing，TAB)的目的是在静态的设计工况下使系统达到水力平衡，各末端都能尽可能地达到各自的设计流量。以风系统TAB为例，由于目前国内尚没有专门详细的TAB标准，且传统风系统TAB方法(如比例调节法和逐步调节法)流程烦琐，因此在实际项目中风系统TAB工作通常不受重视，完成质量难以尽如人意。

传统方法在实际操作时需要进行大量的风量测量，费时费力。一些学者提出通过建模的方法在仿真模型中得到平衡状态时的阀门开度，并以此来指导实际调平[1-3]。总结目前各类基于常见空调系统动态仿真软件的研究工作[4-6]可以发现，绝大多数涉及风系统阻力特性仿真的研究都是将管道构件(直管、三通、弯管等)阻力系数简化为定值处理，或者直接将其忽略。当需要将仿真结果应用于实际系统时，通常需要额外的实测工作对模型的阻力参数进行校验，才能得到较为准确的压力流量结果。这是校验性的后验模拟的思路。当面对一个新的系统时，在不借助额外实测的前提下，模拟结果无法直接指导实际调试。

在构建风系统阻力构件模型时，最核心的基础数据便是阻力系数数据。其中直管段的沿程阻力相对简单，可以直接使用前人积累下来的诸多经验公式。局部阻力方面，国内外的诸多资料也有丰富的局部阻力数据表[7-12]。然而，这些局部阻力系数库的数据均针对孤立的局部构件。根据已有的构件相邻连接对局部阻力系数影响的研究结果，相邻构件的耦合总局部阻力系数与其孤立(或间距较远)时的加和值之间的偏差，最大可达到37.4%，说明相邻构件对局部阻力系数数值存在显著影响。Wang等人针对直接使用三通和风阀的孤立局部阻力系数模型所带来的误差进行不确定性分析，探究了模型误差对仿真调平结果的影响[13]。结果发现，当三通和风阀的局部阻力系数误差为±40%时，仿真调平所得到的风阀开度和风机压头的数值分布较广，模拟结果的不确定性较大。为降低仿真调平结果的不确定性，需进一步控制局部阻力系数模型的误差。

因此，本文从风系统局部构件阻力模型出发，采用CFD数值模拟的方法，针对三通、弯头、阀门3种常见局部构件的5种相邻连接关系，量化2个构件串联时对局部阻力系数的影响，并建立相应的相邻连接影响修正公式，从而为空调风系统管网风量平衡仿真调试提供支撑。

1 相邻连接影响修正方法

为量化2个构件串联对局部阻力系数的影响，本文提出将串联构件耦合总局部阻力系数的变化统一归并到下游构件局部阻力系数变化上的修正方法。在具体计算过程中，首先确定2个构件串联时的耦合总局部阻力，并计算上游构件在相同流动工况下的孤立局部阻力值(即上游构件孤立存在时的局部阻力数值)；然后用耦合总局部阻力减去上游构件孤立局部阻力所得到的剩余阻力值作为考虑相邻连接影响时的下游构件的假想局部阻力，并计算假想局部阻力系数；最后将下游构件的假想局部阻力系数与其在相同工况下的孤立局部阻力系数进行对比，计算修正系数并拟合修正公式。通过这种方法得到的修正公式可以内嵌到下游构件的局部阻力模型中，应用时较为简便。

2 算例设计与CFD数值模拟

2.1 串联构件算例设计

由于风系统中的局部构件种类繁多，连接方式也多种多样，在本文的研究过程中一次性地把所有实际工程中可能出现的构件类型和连接方式都涵盖是不现实的。出于研究可行性及成果应用性上的考虑，本课题选择了风系统中最为常见的3种局部构件：三通、阀门和弯管，并重点探究了三通接三通、三通接阀门、阀门接三通、阀门接弯管、弯管接三通5种常见的连接关系下，各个下游构件的局部阻力系数的变化规律。受实验条件限制，本文所讨论的构件为圆截面构件。对于本课题尚未直接涵盖的矩形截面构件或其他类型构件的相邻连接情况，可以针对性地增减影响因子并采用相同的研究方法得到对应的局部阻力系数模型。

本文研究的圆截面T型三通、单叶蝶阀及弯管的几何结构和细节尺寸均参照ASHRAE手册Fundamental第21章的附录[8]，见图1。

注：Q、D、A分别为构件各截面的流量、直径和面积；下标c、s、b分别代表三通的上截面、下游直通管截面和下游垂直管截面，下标o代表管道截面；r为弯管中心线曲率半径。图1 构件几何结构示意图[8]

以三通接三通的连接关系为例，其影响因子中的独立变量包括上游三通的入口雷诺数、上下游三通的下游直通管和垂直管与各自上游管之间的面积比、上下游三通的直通管(或垂直管)流量比及中间管长度，共7个变量。几何尺寸方面，本文共设计了9种三通接三通的几何尺寸组合，具体尺寸见表1。2个三通的中间连接管长度则在0.5～10.0 m范围内，等距取5水平。然后与9种三通接三通的尺寸进行全排列组合。最终三通接三通的几何模型共有45种。

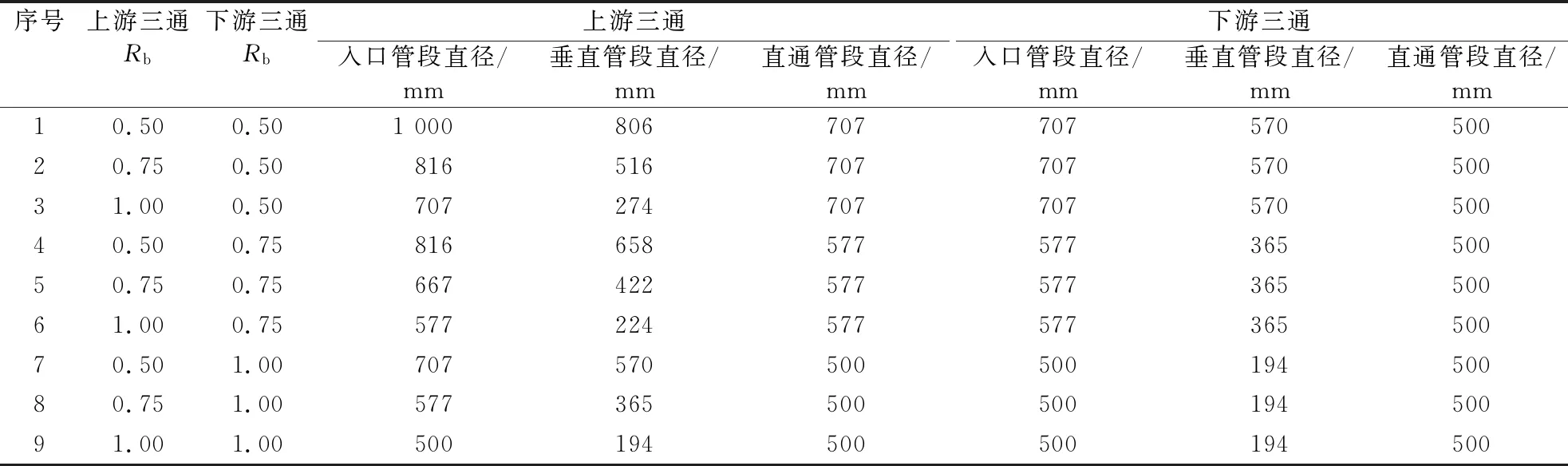
表1 9种三通接三通几何尺寸组合

对于每一个几何尺寸组合而言，涉及流动工况的参数包括：入口流速、上游三通直通管流量比及下游三通直通管流量比。本文采用均匀设计的实验设计方法[14]设计算例，流动工况参数组合如表2所示。之后流动参数组合与几何尺寸组合之间采用全排列。因此，三通接三通的总算例数为270个。

表2 三通接三通流动参数组合

其余4种连接关系的算例设计过程与三通接三通算例大致相同。表3列出了其余4种连接关系在设计算例时的影响因子及算例数。

表3 其余连接关系算例设计影响因子及算例数

2.2 孤立构件算例设计

孤立构件的算例设计过程与串联构件算例大体相同，不同的只是算例的自变量仅需要考虑构件自身的影响因子。同样为避免重复建模，孤立构件算例的几何模型均沿用串联算例中的已有模型。流动参数组合方面，保证对于串联构件算例中上游构件流动工况的全覆盖。这样在计算下游构件的假想局部阻力时，可以直接剔除上游构件在相同工况下的孤立局部阻力。因此，孤立三通共有算例54个，风阀算例108个，弯管算例18个。

2.3 局部阻力CFD数值仿真

随着计算流体力学的发展及计算效率的不断提高，CFD数值仿真方法自20世纪末以来逐渐被引入到风管构件局部阻力系数的研究中[15-20]。根据前人的风管局部阻力系数CFD仿真研究的一般结论，采用CFD模拟计算局部阻力系数时，对计算结果影响较大的因素主要包括：湍流模型、网格布置、壁面粗糙度设置等。

本文采用ICEM软件建立各个算例的几何模型并进行网格划分。图2显示了各个算例的几何模型。其中上游截面距三通入口截面1.5D1，且截面前留有长度为10D1的直管段；下游截面距三通出口截面12D1，且截面后留有长度为4D1的直管段(其中D1为水力直径)[21]。另一方面，在划分网格时，首先以算例设计流量范围内的平均流量作为验证工况进行网格独立性检验，最终选择结果稳定且网格数较少的网格设置。所有的直管段和弯管部分采用结构化网格，全局网格最大尺寸为15 mm；网格方面设置10层边界层网格，第一层网格厚度为2 mm[19]。三通部分采用边界层网格加四面体非结构化网格，边界层网格与直管段一致，四面体网格最大尺寸也设为15 mm；阀门部分采用四面体非结构化网格，最大尺寸为15 mm，阀片的面网格尺寸为2 mm。各构件截面网格分布见图3。

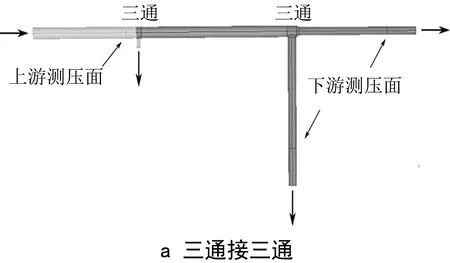
图2 CFD几何模型示意图

图3 截面网格分布

几何模型及网格划分完成后，采用ANSYS Fluent(17.2版本)软件对每个算例进行数值模拟。湍流模型采用准确度较好，且对边界层网格要求较不苛刻的标准K-ε两方程模型[19]。同时搭配Scalable壁面函数，使得在不同流速工况下采用固定边界层网格设置具有更好的稳健性。边界条件部分，入口截面设定速度入口，流速设为各个算例的对应值；入口湍流条件选择水力直径和湍流强度模式，湍流强度IT按式(1)设置；出口截面设为outflow出口，出口流量比例按算例对应值设置；壁面粗糙度设置为0.74 mm[8]，粗糙系数保持默认值0.5。压力与流速耦合算法选择SIMPLE算法。差分格式采用软件默认格式。残差部分，连续性残差设为10-3，其余变量残差均设为10-5。其他未提及设置均采用17.2版本Fluent的默认设置。待Fluent数值计算完成后，将上下游测压面的全压、动压值输出，计算从上游三通入口段到下游三通的下游直通管和垂直管之间的全压差，留待备用。

IT=0.16Re-0.125

(1)

3 局部阻力构件相邻连接影响修正

3.1 孤立构件局部阻力系数模型

根据第2章所述的相邻连接影响修正方法，在进行修正前需要建立构件孤立存在时的局部阻力系数模型，从而计算串联构件中下游构件在相同工况下的孤立局部阻力系数。根据ASHRAE局部阻力系数测量标准[21]的规定，三通的直通管局部阻力系数ξb和垂直管局部阻力系数ξv的计算公式见式(2)、(3)，阀门和弯管的局部阻力系数ξ计算公式见式(4)。其中风阀和弯管沿程阻力的计算包括风阀和弯管本身的长度。

(2)

(3)

(4)

式(2)～(4)中p为截面动压；ps为截面静压；Δpf为上、下游测压面的沿程阻力；下标u、b和v分别表示上游、直通管和垂直管；pt,u、pt,d分别为上、下游测压面的全压；ΔpF为直管段沿程阻力。

在第2.2节的孤立构件算例数据基础上，针对三通和风阀构件，采用支持向量机回归(SVR)方法，并辅以粒子群优化算法(PSO)，对支持向量机回归的惩罚系数C及径向基核函数的gamma参数进行寻优，以提高拟合效果。寻优过程中采用10折交叉检验策略，以使所得到的SVR模型具有更好的外延特性。另外，由于局部阻力系数各个数据点之间量级差异较大，所以采用拟合结果的平均绝对百分比误差作为优化的目标函数。

拟合时，由于在舒适性空调所涉及的空气温度范围内，空气的物性参数变化不大，本文采用入口流速管径比(入口流速与入口管径之比)作为自变量，近似代替入口雷诺数Re。在拟合三通局部阻力系数时，自变量还包括上下游面积比和流量比。在拟合孤立风阀的局部阻力系数模型时，自变量为阀门开度和入口流速管径比。

为了验证孤立三通局部阻力系数PSO-SVR模型的准确性，另外选择一个标准尺寸的圆截面三通，采用同样的CFD设置计算该三通在不同支路流量比下的局部阻力系数，并将其与PSO-SVR模型的对应输出结果进行对比。该三通的上游管、直通管、垂直管的直径分别为250、200、200 mm。入口流量为600 m3/h。其几何尺寸和流量分配的组合未出现在训练集中。对比结果如图4所示。可以看到，PSO-SVR模型输出的局部阻力系数与CFD直接计算结果整体趋势保持一致，相同工况下的局部阻力系数差值较小。孤立风阀模型的验证方面，本文选择与ASHRAE手册中的直径350 mm的圆截面蝶阀局部阻力数据[8]进行对比。如图5所示，PSO-SVR模型的输出结果与ASHRAE手册数据的趋势线几乎重叠，从而验证了孤立三通和风阀的拟合模型准确度。

图5 孤立风阀局部阻力系数PSO-SVR模型的验证

对于弯管模型而言，以入口流速管径比为自变量对局部阻力系数进行线性拟合，如图6所示。可以看出，弯管的局部阻力系数与自变量入口流速管径比呈现显著的线性关系，拟合效果较好。

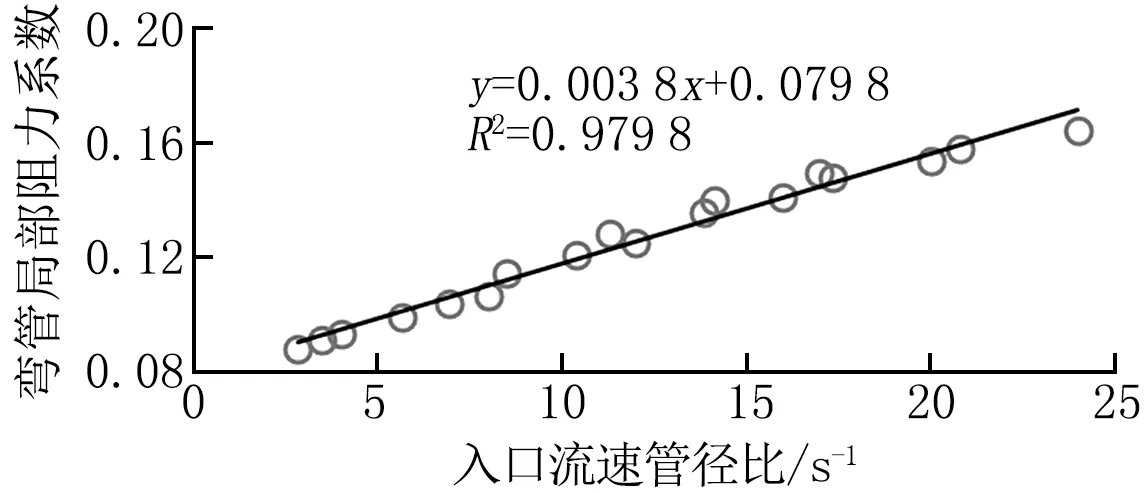
图6 孤立弯管局部阻力系数线性模型拟合结果

3.2 相邻连接影响修正模型

在对构件相邻连接影响进行修正时，首先需要对考虑相邻连接影响下的局部阻力系数的修正系数进行定义，然后根据各算例结果计算修正系数的具体数值，最后根据各算例中的影响因子对修正系数进行拟合，并得到最终的修正公式。表4罗列了所有连接关系的下游构件局部阻力系数修正系数定义式、修正系数拟合公式、可决系数R2、F检验统计量F值及平均绝对百分比误差EMAP。其中，可决系数R平方值越接近于1，表明拟合效果越好；F值越大，表明拟合模型的整体显著性越高。

表4 各连接关系的下游构件局部阻力系数修正系数、拟合公式及拟合效果

对于大多数的连接关系，修正系数的定义式为考虑相邻连接影响的下游构件假想局部阻力系数和孤立时的局部阻力系数之间的比值。而当下游构件为三通直通管时，修正系数不再是简单的二者之比，而是把考虑相邻连接影响的垂直管局部阻力系数作为基数，同时添加到修正公式的分子和分母当中。这么做的原因在于：直通管局部阻力系数有许多数值分布在0附近的点。如果按照与垂直管修正系数相同的定义方法，则会出现修正系数值非常大的情况，有的甚至超过105。采用上述处理可以使得直通管局部阻力系数的修正系数值基本分布在1附近的合理区间内。

在拟合修正系数时，本文主要采用stepwise逐步回归法进行齐次多项式拟合，多项式模型的最高阶次根据在满足拟合精度要求且没有过拟合的前提下选择更小阶次的原则来确定。以上游串联三通时的三通垂直管局部阻力系数修正模型为例，其多项式修正模型的各项系数如表5所示，修正系数由各变量值与对应系数值的乘积加和得到。其余多项式修正模型的形式与之类似，出于篇幅的考虑，本文未列出其余多项式模型系数表。对于一些特殊情况，如上游构件为阀门的连接关系，其修正系数无法直接通过多项式拟合获得较好的拟合效果。通过观察修正系数关于其个别影响因子的分布情况，并采用常见曲线方程进行反复拟合试验，笔者发现针对这些连接关系的修正系数采用分两项拟合的方法效果较好。一项为个别影响因子的曲线拟合项(幂函数/指数函数)，另一项为剩余影响因子的多项式拟合项。不同连接关系的多项式修正公式的阶次不尽相同，如三通直通管接三通垂直管的最高阶次为二次，而三通直通管接三通直通管则为三次。这是由各修正系数的不同的数值分布情况所决定的。

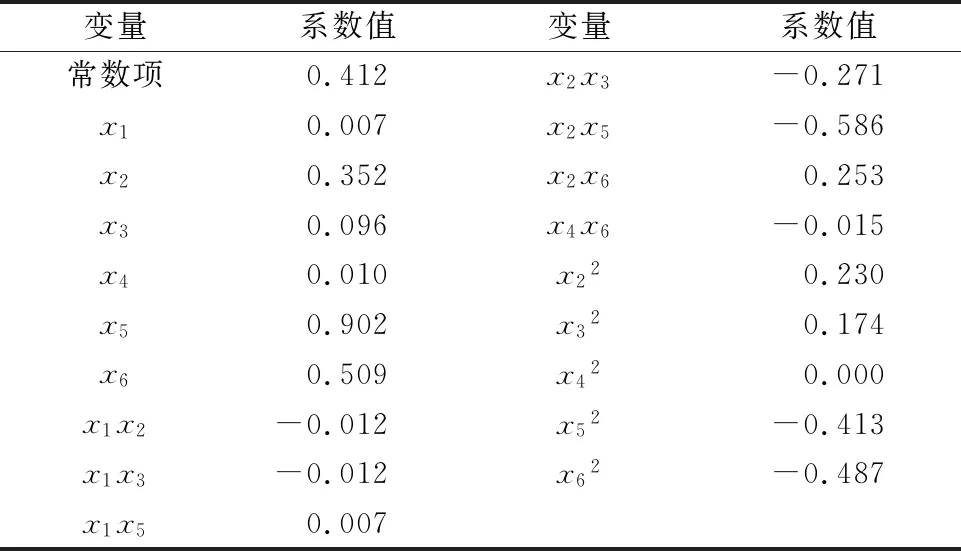
表5 上游串联三通时的三通垂直管局部阻力系数多项式修正公式系数

另外，在本文涉及的连接关系中，并非所有的连接关系都需要对相邻连接影响进行修正。在三通直通管接阀门的连接关系中，笔者发现上游串联三通直通管时的阀门局部阻力系数与阀门孤立存在时的数值差异较小，下游阀门的假想局部阻力数值与其孤立值之间的误差值小于10%。其误差满足文献[13]中确定的仿真调平对阀门局部阻力系数的误差控制要求。因此，本文未对上游串联三通直通管的阀门局部阻力系数进行修正，而是直接沿用孤立存在时的阀门模型，对应修正系数为1。

本文采用平均绝对百分比误差EMAP来评价修正模型在各串联构件算例数据集上的准确性，其计算式如下：

(5)

式中N为串联构件数量；ξ为局部阻力系数；下标p为模型计算值，r为受上下游相互影响的真值。

需要说明的是，对于某些数值在0附近的样本点，若直接计算该点的相对误差绝对值，原本非常微小的误差在除以在0附近的局部阻力系数真值后，会导致相对误差绝对值异常巨大。这样的点并不能客观反映模型的准确程度。为了排除这些真值在0附近点的干扰，笔者以±0.05为限，当局部阻力系数的修正值和真值的数值均在[-0.05，0.05]之间时，则忽略这一点的误差，使该点不参与平均绝对百分比误差的计算。

从表4中的平均绝对百分比误差结果可以看出，各个连接关系由于其各自修正系数的分布情况各有不同，因此采用大致相同的拟合方法所带来的模型误差存在一定的差异。各种连接关系修正公式的平均误差为13.00%，其中修正效果最好的是三通直通管接三通垂直管，平均绝对百分比误差仅为2.48%，而最差的为阀门接三通直通管，平均绝对百分比误差为22.18%。总的来说，当下游构件是三通直通管或上游构件是阀门时，修正后的误差相对要大一些。原因有两点：一是三通直通管的局部阻力系数数值本身较小，在受到相邻连接影响时产生的变化较大，且与自变量之间的非线性关系程度较高；二是阀门的局部阻力系数相较于三通和弯管而言数值要大得多，当把上游阀门所受到的来自下游构件的影响也归结到下游构件的局部阻力系数变化上时，下游局部阻力系数产生的变化较大，同样与其自变量之间的非线性关系程度较高。在拟合时受到过拟合风险的限制，不能将多项式模型的阶次无限制地提高，否则即使拟合误差较小，拟合模型的内插和外延准确性也不会很好。表4中的误差结果是笔者经多次尝试，在拟合误差和过拟合风险之间权衡之后得到的结果。

图7～14分别对各个连接关系中考虑上游影响的下游构件局部阻力系数的修正值和未修正的孤立值进行了对比。以图7为例，可以看出，修正前，上游串联三通时的三通垂直管局部阻力系数与其孤立存在时的局部阻力系数之间的误差非常大。例如，当三通垂直管局部阻力系数在上游串联三通时的数值为3.0左右时，孤立存在时的值为10.5左右，后者约为前者的3.5倍。如此量级的局部阻力系数误差势必会对管路流量分配的计算结果产生较大影响。修正之后，所有数据点基本均匀地分布在理想的45°线附近。类似的修正效果也可以在其余连接关系中看到。修正后数值相比于修正前的孤立值，均大幅接近考虑相邻连接影响的假想局部阻力系数值，表明修正模型可以较好地描述相邻连接对于局部阻力系数的影响。

图7 上游串联三通直通管时的三通垂直管局部阻力系数修正结果

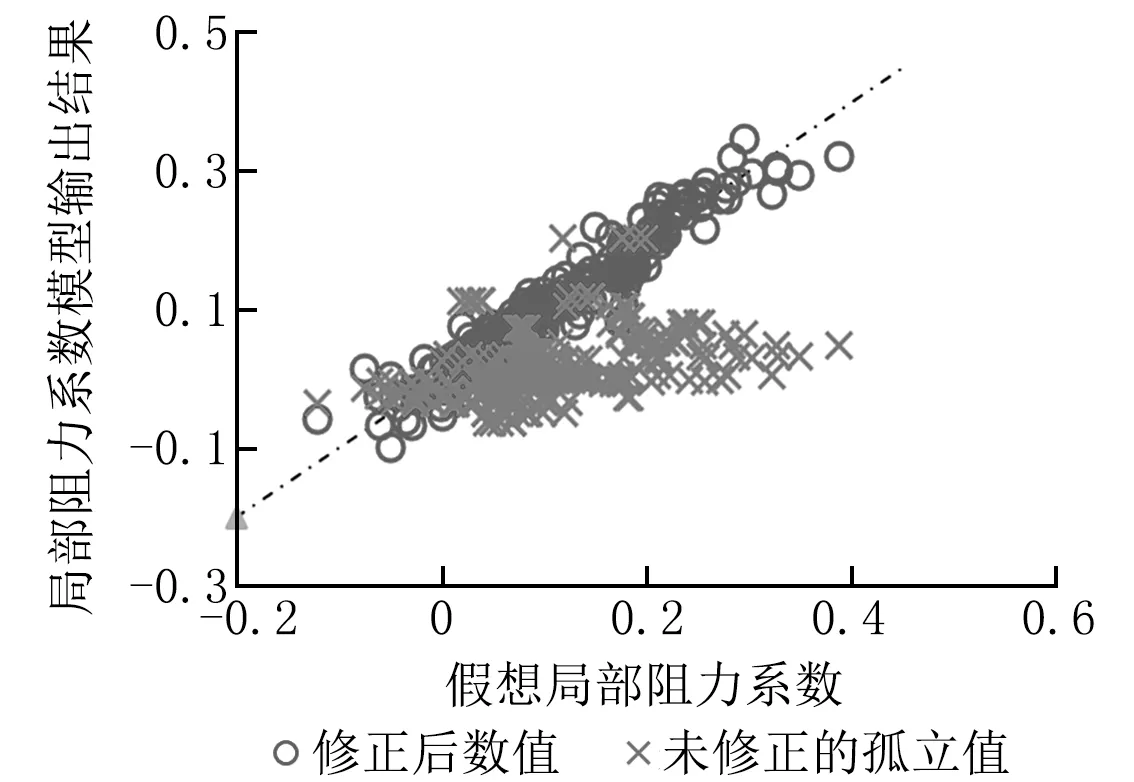
图8 上游串联三通直通管时的三通直通管局部阻力系数修正结果

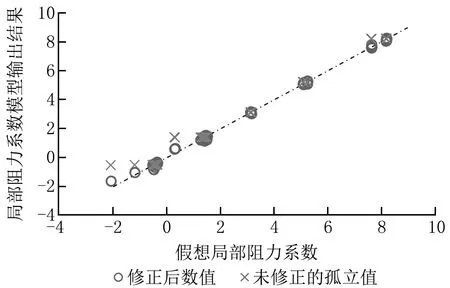
图9 上游串联三通垂直管时的阀门局部阻力系数修正结果

图10 上游串联阀门时的三通垂直管局部阻力系数修正结果

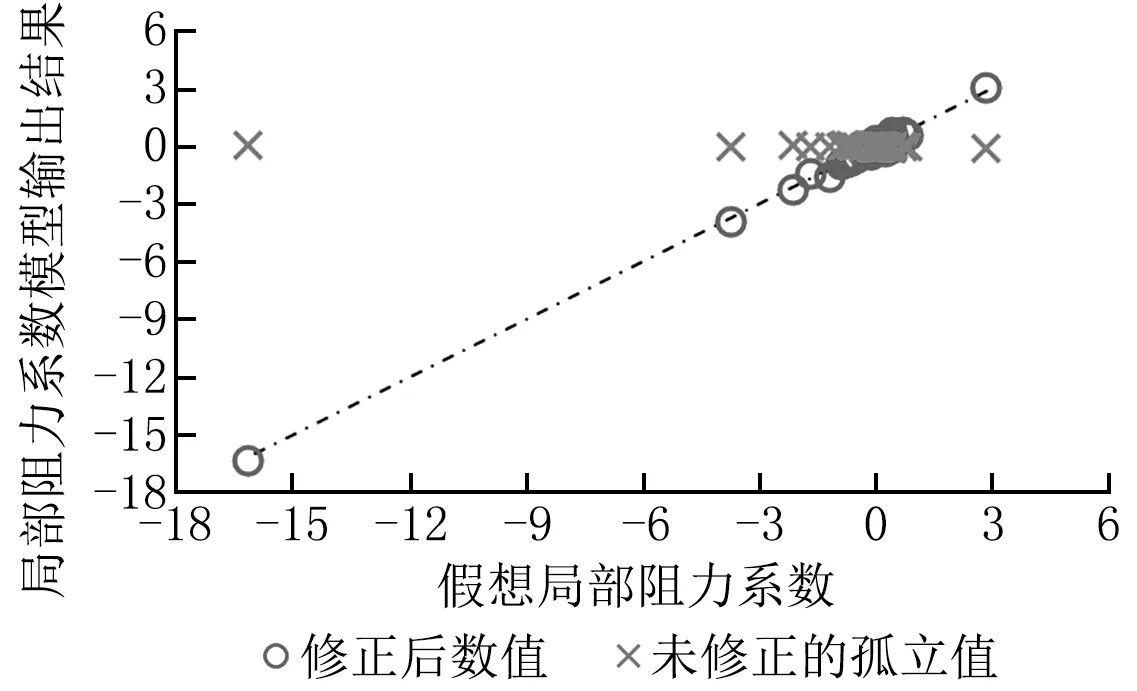
图11 上游串联阀门时的三通直通管局部阻力系数修正结果

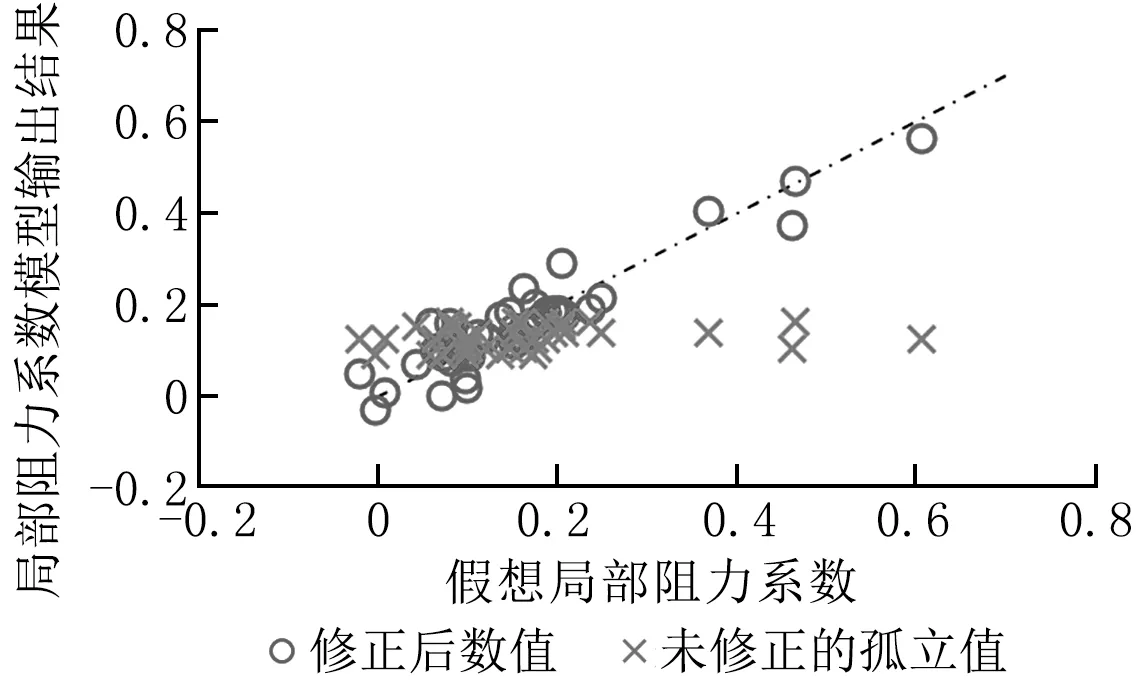
图12 上游串联阀门时的弯管局部阻力系数修正结果

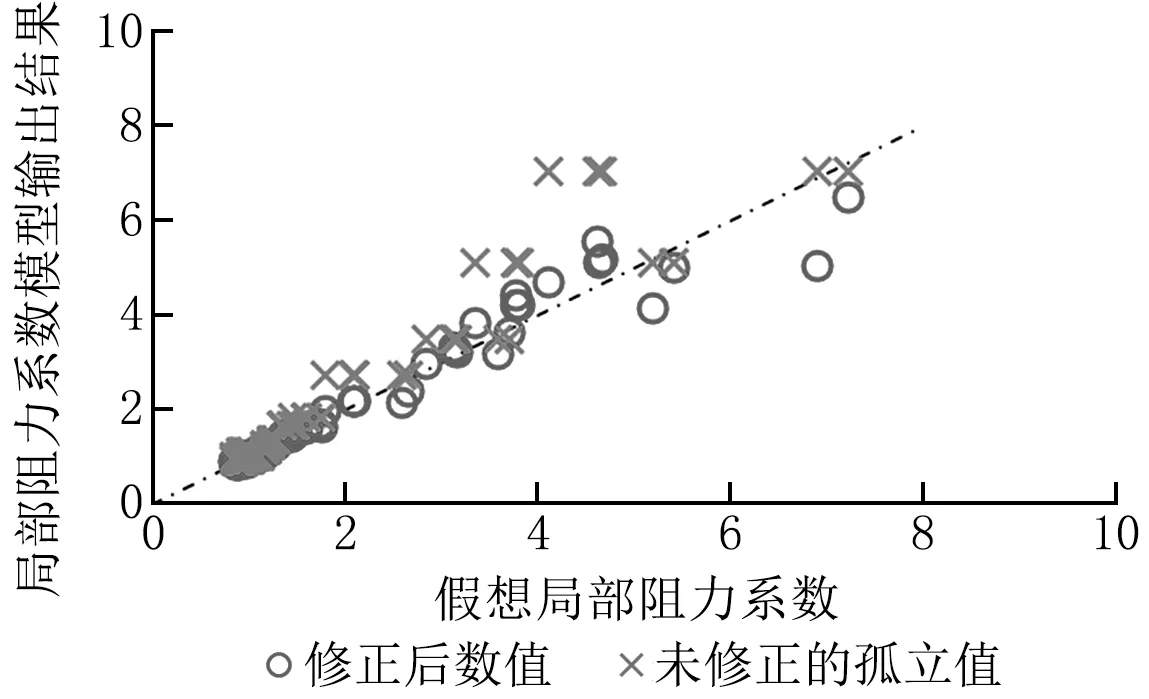
图13 上游串联弯管时的三通垂直管局部阻力系数修正结果

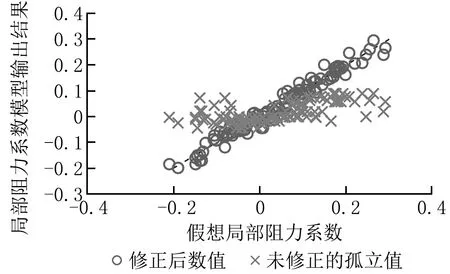
图14 上游串联弯管时的三通直通管局部阻力系数修正结果

4 结语

为提高风系统管网构件阻力模型的准确性，针对三通、弯管和阀门这3种最常见的风管构件的5种连接方式建立了相应的局部阻力系数修正模型，为风系统管网仿真调平提供模型支撑。从最终的修正结果来看，本文提出的将2个构件近距离串联时的相互影响统一归并到下游构件局部阻力系数变化上并对其进行修正的方法，可以准确地反映构件相邻连接对局部阻力系数的影响。同时，本文采用的算例设计、CFD数值模拟、修正模型拟合的一整套研究方法可被推广到其他类型构件的局部阻力系数模型和修正模型的研究中。

目前，虽然本文所涵盖的构件类型和连接方式的范围仍十分有限，还不足以支持对于任意实际空调风管系统的阻力仿真，但针对其他常用构件类型和连接方式，未来可以套用本文的一整套研究方法建立更为广泛的局部阻力系数数据库和修正模型库。虽然搭建一套完整的数据库工作量较大，但其本质上是一种一劳永逸型的科研投入。当数据库涵盖的构件类型和连接方式足够全面时，应用这些模型进行空调风系统仿真调平的过程将会极其简便。甚至可以采用与BIM模型对接的方式完成自动化建模，调用局部阻力系数模型进行调平计算，并最终实现采用仿真调试指导实际现场调试的构想。