基于不确定性量化分析的超低能耗建筑空调系统运行能耗研究*
2021-06-02上海市建筑科学研究院有限公司赵德印
上海市建筑科学研究院有限公司 赵德印 徐 强
0 引言
受内部和外部各种复杂因素的影响,在工程实践中存在着大量的随机不确定性和认知不确定性,因此如何通过一定的技术手段来提高工程系统的稳健性显得尤为重要。以美国Sandia国家实验室为代表的众多研究机构提出使用不确定性量化来有针对性地解决稳健性、提高系统可靠性,获得了一系列研究成果[1]。迄今为止,不确定性量化的研究方法已经广泛应用于结构工程、机械工程、核工程、武器设计、建筑能耗等工程和研究领域[2-6]。
建筑能耗不确定性量化研究涵盖内容较多,一般包括空调、通风、照明、热水、动力等方面。如Lamberti等人对美国斯坦福的Y2E2建筑进行了夜间通风节能的不确定性量化研究。自然通风由于风压不稳定而存在较大的不确定性,计算节能潜力与实际效果相差较大,因此在设计中偏重考虑热压通风的作用。作者首先基于经验给定不确定性变量,包括窗户流量系数、表面传热系数、墙体内表面温度及内部得热的概率分布,然后利用CFD模拟以修正概率分布,最后将不确定性变量代入建筑整体模型进行夜间通风潜力分析[7]。Pang等人利用EnergyPlus对5个不同城市气候区的旅馆热水用水量进行了不确定性和敏感性分析,输入先验变量161个,抽样计算15 000次,经数据分析指出,最大热水能力和热效率是影响洗衣房燃气消耗量的关键因素,厨房中关键因素则为进出水温度,对于热水消耗量而言,关键因素是用水设备的最大出流量;此外,人员行为对热水消耗量和燃气消耗量均有较大影响[8]。Yan等人对空调新风机组进行了测试,结果表明利用风阀调节新风量和新风比时存在较大不确定度;基于实测数据对其进行不确定性量化处理并代入EnergyPlus进行分析,能耗模拟结果表明,与基准模型相比,考虑新风不确定性后的制冷能耗相差17%,制热能耗相差43%[9]。Domínguez-Muoz等人阐述了利用输入变量不确定性确定建筑峰值负荷的方法,与传统的单次计算、取安全系数等方法相比,新方法根据模拟结果概率分布曲线确定建筑峰值负荷,能在有效降低峰值负荷的同时规避风险[10]。Tian等人针对不确定性研究方法在建筑能源评估中的应用进行了文献综述,分别从不确定性来源、正向和逆向分析方法、应用软件等方面介绍了国内外的研究进展,并乐观预测不确定性研究方法将成为建筑能源评估分析的主流方法[11]。
由以上文献资料分析可知,不确定性量化研究方法的优势在于尽最大可能考虑了不同输入变量的不确定性,通过一定的数学抽样方法提取不同变量组合进行多组能耗模拟计算,最终生成目标对象的累积概率分布曲线,帮助设计者在考虑风险的同时进行决策。
当前不确定性量化研究方法在建筑空调系统中主要用于额定负荷、零部件性能、设备容量确定等研究,研究结果更多的是帮助设计师进行风险决策。本文引入该方法,在尽可能考虑实际运行条件的前提下,对超低能耗办公建筑进行运行能耗评估,探索该类型建筑的运行能耗下限值。
1 研究方法
本文利用该方法对一栋办公建筑进行全年空调能耗分析,研究思路为:首先分析相关输入参数并确定先验分布,然后建立能耗模型并进行抽样计算,最后建立能耗的累积概率分布曲线以确定空调能耗并进行输入变量敏感性分析,如图1所示。研究主要采用DesignBuilder软件[12],该软件以EnergyPlus为计算核心,使用OpenGL固体建模器,具有优秀的图形界面操作能力,界面友好,易于操作,能通过拉伸、剪切等三维建模命令对复杂建筑进行建模,建模效率较高。不确定性量化分析采用软件中的Optimisation+UA/SA模块,样本采样方法选用random,经采样生成变量的样本组合后代入能耗模型中进行计算并作统计分析。
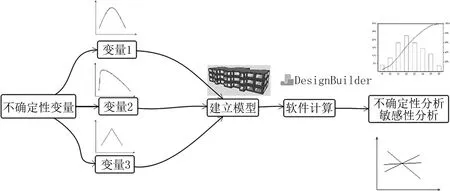
图1 分析流程图
在不确定性分析完成并获取最终数据样本后,一般均进行敏感性分析,用于辨识输入变量的重要程度。敏感性分析起初是经济学中用于投资项目风险评价的一种动态不确定性分析法,应用该方法能找出对项目经济效益影响最大的敏感性因素并量化,从而为项目风险决策提供科学依据[13]。本文采用多元线性回归法建立输入变量和能耗的关联式,进行各输入变量的敏感性分析。
2 研究对象
目标建筑为上海市一栋办公建筑,总建筑面积2.3万m2,其中地上建筑空调面积约8 640 m2,主楼6层,副楼3层,建筑总高度24 m,使用DesignBuilder软件建模,如图2所示。依据公共建筑节能设计要求并结合业主提出的建筑功能需求,确定建筑围护结构参数、空调设计温度、相关热扰参数等,如表1所示。该建筑空调形式为多联机+新风系统,工作时间为工作日08:00—18:00。

图2 目标办公建筑模型
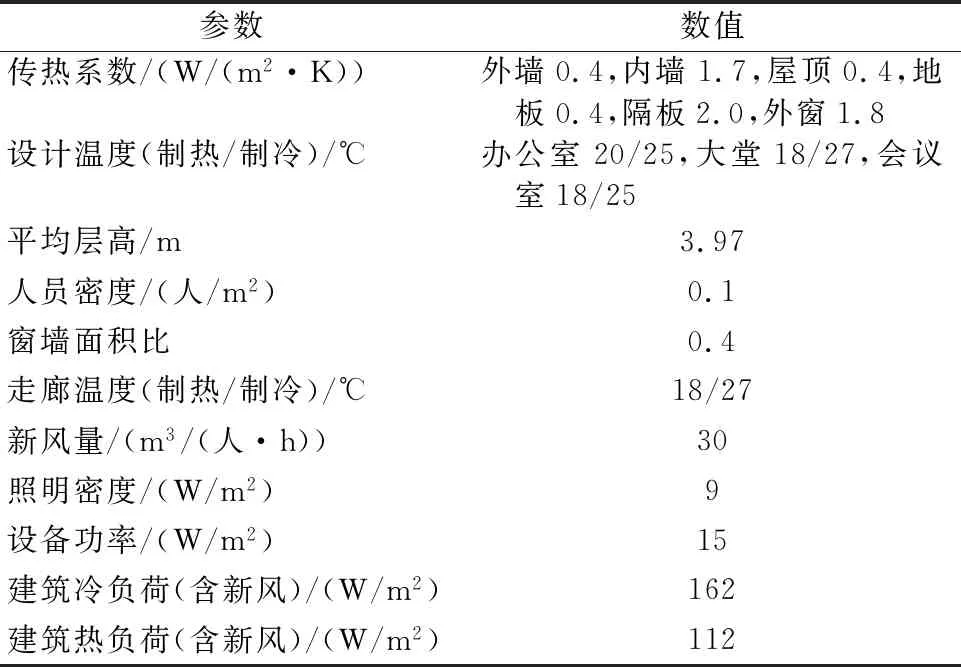
表1 建筑参数设置
3 参数不确定性辨析
严格来说,能耗计算所需要的所有输入变量均存在不确定性。以下分别对各类变量的不确定性类型和存在原因加以详细说明。
1) 建筑本体的固有属性变量。主要是围护结构的热工参数,包括材料的导热系数、密度、比热容等,该类参数由于实际建筑使用材料和标准测试材料之间存在差异,因此在模拟计算时输入的变量存在系统偏差和测量误差。
2) 建筑使用相关的可变变量。主要是建筑运行中的实际运行时间表、人员密度、人员行为、空调系统运行策略、房间设备、灯光开启密度等变量,其特点是用户自由控制时,该类变量变化范围较大,单一工况模拟时,固定的取值将会造成模拟结果的较大偏差,但是当采取集中控制、严格管理时,该类变量即可认为是固定取值。
3) 不受控制的变量。该类变量是系统模拟的重要输入参数,包括气象参数、建筑气密性、空调系统性能等。其中气象参数只能被动测量,测量时存在测量误差,无法实施人工干预,模拟计算时多使用典型气象年数据,与历年实测数据之间存在差异,属于系统偏差。建筑气密性和空调系统性能类似,在建筑建成投入使用后其基础性能即确定,而基础性能受制造、安装等人为因素影响,与此同时,室内外温度、温差又直接影响两者的实时性能,因此模拟时采用单一工况固定数值会导致一定偏差。
4) 建模误差。主要是指建筑模型尺寸与设计尺寸之间的偏差,一般能耗建模均根据设计图纸手动近似建模,房间使用面积、墙体厚度、空间功能布局等无法做到模型与实际建筑完全一致,该部分误差无法消除,但是在计算机硬件、计算时间等满足要求的条件下,可以尽量细化建模以减小误差。
5) 制造偏差。主要是指建筑建造过程中,构件浇筑、加工制造过程中的尺寸偏差,比如墙体厚度等,这些偏差会导致墙体的热阻出现偏差,从而影响空调能耗的计算准确度。
事实上在模拟分析建筑能耗时,需要在计算成本与计算精度之间寻求平衡,即尽可能寻找影响建筑能耗的关键变量并建立其变量概率分布密度函数。
Li等人针对香港地区零能耗/低能耗建筑进行了不确定性计算研究,主要考虑的不确定性因素包括气象参数、渗透系数、内部负荷等[14]。de Wilde等人研究了考虑气候变化条件下的建筑负荷变化,研究结果表明,建筑渗透性能、灯光和设备发热是影响制热负荷的关键因素,影响制冷负荷的主要因素主要是灯光和设备发热及高排放情景下的气候条件[15]。Belazi等人重点研究了人员上下班时间、人数变化及围护结构对寒冷地区、炎热地区、温和地区建筑能耗的影响,其中炎热地区人员行为变化对能耗影响较大,而在寒冷地区则围护结构更为重要[16]。这间接表明建筑能耗的不确定性分析需要考虑气象条件。
本文研究对象为一栋新建成投入使用的装配式超低能耗办公建筑,墙体采用预制件装配而成,建造中有样品检验、现场检验等过程以保证建筑性能达到设计要求。该建筑是公司自有建筑,主要供公司内部员工办公使用,员工上下班作息时间明确。因此可以认为前述不确定性因素1)、2)、5)变化较小,认定为固定变量,不确定性因素4)没有明确的变量,无法测量,只能尽量依据图纸建模,减少模型误差。
因此在不确定性分析时,本文主要考虑具有较大不确定性的输入变量,主要包括:1) 气象数据,2) 渗透换气次数,3) 自然通风换气次数,4) HVAC性能指标制冷季节能效比(SEER)、制热季节能效比(HSPF),5) 人员密度。
以下分别对各输入变量的概率分布函数进行分析说明。
3.1 气象数据
在能耗模拟中,气象数据文件是影响模拟准确性的一个重要因素,目前各不同能耗模拟软件均自带气象数据文件。朱明亚对目前常用的各类型气象数据文件,如IWEC(international weather year for energy calculation)、CSWD(中国标准气象年)、SWERA(solar and wind energy resource assessment)、CTYW(中国典型年)作了汇总,这些气象数据文件使用不同来源、不同历史年份的天气数据,主要使用Finkelstein-Schafer(FS)统计分析方法、根据不同判断准则制作而成[17]。此外,具体到每一年的气象数据之间也存在差异。本文对CSWD、2008—2017年共计11个气象数据文件作了统计对比分析,如图3、图4所示。由图可知,基于度时(日)数法的空调冷负荷近10年来呈现大幅增加的趋势,而供暖热负荷则呈现略微下降趋势。相对于标准气象年基准数据,空调度时数CDH26最大值增加了151%,供暖度日数HDD18最小值仅降低了10%左右。进一步分析月平均温度可知,近10年中(2008—2017)7月和8月的平均温度明显高于标准气象年对应温度,如图5所示,该时间段正是空调用电高峰期,表明采用近年气象数据文件计算时其空调制冷能耗将高于标准气象年文件的计算结果。Wang等人对一栋办公建筑的研究也表明,不同年份的气象数据导致的能耗变化幅度约为-4%~6%[18]。因此在进行不确定性分析时,采用CSWD、2008—2017年共计11个气象数据文件进行计算。
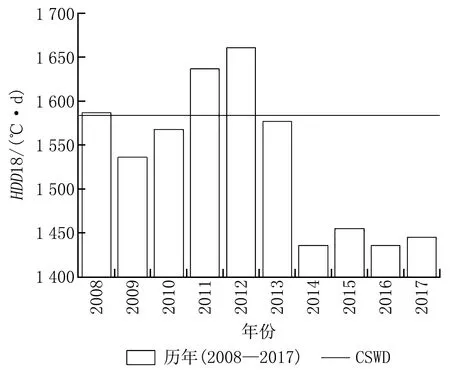
图3 供暖度日数对比

图4 空调度时数对比

图5 月平均温度对比
3.2 渗透换气次数
建筑渗透换气性能与建筑能耗密切相关,有文献研究表明,渗透换气造成的供暖能耗占居住建筑总能耗的比例为15%~45%[19]。相对而言,公共建筑的建筑本体气密性要优于居住建筑,同时个性随机调节行为等的发生频率也低于居住建筑,但是其由于渗透造成的建筑能耗也不能忽略。
一般而言,渗透换气性能优劣受建筑施工工艺、建筑用途、建成年限等因素影响,不同建筑其数值不尽相同,相应的建筑能耗变化也较大。Heo等人基于既有建筑实际测试数据,利用贝叶斯推断方法得到了建筑渗透系数后验概率分布,如图6a所示,80%以上的数据集中在0.75~1.10 h-1之间[20]。Macdonald汇总了建筑能耗不确定性研究结果,对美国、英国、瑞典、挪威等国的建筑渗透性能作了总结,如图6b所示,渗透换气次数平均值分布在0.10~0.35 h-1之间[21]。结合图6研究成果,本文研究对象的建筑渗透换气次数取值范围定为0.35~1.25 h-1,参数分布函数取为正态分布N(0.75,0.192)。
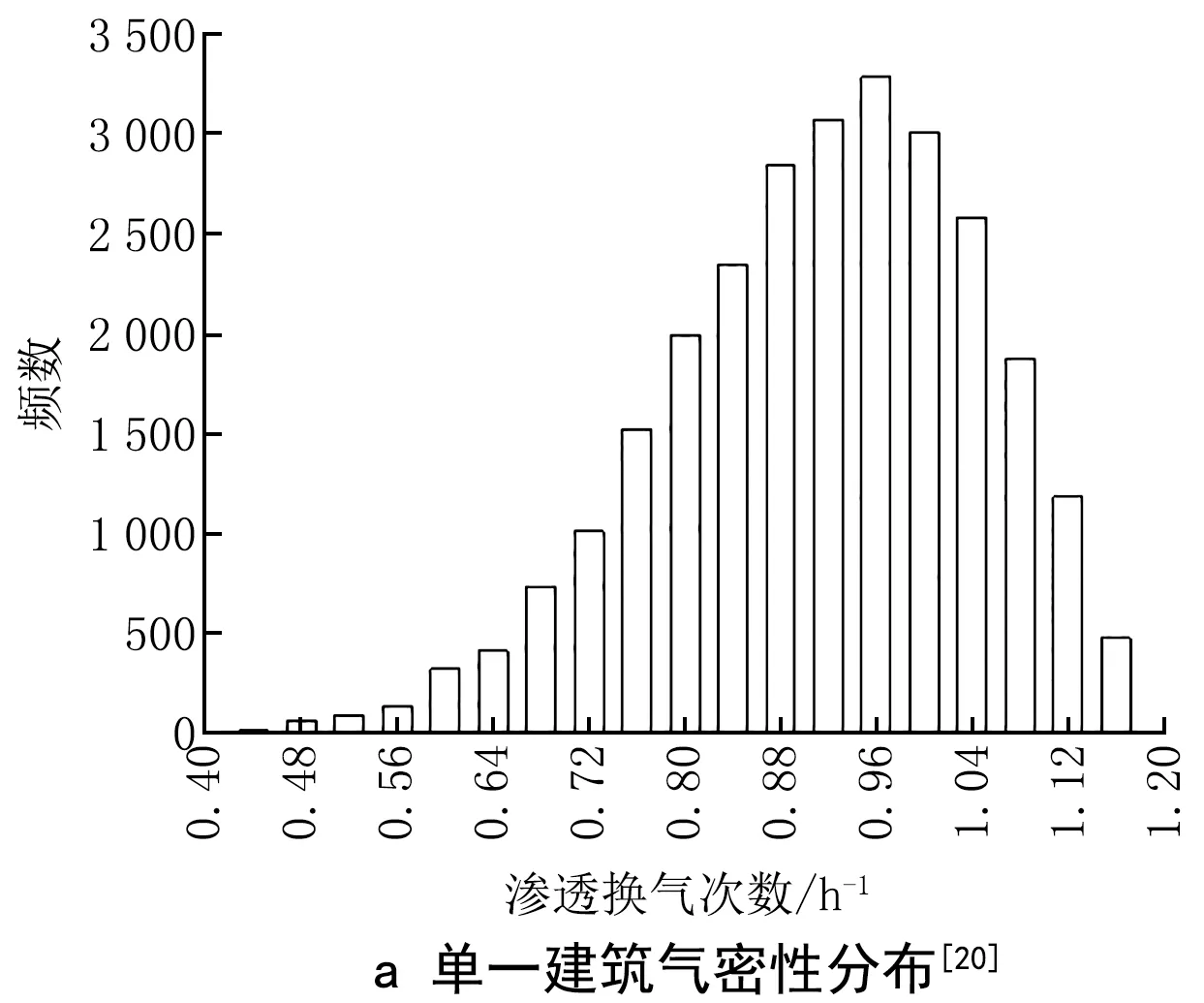
图6 建筑气密性研究成果
3.3 自然通风换气次数
单纯依靠建筑合理设计及运行实现建筑超低能耗甚至近零/零能耗等目标较为困难,合理利用可再生能源降低建筑运行能耗较为关键。本文研究的目标建筑空调系统依赖电网电力输入,没有可再生能源发电补偿,因此主要考虑利用自然通风降低空调能耗。
过渡季节应用自然通风具有较好的节能潜力,而自然通风分为热压通风和风压通风,驱动力分别为热压和风压。除室外气象条件外,自然通风的影响因素还包括:室内门窗开口面积、室内热扰等。为确定自然通风换气次数,本文采用计算法对该目标建筑自然通风换气次数进行了不同开窗面积下的对比计算,如图7所示,当外窗开口面积为10%时,换气次数明显偏大,而当外窗开口面积为5%时,其换气次数可达到4 h-1。因此在考虑自然通风换气次数的不确定性时,取其概率分布为均匀分布,间隔1 h-1,上限为4 h-1,下限为1 h-1,只在过渡季节开启运行,运行时间设置如表2所示。
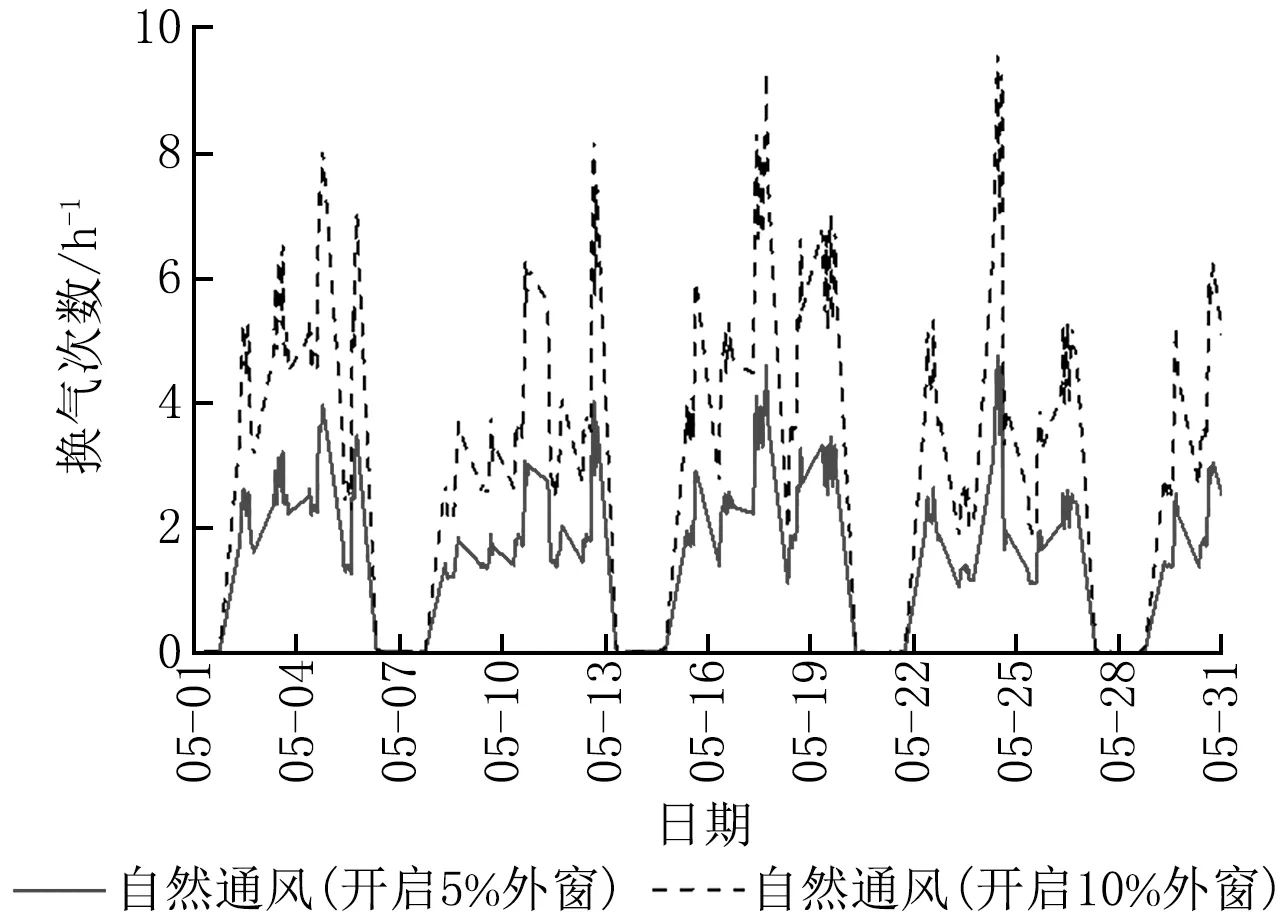
图7 自然通风换气次数
3.4 多联机SEER/HSPF
多联机全年性能系数(APF)、SEER、HSPF的主要表达式如式(1)~(5)所示,其余用于计算的公式详见多联机标准附录[22]。
(1)
(2)
(3)
(4)
(5)
式(1)~(5)中Lc为制冷季节总负荷,kW·h;Ec为制冷季节耗电量,kW·h;Lh为制热季节总负荷,kW·h;Eh为制热季节耗电量,kW·h;Rhc为热冷负荷比;Lc(tj)为室外温度tj时建筑物的制冷负荷,kW;j为制冷季节温度区间序号,j=1,2,3,…,18,19;m为室外温度tj=35 ℃时的温度区间序号;φful(tj)为室外温度tj时机组以名义能力运行时的制冷量,kW;nj为制冷季节需要制冷的各温度发生时间,h。
综上可以看出,多联机当前季节能效比计算的主要方法是根据额定性能、中间性能、最低性能、低温性能(制热)实测数据,利用相关线性方程求解各温度区间下的对应性能参数,从而求解SEER、HSPF、APF。
由式(1)~(4)进一步推导,可以得到APF与SEER、HSPF的关系式,如式(6)所示。
(6)
由式(6)可知,当Rhc已知时,即可求解得到SEER、HSPF、APF三者之间明确的关系式。
为求解SEER、HSPF,根据相关规范[23-24],取Rhc=0.7,根据实际调研机组性能数据[25],取APF=4.5,并定义如下变量:
(7)
(8)
式(7)、(8)中x、y分别为制冷性能比例因子、制热性能比例因子。
求解式(6)~(8)并代入相关数值可得:
(9)
根据式(9)绘制x、y变化趋势图,如图8所示。结合实测机组性能数据,本文研究中选取变量合理变化区间为:y∈[0.70,1.00],x∈[1.00,1.43]。由于进行不确定性分析时要求各因素之间相互独立,因此SEER、HSPF的取值范围分别为[3.6,4.5]、[3.15,3.60]。由于多联机实际安装及运行状态复杂多变,设定两者的概率分布均为正态分布,方差取默认设置,其中制冷季节能效比分布函数为SEER~N(4.05,0.52),制热季节能效比分布函数为HSPF~N(3.375,0.52)。

图8 HSPF/APF(y)随SEER/APF(x)变化趋势图
3.5 人员密度
在实际办公建筑运行中,一天之中不同时刻的人数是不同的,在模拟过程中,不同时刻的人数通常使用运行时间表来控制,如图9所示。则任意时刻的在室人数可用如下公式表达:
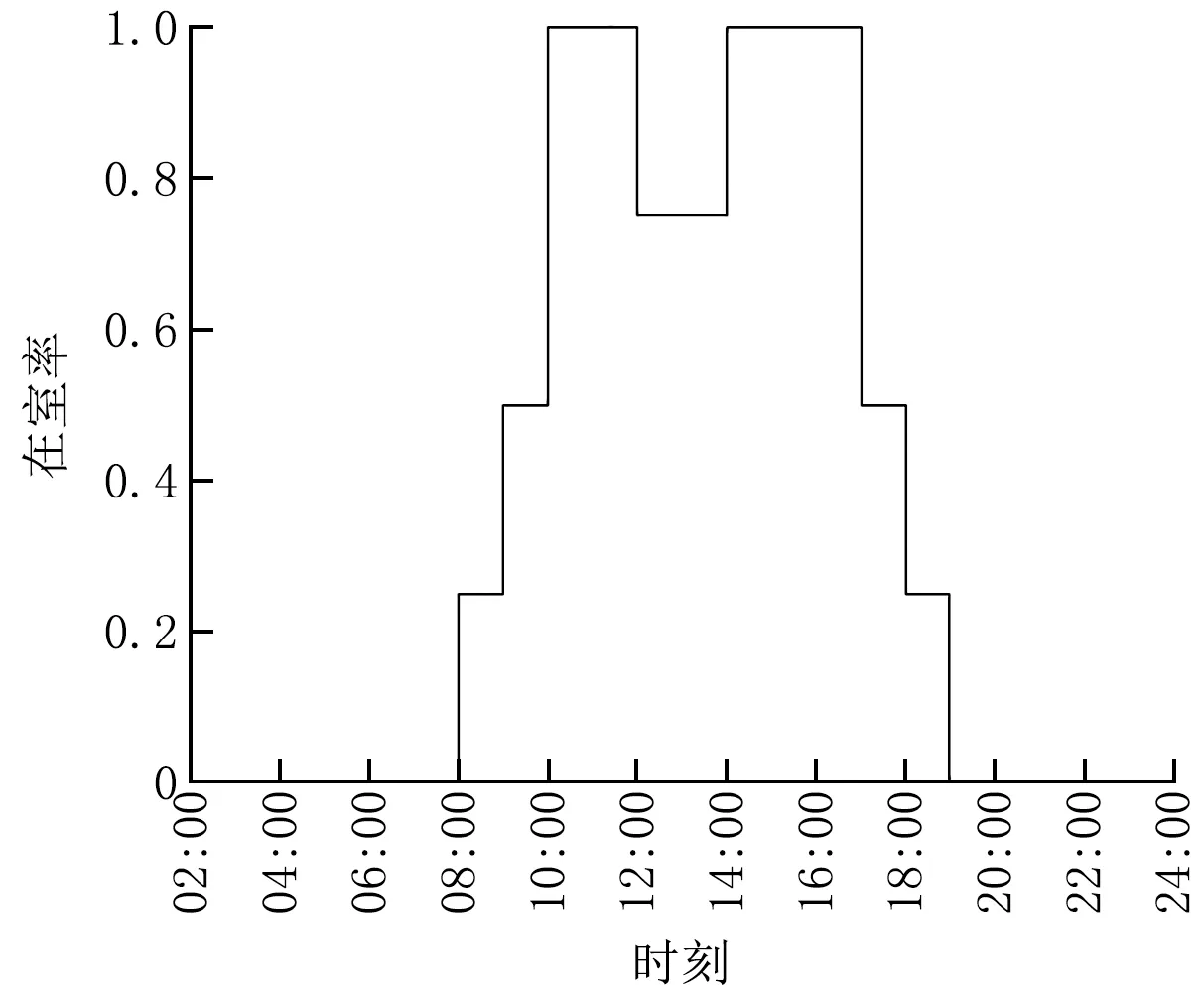
图9 人员逐时时间表[26]
Oo=DpAzSs
(10)
式中Oo为任意时刻在室人数,人;Dp为人员密度,人/m2;Az为热区面积,m2;Ss为运行时间表。
在进行建筑不确定性模拟时,人员密度一般参考规范或者设计经验取一定值,如GB 50189—2015《公共建筑节能设计标准》中推荐的人员密度为0.1人/m2[26],GB 50189—2005《公共建筑节能设计标准》中则为普通办公室0.25人/m2、高档办公室0.125人/m2[27]。因此本文在模拟时参考软件推荐设置,取人员密度分布为D~N(0.16,0.052),取值区间为[0.10人/m2,0.25人/m2]。
4 运行能耗不确定性量化分析
依据第2章建立的建筑模型,输入第3章所确定的变量分布,应用DesignBuilder的Optimisation+UA/SA模块进行相关设置,采用random抽样法。目前尚无统一的抽样次数计算方法,抽样次数更多依赖于所研究的对象及实际经验。对于本文采用的抽样方法,软件推荐最少抽样次数为变量总数的20倍,即以120次抽样计算,本文计算时设置为200次,满足最少样本次数要求。计算所得多联机运行能耗统计及累积概率分布如图10所示。
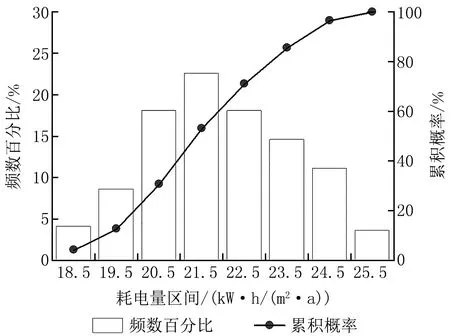
图10 运行能耗统计及累积概率分布
由图10可知,当累积概率取95%时,该建筑空调系统全年单位面积运行能耗为25 kW·h/(m2·a);而单位面积能耗低于20 kW·h/(m2·a)的累积概率则为16.5%。能耗数据的分位数图示法如图11所示。由图11可以看出,各观察值数据基本在一条直线上,可以认为空调系统运行能耗数据符合正态分布。
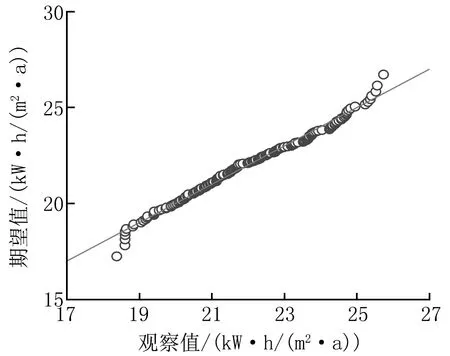
图11 HVAC能耗数据正态性检验
5 变量敏感性分析
分别对空调能耗和供暖能耗进行敏感性分析,用敏感度系数表征能耗对各不确定性变量的敏感程度,其定义式为
(11)
式中λi为能耗相对于变量xi的敏感度系数;ΔE/E为不确定性变量变化时,能耗的相应变化率;Δxi/xi为不确定性变量的变化率。
影响空调能耗的各变量回归系数计算结果如表3所示。

表3 空调制冷能耗不确定性变量回归系数
取空调制冷能耗平均值作为零点,绘制空调制冷能耗各因素敏感性分析图,如图12所示。
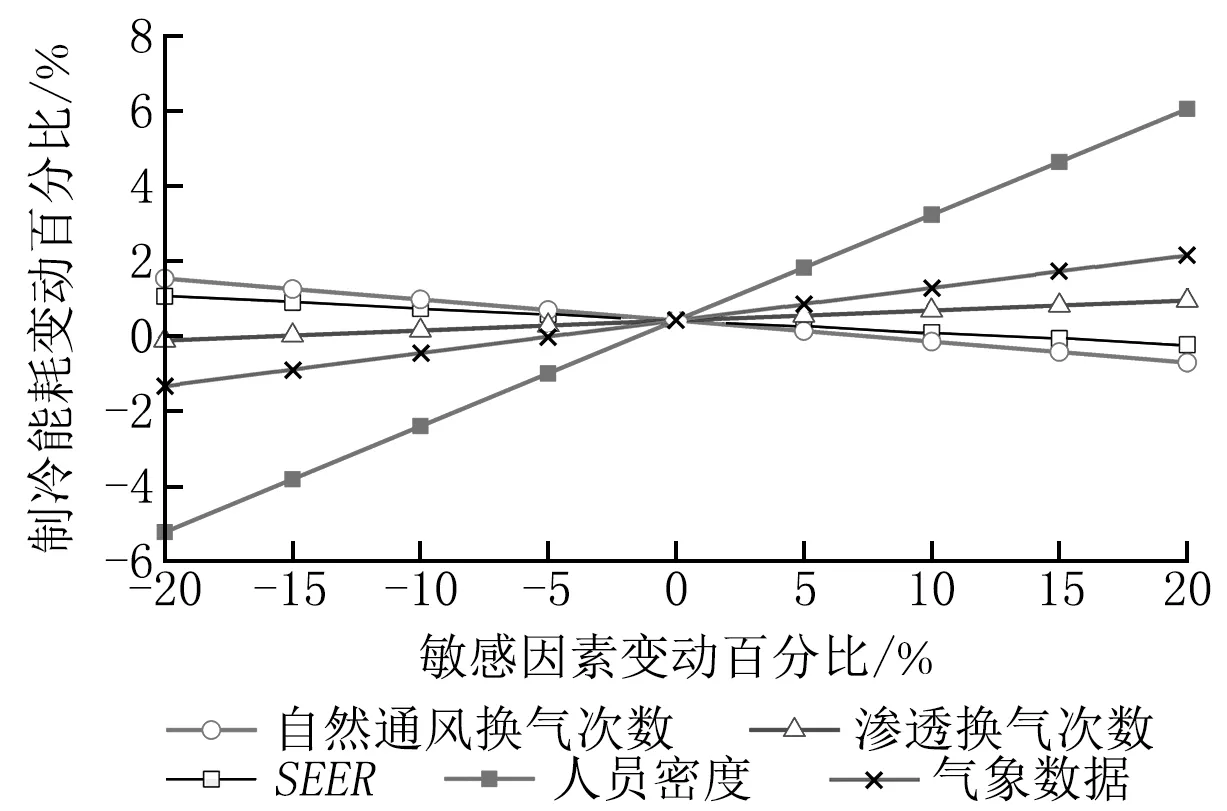
图12 空调制冷能耗敏感性分析图
由图12可以看出,对于本文研究的目标建筑,其空调制冷能耗最为敏感的影响因素是人员密度,其次为自然通风换气次数,相对最不敏感的因素为渗透换气次数。因此合理应用自然通风运行策略,能有效降低空调制冷运行能耗。
影响空调制热能耗的各变量回归系数计算结果如表4所示。

表4 空调制热能耗不确定性变量回归系数
制热能耗影响因素敏感性分析方法与空调制冷能耗的处理方法类似,敏感性因素分析图如图13所示。由图可知,最为敏感的影响因素是气象数据,其次是渗透换气次数。
6 结论
1) 对影响空调运行能耗的输入变量进行辨析,针对不同变量分别确定了参数分布与取值范围。
2) 经不确定性量化分析,当累积概率取95%时,该建筑空调系统全年单位面积运行能耗为25 kW·h/(m2·a);而单位面积运行能耗低于20 kW·h/(m2·a)的累积概率为16.5%。
3) 敏感性分析表明,空调制冷能耗最敏感的影响因素是人员密度,其次是自然通风换气次数;而空调制热能耗最为敏感的影响因素是气象数据,其次为渗透换气次数。
