破片战斗部杀伤面积影响规律研究
2021-06-02李文彬
洪 豆,郑 宇,李文彬,姜 宁
(南京理工大学 智能弹药技术国防重点学科实验室, 南京 210094)
杀爆战斗部是最常见、最主要的战斗部,这种战斗部是利用爆炸后产生的破片与冲击波对目标进行毁伤的。破片杀伤效应是指战斗部爆炸后形成的破片对目标的破坏作用。破片杀伤效应与战斗部爆炸后形成破片的特性参数、目标特性和弹目交汇的条件有关。破片特性参数包括破片数量、破片初速、破片质量分布和空间分布等[1]。杀伤面积作为杀爆战斗部威力的一个重要评判标准,落速、落角和炸高的改变都对其有一定的影响。软件仿真、编程计算等技术的发展使得武器的研制难度和周期得以大大缩短,杀爆战斗部威力场的研究一直都备受关注,在仿真软件未普及之前,对地面目标的杀伤威力计算最核心的问题是求出破片杀伤的等概率曲线[2]。李景云[3]首次提出用等概率曲线来计算杀伤面积,通过实验得到的实验结果与计算结果符合较好。赵丽俊等[4]对立姿人员、卧姿人员和轻型装甲车辆等目标的毁伤幅员进行了分析和计算,得出不同情况下的最佳炸高。李卫平等[5]通过分析破片的飞行特性及空间分布规律,建立了杀爆战斗部杀伤威力计算模型,得出了破片场的破片密度及杀伤概率分布规律,并确定了不同落角情况下的最佳爆高值。刘彦等[6]、马艳丽[7]、李超[8]研究了杀爆战斗部对一些典型目标的毁伤效能。
本文以杀爆战斗部中的预制破片战斗部为研究对象,通过数值模拟和公式预测的方法,得到战斗部静爆下破片飞散特性参数,并在一定的落速、落角和炸高下,计算出动态破片威力场的分布规律,以及破片对人员的杀伤面积,从而研究不同的落速、落角和炸高对破片在地面分布的影响。传统杀伤面积的计算是通过等杀伤概率曲线的方法得到的,即通过杀伤概率加权计算出的加权面积,并不是炸点附近地面上的一块真实的面积。本文中的杀伤面积,是通过有效破片打击目标后,得到的真实杀伤面积,并且能得出破片在地面上的分布图。
1 破片飞散特性及空间分布规律
破片散特性及空间分布规律包括破片初速、破片速度衰减特性、破片飞散角以及破片在飞散角内的飞散分布规律。
1.1 战斗部破片初速
Gurney公式是工程上计算破片初速的常用公式,在其基础上进行修正,得到破片沿轴向的速度分布,其表达式为[9]:
(1)
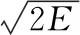
1.2 破片速度衰减特性
破片在飞散过程中由于空气阻力的影响,其速度按指数衰减[1],即:
(2)
式(2)中:Cx为阻力系数;K为破片形状系数;mf为破片质量(kg);ρair为当地空气密度;对于球形预制破片,Cx=0.97,K=3.079×10-3m2/kg2/3,ρair=1.226 kg/m3。
1.3 破片飞散角
计算预制破片战斗部飞散角,首先计算预制破片战斗部两端但每枚破片的飞散方向角,单枚破片的飞散方向角,单枚破片的飞散方向角用修正Shapiro公式进行计算[9],即:
(3)
式(3)中:φ为破片速度矢量偏离壳体法线的偏角;Φ1为战斗部壳体的法线与弹体对称轴构成的夹角;Φ2为爆轰波阵面法线与弹体对称轴构成的夹角;De为炸药的爆速。
1.4 破片空间分布规律
根据弹丸静爆破片飞散试验可得,破片沿弹丸周向均匀飞散,故破片飞散规律与周向角θ无关,沿轴向角φ的飞散呈正态分布[10],即:
(4)
(5)
1.5 破片动态飞散特性
弹丸在空中飞行过程中爆炸,自身具有一定的速度,即落速。落速与破片静爆初速矢量相加即为破片动爆初速,如图1所示[4]。
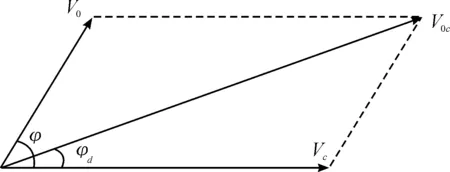
图1 破片速度合成示意图
破片速度和单枚破片的飞散方向角在动态下的计算公式为:
(6)
(7)
式(6)~(7)中:φd为破片动态飞散方向角;V0c为破片动爆初速。
2 数值模拟及分析
2.1 战斗部仿真模型及材料参数
战斗部仿真模型如图2所示,主要由预制破片、炸药和空气组成。战斗部长400 mm,直径200 mm,预制破片直径4 mm,共100层,每层304个。使用ALE流固耦合的计算方法,起爆方式为底部中心单点起爆。
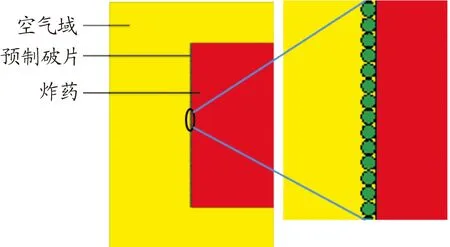
图2 战斗部仿真模型
仿真模型中所使用的材料参数[11-13]:炸药使用B炸药,密度为ρ=1.717 g/cm3,爆速De=7 980 m/s,爆压PCJ=29.5 GPa,其他材料主要参数如表1所示。
采用*MAT_HIGH_EXPLOSIVE_BURN模型以及*EOS_JWL状态方程来定义;预制破片采用钨合金,由于钨球在炸药驱动下,变形程度较小,所以采用*MAT_ELASTIC模型;空气采用*MAT_NULL模型[14-15]。

表1 各材料主要参数
2.2 破片初速分布规律
从上到下依次选取每层一个破片,并给其编号,研究其破片飞散情况,如图3所示。
图3 预制破片选取示意图
炸药起爆后,预制破片在不同时间点上的飞散情况如图4所示。
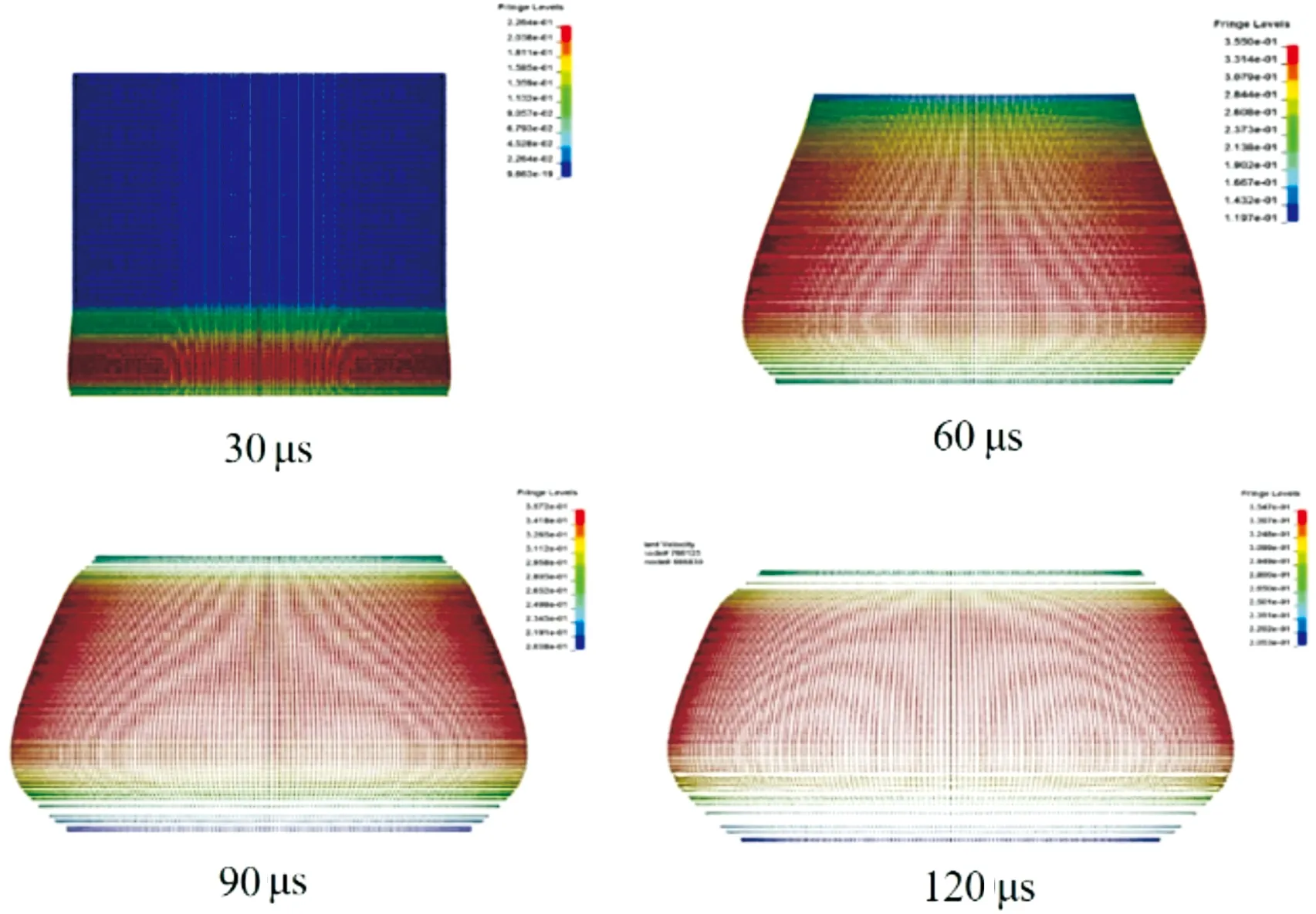
图4 破片飞散空间分布随时间的变化过程示意图
由图4可知,炸药底端中心起爆后,破片沿周向飞散均匀,在战斗部中部速度较高,战斗部两端速度较低。所选破片速度沿轴向的变化情况如图5所示。
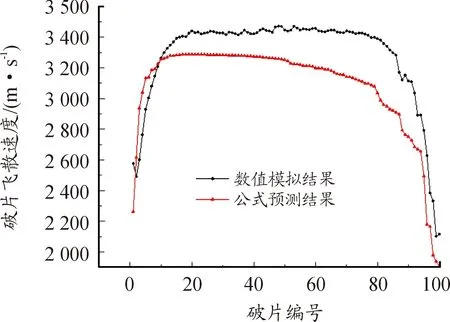
图5 破片飞散速度沿轴向分布曲线
由图5可知,破片在90 μs处速度趋向稳定,最大速度为3 572 m/s,最低速度为2 115 m/s。如图5所示,破片飞散速度沿轴向分布是先增大、中间段趋于稳定、然后再减小。通过式(1)计算得最高速度为3 288 m/s,最低速度为1 904 m/s。
2.3 破片飞散角及飞散方向
破片飞散方向角计算公式为[16-17]:
(8)
式(8)中:φ为破片飞散方向角(°);vz为破片初速轴线方向分量(m/s);v为破片初速(m/s)。
数值仿真得到破片飞散方向角在61°到114°之间,除去个别破片过大或过小的飞散角度,取90%破片进行飞散角计算,破片飞散方向角在73°左右到94°左右之间,破片飞散角为21°。根据公式计算可得,破片飞散方向角在79°到102°之间,破片飞散角为23°。破片飞散方向角的分布曲线如图6。
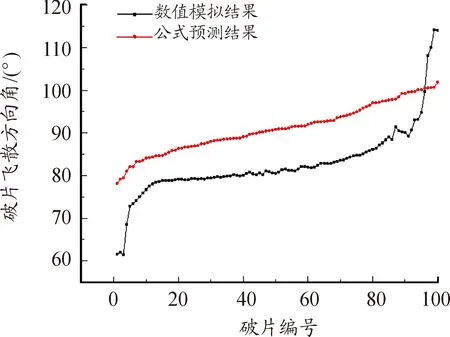
图6 破片飞散方向角的分布曲线
根据图6所示,数值模拟和公式计算的破片初速、破片飞散角的对比结果误差在8%以内,两者较为吻合,数值模拟计算模型具有一定的可行性。
3 战斗部动态破片威力场分布规律
在对破片飞散特性及空间分布规律进行研究的基础上,研究落角、炸高和落速对破片杀伤面积的影响。从公式计算角度出发,需要使用破片飞散公式,再通过蒙特卡洛算法得到每个破片的飞散速度和方向等信息。从仿真计算角度出发,需要通过LS-PREPOST软件观察LS-DYNA计算结果,并提取关注时刻的节点、单元信息,并自编程把节点、单元信息整合出每个破片的速度、飞散方向等信息。运用公式计算和数值模拟得到破片飞散信息后,再基于MATLAB自编程给破片赋予一定的落速、落角,计算出破片在地面上的分布图[18]。
3.1 落角对破片分布规律的影响
在战斗部初速vc=800 m/s,炸高H=10 m时,改变落角θc状态,分别为0°、10°、30°、50°、70°和80°,图7为战斗部与地面交汇示意图,破片在地面上的分布如表2所示。由表2可知,随着战斗部落角增加,破片分布图由两边扩散变到向中间收拢合成一个圆形,且破片密度由密集到稀疏再到密集。
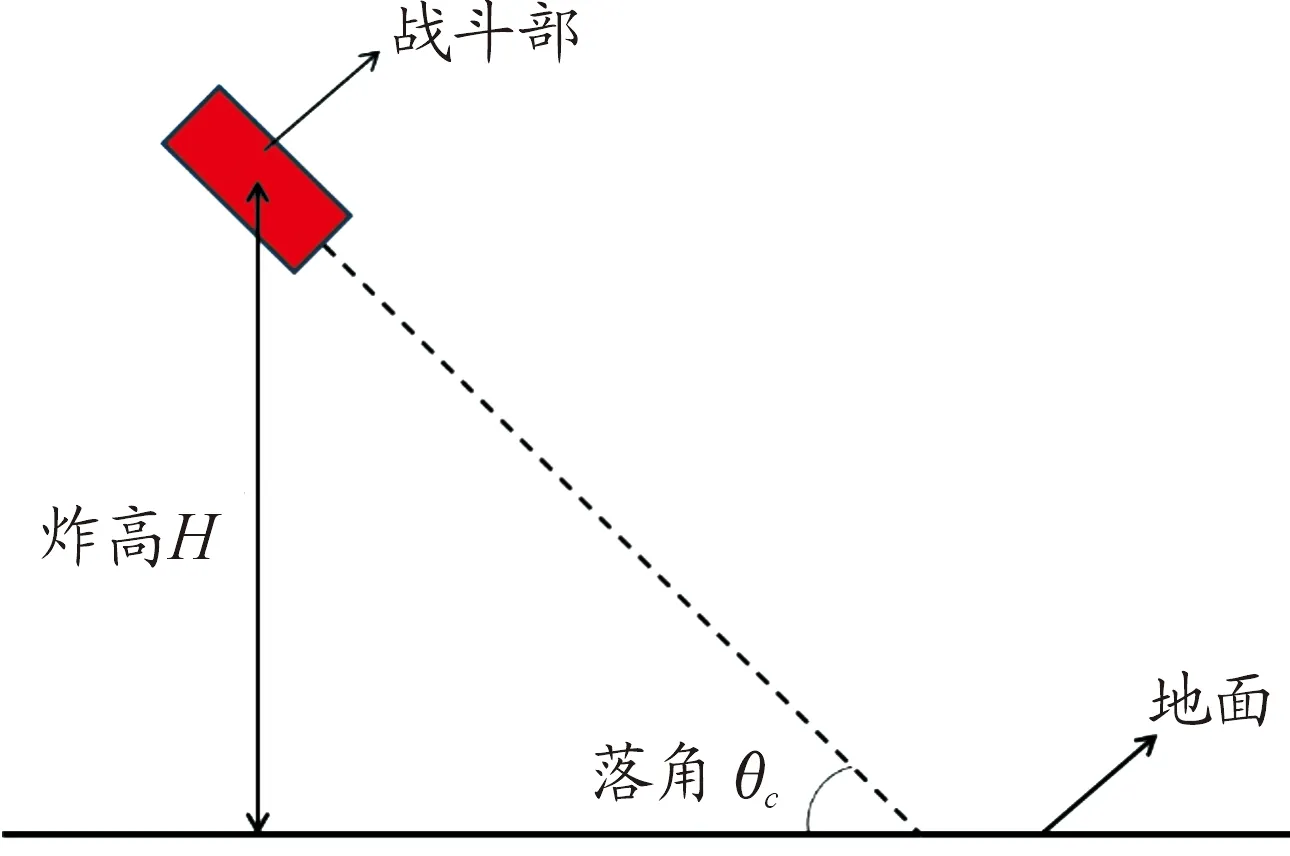
图7 战斗部与地面交汇示意图
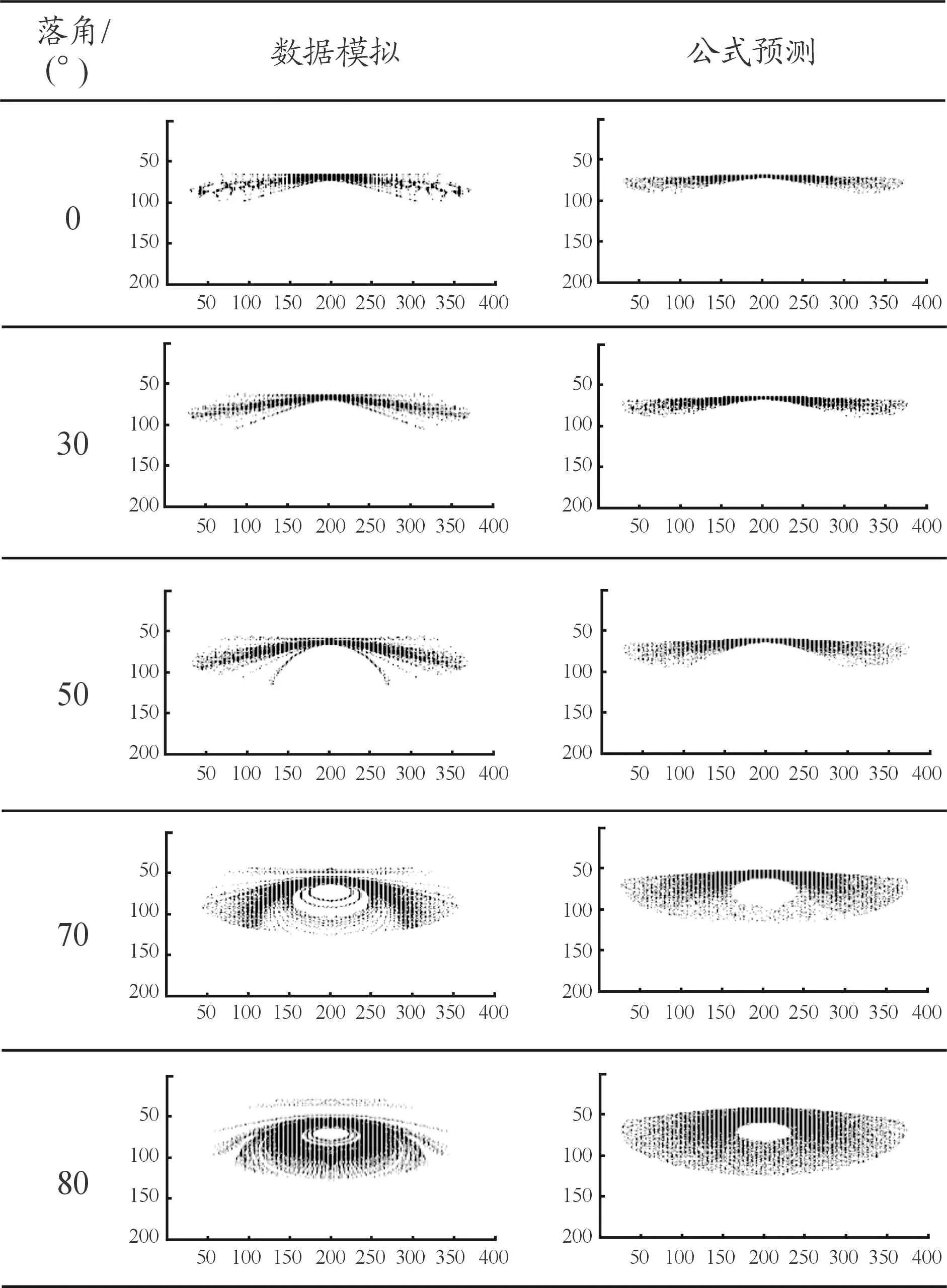
表2 不同落角下动态破片与地面交汇分布
不同落角下的破片杀伤面积如表3所示。杀伤面积计算准则:若0.5 m2(人员站立时的暴露面积)范围内有1枚动能超过78 J的破片,则此面积为杀伤面积。
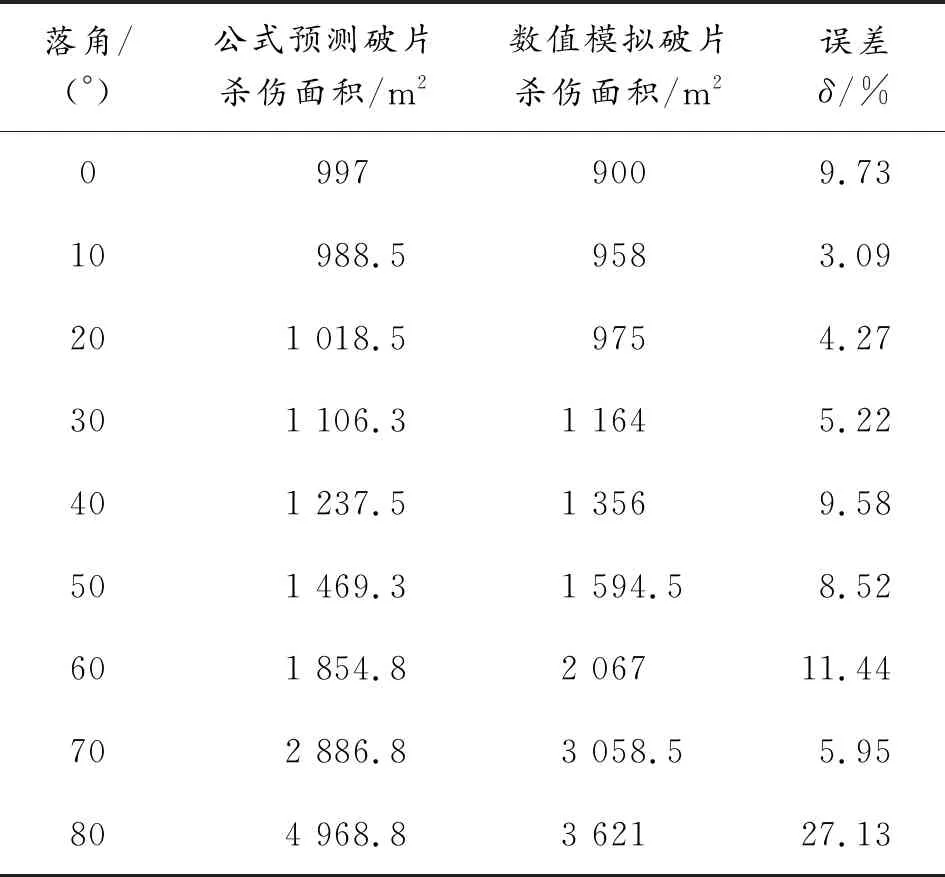
表3 vc=800 m/s, H=10 m不同落角下的破片杀伤面积
由此可得,在战斗部初速vc=800 m/s,炸高H=10 m时,公式预测、数值模拟2种方法计算下,杀伤面积随落角的增大而增大。且在0°~60°之间上升的幅度较小,60°~80°间的上升幅度显著增大。且在小落角下2种方法计算出的杀伤面积较为吻合,大落角下误差较大,这是由于公式预测计算杀伤面积时,使用的蒙特卡洛算法,破片随机分布,在地面上散布区域越大、误差越大。

图8 不同落角下杀伤面积改变曲线
3.2 落角、落速和炸高对杀伤面积的综合影响
根据图9和图10可看出,单一的落速和炸高的变化对杀伤面积的影响较小,故对落角、落速和炸高这3个影响因素进行统一分析。θc=70°、H=10 m时不同落速下的破片杀伤面积如表4所示。θc=70°、vc=800 m/s时不同炸高下的破片杀伤面积如表5所示。
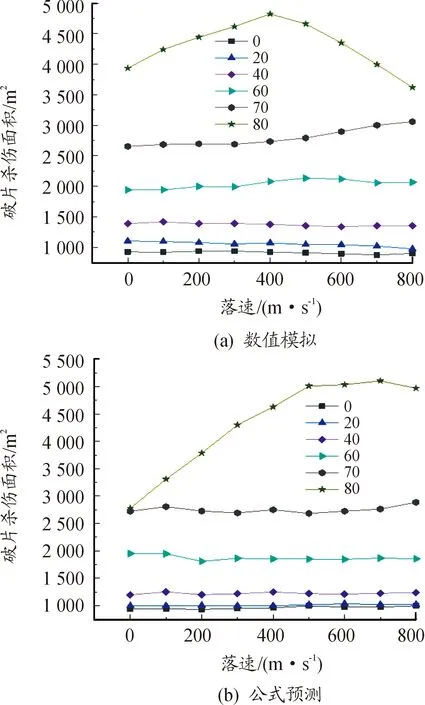
图9 H=10 m时,不同落角下落速对杀伤面积影响曲线
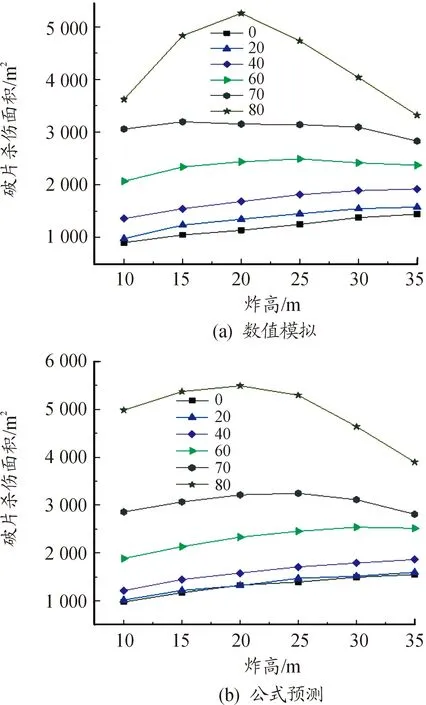
图10 vc=800m/s时,不同落角下炸高对杀伤面积影响曲线
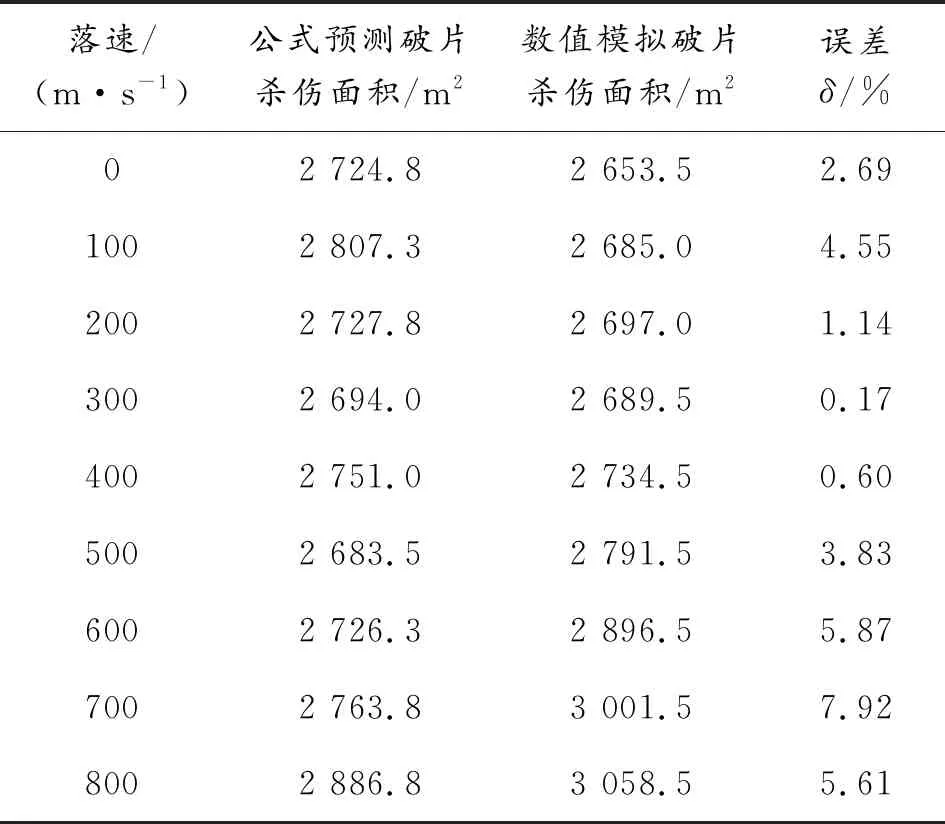
表4 θc=70°, H=10 m时不同落速下的破片杀伤面积
从表4中可以看出,随着落速的变化,公式预测下的破片杀伤面积和数值模拟下的破片杀伤面积吻合性较好,误差在10%以内。从图9可以看出,破片杀伤面积随落速的增加,落角处于0°~70°之间时变化幅度较小,落角到80°时,杀伤面积随落角的增加,先增大后减小。
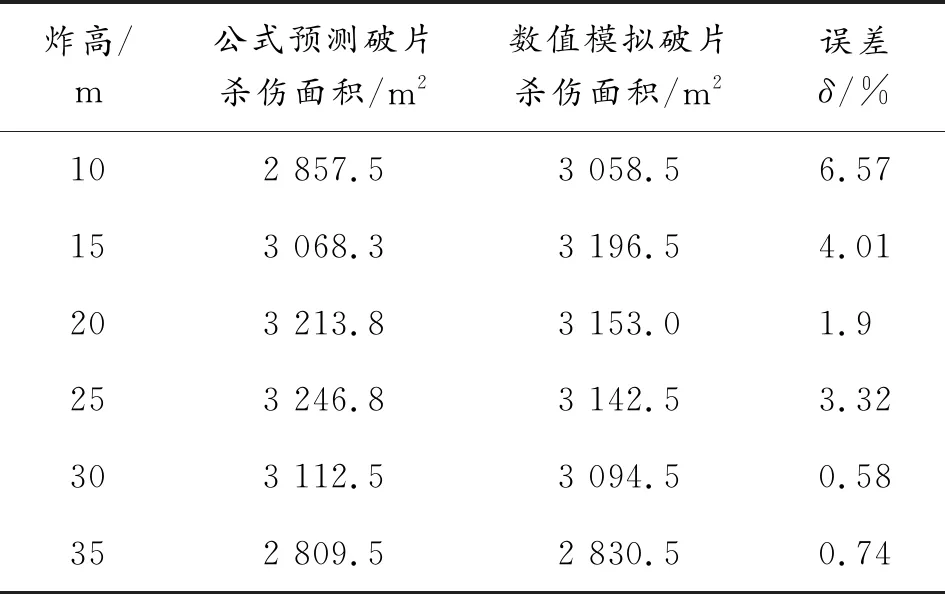
表5 θc=70°, vc=800 m/s时不同炸高下的破片杀伤面积
从表5可以看出,随着炸高的增大,杀伤面积呈现先增加后减小的趋势,且公式预测下的破片杀伤面积和数值模拟下的破片杀伤面积吻合性也较好,误差在10%以内。
从图10可以看出,杀伤面积随炸高的增大,先增加后减小的现象,落角越大越明显。数值模拟得到的数据显示,在落角为70°、80°时,最佳炸高在20 m左右;在落角为60°时,最佳炸高在25 m左右;在落角为40°时,最佳炸高在30 m左右。因此,随着落角的增大,最佳炸高呈现减小的趋势。公式预测得到的数据,也可发现具有同样的规律。
综合上述分析,在落角0°~70°之间,数值模拟和公式预测得到的杀伤面积都不随落速的增大而有规律性的变化,会随着炸高的增大,先增加后减小,但是变化幅度较小。当落角在80°时,在炸高和落速增大时,破片杀伤面积会有明显规律性变化,即先增加后减小。
4 结论
1) 数值模拟和公式预测得到破片在地面的分布图具有较高的一致性,两者得出的破片杀伤面积吻合性较好;战斗部动态破片场分布主要受落角的影响较大,受炸高和落速的影响整体较小。
2) 随着战斗部落角增加,破片分布图由两边扩散变化到向中间收拢合成一个圆形;除去大落角下引起的杀伤面积计算误差,破片杀伤面积随落角的增大而增大;随炸高的增大,先增大后减小。
3) 除去80°大落角时的计算误差,对于本文研究的预制破片战斗部,其最优落速、落角和炸高的组合应为(800 m/s,70°,20 m)。
