基于列车制动功率的地面式储能系统阈值优化研究*

董礼玮 王之琪 胡景泰 梁海泉 左建勇

(同济大学铁道与城市轨道交通研究院， 201804， 上海∥第一作者， 硕士研究生)

超级电容器具有功率密度大、充放电速度快、循环寿命长、效率高等优点[1-2]，因此适用于回收地铁车辆在频繁启停过程中产生的大量再生制动能量[3]。对储能系统的工作阈值进行优化通常可实现更好的能量管理效果。文献[4]在考虑线路阻抗和变电所非理想空载输出状态的基础上，提出了设置动态阈值提高储能系统工作性能的控制方法。文献[5]提出了基于空载电压和SOC(荷电状态)的动态阈值控制方法，用于改善牵引网空载电压波动对储能装置的影响。文献[6]研究了包括制动电阻启动电压、储能装置吸收阈值等因素在内的多目标优化，成功地提高了整体节能率。

本文考虑制动能量的线路阻抗损耗，推导了储能系统充电阈值与能量回收率的关系，验证了通过提高储能系统充电阈值降低能量损耗的可行性。为了保证受电弓处网压处于正常工作范围，同时最大限度提高能量回收率，对制动电阻工作阈值进行了优化研究。在此基础上，提出了一种根据列车最大制动回馈功率的储能系统和制动电阻工作阈值优化方法。最后通过仿真，分别在单车制动和多车制动工况下对该阈值优化方法的有效性进行了验证。

1 储能系统结构及控制策略

1.1 储能系统结构

地铁的地面式再生制动储能系统由双向DC/DC变换器和超级电容储能装置两部分组成，如图1所示。其中，双向DC/DC变换器由降压斩波(Buck)电路和升压斩波(Boost)电路两部分组成。在Buck模式下，能量从直流电网流向储能装置，储能装置处于充电状态；在Boost模式下，能量由储能装置流向直流电网，储能装置处于放电状态。

1.2 储能系统控制策略

直流牵引网电压变化能够直接反映列车运行状态，因此本文采用以牵引变电所出口处网压为控制对象的经典双闭环控制策略，其控制框图如图2所示。该控制策略通过检测牵引变电所出口处网压Usub作为反馈，与储能系统的充电阈值Uch或者放电阈值Udis进行比较，经PI(比例积分)调节器输出储能装置充放电电流参考值Isc_ref；再将测得储能装置电流实际值Isc与参考值之差，经PI调节器输出直流变换器的开关占空比；根据占空比生成变换器开关PWM(脉冲宽度调制)信号，实现降压/升压的调节。此外，引入超级电容SOC对充放电电流进行限制，以避免储能装置过充和深度放电。

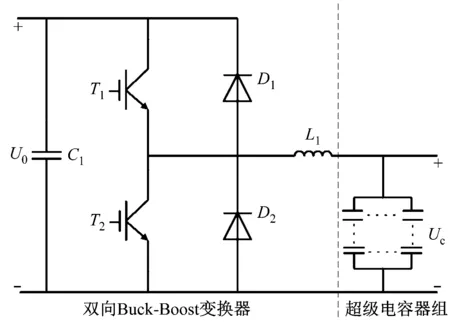
图1 地面式再生制动储能系统结构

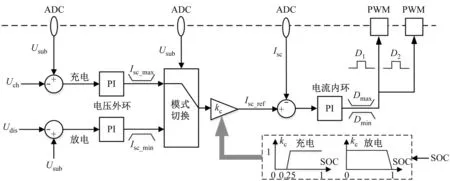
图2 地面式再生制动储能系统控制框图

2 储能系统阈值优化分析

制动能量由车辆向储能系统传输的过程中，有一部分损耗在线路阻抗上。为减少损耗能量，最大限度将其回收是阈值优化的关键。在制动过程中，列车某时刻向牵引网反馈功率为定值，若改变储能系统充电阈值，则牵引变电所出口处网压受控会发生改变，线路上电流随之产生变化，从而影响线路的能量损耗。下面假设储能系统的容量能够完全吸收单列车制动能量，使用广州地铁4号线万胜围站到车陂南站区间实际参数，对储能系统充电阈值与制动能量回收率的关系进行推导。

列车制动回馈功率和线路参数的关系：

Pe=IlineUt

(1)

列车受电弓处网压与储能系统充电阈值的关系：

Ut=Uch1+IlineRΣ

(2)

制动回馈功率在线路上的损耗功率为：

(3)

储能装置的内阻损耗功率为：

(4)

式中：

Pe——列车制动回馈功率；

Iline——牵引网电流；

Ut——列车受电弓处网压；

Uch1——储能系统充电阈值；

RΣ——线路总阻抗，包括接触网阻抗、钢轨阻抗以及受电弓阻抗；

Pline——线路上的损耗功率；

Psclost——储能装置的内阻损耗功率；

Rsc——储能装置等效内阻；

Isc——储能装置工作电流；

Rsc,o——根据储能装置的实际内阻损耗等效到牵引网上的电阻；

k——内阻等效系数，取0.2。

能量回收率η的计算公式为：

(5)

结合式(1)～(5)，并经过化简得到：

(6)

由式(6)可得能量回收率与储能系统充电阈值的关系，如图3所示。由图3可知，能量回收率随着储能系统充电阈值单调递增。在实际控制过程中，储能系统充电阈值在1 500 V往上，此时随着充电阈值增大，能量回收率增长越来越缓慢，最终趋近水平。

图3 储能系统充电阈值与能量回收率关系

储能系统充电阈值越高，能量回收率越大，但若设置过高，当接近制动电阻工作阈值Uch2时会触发制动电阻工作。因此，Uch1的设置应小于Uch2。制动电阻工作阈值的取值决定了储能系统充电阈值的上限，若要最大限度提升能量回收率，制动电阻工作阈值要设置得更高一些。受电弓处网压由于线路阻抗的存在比出口处网压要高，Uch2设定得过高可能会导致再生制动失效。为了避免再生制动失效，同时最大限度提高能量回收率，有必要对制动电阻的工作阈值Uch2设定范围进行研究。

制动电阻工作时受电弓处网压应满足：

Ut=Uch2+IlineRΣ

(7)

Ut≤1 800

(8)

结合式(1)、式(7)和式(8)，可推导出制动电阻工作阈值的取值范围为：

(9)

式中：

Pe，max——最大制动回馈功率；

RΣmax——最大线路总阻抗。

因此，在保证受电弓处网压处于正常工作范围的前提下，使能量回收率最大的Uch1和Uch2取值分别为：

(10)

式中：

ΔU1、ΔU2——取值裕度，取值应分别为储能系统和制动电阻工作时电压波动引起的最大偏差值。

3 仿真验证

为了验证上文的阈值优化分析，将所研究线路区间的参数以及车辆制动功率曲线输入到仿真模型中，对单车制动和多车制动两种工况下分别进行验证。

3.1 单车制动

初始条件下设置储能系统充电阈值为1 500 V，制动电阻工作阈值为1 650 V。在单列车制动的工况下，牵引变电所出口处网压曲线如图4所示，储能装置充电电流与电压如图5所示。

图4 单车制动时牵引变电所出口处网压

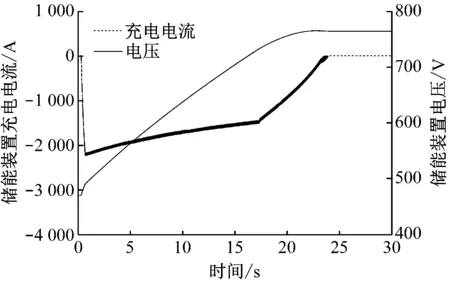
图5 单车制动时储能装置充电电流和电压

由图4可知，牵引变电所出口处网压在整个制动过程都维持在1 500 V左右，波动范围在±1.5%左右，制动能量都被储能系统吸收，制动电阻未启动。根据图5中储能装置的电压变化，计算出再生制动能量回收率为：

(11)

式中：

Es——储能装置吸收能量；

Ef——列车再生制动反馈能量；

C——储能装置等效电容；

Usc——储能装置电压。

根据式(10)，计算出优化的Uch1和Uch2分别为1 670 V、1 690 V，即该阈值配置下能量回收率达到最大。在制动电阻工作阈值Uch2分别为1 650 V和1 690 V的情况下，改变储能系统充电阈值并进行多次仿真，结果如图6所示。由图6可知，当储能系统充电阈值Uch1为1 500～1 630 V时，优化前后的制动能量回收率都随着Uch1的增大呈增长趋势，这与式(6)的推导结果保持一致。当Uch1为1 635 V时，优化前的能量回收率轻微下降，这是因为在控制过程中网压会产生波动，在储能系统充电阈值接近制动电阻工作阈值时，容易触发制动电阻工作，从而消耗了一部分能量，由此也验证了式(10)中留有取值裕度的必要性。随着Uch1继续增大，在制动电阻上消耗的能量变得更多，制动能量回收率迅速下降。而优化后的能量回收率继续增长，在Uch1为1 670 V时达到最大值94.3%，较初始阈值条件下93.2%的能量回收率提高了1.1%。同理，Uch1增长到1 690 V之后，制动能量回收率开始迅速下降。

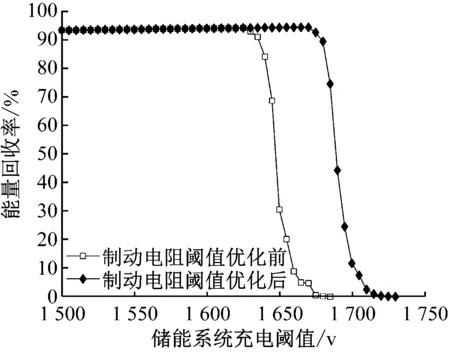
图6 制动电阻阈值优化前后能量回收率

3.2 多车制动

根据所研究区间发车时刻表可知，在制动过程中可能出现最大回馈功率的工况是上下行车辆同时制动。该情况下，制动能量超过储能装置容量，储能装置会提前充满，制动电阻随后开始吸收多余能量。此时阈值优化的主要目的是为了保证列车受电弓处网压不超过临界值，避免再生制动的失效。仍以初始的阈值状态进行仿真，该工况下牵引变电所出口处网压如图7所示，列车受电弓处网压如图8所示。

由图7可知，在第17 s左右，牵引变电所出口处网压由1 500 V上升到1 650 V，此时储能装置处于过充状态，在SOC限流控制下已停止工作，制动电阻投入工作吸收多余制动能量。由图8可知：在第17 s之前，储能装置工作时，列车受电弓处网压都维持在正常的工作电压范围内；第17 s之后，制动电阻投入工作，受电弓处网压在一段时间内超过了1 800 V，导致再生制动的失效。根据式(10)进行制动电阻工作阈值优化，将制动电阻工作阈值Uch2设为1 550 V，储能系统充电阈值Uch1设为1 530 V，阈值优化后的列车受电弓处网压如图9所示。

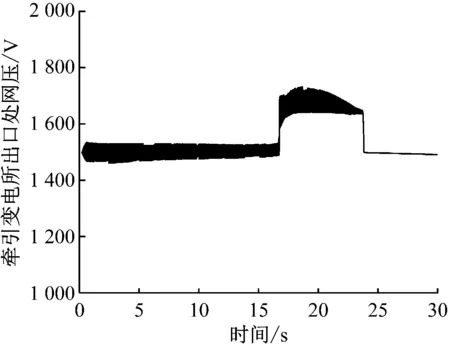
图7 多车制动时牵引变电所出口处网压

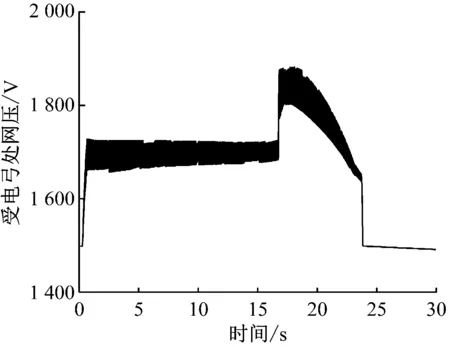
图8 多车制动时列车受电弓处网压

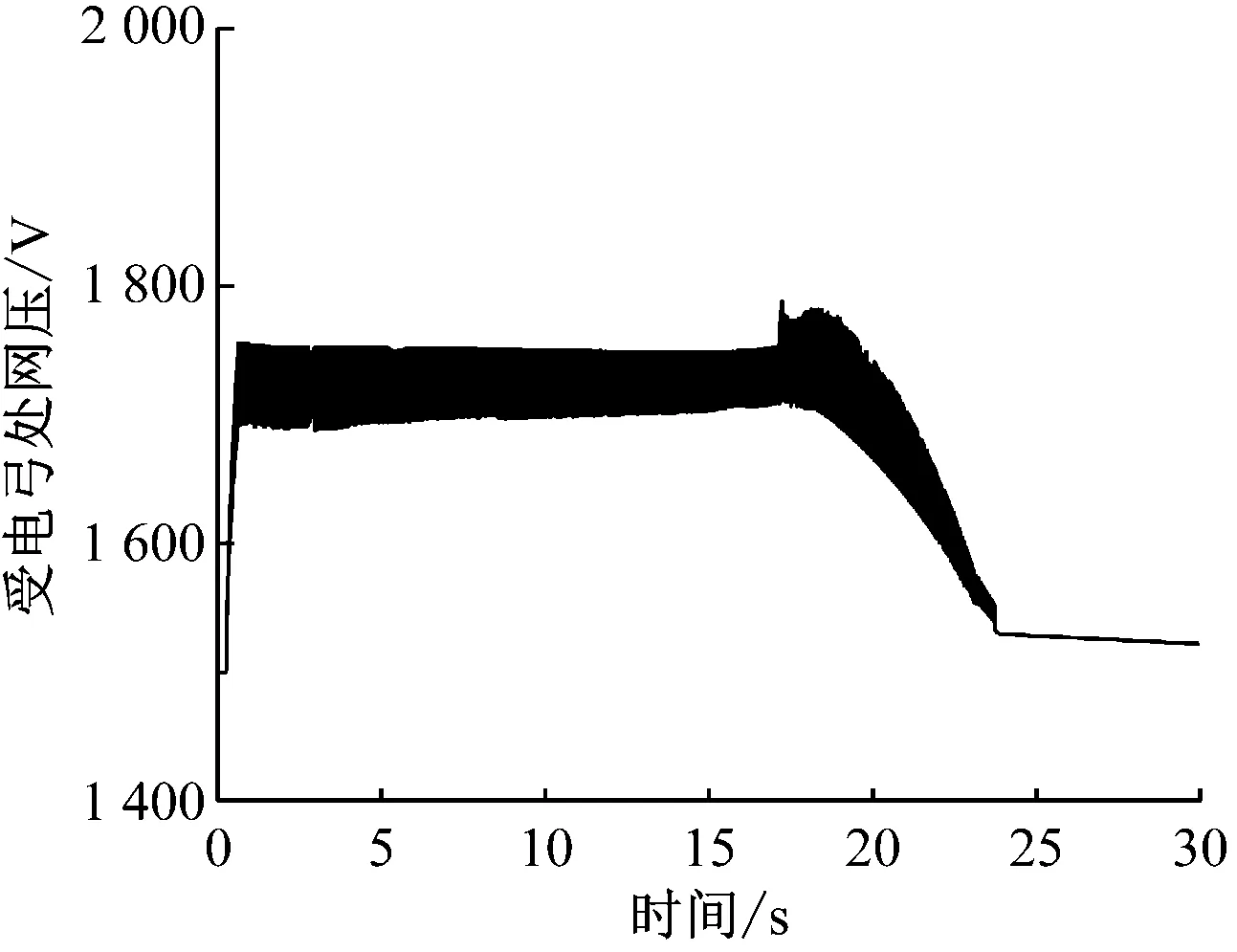
图9 阈值优化后多车制动时列车受电弓处网压

由图9可知，阈值优化后，列车受电弓处网压始终控制在1 800 V以下，避免了再生制动失效情况的发生，从而验证了阈值优化的有效性。

4 结语

本文以降低再生制动能量的线路损耗与稳定列车受电弓处网压为目标，提出了一种储能系统和制动电阻联合工作时的阈值优化方法。仿真结果表明：在单车制动时，该方法能够有效地提高再生制动能量回收率，较初始的阈值状态能量回收率提高了1.1%，从长期来看可以带来可观的经济效益；在多车制动时，列车受电弓处网压始终维持在1 800 V以下，可避免再生制动失效情况的发生。