轨道交通引起的地面高层建筑室内振动分析

叶 玮 张海峰 毛 刚 鲍侃袁 徐志广

(1.杭州北和置业有限公司， 310022， 杭州； 2. 京投科技(北京)有限公司， 101300， 北京；3.杭州园林设计院股份有限公司， 310012， 杭州； 4. 西安卓控环保科技有限公司， 710005， 西安∥第一作者， 高级工程师)

在我国，建设环境友好型城市和集约高效利用土地的城市建设方针，要求对轨道交通沿线土地进行综合开发和高效利用，因此轨道沿线土地开发利用是解决城市轨道交通发展、城市用地稀缺的必由之路。在沿线物业开发与轨道交通同步规划的过程中，轨道交通可能带来的振动噪声问题不容忽视，长期以来是政府环保部门关心的关键问题。开展振动噪声控制专项研究工作，进行准确的振动预测和制定合理可行的振动噪声解决方案，对于我国各大城市的城市轨道交通综合发展具有重要意义。

近年来，很多学者关注到了轨道交通对地面建筑物的振动噪声问题并进行了大量研究。在振动噪声预测及传播规律研究方面，袁扬等[1]采用不同的锤击材料作为激励源，分析了振动在隧道—地层—建筑物的传递特性。蒋通等[2]通过室内仿真分析和室外现场试验，研究了高架轨道交通引起的环境振动。王晨[3]提出了城市轨道交通高架线路噪声影响简化预测模型，并给出了每种噪声的预测计算公式。在振动控制策略方面，肖翔文[4]立足于城市轨道交通所存在的振动、噪声来源，总结了有针对性的解决策略。涂勤明[5]针对车辆段综合减振降噪技术已形成的系列方案和配套技术进行了研究。

为了进行建筑物室内振动噪声的预测分析，本文选取尚在规划阶段的某项目地块作为研究对象。该项目是城市轨道交通上盖物业综合开发的典型案例，与正在建设中的杭州某地铁线路相邻，两者的相互位置关系如图1所示。其中，线路下穿8号楼、9号楼、12号楼三栋建筑物，且距离其他4栋建筑物的水平距离不足10 m。该地段线路半径为380 m，属于小曲线半径，设计车速为65 km/h，轨道上拟采取的隔振措施为钢弹簧浮置板。

目前，地铁线路正处于建设过程中，尚未通车，建成后的建筑物室内振动是项目开发商、业主和环评部门共同关心的问题。针对这一实际情况，本文分别利用经验公式法和数值仿真法，预测该地段地铁列车运行引起的建筑物室内振动情况。

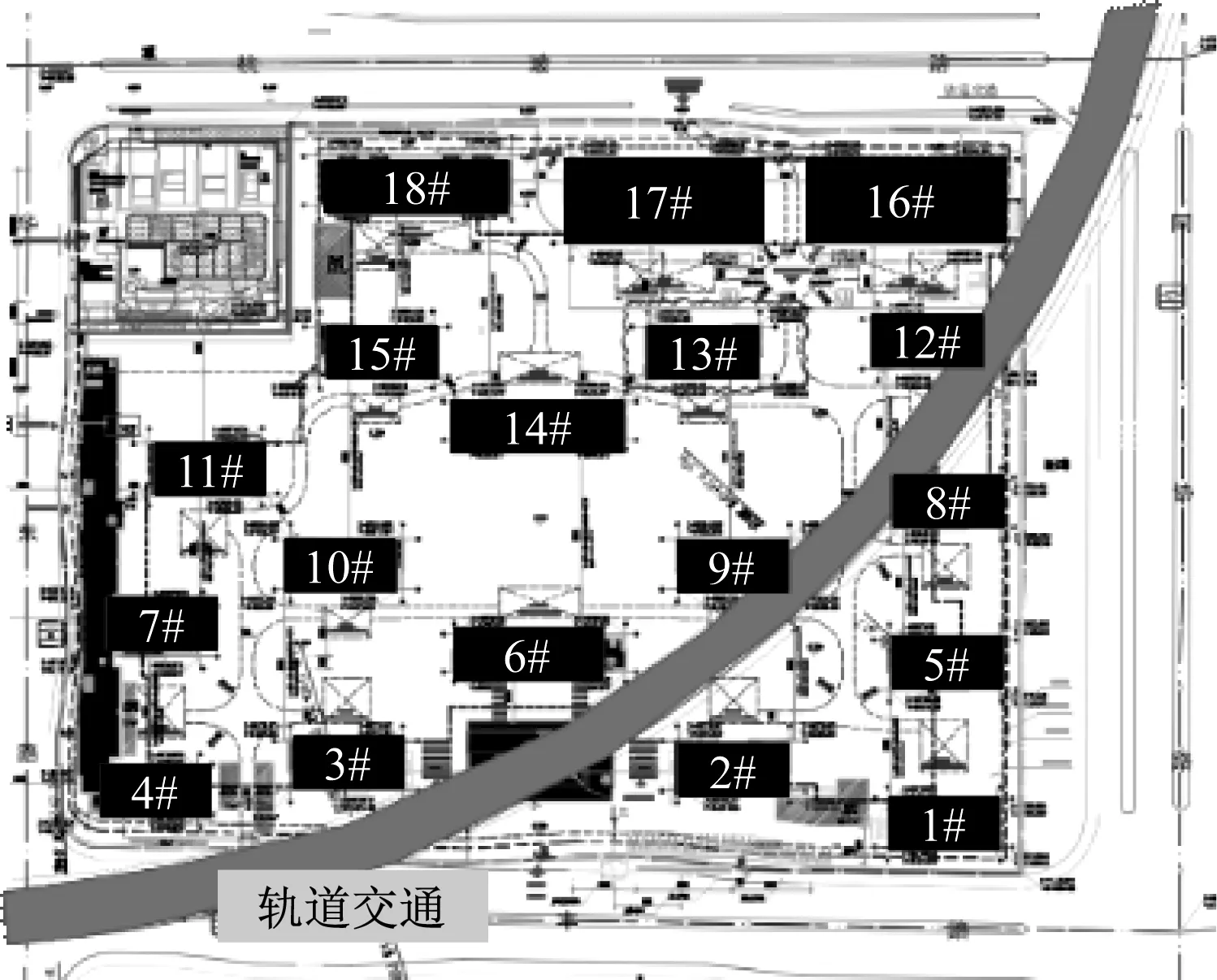
图1 线路与建筑物位置关系图

1 预测方法介绍

振动预测一般采用经验公式法或者数值仿真分析两种方法，其中经验法具有计算简便的优势，而数值仿真法能建立更贴近实际线路和建筑物情况的力学模型。以下分别用预测法和数值仿真法的经验公式对该项目地块的建筑进行振动预测。

1.1 经验法预测原理

建筑物室内振动VLZmax的经验公式为：

VLZmax=VLZmax0+C

(1)

式中：

VLZmax0——列车振动源强，为参考列车通过时段隧道洞壁的参考点Z计权振动级最大值，dB；

C——修正项，C=Cv+Cm+Cc+Cr+Cd+Cb，其中：Cv为车速修正，Cm为轴重和簧下质量修正，Cc为曲线修正，Cr为钢轨条件修正，Cd为距离衰减修正，Cb为建筑物修正。

车速修正Cv、曲线修正Cc和钢轨条件修正Cr的计算方法如表1所示。表中，Cv中匀速状态下的v为列车通过预测断面的运行速度，v0为源强的列车参考速度，v和v0的单位为km/h。Cr条件中，当线路条件为道岔时，根据类比测试合理选取0～10 dB之间的修正量[6]。

Cm用来修正实际运行车辆与源强车辆的质量差异，当车辆轴重和簧下质量与源强车辆不同时，Cm计算公式如下：

Cm=20 lg(W/W0)+20 lg(Wu/Wu0)

(2)

式中：

W0——源强车辆的参考轴质量，t；

W——预测车辆的轴质量，t；

Wu0——源强车辆的参考簧下质量，t；

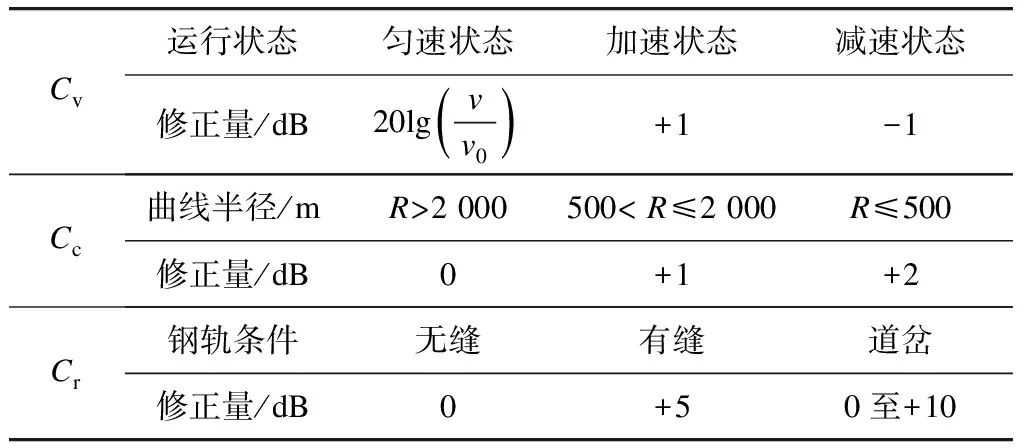
表1 修正项Cv、Cc、Cr的计算

Wu——预测车辆的簧下质量，t。

距离近轨线路中心线50 m范围内，Cd可按如下公式计算：

Cd=-10.9 lgl2+16 lgl-7.5

(3)

式中：

l——预测点至临近线路源强监测点处的直线距离，m。

(4)

式中：

Rv——预测点至临近线路中心线的水平距离，m。

式(3)适用于预测点至轨顶的垂直距离在8～34 m时的距离修正。当预测点至轨顶的垂直距离大于34 m时，Cd需按照HJ453《环境影响评价技术导则 城市轨道交通》[6]中所给出的方法。

根据建筑物的结构及特征差异进行Cb的计算。Cb为敏感建筑物室外环境振动修正量，如表2所示。表中，低层建筑是指1～3层的建筑，多层建筑指4～6层的建筑，中高层建筑指7～9层的建筑，高层建筑指≥10层的建筑。

表2 建筑物修正

根据规范要求，在VLZmax的基础上引入预测误差值±2 dB[7]，最终得到振动预测结果VLZmax,c的区间为：

VLZmax,c=[VLZmax-2 dB，VLZmax+2 dB]

(5)

1.2 数值仿真模型介绍

根据以往实测经验以及研究成果可知，线路下穿时，建筑物的室内振动最大，因此选取城市轨道下穿建筑物的工况作为数值仿真的分析对象。建立地面上某高层建筑的轨道-土层-建筑物的有限元动力学计算模型，如图2所示。根据文献[6]，采用有限元法求解连续介质的振动问题，这会引起低通效应和频散效应，单元尺寸越大，两种效应越明显。为了平衡计算效率和计算结果的精确度，土体的单元尺寸参照文献[7]中的尺寸进行选取，即隧道结构附近的土体采用0.5 m的单元边长，远离隧道结构的土体采用2 m的单元边长。根据《工程场地地震安全性评价工作规范》[8]，有限元单元尺寸不应大于结构动力学问题所考虑最短波长的1/8。地铁引起的周边结构振动频率在200 Hz以内，钢筋混凝土振动频率为200 Hz的剪切波，波长为12 m，因此隧道上方建筑的单元尺寸不能大于1.5 m，根据有限元结构试算，建筑物网格尺寸为0.5 m，根据地勘资料设置5层不同材料属性的土体，模型所用各单元类型及其取值参数如表3和表4所示。

图2 轨道-土层-建筑物整体模型

表3 轨道-土体-建筑物有限元模型单元及参数

表4 扣件和隔振器有限元模型单元及参数

2 经验法计算结果

2.1 振动预测中各修正项计算

首先确定列车振动源强VLZmax0，在《地铁噪声与振动控制规范》[9]附录中，给出了普通整体道床上直线段DT VI2普通扣件的源强值为84 dB。本项目轨道拟采用钢弹簧浮置板隔振措施，该类产品属于特殊减振措施，修正量为-20 dB，则修正后的列车振动源强VLZmax0为64 dB。

然后进行各修正项计算，已知基准车速v0为70 km/h，项目位于线路区间段，本文认为地铁车辆匀速通过，地铁设计车速为65 km/h，按照表1中计算方法可得Cv为-0.5 dB；预测线路上采用地铁B型车，基准源强也为B型车，两者轴重与簧下质量完全一致，无需进行轴重和簧下质量修正；预测线路曲线半径为380 m，则Cr为2 dB；该地段线路使用无缝钢轨，Cr为0；以线路上方某栋建筑物为例，该建筑物标高为-4.6 m，地铁埋深为10 m，属于I类建筑物，根据式(3)可得距离修正Cd为-1.5 dB，参照表2得到其建筑物修正Cb为-3 dB，对于其他建筑物，距离修正和建筑修正计算方法类似，不再赘述。

2.2 各建筑物室内振动预测结果汇总

确定各修正项的取值后，容易计算得到以线路上方某建筑物为例的室内最大振级预测值为61 dB；引入预测误差±2 dB后，最终得出该建筑物的VLZmax预测区间为[59 dB，63 dB]。

实际项目地块上拟建17栋建筑物，各建筑物与轨道交通的水平距离如表5所示。使用2.1节所述方法，对项目地块上所有建筑物进行室内振动预测，所得预测结果汇总如表5所示。

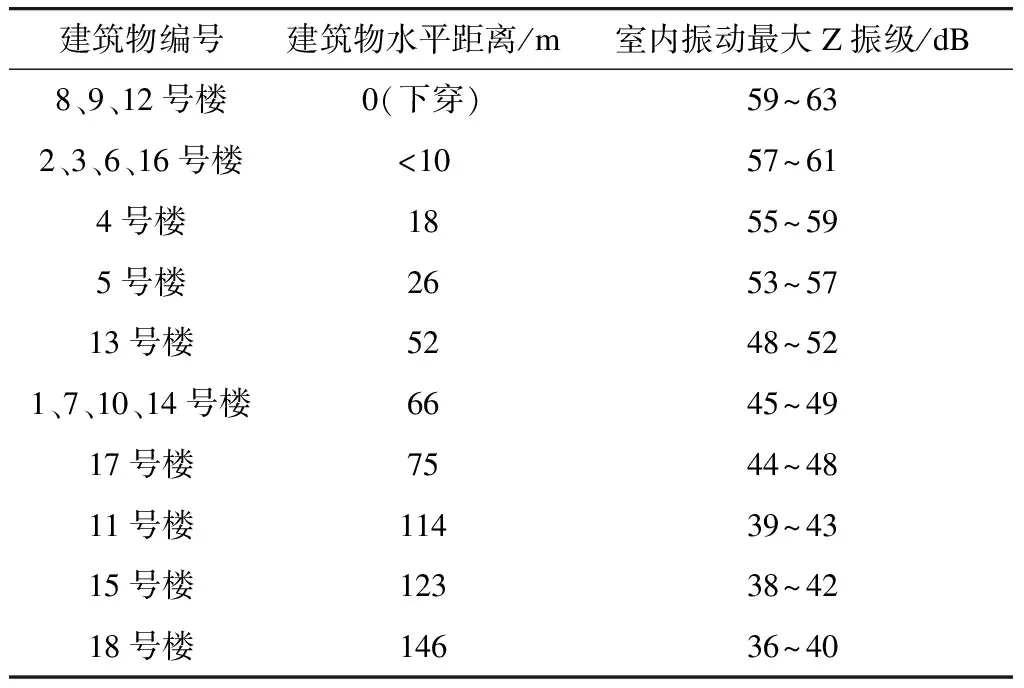
表5 各建筑物振动及二次结构噪声预测结果汇总

计算结果表明，相同水平高度条件下，建筑物离城市轨道线路的水平距离越近，受列车运行的振动影响越大。当线路下穿建筑物时，该楼的室内振动最大；当建筑物与线路的水平距离超过52 m时，建筑物室内振动预测值将低于50 dB。根据以往经验，振动预测值小于50 dB的建筑物，在现场测试时采集数据将以背景振动为主，一般为50～53 dB。

3 有限元法计算结果

3.1 振动加速度计算结果

使用与预测路段运行条件类似的其他已运行线路上的钢弹簧浮置板轮轨力作为输入值，加载到力学分析模型中。观察点位置分别取地铁上方某建筑物的1层、4层、7层、13层及16层的地板中心，观察点示意图如图3所示。

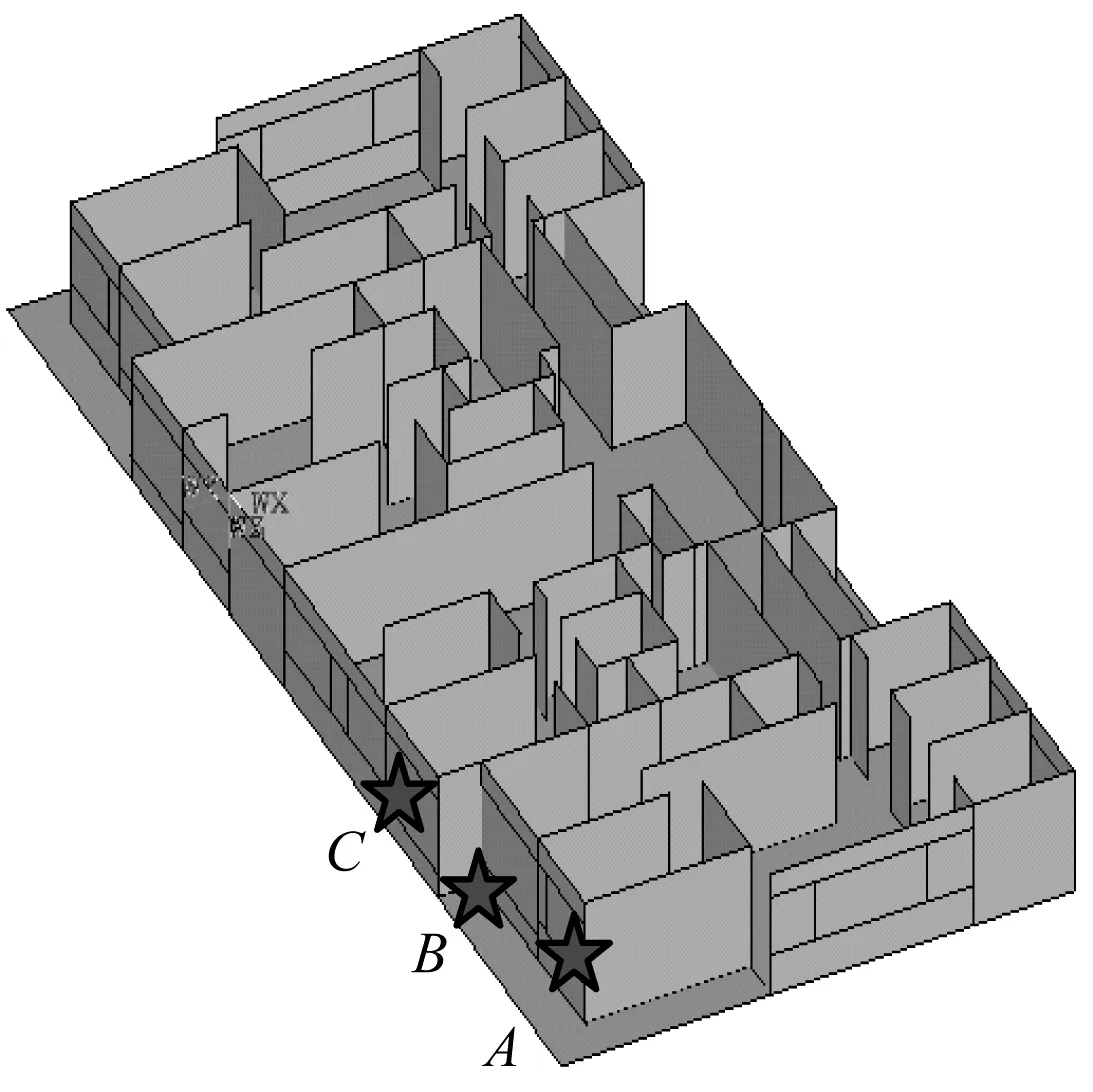
图3 建筑物户型图

通过有限元计算可分别得到各楼层各房间观察点振动加速度时程曲线。该建筑物内各楼层观测点的振动加速度波形时程曲线如图4～图6所示(下文中观测点字母代表房间位置，数字代表楼层，例如A1表示1楼A位置处的观测点)。

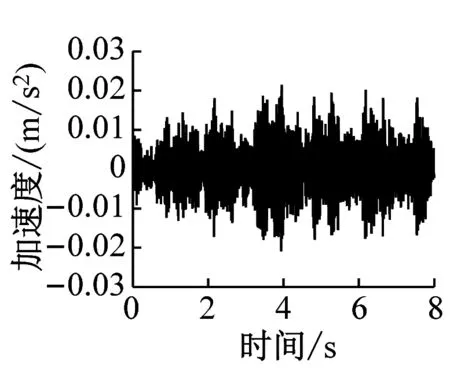
a) A1

b) A4

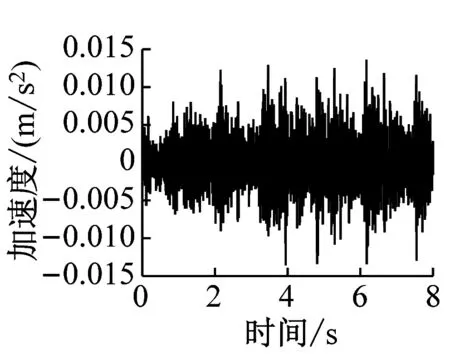
c) A7

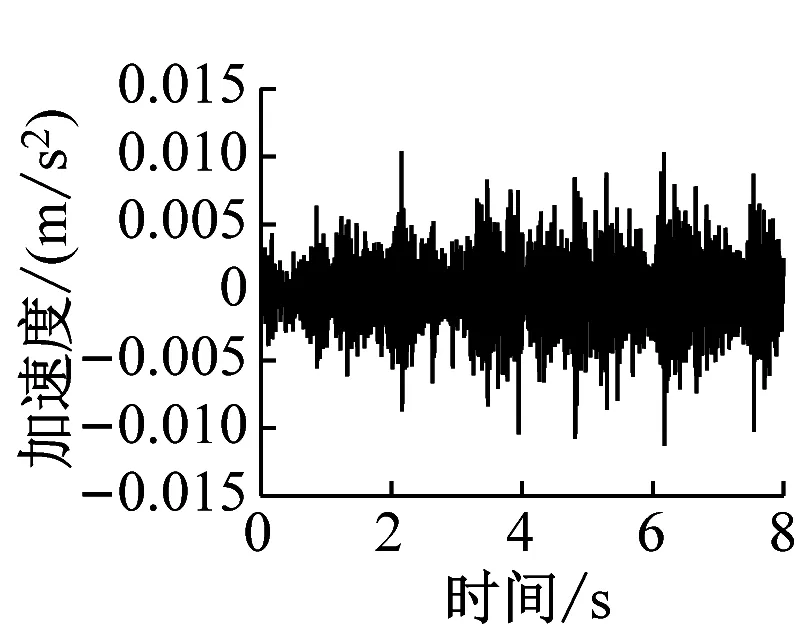
d) A13

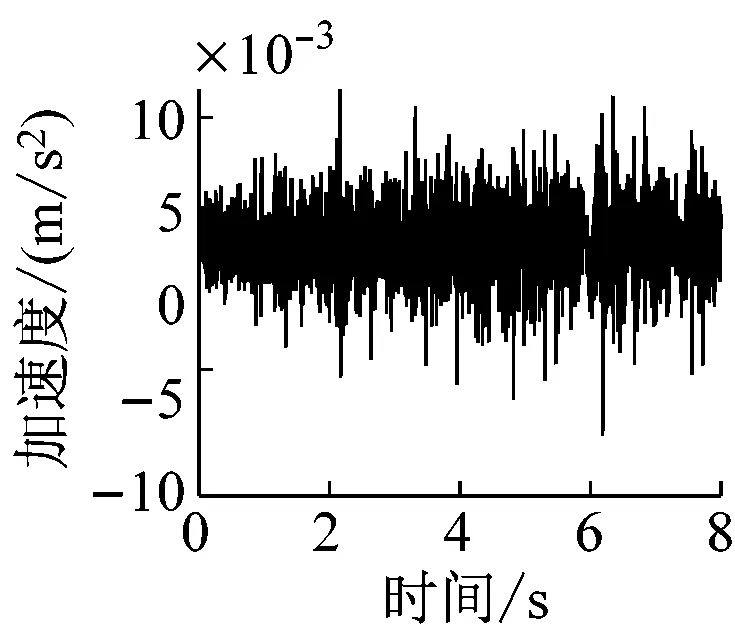
e) A16

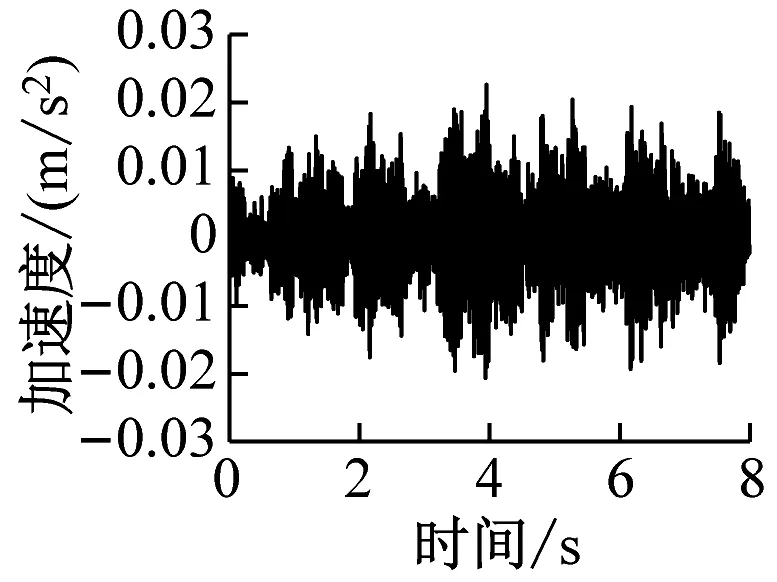
a) B1

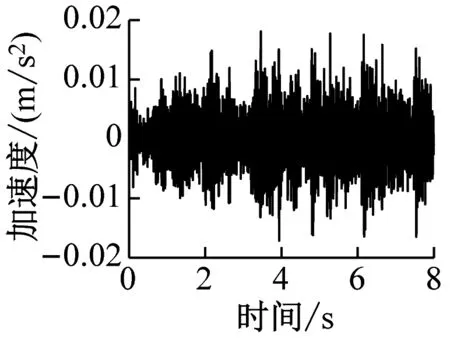
b) B4

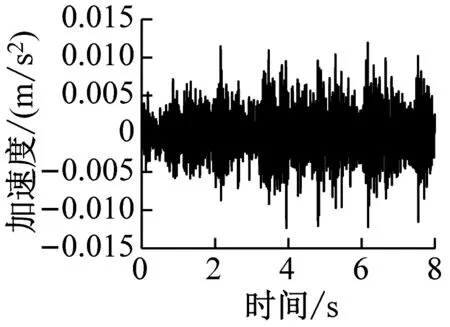
c) B7

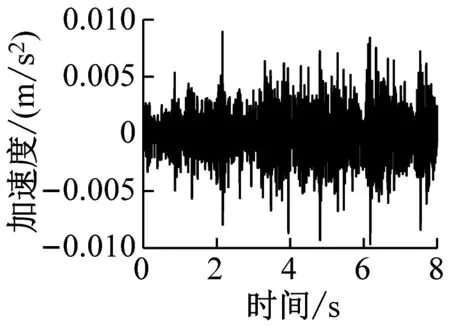
d) B13

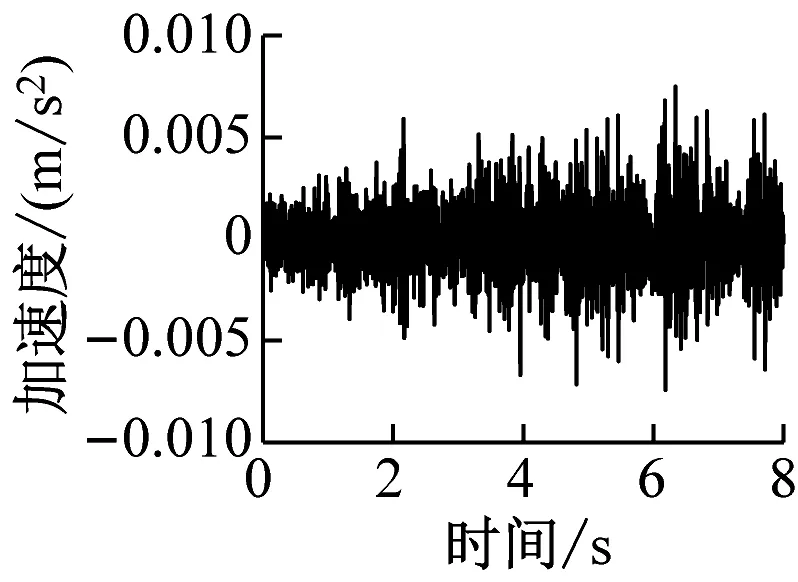
e) B16

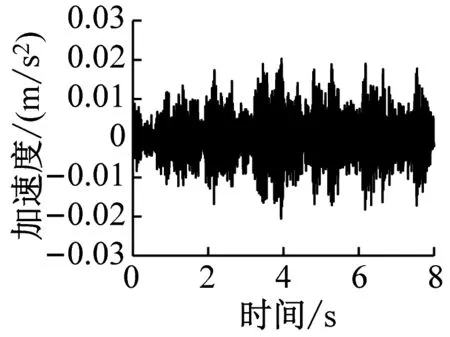
a) C1

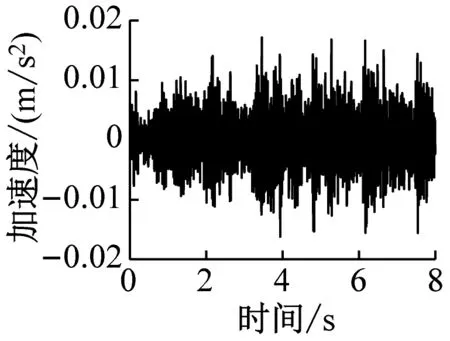
b) C4

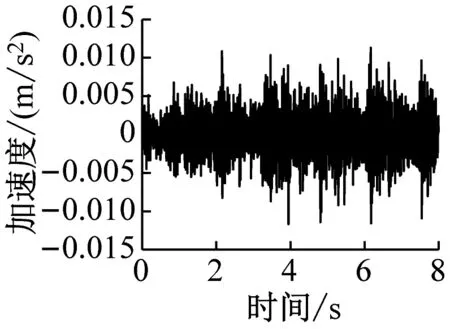
c) C7

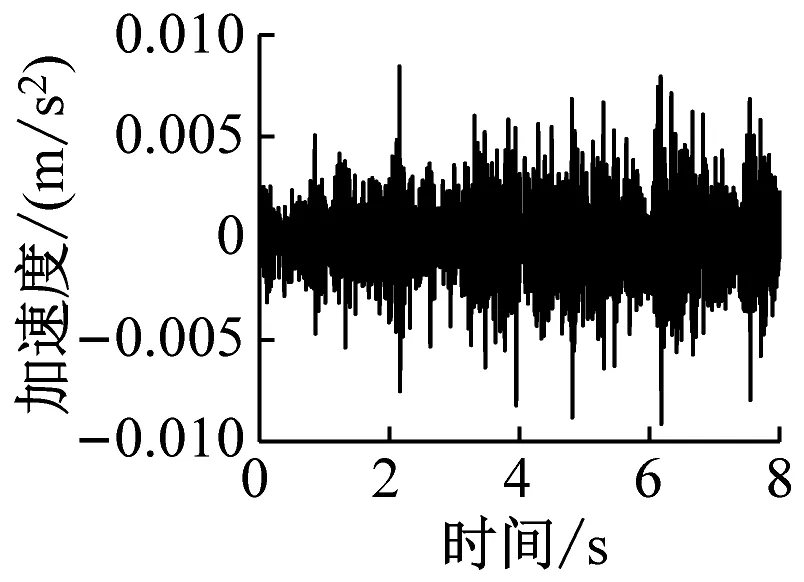
d) C13

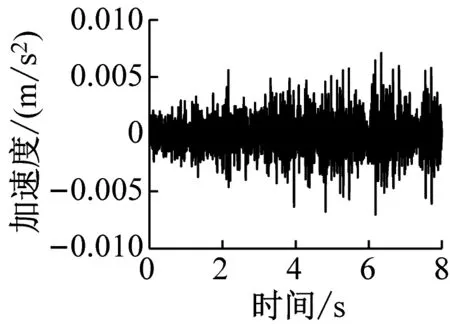
e) C16

由图4～图6得，当列车穿过建筑物时，楼层越低，房间地板加速度越大，同一楼层不同房间的加速度幅值差异不大。

3.2 Z振级计算结果

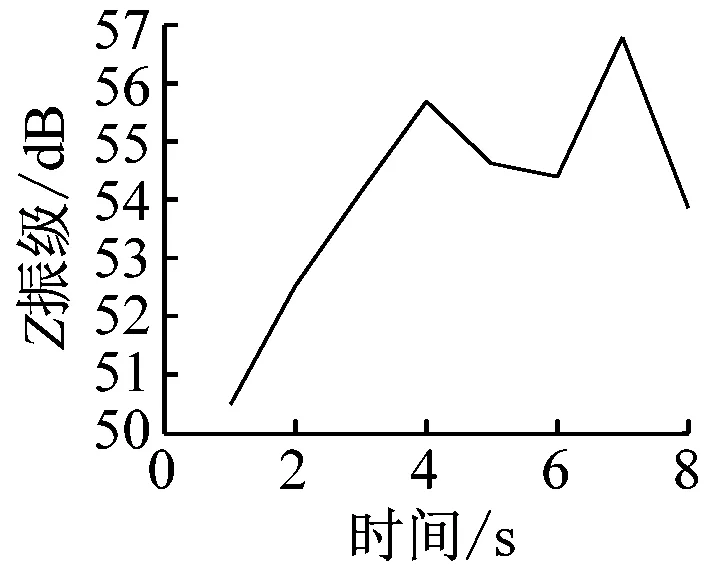
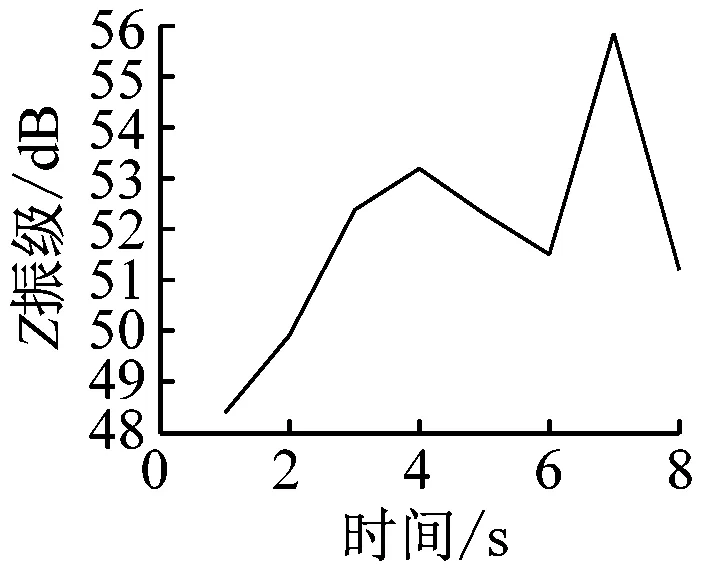
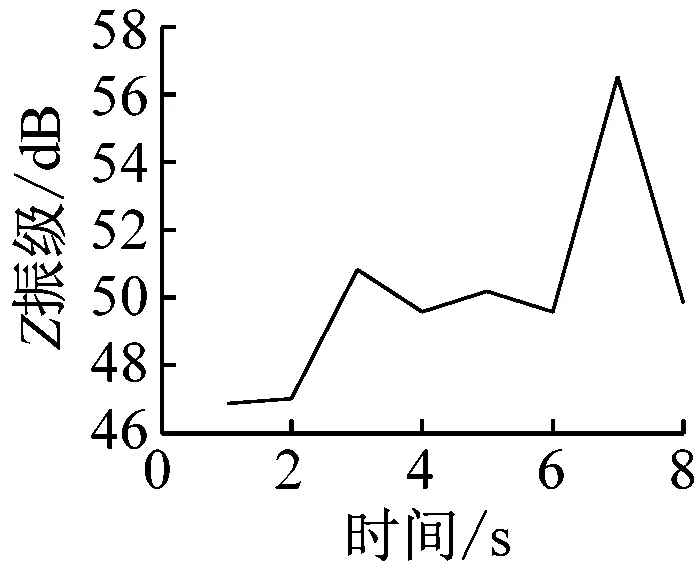
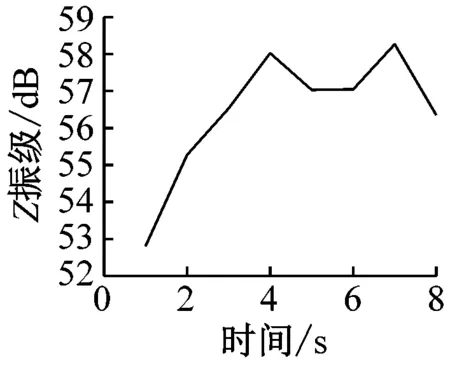
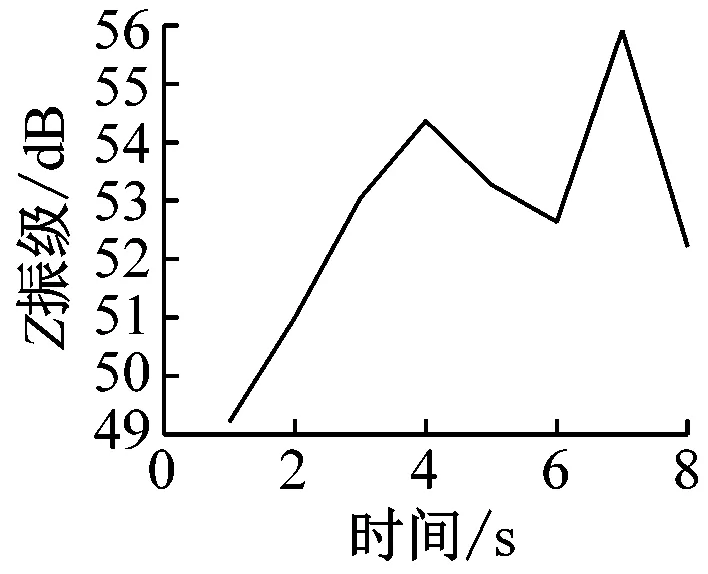
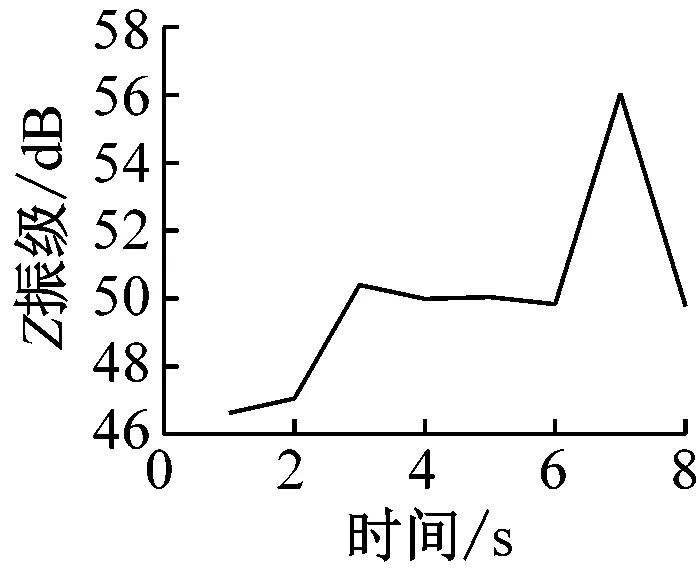
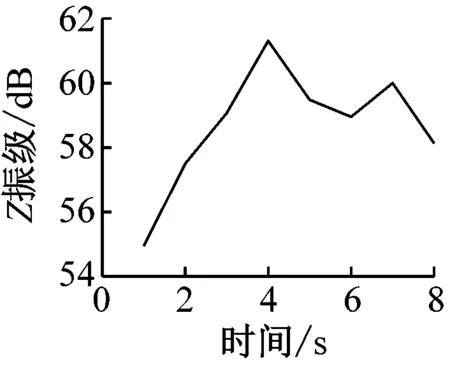
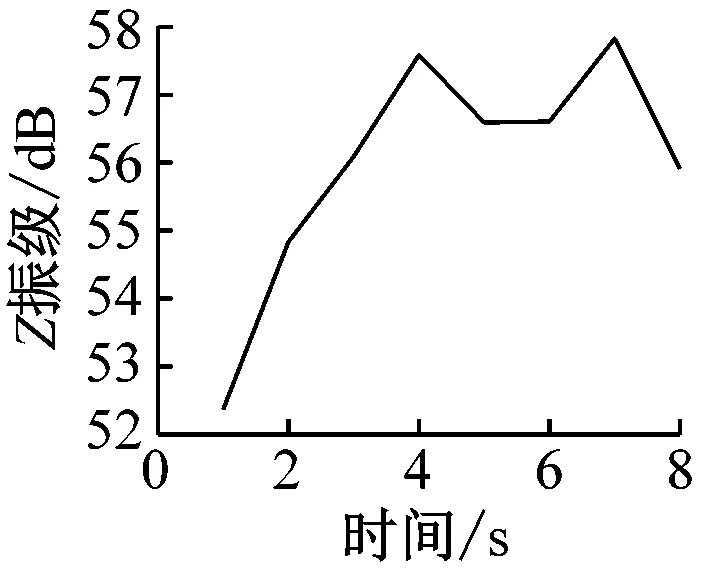
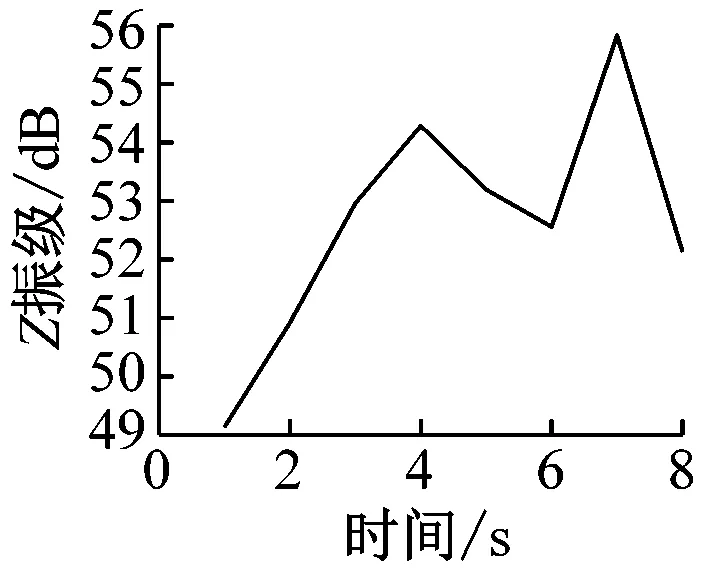
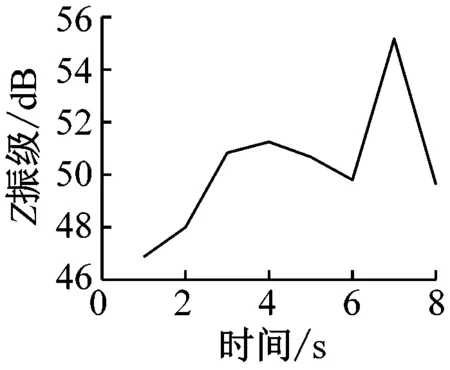
在获得室内楼板的加速度时程曲线后，分析每秒内各观测点处的振动加速度Z振级最大值，各观测点Z振级最值随时间变化的曲线如图7所示。

通过分析可以发现，室内振动需要一定时间的激励才能达到峰值。1楼的振动峰值出现在振动开始4 s后，而4楼、7楼、13楼和16楼的振动峰值均出现在振动开始约7 s后。楼层越低，达到振动峰值所需的激励时间越短。

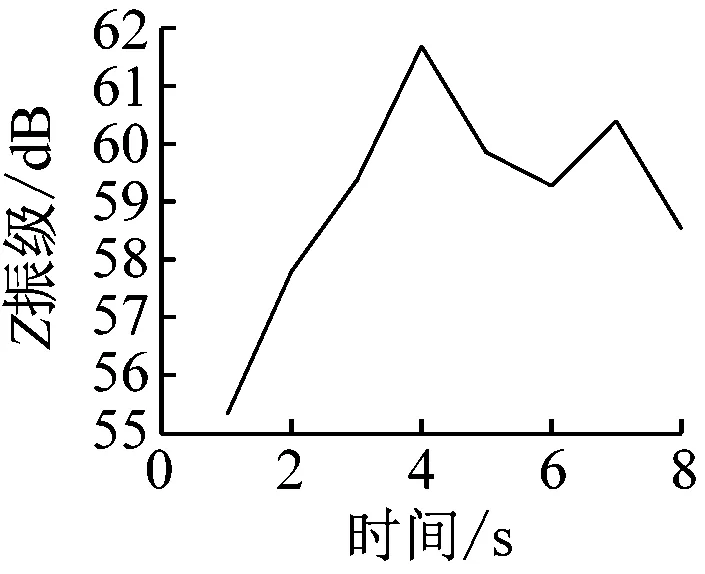
a) A1

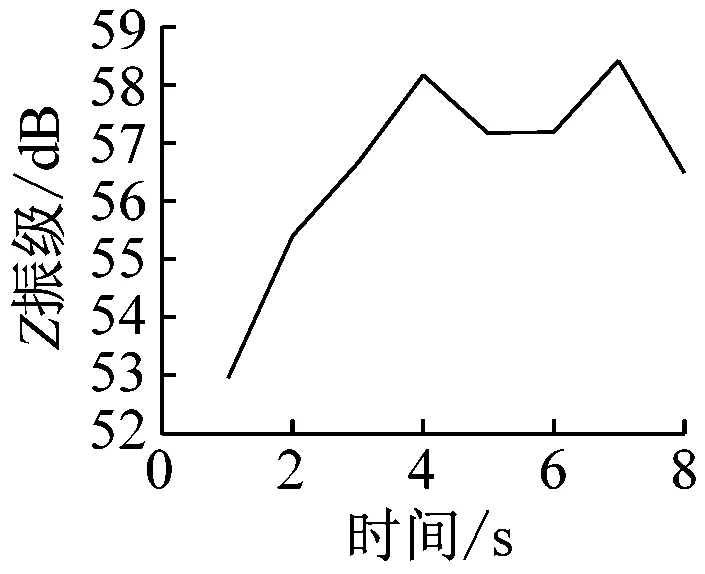
b) A4

c) A7

d) A13

e) A16

a) B1

b) B4

c) B7

d) B13

e) B16

a) C1

b) C4

c) C7

d) C13

e) C16

最后容易得到计算时间内列车下穿的某建筑物时室内各观测点的Z振级最大值，如表6所示。

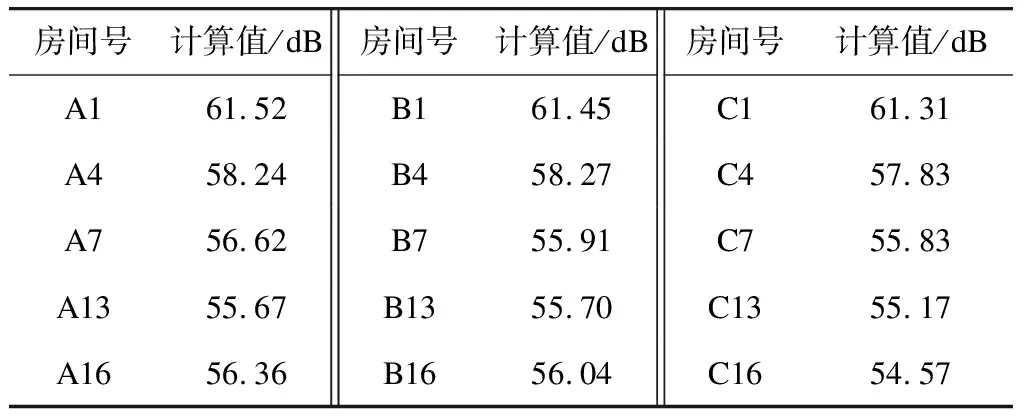
表6 某建筑物部分楼层地板Z振级最大值

由表6可知：在同一观测断面中，随着楼层增加，Z振级均逐渐减小，振级最大值都出现在一楼；同一楼层中，室内振动最小值均发生在离外墙最远的区域，楼层较低时，同一楼层不同区域的振动噪声差异不大，楼层越高，位置分布对于同楼层间的振动影响越显著。最终得出使用有限元法预测的该建筑物室内振动为61.5 dB。

4 两种方法对比分析

经验法的优点是计算过程更为简便，且能方便地考虑车速、车辆、钢轨、线路形状、建筑物类型、建筑物与线路位置关系等因素，能够快速全面地得到不同建筑物的室内振动最大值；缺点是考虑修正项时较为粗糙，存在一定误差，且无法分析振动具体的传播规律。有限元法的优点是能细致考虑线路、土层、建筑物的特性，常用于需要对振动及其传播规律进行细致分析的情况；缺点是建模和计算耗时耗力，计算成本较高。

根据以往实测经验和研究成果，本文以城市轨道下穿建筑物时预测出的室内最大振动作为该地块上所有建筑物的室内振动最大值，得出数值仿真法下该地块上建筑物室内最大振级预测值为61.5 dB，与使用经验法得出的59～63 dB区间相符，且两种方法的预测结果均满足《城市区域环境振动标准》[8]中居民和文教区昼间70 dB、夜间67 dB的限值要求。

5 结论

1) 相同水平高度条件下，建筑物离城市轨道线路的水平距离越近，受列车运行的振动影响越大，当线路下穿建筑物时，该楼的室内振动最大。

2) 当建筑物与线路的水平距离超过52 m时，建筑物室内振动预测值将低于50 dB，由于该部分振动在现场测试时采集数据将难以探测，建议实际测试时根据建筑物与线路的水平距离合理选择测试对象。

3) 室内振动需要一定时间的激励才能达到峰值，楼层越低，达到振动峰值所需的激励时间越短。

4) 室内振动随着楼层增加逐渐减小，同一建筑物中振级最大值出现在楼层最低的一楼。

5) 同一楼层中，室内振动最小值均发生在离外墙最远的区域，楼层较低时，同一楼层不同区域的振动噪声差异不大，楼层越高，位置对于同楼层间的振动影响越显著。

6) 经验法与有限元法两种方法预测结果符合度较高，两种方法各有优劣，需要根据不同情况选择适用的预测方法。经验法具有计算简便的优点，适用于一般工程中需要知道最大室内振动是否超限的情况；有限元法考虑因素更为全面和细致，但是计算成本较高，适用于需要考虑楼层和房间位置的情况。