基于无监督深度学习的多波AVO反演及储层流体识别
2021-06-01孙宇航陈天胜
孙宇航,刘 洋,3,陈天胜
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京102249;2.中国石油大学(北京)CNPC物探重点实验室,北京102249;3.中国石油大学(北京)克拉玛依校区,新疆克拉玛依834000;4.中国石油化工股份有限公司石油勘探开发研究院,北京100083)
储层流体识别是地震勘探中的重要环节,主要通过地震波的速度、地下介质的密度和流体因子等参数识别地下的储层岩性和流体等。流体因子是由地震波速度和地下介质密度组合得到的能够反映储层特征的参数,在储层流体识别中发挥着重要的作用。流体因子的发展先后经历了加权差类[1-2]、拉梅常数类[3-4]、模量类[5-6]、Gassmann流体项[7-8]和等效流体体积模量[9-10]等阶段。等效流体体积模量以其对储层流体的高敏感性成为现阶段的研究热点。
地震反演是从地震数据中提取流体因子的有效手段,分为叠前反演和叠后反演。相对于后者,叠前反演利用包含更多储层信息的叠前道集数据,反演结果的分辨率更高。AVO反演是最为常用的叠前反演方法之一。常规AVO反演方法大多只利用纵波道集,只考虑了纵波对流体的敏感性,忽视了横波对岩性的敏感性。同时利用纵波和转换波道集进行AVO反演能够弥补纵波AVO反演的不足,提高反演的精度和稳定性[11-12]。传统的多波AVO反演大多基于最小二乘或贝叶斯理论构建反演的目标函数[13-15],取得了较好的应用效果。但这种方法的反演精度高度依赖于初始模型的精度,目前大多数实际工区很难建立高精度的初始模型。近年来,受益于计算机计算能力的提升,深度学习方法迅速发展并被应用于叠后波阻抗反演和叠前AVO反演[16-19],取得了较好的结果。深度学习分为有监督和无监督两种。相对于前者,无监督深度学习方法不需要制作大量高精度的样本数据,具有更高的实用价值。
目前已有的流体因子反演方法可以分为直接法和间接法。前者直接基于地震记录反演得到流体因子,后者先基于地震记录反演得到速度和密度,然后组合得到流体因子。相对而言,直接法不需要进行组合计算,避免了反演过程中产生的累计误差,反演结果的精度更高。此外,在叠前反演中,密度的反演结果精度较低,利用间接法反演得到的密度会影响组合流体因子的精度。
为了提高储层流体识别的精度,基于AVO和深度学习理论,本文提出了一种利用纵波和转换波道集直接反演流体因子的无监督方法。本文主要研究针对砂岩储层的流体识别。首先,利用砂岩储层的模型和实际数据分析了各种流体因子对储层流体的敏感性;然后,基于叠前AVO理论的指导构建了一种多波直接反演流体因子的无监督深度学习方法;最后,将该方法应用于X工区的实际数据反演等效流体体积模量并进行储层流体识别,从而证明了该方法的反演精度和适用性。
1 砂岩储层流体因子分析
1.1 基于模型数据分析流体因子的敏感性
利用典型砂岩模型[20]分析不同流体因子对储层流体的敏感性。砂岩模型参数如表1所示。利用表中数据分别计算泊松比、拉梅常数、纵波模量、Russell流体因子和等效流体体积模量,对计算结果进行归一化处理并对比,结果如图1所示,其中,红色和蓝色的面积差异越大,代表流体因子对储层流体的敏感性越好。由图1可见,在两类砂岩模型中,Russell流体因子和等效流体体积模量所在的矩形中红色和蓝色的面积差异较大,其中等效流体体积模量对应的面积差异最大,证明等效流体体积模量对储层流体具有相对更高的敏感性。

表1 典型砂岩模型参数
1.2 基于实际数据分析流体因子的敏感性
利用X工区实际测井数据分析流体因子对储层流体的敏感性。考虑到利用模型数据分析时,纵波模量、Russell流体因子和等效流体体积模量对储层流体的敏感性较高,基于测井数据只计算这3种流体因子。结合已知测井解释结果,分别做流体因子和孔隙度的交会分析,结果如图2所示,由图2可知,纵波模量和Russell流体因子并不能较好地区分含气砂岩和含水砂岩,等效流体体积模量能够区分这两种砂岩,含气砂岩的取值范围为-0.7~0.3GPa,含水砂岩的取值范围为-1.0~0.7GPa。
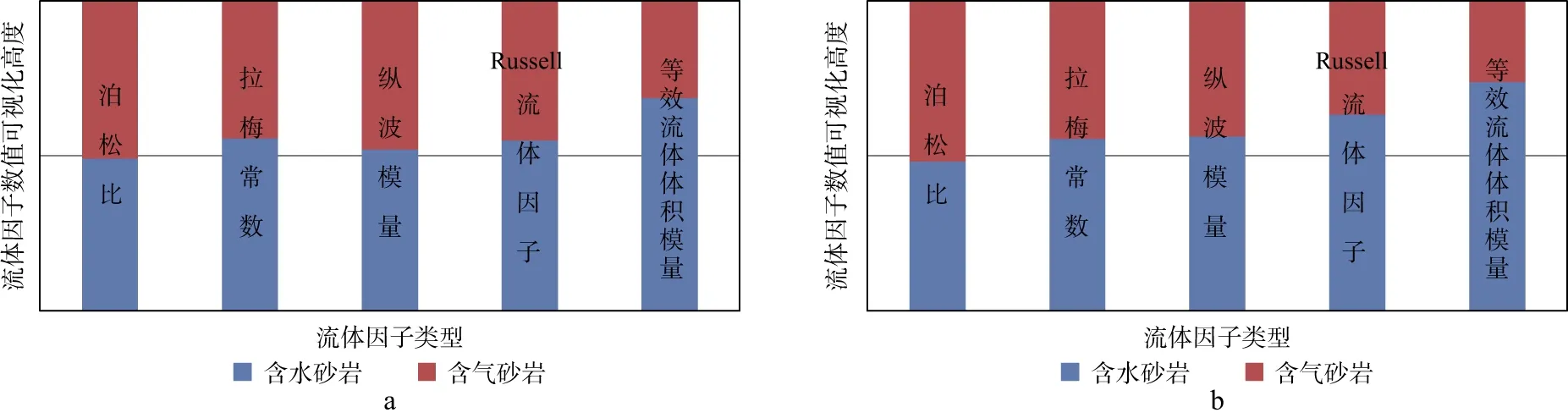
图1 典型砂岩模型中不同流体因子对比结果a 第一类砂岩模型; b 第二类砂岩模型
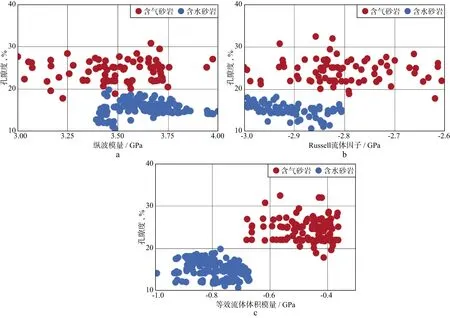
图2 不同流体因子与孔隙度的交会分析a 纵波模量; b Russell流体因子; c 等效流体体积模量
综合模型数据和实际数据的分析结果认为,等效流体体积模量对砂岩储层流体的敏感性更好,本文提出的流体因子反演方法主要针对砂岩储层进行等效流体体积模量反演。
2 基于无监督深度学习的多波AVO反演方法
2.1 多波AVO反演理论
叠前AVO反演基于褶积模型理论,若不考虑地震子波对地震频带的影响,并假设噪声水平为0,地震褶积模型可以表示为:
d=W*R
(1)
式中:d为地震记录;W为子波褶积矩阵;R代表反射系数。R可以表示为:
R=Gm
(2)
式中:m表示地层参数组成的矩阵;G表示R与m之间的映射矩阵。一般利用Zoeppritz方程来表示地层参数与反射系数之间的关系,其表达式为:
(3)
式中:θ1和θ2分别代表纵波的反射角和透射角;θ3和θ4分别代表转换波的反射角和透射角;α、β和ρ分别代表纵波速度、横波速度和密度;下标1和2分别代表上层和下层介质;R和T分别代表反射系数和透射系数;下标PP和PS分别代表纵波和转换波。
为了能够直接反演等效流体体积模量,将公式(3)改写为由等效流体体积模量直接表示反射系数的矩阵方程。其本质是实现速度与等效流体体积模量之间的相互转化。目前还没有直接表示两者之间关系的表达式,这里引入第3个参数Gassman流体项,Gassmann流体项与速度之间的关系式[7]为:

(4)
式中:f代表Gassmann流体项;γd代表干岩石中的纵、横波速度比;μ代表剪切模量。
Gassmann流体项还可以表示[21]为:
f=GKf
(5)
其中,
(6)
式中:Kf代表等效流体体积模量;Kdry和Ks分别代表干岩石和岩石骨架的体积模量;φ代表孔隙度。
结合临界孔隙度模型,公式(6)中干岩石的体积模量可以表示为:
(7)
式中:φc代表临界孔隙度。
将公式(5),(6)和(7)代入公式(4)可以得到纵波速度与等效流体体积模量之间的关系式,即:
(8)
将公式(8)代入公式(3),可以得到直接利用等效流体体积模量表示反射系数的矩阵方程,其中,界面上层的纵波速度α1由界面上层的等效流体体积模量Kf1、孔隙度φ1、密度ρ1和横波速度β1计算得到;界面下层的纵波速度α2由界面下层的等效流体体积模量Kf2、孔隙度φ2、密度ρ2和横波速度β2计算得到。
结合公式(1)和公式(2),地震记录可以表示为:
d=W*Gm
(9)
常规AVO反演的流程如图2所示。首先,给出初始模型m初;然后,根据公式(9)计算合成地震记录d合;接着,计算实际地震记录d实与合成地震记录d合的L2范数:
L2=‖(d实-d合)‖2
(10)
判断L2范数是否满足设定的迭代终止条件,若满足则此时的m初就是反演结果,若不满足则更新m初直到L2范数满足迭代终止条件。传统的AVO反演方法一般基于最小二乘或贝叶斯理论更新m初,本文基于深度学习更新m初。此外,本文提出的反演方法利用多波叠前道集,目标函数的表达式为:
L2=‖η(dPP实-dPP合)2+(1-η)(dPS实-dPS合)‖2
(11)
式中:η为加权因子,由纵波和转换波资料的品质决定各自在反演中占的比重。

图3 常规AVO反演流程
2.2 深度学习理论
随着计算能力的提高,深度学习因其解决问题的泛化能力被广泛应用于各行各业。深度学习以神经网络结构为基础。神经网络结构分为全连接神经网络(full connected,FC)、卷积神经网络(convolutional neural networks,CNN)和循环神经网络(recurrent neural network,RNN),不同的神经网络具有不同的特点,适合处理不同的问题。全连接神经网络是所有网络的基本结构;卷积神经网络具有强大的空间特征提取与信息整合能力,适合处理视觉领域的图像识别分类问题;循环神经网络具有动态特征和记忆功能,适合处理涉及时序数列的问题。AVO反演中涉及的数据均是连续的,属于时序数列。因此,基于循环神经网络构建AVO反演方法具有更大的优势。循环神经网络具有一种重复神经网络模块的链式结构(图4),包括输入层、隐藏层和输出层。图4中,xt表示t时刻的输入,ht表示t时刻的输出。隐藏层中包含了重复的神经网络模块。常规循环神经网络能够有效地分析和处理较短的时序数列,但不能分析和处理维度过长的时序数列,否则会产生“梯度消失”或“梯度爆炸”的问题。循环神经网络中的一种改进结构长短时记忆神经网络(long short term memory network,LSTM)通过“门”的结构(遗忘门、输入门和输出门)实现信息的添加或删除,改善了常规循环神经网络不能处理较长时序数列的问题。但是,长短时记忆神经网络的重复结构过于复杂,样本训练需要花费大量的时间,因此长短时记忆神经网络存在很多变体,门控循环神经网络(gated recurrent unit,GRU)是最为成功的变体之一。门控循环神经网络利用重置门和更新门代替了长短时记忆神经网络中的遗忘门、输入门和输出门(图5)。图5中,xt,ht,rt,zt和mt分别表示t时刻的输入、输出、更新门的值、重置门的值和候选值,sig和tanh分别代表sigmoid函数和tanh函数。实验证明,门控循环神经网络和长短时记忆神经网络的识别精度相当,但门控循环神经网络更易于训练,效率更高[22]。
对于GRU神经网络的隐藏层,给定输入值xt(t=1,2,…,n),t时刻隐藏层的值为:
zt=sig(Wz·[ht-1,xt])
(12a)
rt=sig(Wr·[ht-1,xt])
(12b)
mt=tanh(Wm·[rt·ht-1,xt])
(12c)
ht=(1-zt)ºht-1+ztºmt
(12d)
式中:ht代表t时刻输出层的值;ht-1代表t-1时刻输出层的值;zt代表t时刻更新门的值;rt代表t时刻重置门的值;mt代表t时刻的候选值;W代表权重矩阵;[]表示两个向量相连接;·是一种矩阵间的计算方法,表示按元素乘。tanh函数表达式为:
(13a)
tanh函数的取值范围为(-1,1)。sigmoid函数表达式为:
(13b)
sigmoid函数的取值范围为(0,1)。

图4 循环神经网络中的重复链式结构示意

图5 门控循环神经网络中链式结构示意
GRU神经网络需要训练的权重矩阵为Wz,Wr和Wm,它们分别由两个权重矩阵组合而成,即:
Wz=Wzx+Wzm
(14a)
Wr=Wrx+Wrm
(14b)
Wm=Wmx+Wmm
(14c)
式中:Wzx,Wrx和Wmx分别为输入值到更新门的权重矩阵、输入值到重置门的权重矩阵和输入值到候选值的权重矩阵;Wzm,Wrm和Wmm分别为上一次的候选值到更新门的权重矩阵、上一次的候选值到重置门的权重矩阵和上一次的候选值到候选值的权重矩阵。
2.3 基于无监督深度学习的多波AVO反演方法
结合AVO反演理论和门控循环神经网络,本文提出了一种基于无监督深度学习的多波AVO反演方法,直接反演等效流体体积模量,其技术流程如图6 所示。图6中,红框内为神经网络结构,包含1个输入层、n个GRU隐藏层和1个输出层。

图6 基于无监督深度学习的多波AVO反演方法流程
首先,对纵波和转换波叠前道集进行归一化处理,归一化公式为:
(15)
式中:xmin和xmax为xi的最小值和最大值。
然后,将归一化的叠前道集和初始的权重矩阵输入到神经网络结构中,输出初始的等效流体体积模量、横波速度和密度,接着利用推导得到矩阵方程,基于神经网络输出的初始参数,分别计算纵波和转换波反射系数,并与地震子波褶积合成叠前道集。
最后,利用公式(11)计算实际和合成道集的L2范数,判断其是否满足迭代终止条件,若满足,则输出此时的等效流体体积模量,若不满足,则更新神经网络结构中的权重矩阵。其中,叠前道集的合成涉及到反射系数的计算,本文用公式(3)和公式(8)计算反射系数并约束神经网络的训练,实现等效流体体积模量的确定性反演。采用基于反向传播理论的训练方法更新权重系数,其中,利用随机梯度下降法(stochastic gradient descent,SGD)计算权重梯度。在AVO理论的指导下,该方法不需要制作训练样本就能实现等效流体体积模量的预测,是一种典型的无监督深度学习方法。此外,为了提高反演结果的横向连续性,在输入叠前道集之前做叠加处理,将相邻5道或9道的叠前道集叠加为中心道(图7)。
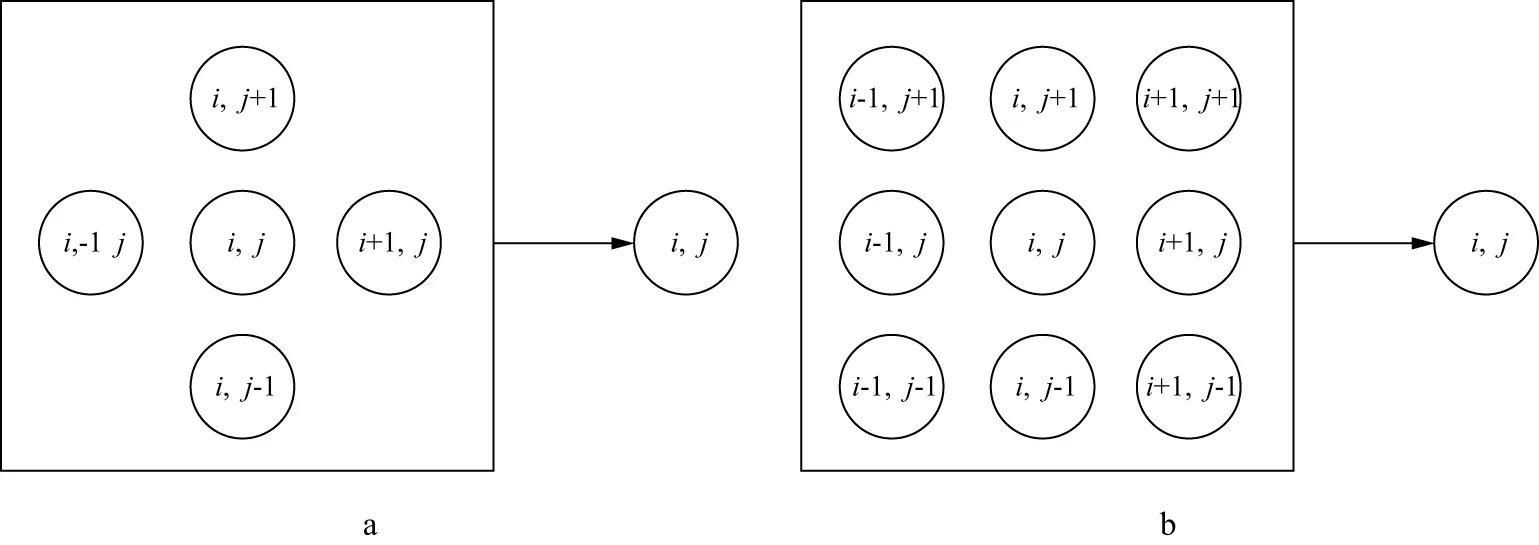
图7 输入道集之前的叠加处理示意a 5道叠加; b 9道叠加
3 实际工区储层流体识别试算
将上述方法应用于X工区,基于纵波和转换波叠前道集直接反演等效流体体积模量并进行储层流体识别。
3.1 实际工区介绍
X工区位于我国北部,烃源岩厚度分布不均,单砂体薄,气水识别不清。工区底图如图8所示,包含301条Inline和301条Xline,有纵波和转换波叠前道集,采样间隔为4ms,偏移距范围为75~4275m,间隔为150m。目的层埋深约3000~3170m,转换到时间域约为1600~1700ms。共有4口测井(A1、A2、A3和A4),每口测井数据中包含纵波速度、横波速度、密度、孔隙度和含气饱和度。根据已知测井解释结果,在1620ms处,4口测井均处于气藏有利区带。
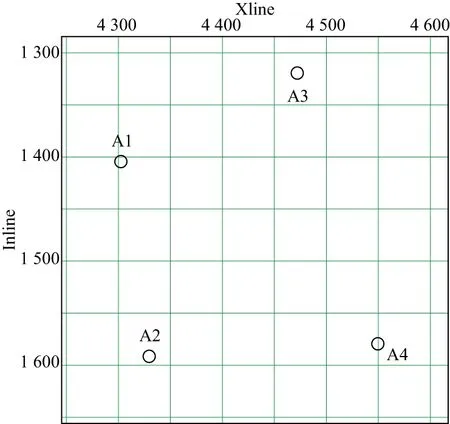
图8 X工区底图
3.2 流体因子直接反演及储层流体识别
在进行等效流体体积模量直接反演之前,需要对数据进行预处理。首先,对道集进行频谱分析,确定主频和有效频带并进行带通滤波;然后,进行噪声压制以提高信噪比,包括面波、线性干扰和随机干扰的压制;最后,在保证足够信噪比的前提下,再对地震道集进行反褶积以提高分辨率,包括地表一致性反褶积和预测反褶积。将处理好的叠前道集进行归一化,使其值域处于(0,1),便于在神经网络结构中的计算;对测井数据进行异常值处理,作为评价反演结果的比对数据。然后进行井震标定,并将纵波和转换波叠前道集进行偏移距叠加,分别将偏移距75~1325m,1075~2325m,2075~3325m和3075~4275m叠加为偏移距700m,1700,2700和3675m,图9为过井A1和A2的纵波和转换波分偏移距道集叠加剖面。考虑到目的层的埋深,将反演的时窗确定为1550~1750ms。AVO反演基于褶积模型,地震子波的提取对于反演结果具有很大的影响。地震子波的提取方法主要分为确定性和统计性提取方法,前者利用测井资料和井旁地震道求取地震子波,依赖于测井资料,得到的子波较为复杂。统计性子波提取方法主要通过地震道自身估计地震子波,与地震数据的相关性更好。利用X工区的地震道集提取统计子波并构建子波矩阵,将偏移距叠加后的叠前道集分别经过图7b 所示的9道叠加后输入到构建好的神经网络结构中,进行训练和反演。每次输入一道的偏移距分别为700,1700,2700和3675m的纵波和转换波道集,输出一道的等效流体体积模量。经过多次测试,本次反演涉及的神经网络结构包含1个输入层、5个GRU隐藏层和1个输出层,每个GRU隐藏层包括32个神经元,学习步长为0.02。综合考虑纵波和转换波道集的品质,通过4口测井井旁道叠前道集的试算,将目标函数中的加权因子η赋值为0.7。

图9 过井A1和A2的不同分偏移距道集叠加剖面a 纵波剖面; b 转换波剖面
分别用基于无监督深度学习的多波直接反演、纵波直接反演和多波间接反演方法对工区内4口测井的井旁道地震道集进行等效流体体积模量反演。在运算时间相同的情况下,3种方法对应的反演结果与测井数据曲线如图10所示。由图10可知,在4口测井中,反演结果与测井数据的曲线趋于一致。本文利用相对误差衡量反演结果的精度,相对误差越小代表反演精度越高。3种方法对应的反演结果与测井数据的相对误差如表2所示。由表2可知,基于无监督深度学习的多波直接反演方法对应的结果与测井数据之间的相对误差最小,平均为2.949%;纵波直接反演方法对应的结果与测井数据之间的相对误差最大,平均为5.369%。图11展示了反演结果与测井数据之间的绝对误差,由图11可知,4口测井的反演结果与测井数据的绝对误差在0.3GPa内,具有较好的匹配度;多波直接反演对应的绝对误差最小,在0.1GPa之内,纵波直接反演对应的绝对误差最大。为了评价反演方法的稳定性,我们将公式(11)的最小化定义为神经网络的损失函数。图12展示了多波直接方法在反演过程中的损失函数变化。由图12可知,在迭代20次左右后,4口测井的损失函数值均接近于0并趋于稳定。综上所述,基于无监督深度学习的多波直接反演方法具有较高的反演精度和稳定性。

图10 3种方法的反演结果与测井数据对比

表2 不同方法对应的反演结果与测井数据的相对误差 %
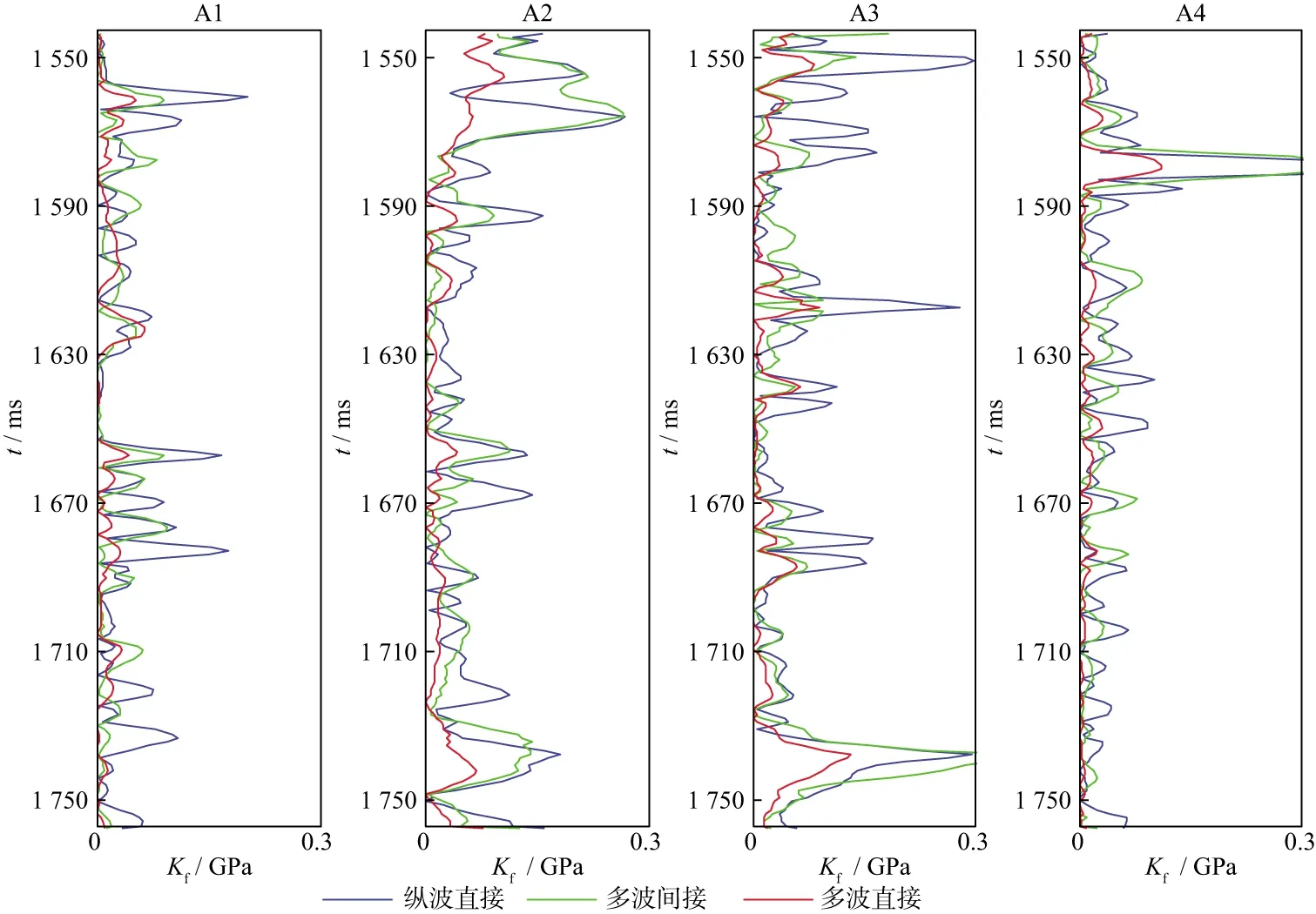
图11 不同方法的反演结果与测井数据的绝对误差对比
将多波直接反演方法应用于整个X工区进行等效流体体积模量反演,过井A1和A2的剖面如图13a 所示,过井A3和A4的剖面如图13b所示,其中,测井曲线显示的是含气饱和度,含气饱和度较大的区域代表气层有利区。剖面中红色、黄色和其它颜色分别代表含气砂岩、含水砂岩和其它砂岩。由图13可知,反演剖面连续性良好且与测井曲线吻合度良好。抽取1620ms的时间切片如图14所示,其中红色的值域为-0.7~ 0GPa,代表含气砂岩。由图14可知,1620ms处,4口测井均处于含气砂岩储层,与已知测井解释结果吻合,验证了该方法的有效性。

图12 多波直接方法反演过程中的损失函数变化

图13 等效流体体积模量剖面a 过井A1和A2的等效流体体积模量剖面; b 过井A3和A4的等效流体体积模量剖面
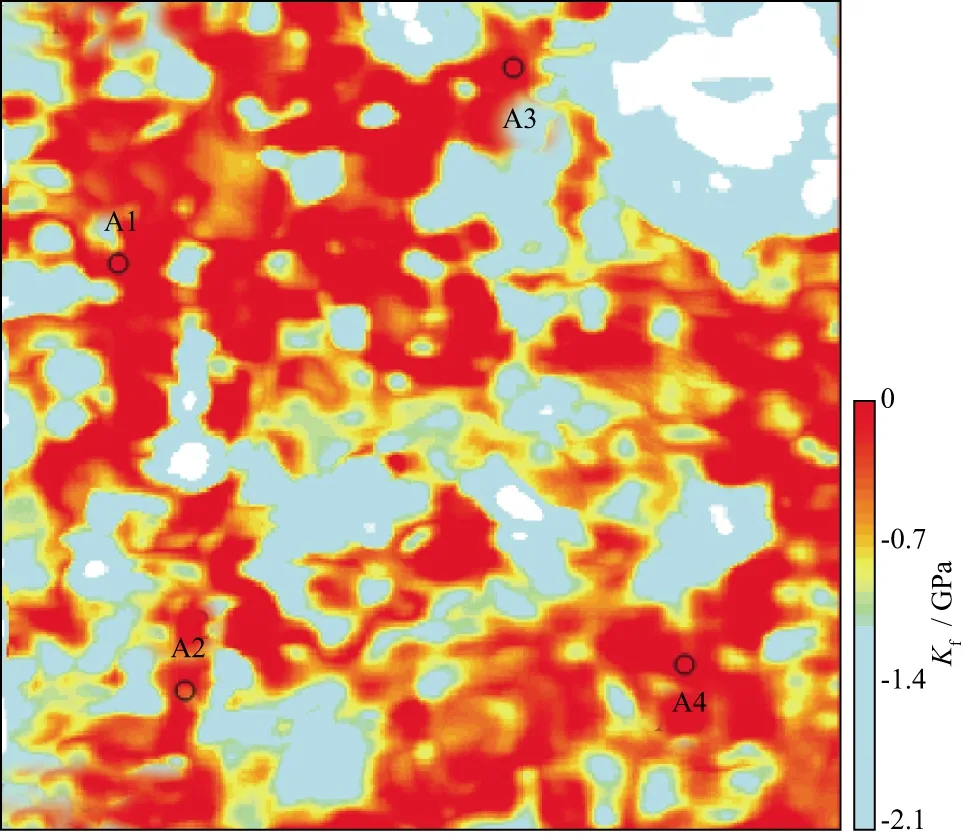
图14 1620ms等效流体体积模量时间切片
4 结论与认识
本文基于AVO理论和深度学习方法,提出了一种基于无监督深度学习的多波AVO反演方法,直接反演等效流体体积模量。将该方法应用于X工区的实际数据反演以及储层流体识别,得到以下结论:
1) 对于砂岩储层,等效流体体积模量对储层流体的敏感性相对较好,能够区分含气砂岩和含水砂岩;
2) 基于无监督深度学习的多波直接反演方法比纵波直接反演和多波间接反演方法的精度更高,多波直接反演的结果与测井数据的相对误差约为2.949%,绝对误差小于0.1GPa;
3) 利用基于无监督深度学习的多波AVO直接反演方法反演得到的等效流体体积模量能够较为精准地识别储层流体。
