南疆丰收灌区水资源多目标优化配置方案优选

何 英，唐晓宇，彭 亮，居金浩

南疆丰收灌区水资源多目标优化配置方案优选

何 英，唐晓宇，彭 亮，居金浩

（1. 新疆农业大学水利与土木工程学院，乌鲁木齐 830052；2. 新疆水利工程安全与水灾害防治重点实验室，乌鲁木齐 830052）

针对灌区水资源多目标优化配置模型求解算法的不确定性和最优方案选择问题，以新疆阿克苏地区阿瓦提县丰收灌区为研究对象，以灌区可持续发展为目标，建立基于优选算法的灌区水资源多目标优化配置及方案优选模型。对比改进的NSGA-II算法（Non-dominated Sorting Genetic Algorithm-II，带精英策略的非支配排序遗传算法）、NSGA-III算法（Non-dominated Sorting Genetic Algorithm-III，基于参考点的非支配排序遗传算法）、MOEA/D算法（A Multi-Objective Evolutionary Algorithm based on Decomposition，基于分解的多目标进化算法），最终选取性能最好的CNSGA-III算法作为优化算法对水资源配置模型进行求解；建立水资源配置方案评价体系，利用熵权-TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution，优劣解距离法）综合评价模型对符合决策制定者期望的配置方案进行对比筛选，选出灌区水资源最佳配置方案。结果表明：优化后的方案相较于传统配置方案，在“三条红线”用水限额下，经济净效益增加1.0%，灌区总缺水量减少8.4%，碳吸收总量增加4.5%。建立的灌区水资源多目标优化配置及方案优选模型可为管理者制定灌区水资源配置方案提供参考，也可适用于其他干旱灌区，有一定的理论意义。

水资源；算法；多目标；不确定性；评价模型；灌区

0 引 言

丰收灌区作为优质的棉花生产基地，被赞为“中国长绒棉之乡”。近年来，由于灌区管理者盲目追求经济效益，大开荒地，侵占生态用地，加之上游阿克苏河来水量减少、为保证塔里木河输水目标而实施的灌区引水量减少等措施，导致灌区水资源极度短缺且配置不合理，生态环境越发脆弱，阻碍灌区的可持续发展[1-3]。因此，对灌区内有限的水资源进行优化配置是当前亟待解决的问题。

灌区水资源优化配置通过调整作物种植面积、优化种植结构，来实现灌溉水资源高效利用，对协调区域作物生产和生态环境保护产生积极影响[4]。农业水资源管理需要权衡多方利益，涉及经济、社会和生态环境等方面[5-6]。近年来，针对灌区水资源优化配置问题，学者们提出了不同的优化配置方法。陈卫宾等[7]提出基于记忆梯度混合遗传算法，用于解决灌区水资源优化配置模型中目标函数高度非线性的问题。Zhang等[8]以灌溉净效益最大为目标，建立了农业水资源优化配置模型。张展羽等[9]将多阶段人工鱼群算法用于求解缺水灌区的农业水土资源优化配置模型中。陈述等[10]利用粒子群人工蜂群混合算法对渠-塘优化调控与田间多种作物优化配水相结合的耦合模型求解。以上研究都只考虑单一目标函数，属于单目标优化模型，而灌区水资源配置往往受到经济效益、社会效益和生态效益等多因素的影响。为解决多因素影响问题，灌区水资源多目标优化配置模型相继被提出。郭萍等[11]建立非线性多目标水土资源联合配置模型，并采用遗传算法对其求解。Anwar等[12]以灌区单月作物产量最高以及农民总体收益最大为优化目标，并采用多目标遗传算法（Multi-Objective Genetic Algorithm, MOGA）对模型进行了求解。岳琼等[13]以农业灌溉净经济效益最大和绿水利用占比最大为目标，建立了模糊可信性随机多目标农业水资源优化配置模型。Chen等[14]采用协同理论建立水-能源-粮食系统框架，并用遗传算法对其进行评估。上述传统水资源配置研究仅采用单一方法对目标规划模型求解，没有考虑对求解方法进行比较，且没有对配置方案进行优选，可能导致配置方案的配水效果略差。

基于此，本文以灌区可持续发展为目标，建立基于优选算法的灌区水资源多目标优化配置及方案优选模型（Multi-Objective Optimal Allocation Model of Water Resources in Irrigation Area Based on Algorithm Selection and Plan Optimization，MOASPO），该模型可依据不同算法对多目标优化模型求解性能的差异选取性能较好的算法；然后结合当地实际情况建立灌区水资源配置方案评价体系，利用熵权-TOPSIS综合评价模型对满足决策制定者期望的非劣解进行筛选，选择灌区水资源最佳配置方案。将建立的MOASPO模型应用于水资源短缺的丰收灌区，得到灌区水资源配置方案，可为当地管理者提供理论依据和决策参考。

1 材料与方法

1.1 研究区概况

丰收灌区位于新疆阿克苏地区阿瓦提县的西南部（40°20′～40°38′N，80°10′～80°20′E），处于亚欧大陆腹地的塔里木盆地西北边缘。该地区属暖温带大陆性荒漠气候，夏季炎热，冬季寒冷，昼夜温差较大，光照充足，降水稀少，蒸发强烈。年平均气温10.5 ℃，7月份气温最高，1月份最低。年平均降水量47.8 mm，主要集中在6—8月，约占全年降水量的60%。年蒸发量1 905.2 mm，远大于降水量，灌区农业生产主要依靠灌溉。丰收灌区是全国著名的优质棉花生产基地，被誉为“中国长绒棉之乡”。区内主要农作物为棉花、玉米和冬小麦，其中棉花为经济作物，玉米和冬小麦为粮食作物。

1.2 模型介绍

MOASPO模型用于解决灌区水资源配置模型求解算法的不确定性和最优方案选择问题，由水资源优化配置和配置方案优选2个模块组成。模型结构如图1所示。

1.3 水资源多目标优化配置模型

1.3.1 目标函数

灌区可持续发展是灌区水资源配置的前提，本研究以灌区经济净效益最大、总缺水量最小和碳吸收总量最大为目标函数。

1）经济净效益

灌区经济净效益是衡量灌区人民生活质量的重要标准，由灌区作物的种植面积和产量决定，而灌区水资源的合理配置是影响作物产量的主要因素。为使灌区的经济净效益达到最大，在非充分灌溉条件下，通过调整各作物的种植结构和优化其灌溉制度，使灌区的土地资源和水资源得到充分利用，优化目标函数可表示为

2）总缺水量

区域缺水量的大小或缺水程度对社会各个方面的发展有不同程度的影响，因此采用灌区总缺水量最小作为目标函数[15]，其表达式如下：

3）碳吸收总量

以灌区碳吸收总量最大为目标，作物本身的固碳潜力对于区域水土保持、缓解土壤沙化等均具有重要作用[16]。根据不同种类作物的经济系数和碳吸收率，测算出作物生育期内的碳吸收情况，计算得到每种作物的碳吸收总量[17]，其优化目标函数如下

1.3.2 约束条件

丰收灌区由阿克苏老大河引水，根据灌区用水特点及水资源条件，用“三条红线”作为可供水量约束；灌区耕地因管理不当导致碎块化严重，结合当地的种植条件，用灌区土地政策作为种植面积约束；为维持社会稳定，确保粮食安全，灌区粮食产量需达到全国人均产量。

1）地表水可供水量约束

式中为“三条红线”约束下地表水可供水量，m³。

2）地下水可供水量约束

式中GW为“三条红线”约束下地下水可供水量，m³。

3）土地政策约束

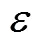
4）粮食产量约束

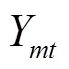
5）作物各生育阶段需水量约束

6）“三条红线”限额下灌区各月用水量约束

7）非负约束

1.4 基于算法优选的模型求解

本文中的多目标优化模型共有3个目标函数和7个约束条件，而传统的蚁群算法、粒子群算法在处理含复杂约束的多目标问题时，易陷入局部最优且Pareto解收敛效果较差。为得到更加合理的全局最优解，本研究通过对比目前在处理多目标优化问题性能较好的NSGA-II（Non-dominated Sorting Genetic Algorithm-II，带精英策略的非支配排序遗传算法）、NSGA-III（Non-dominated Sorting Genetic Algorithm-III，基于参考点的非支配排序遗传算法、MOEA/D（A Multi-Objective Evolutionary Algorithm based on Decomposition，基于分解的多目标进化算法）3种算法，选取最适合本文多目标优化模型的求解算法。

NSGA-II算法是Deb等[18]在原NSGA算法的基础上，提出的一种带有精英策略的非支配排序遗传算法。NSGA-III算法是Jain等[19]在2014年提出处理多个优化目标的进化算法，其主要思路是在NSGA-II的基础上，引入参考点机制，对于非支配并且接近参考点的种群个体进行保留。MOEA/D是Zhang等[20]在2009年提出的基于分解的多目标优化算法，其主要思路是将1个多目标优化问题分解成若干个标量优化子问题，并同时对其进行优化。本研究属于带约束的多目标优化问题，而3种多目标优化算法都没有处理约束的能力，因此分别对其进行改进，将Deb约束准则引入到3种算法中，记作CNSGA-II、CNSGA-III和CMOEA/D算法。

Deb约束支配准则中，根据Pareto支配、约束违反度2种信息来选择较优个体。基于Pareto支配关系的约束处理方法：对于某个解，若其满足约束条件，则称该解为可行解，若不满足，则称之为不可行解。对于不可行解，使用约束违反值（Constraint Violation value，CV）来定量描述其违反约束条件的程度。不可行解的约束违反值计算公式[21]如下：

式中为不等式约束的个数；为等式约束的个数；（）为不等式约束；（）为等式约束。

当（）<0时，（）= −（），否则（）=0。当满足约束条件中任何条件时，即在可行域内，CV（）=0；当不完全满足约束条件时，即不在可行域内，则CV（）≠0。CV值越小，越靠近可行域。

为比较不同算法的性能，分别采用CNSGA-II、CNSGA-III、CMOEA/D算法对同一目标函数求解，选择超体积（Hyper Volume，HV）[22]作为评价算法性能的指标。HV表示算法获得非支配解集与参照点围成的目标空间中区域的体积，HV值越大，说明算法的综合性能越好。其计算公式如下：

1.5 基于熵权-TOPSIS综合评价模型的方案优选

在多目标优化问题中，由于每个目标函数达到最优时所对应的非劣解不同，让决策制定者在最优方案选取时陷入困境。本研究通过构建熵权-TOPSIS综合评价模型，结合当地实际情况建立评价体系，使决策制定者能在Pareto解集中选取最佳方案。

1.5.1 熵权-TOPSIS综合评价模型

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution ）法是一种常见的基于多目标的评价方法，在实际中得到了较为广泛的应用[23-24]。传统的TOPSIS 法主要依赖于专家主观意见定权，可能造成评价结果与实际情况存在一定的偏差[25]。鉴于此，本文借助熵权，对评价对象和正、负理想解的计算方法进行了改进，建立熵权-TOPSIS综合评价模型，使评价结果与真实情况相契合。

具体步骤如下[23-25]：

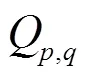
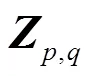
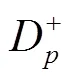
1.5.2 评价指标建立

灌区水资源配置是一个复杂的过程，涉及经济、社会和生态等多方面因素影响，要全面反映各因子对其影响是比较困难的，只能根据具体问题具体分析建立相应的评价模型及指标体系[26]，结合干旱地区水资源开发利用现状和灌区用水特点，考虑到指标的独立性、易得性和资料的局限性，结合研究区特点和优化模型计算的相应数据，构建灌区水资源配置方案评价指标体系，如表1所示。

评价指标体系最上层为目标层，即灌区水资源配置方案；第2层为准则层，包括经济效益、社会效益和生态效益；第3层为指标层，由若干各有侧重又相互关联的具体指标构成。经济效益指标主要从水资源利用程度、产生效益和管理水平等方面考虑，以水资源利用程度为例，地下水和地表水的开发利用程度都与水资源的可持续利用、灌区节水改造规划有着密切的关系[27]，研究区处于水资源短缺地区，提高水资源开发利用程度，合理配置农业用水量，对灌区的可持续发展有着积极的影响，而灌区主要经济收入以种植业为主，为保证当地经济产值，提高灌区人均收入，应考虑灌区经济作物的种植面积，经济效益子系统选用“农业用水比例”、“经济作物占有率”2个指标；社会效益主要从增加GDP、提高农民收入、改善生活质量和推进社会文明进步等方面考虑[28]，研究区处于经济发展落后地区，提高当地人们经济收入是重中之重，而保障当地粮食产量是改善生活质量的重要因素，社会效益子系统选择“人均粮食占有量”、“人均种植业纯收入”2个指标；生态效益指标主要从改善灌区周边环境、水资源保护等方面考虑[29]，降低化肥使用量和提高作物碳吸收量可以缓解灌区生态环境的恶化，因此选择“单位灌溉面积化肥使用量”、“碳吸收总量”作为灌区生态效益子系统的指标。

1.6 数据来源

由《阿瓦提现状调查报告》[30]可知，通过对阿瓦提县2012—2015年地表水实际引用量的收集和分析，结合《塔里木河流域近期综合治理五年实施方案》确定的阿瓦提县丰收灌区地表水限额水量为1.46×108m³，根据现状年调查，灌区2016年实际地表水引水量为1.65×108m³；《阿瓦提县地下水开发建设实施方案》确定的阿瓦提县丰收灌区地下水限额水量为0.11×108m³，根据现状年调查，2016年丰收灌区地下水实际开采量为0.14×108m³。

根据《阿克苏统计年鉴2016》[31]和报告[30]可知，丰收灌区内棉花、玉米和小麦的总灌溉面积为1.80×104hm2，常住人口为31 806人，“三条红线”约束下可用水量为15 730×104m³，综合灌溉利用系数为0.52，当地水价为0.09元/m³，经济净效益为25 269×104元，碳吸收总量为11 364×104kg，作物系数参考相关文献[32-34]。模型所需的作物成本效益数据、“三条红线”约束下地表水和地下水可用水量数据，如表2和表 3所示。

表1 灌区水资源配置方案评价指标体系

表2 灌区作物系数

注：、、分别为水分生产函数的二次项、一次项和常数系数项。

Note:,, andare the quadratic, first, and constant coefficient terms of the water production function, respectively.

表3 “三条红线”约束下丰收灌区地表水和地下水可用水量

2 结果与分析

2.1 灌区水资源优化配置算法优选

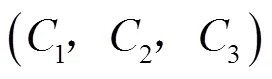
由表4可知，对于本文所建立的多目标优化模型，CNSGA-III算法在HV指标值测试结果中，平均值最大（795.21）且标准差最小（20.36），表明CNSGA-III算法在本研究所建立的多目标优化模型求解中优于其余2种算法。

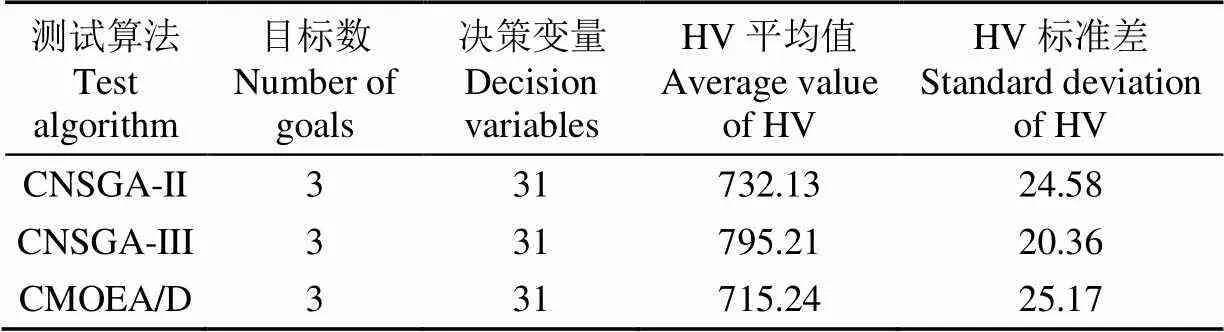
表4 CNSGA-II、CNSGA-III和CMOEA/D算法的HV指标值测试

因此，本研究选用CNSGA-III算法对优化模型求解的Pareto解集合作为灌区水资源配置结果，其Pareto解集合分布图如图2所示，图中每个点表示对应非劣解的大小，每个非劣解都由经济净效益、总缺水量和碳吸收总量共同决定。

2.2 配置方案优选

由图2可知，算法选取的种群规模较大，计算所得的非劣解较多，结合当地实际政策，可依据决策制定者期望缩小方案选取的范围。本研究在充分考虑当地经济落后和严重缺水背景的前提下，选择经济净效益在2.535×108～2.565×108元、总缺水量-0.133×108～-0.129×108m³和碳吸收总量1.186×108～1.187×108kg的共44组非劣解作为待选方案。

采用熵权-TOPSIS综合评价模型对44组非劣解进行评价。评价指标中，农业用水比例1和单位灌溉面积化肥使用量5为逆向指标，其他评价指标均为正向指标。熵权法确定的各个指标权重分别为0.109、0.306、0.174、0.177、0.019、0.215。各方案的指标值及最终得分如图 3和图4所示。

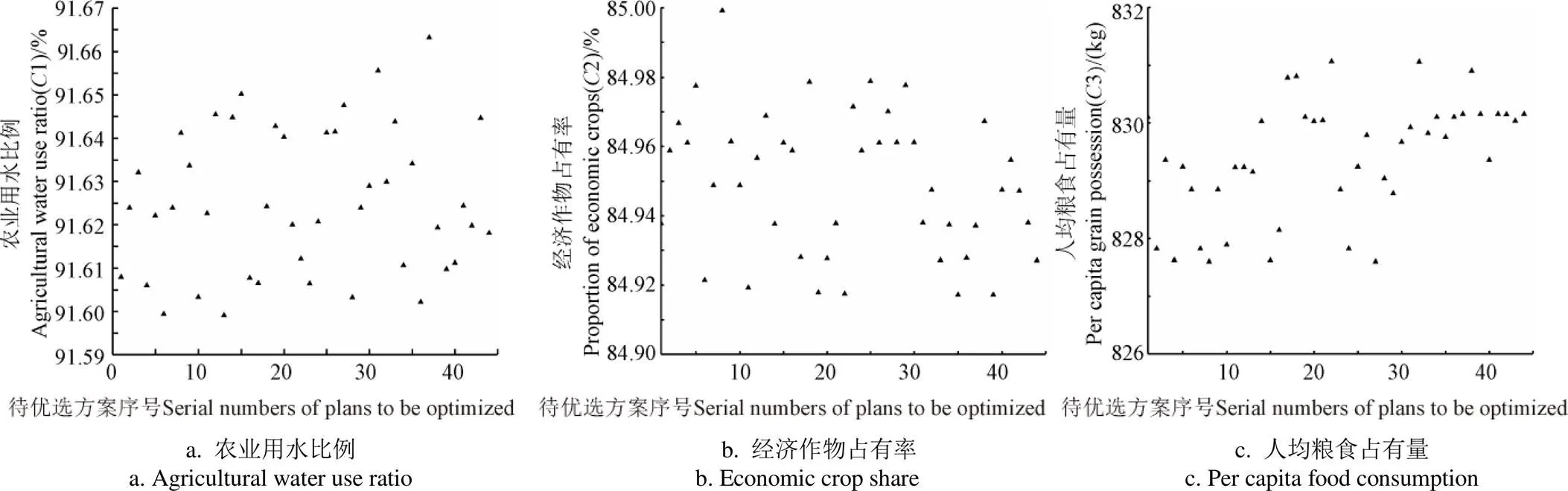
在待优选方案中，方案43的经济净效益最大，为25 636×104元，但其灌区总缺水量高达-1 291×104m³，碳吸收总量仅有11 868×104kg；方案13的灌区总缺水量最小为-1 321×104m³，然而其经济净效益仅有25 385×104元，比最大经济净效益低251×104元，碳吸收总量仅有11 871×104kg；方案21的碳吸收量最大为11 877×104kg，灌区总缺水量高达-1 318×104m³，经济净效益仅有25 374×104元，其经济净效益比方案43低262×104元。可见，在方案选取中，一味追求单方效益达到最优而忽略其他效益是不合理的。

评价模型在综合考虑经济效益、社会效益和生态效益的前提下，依据每个指标信息熵的大小，客观、公平地选取最佳方案。由图4可知，方案40最终得分最高，被选为灌区水资源配置的最优方案，其经济净效益为25 518×104元、灌区总缺水量为-1 319×104m³、碳吸收总量为11 874×104kg。在方案40中，灌区不同作物优化后的种植面积和配水量如表5所示，逐月配水量如表6所示。

由表5可知，优化后，灌区水资源得到充分利用，在各月“三条红线”用水限额下，水资源不仅在各作物间进行合理配置，而且考虑到不同作物在不同生育阶段需水量不同，使各作物关键生育阶段需水量得到保障，相应提高作物产量，使水资源的灌溉效益达到最大化；在满足粮食产量的前提下，棉花种植面积相较优化前增加900 hm2，玉米种植面积减少200 hm2，而小麦种植面积则减少700 hm2，3种作物种植面积配置比例达到较佳水平。

表5 灌区不同作物优化后的种植面积和配水量

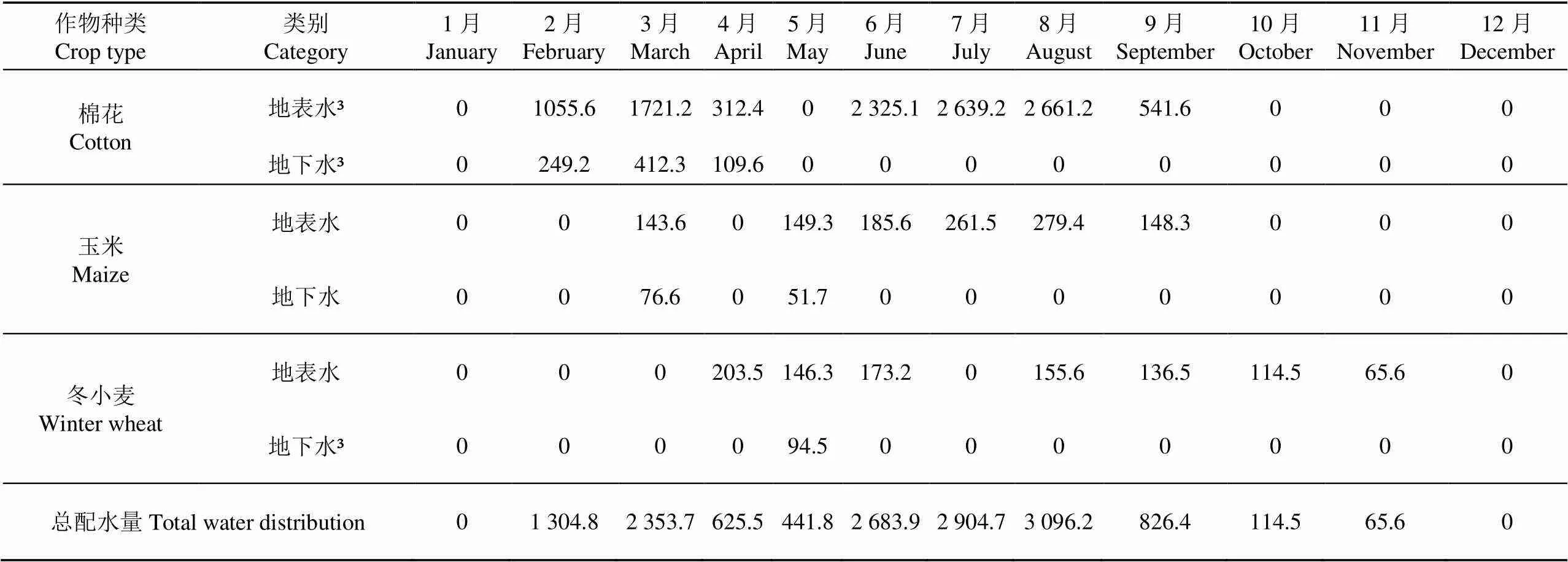
表6 灌区不同作物优化后逐月配水量

优化前，灌区的经济净效益为25 269×104元，“三条红线”约束可用水量为15 730×104m³，碳吸收总量为11 364×104kg；由优选方案40可知，优化后，灌区的经济净效益为25 518×104元、灌区总缺水量为-1 319×104m³、碳吸收总量为11 874×104kg。通过优化计算，经济净效益相较优化前增加 1.0%，灌区总缺水量减少8.4%，碳吸收总量增加4.5%，因此灌区的水资源经过优化配置后，其经济净效益和碳吸收总量得到提高，且能减少灌区农业灌溉用水量。

3 讨 论

传统的灌区水资源多目标优化配置多采用单一方法对优化模型进行求解[11-14]，得到配置方案Pareto解集合，然后灌区管理者在众多的Pareto解集合中根据自己的偏好选择配水方案，传统的配水方法具有强烈的主观性，可能导致配水结果和灌区的实际发展存在冲突。本文将灌区水资源多目标优化配置模型与配水方案优选模型相结合，得到的灌区水资源优化配置方案更加合理，更符合灌区的可持续发展。在前人研究的基础上[35]，将算法优选引入灌区水资源多目标优化配置模型求解中，解决了使用单一算法时存在的算法性能缺陷问题。将MOASPO模型应用于丰收灌区水资源配置中，从得到的配置结果可知，在灌区水资源不足以满足充分灌溉时，模型在非充分灌溉的条件下，通过适当调整灌区内棉花、小麦和玉米的种植结构，降低高耗水且价格低廉作物小麦的种植面积，提高相对耗水量少且经济效益较大作物棉花的种植面积，使各作物关键生育阶段的需水量得到保障，在减少耗水量的同时增加作物产量。

MOASPO模型主要适用于干旱和半干旱区，对于水资源充沛地区，需将多目标优化模型中的决策变量更换，其模型的适用性需进一步验证。

在选择配水方案优选评价体系指标时，存在数据不全和难以定量等困难，综合前人研究成果和本研究中的可量化数据，选取6项指标，其中“碳吸收总量”指标为本研究中新增的生态效益子系统的评价指标。在资料齐全的其他类似灌区，可结合当前灌区的发展趋势，补充相应评价指标的数量。随着学科交叉的日益成熟和机器学习的快速发展，可将机器学习的研究成果引入到农业水土资源多目标优化中。在未来的研究中，可将深度学习中循环神经网络（Recurrent Neural Network，RNN）用于预测未来农业灌溉用水的可用水量，根据HV算法评价指标选择最优进化算法，结合当地实际情况建立合适的评价体系，选择最优的农业水土资源配置方案。

4 结 论

1）针对灌区水资源多目标优化配置模型求解算法的不确定性和最优方案选择问题，构建了基于优选算法的灌区水资源多目标优化配置及方案优选模型（MOASPO）。与传统灌区水资源配置模型相比，MOASPO模型将灌区水资源多目标配置模型和评价模型相结合，得到的最优配水方案，可为灌区管理者提供理论依据和决策支持。

2）分别采用NSGA-II、NSGA-III、MOEA/D算法对多目标优化模型进行求解，通过算法评价指标HV，参考点设置为（-1.151×108，-0.245×106，-0.846×108），CNSGA-III算法的平均值最大为795.21，标准差最小为20.36，最终选择CNSGA-III作为多目标优化模型的最优算法。

3）将所构建的MOASPO模型应用于新疆阿克苏地区阿瓦提县丰收灌区的水资源配置，通过评价筛选，最终选取较优方案。该方案在每月“三条红线”用水限额下，相较于传统配置模型，经济净效益增加1.0%，灌区总缺水量减少8.4%，碳吸收总量增加4.5%。

[1]郭玉丹，何英，彭亮. 基于生态安全的阿瓦提灌区生态需水量研究[J].水资源与水工程学报，2019，30(1)：241-246,253. Guo Yudan, He Ying, Peng Liang. Study on ecological water demand in Awati Irrigation Area based on ecological security[J]. Journal of Water Resources and Water Engineering, 2019, 30(1): 241-246,253. (in Chinese with English abstract)

[2]何英. 干旱区典型流域水资源优化配置研究[D]. 乌鲁木齐：新疆农业大学，2010. He Ying. Research on Optimal Allocation of Water Resources in Typical Watersheds in Arid Areas[D]. Urumqi: Xinjiang Agricultural University, 2010. (in Chinese with English abstract)

[3]戴俊生. 塔里木河流域综合治理工程生态经济效益评价[D].乌鲁木齐：新疆农业大学，2015. Dai Junsheng. Evaluation of the Ecological and Economic Benefits of the Comprehensive Treatment Project of the Tarim River Basin[D]. Urumqi: Xinjiang Agricultural University, 2015. (in Chinese with English abstract)

[4]Kang S, Zhang L, Trout T. Special Issue: Improving agricultural water productivity to ensure food security under changing environments[J]. Agricultural Water Management, 2017, 179: 1-4.

[5]张利平，夏军，胡志芳. 中国水资源状况与水资源安全问题分析[J]. 长江流域资源与环境，2009，18(2)：116-120. Zhang Liping, Xia Jun, Hu Zhifang. Situation and problem analysis of water resource security in China[J]. Resources and Environment in the Yangtze River Basin, 2009, 18(2): 116-120. (in Chinese with English abstract)

[6]许迪，李益农，龚时宏，等. 气候变化对农业水管理的影响及应对策略研究[J]. 农业工程学报，2019，35(14)：79-89. Xu Di, Li Yinong, Gong Shihong, et al. Impacts of climate change on agricultural water management and its coping strategies[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 79-89. (in Chinese with English abstract)

[7]陈卫宾，董增川，张运凤. 基于记忆梯度混合遗传算法的灌区水资源优化配置[J]. 农业工程学报，2008，24(6)：10-13. Chen Weibin, Dong Zengchuan, Zhang Yunfeng. Optimization the allocation of irrigated areas water resources based on memory gradient hybrid genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(6): 10-13. (in Chinese with English abstract)

[8]Zhang Z, Ma H, Li Q, et al. Agricultural planting structure optimization and agricultural water resources optimal allocation of Yellow River Irrigation Area in Shandong Province[J]. Desalination and Water Treatment, 2014, 52(13): 2750-2756.

[9]张展羽，司涵，冯宝平，等. 缺水灌区农业水土资源优化配置模型[J]. 水利学报，2014，45(4)：403-409. Zhang Zhanyu, Si Han, Feng Baoping, et al. Optimal allocation model of agricultural water and soil resources in water-deficient irrigation areas[J]. Journal of Hydraulic Engineering, 2014, 45(4): 403-409. (in Chinese with English abstract)

[10]陈述，邵东国，李浩鑫，等. 基于粒子群人工蜂群算法的灌区渠-塘-田优化调配耦合模型[J]. 农业工程学报，2014，30(20)：90-97. Chen Shu, Shao Dongguo, Li Haoxin, et al. Coupling model of irrigation area canal-pond-field optimal allocation based on particle swarm artificial bee colony algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 90-97. (in Chinese with English abstract)

[11]郭萍，单宝英，郭珊珊. 基于Pareto解集的多目标农业水土资源优化配置模型[J]. 天津大学学报：自然科学与工程技术版，2019，52(10)：1008-1016. Guo Ping, Shan Baoying, Guo Shanshan. Multi-objective optimal allocation model of agricultural water and soil resources based on pareto sets[J]. Journal of Tianjin University (Natural Science and Engineering Technology Edition), 2019, 52(10): 1008-1016. (in Chinese with English abstract)

[12]Anwar A A, Haq Z U. Genetic algorithms for the sequential irrigation scheduling problem[J]. Irrigation Science, 2013, 31(4): 815-829.

[13]岳琼，郭萍，唐毅宽，等.灌区广义水资源不确定性多目标优化配置[J].干旱地区农业研究，2020，38(4)：168-174,183.Yue Qiong, Guo Ping, Tang Yikuan, et al. Multi-objective optimal allocation of generalized water resources in irrigation district under uncertainty[J]. Agricultural Research in Arid Areas, 2020, 38(4): 168-174,183. (in Chinese with English abstract)

[14]Chen J, Ding T, Li M, et al. Multi-objective optimization of a regional water-energy-food system considering environmental constraints: A case study of Inner Mongolia, China[J]. International Journal of Environmental Research and Public Health, 2020, 17(18): 6834.

[15]张志军，黄宝连. 基于水资源优化配置的多目标决策模型探析[J].水利规划与设计，2011(3)：22-25. Zhang Zhijun, Huang Baolian. Multi-target decision-making model analysis based on optimal disposition of water resources[J]. Water Resources Planning and Design, 2011(3): 22-25. (in Chinese with English abstract)

[16]谭倩，缑天宇，张田媛，等. 基于鲁棒规划方法的农业水资源多目标优化配置模型[J]. 水利学报，2020，51(1)：56-68. Tan Qian, Gou Tianyu, Zhang Tianyuan, et al. Multi-objective optimal allocation model of agricultural water resources based on robust planning method[J]. Journal of Hydraulic Engineering, 2020, 51(1): 56-68. (in Chinese with English abstract)

[17]韩召迎，孟亚利，徐娇，等. 区域农田生态系统碳足迹时空差异分析：以江苏省为案例[J]. 农业环境科学学报，2012，31(5)：1034-1041. Han Zhaoying, Meng Yali, Xu Jiao, et al. Spatial and temporal differences in carbon footprint of regional farmland ecosystems: A case study of Jiangsu Province[J]. Journal of Agricultural Environment Sciences, 2012, 31(5): 1034-1041. (in Chinese with English abstract)

[18]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[19]Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, part II: Handling constraints and extending to an adaptive approach[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 602-622.

[20]Zhang Q, Li H. MOEA/D: A multi-objective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731.

[21] Deb K. An efficient constraint handling method for genetic algorithms[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2/3/4): 311-338.

[22]Tian Y, Cheng R, Zhang X, et al. Diversity assessment of multi-objective evolutionary algorithms: Performance metric and benchmark problems[J]. IEEE Computational Intelligence Magazine, 2019, 14(3): 61-74.

[23]朱珠，张琳，叶晓雯，等. 基于TOPSIS方法的土地利用综合效益评价[J]. 经济地理，2012，32(10)：139-144. Zhu Zhu, Zhang Lin, Ye Xiaowen, et al. Evaluation of comprehensive benefits of land use based on TOPSIS method[J]. Economic Geography, 2012, 32(10): 139-144. (in Chinese with English abstract)

[24]雷勋平，Robin Qiu，刘勇. 基于熵权TOPSIS模型的区域土地利用绩效评价及障碍因子诊断[J]. 农业工程学报，2016，32(13)：243-253. Lei Xunping, Robin Qiu, Liu Yong. Regional land use performance evaluation and barrier factor diagnosis based on entropy weight TOPSIS model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 243-253. (in Chinese with English abstract)

[25]鲁春阳，文枫，杨庆媛，等. 基于改进TOPSIS法的城市土地利用绩效评价及障碍因子诊断：以重庆市为例[J]. 资源科学，2011，33(3)：535-541. Lu Chunyang, Wen Feng, Yang Qingyuan, et al. Urban land use performance evaluation and barrier factor diagnosis based on improved TOPSIS method: Taking Chongqing as an example[J]. Resources Science, 2011, 33(3): 535-541. (in Chinese with English abstract)

[26]冯峰，许士国. 灌区水资源综合效益的改进多级模糊优选评价[J]. 农业工程学报，2009，25(7)：56-61. Feng Feng, Xu Shiguo. Improved fuzzy-optimal multi-level evaluation for comprehensive benefit of water resources in irrigation area[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(7): 56-61. (in Chinese with English abstract)

[27]张燕妮. 大型灌区水资源综合效益评价[D]. 杨凌：西北农林科技大学，2010. Zhang Yanni. Evaluation of Comprehensive Benefits of Water Resources in Large-scale Irrigation Area[D]. Yangling: Northwest A&F University, 2010. (in Chinese with English abstract)

[28]袁伟. 面向可持续发展的黑河流域水资源合理配置及其评价研究[D]. 杭州：浙江大学，2009.Yuan Wei. Research on the Rational Allocation and Evaluation of Water Resources in the Heihe River Basin for Sustainable Development[D]. Hangzhou:Zhejiang University, 2009. (in Chinese with English abstract)

[29]王浩，尹明万，秦大庸，等. 水利建设边际成本与边际效益评价[M]. 北京：科学出版社，2004：54-60.

[30]张黎明. 阿瓦提现状调查报告[R]. 新疆：新疆兵团勘测设计院，2017.

[31]阿克苏统计局. 国家统计局阿克苏调查队. 阿克苏统计年鉴2010-2016[M]. 阿克苏：阿克苏市统计局，2016.

[32]胡顺军，王仰仁，康绍忠，等. 棉花水分生产函数Jensen模型敏感指数累积函数研究[J]. 沈阳农业大学学报，2004，35(5/6)：423-425.Hu Shunjun, Wang Yangren, Kang Shaozhong, et al. Cumulative function of sensitive index of jensen’s crop water production model for cotton[J]. Journal of Shenyang Agricultural University, 2004, 35(5/6): 423-425. (in Chinese with English abstract)

[33]孙建光，韩桂兰. 塔里木河流域基于作物水分生产函数的农业水价需求效应分析[J]. 水利水电科技进展，2009，29(4)：24-26. Sun Jianguang, Han Guilan. Demand effect analysis of agricultural water price based on crop water production function in Tarim River Basin[J]. Progress in Water Resources and Hydropower Science and Technology, 2009, 29(4): 24-26.

[34]雷志栋，胡和平，杨诗秀，等. 叶尔羌河灌区冬小麦灌溉试验与分析[J]. 灌溉排水，1999(2)：3-5.Lei Zhidong, Hu Heping, Yang Shixiu, et al. Water equilibrium model of agriculture-non-agriculture area based on soil water movement[J]. Irrigation and Drainage, 1999(2): 3-5. (in Chinese with English abstract)

[35]单宝英，郭萍，张帆，等. 基于遗传算法与方案优选的多目标优化模型求解方法[J].中国农业大学学报，2019，24(6)：157-165. Shan Baoying, Guo Ping, Zhang Fan, et al. A multi-objective optimization model solving method based on genetic algorithm and scheme optimization[J]. Journal of China Agricultural University, 2019, 24(6): 157-165. (in Chinese with English abstract)

Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang

He Ying, Tang Xiaoyu, Peng Liang, Ju Jinhao

(1.,,830052,;2.,830052,)

Severe global water shortages have posed a great challenge on modern agriculture as ever-increasing demand for water due to the population and economic growth. Therefore, it is necessary to scientifically allocate the limited water resources in main irrigation areas, further to improve the utilization rate of agricultural water for the local economy and ecosystem. Taking Fengshou Irrigation Area in Awati County, Aksu Prefecture, Xinjiang of China as the research area, a multi-objective optimal allocation of water resources was established to obtain an optimal selection model (Multi-Objective optimal allocation model of water resources in irrigation area based on Algorithm Selection and Plan Optimization, MOASPO). The economic, social and ecological development indicators were considered, and the evaluation system of water resource allocation scheme in Fengshou Irrigation Area was established, in order to obtain better net economic benefits in the irrigation area with smaller agricultural water consumption. Two procedures were included in the model: 1) To select the optimal solution for the multi-objective optimal allocation model of water resources in the irrigation area, where the NSGA-II, NSGA-III, and MOEA/D were utilized for each Pareto solution, and then the HV algorithm evaluation index was selected to evaluate each Pareto solution under a unified reference point, and finally to select an optimal solution. 2) To select the best allocation plan of water resources suitable for the specific irrigation area. The candidates were taken from the Pareto solution set, thereby constructing an optimal evaluation system for water resources allocation plans in irrigation areas, combining the local actual conditions from economic, social, and environmental benefits. Specifically, the subsystem of economic benefit included two indicators: “per capita net income from planting industry” and “economic crop occupancy rate”, while the subsystem of social benefit included two indicators: “per capita food occupation” and “agricultural water use ratio”. Meanwhile, the eco-environmental subsystem included two indicators: “fertilizer use per unit of irrigation area” and “total carbon absorption”. An entropy weight-TOPSIS comprehensive model was used to evaluate the options to be selected, and finally to determine the optimal allocation plan of water resources. The results show that the cotton planting area increased by 900hm2under the appropriate grain output, whereas, the planting area of maize and wheat reduced by 200 and 700 hm2, respectively, indicating an optimal proportion of crops planting area. After optimization, the net economic benefit was 255.18 million Yuan, while the total shortage of agricultural water was reduced by 13.19 million m³, and the carbon sequestration of crops was 118.74 million kg. The net economic benefit increased by 1.0%, while the total shortage of agricultural water was reduced by 8.4%, and the amount of carbon sequestered by crops increased by 4.5%, compared with the traditional allocation plan. The proposed model and optimized plan can provide a potential reference to formulate an allocation plan of water resources in the arid irrigation areas.

water resources; algorithms; multi-objective; uncertainty; evaluation model; irrigation area

何英，唐晓宇，彭亮，等. 南疆丰收灌区水资源多目标优化配置方案优选[J]. 农业工程学报，2021，37(6)：117-126.doi：10.11975/j.issn.1002-6819.2021.06.015 http://www.tcsae.org

He Ying, Tang Xiaoyu, Peng Liang, et al. Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(6): 117-126. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.06.015 http://www.tcsae.org

2020-09-27

2021-03-02

国家自然科学基金项目（51969029，51569031）；新疆水利科技专项资金项目（XSKJ-2020-04）

何英，博士，副教授，研究方向为干旱区水文模拟与水资源评价。Email：xjheying@126.com

10.11975/j.issn.1002-6819.2021.06.015

S274.3

A

1002-6819(2021)-06-0117-10