箱梁剪力滞效应一维有限元模型及评价方法

黄 俊,胡志祥,李佳津

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

箱梁的剪力滞效应最显著的体现就是截面法向应力不均匀,通常顶板与腹板交界处的应力比理论计算出的应力要大很多。目前,国内外建造了大量的大跨箱型梁桥、悬臂斜拉桥等,剪力滞效应都较为突出[1-2]。另外,高层建筑中的筒体结构[3-4]在横向力作用下也会出现剪力滞效应。在设计中忽略剪力滞效应的影响,可能会导致结构的局部应力过大,甚至导致结构整体破坏,因此剪力滞效应得到结构工程师的关注。

对箱梁剪力滞效应的研究方法最常见的有解析法[5]、数值分析方法[6]和模型试验[7],其中数值分析方法随着计算机性能的不断提高,应用越来越广泛。三维实体有限单元法作为一种数值方法,受到众多商业软件的支持,可用于详细分析剪力滞效应对箱梁受力及变形的影响,但其受单元选取、网格划分的影响比较大,计算精度易受主观因素的影响,且给出的应力结果无法直接指导工程设计。

目前关于箱梁剪力滞效应,对箱梁进行一维有限元分析的相关文献较丰富。文献[8]修正了传统箱梁剪力滞理论中的纵向位移表达式,提出考虑箱梁附加挠度的箱梁一维有限元模型,该模型以总挠度、附加挠度及两者导数作为单元位移参数,总挠度未知量包含了初等梁挠度和附加挠度;文献[9-10]分离出了剪力滞效应引起的附加挠度,并将其作为广义位移,推导出箱梁附加挠度的解析表达式。上述2种计算方法的区别在于是否分离出了附加挠度,有必要对这2种计算方法进行对比分析。本文在文献[8,10]基础上,将初等梁挠度与附加挠度分离,推导了箱梁的一维离散有限元模型单元参数,同时研究了二次、三次抛物线型剪力滞翘曲位移函数和不同附加挠度形函数对计算结果的影响。

此外,评价箱梁的剪力滞效应具有重要工程意义,目前已有多种分析方法[11-13]。传统理论利用箱梁实际应力和按初等梁理论计算出来的应力来定义剪力滞系数[11],由于箱梁截面上的应力取值往往不唯一,导致同一截面上有不同的剪力滞系数。文献[12]用箱梁的有效宽度来反映剪力滞效应,但对有效翼缘宽度的确定是具有统计意义的均值,使用时不可避免地存在较大误差。本文通过计算发现,总挠度二阶导数和初等梁挠度二阶导数的比值与空间有限元模型中的应力不均匀程度趋势相互符合,因此提出用总挠度和初等梁挠度二阶导数的比值作为剪力滞效应表征指标。

最后,为研究移动荷载作用下箱梁的剪力滞效应,取箱梁在移动荷载处于不同位置时同一截面处最大、最小应力形成该梁的应力包络。通过取应力包络的方式可分别作出考虑剪力滞效应时箱梁截面的应力包络及仅考虑初等梁计算结果的应力包络,通过应力包络对比可以直观地反映箱梁剪力滞效应的分布情况。

1 剪力滞翘曲位移函数

箱梁横截面尺寸简图如图1所示。

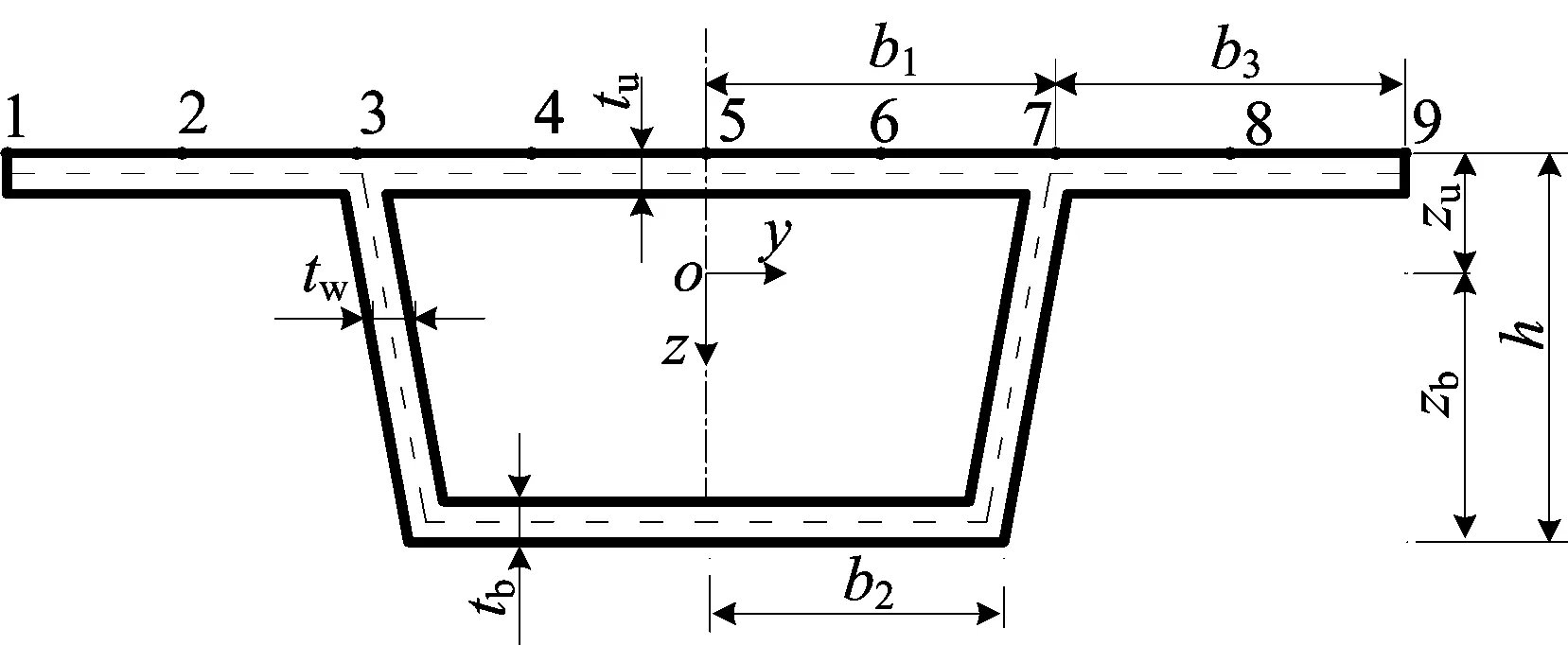
图1 箱梁横截面尺寸简图

本文将挠度中初等欧拉梁挠度ω和箱梁剪力滞效应引起的附加挠度ωa分别考虑,故横截面上任一点的纵向位移u(x,y,z)可表达为:

u(x,y,z)=-zω′(x)-f(y,z)ωa′(x)

(1)

f(y,z)=z-ηfζ(y,z)

(2)

fζ(y,z)=

(3)

其中:ω′、ωa′分别为ω、ωa的一阶导数;f(y,z)为相应附加转角ωa′的剪力滞广义翘曲位移函数;η为待定系数;fζ(y,z)为剪力滞翘曲位移函数;m取值为2、3;z分别取zu、zb,即上、下翼缘分别到截面形心的距离;At、Ac、Ab分别为箱梁顶板面积、悬臂板面积、底板面积。

该箱梁的形心坐标为:

yc=0

(4)

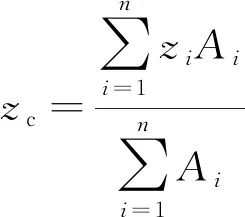
(5)

横截面上任意一点的正应力σ(x,y,z)和切应力τ(x,y,z)表达式为:

-Ezω″(x)-Ef(y,z)ωa″(x)

(6)

(7)

其中:-Ezω″(x)为相应初等梁的弯曲应力;-Ef(y,z)ωa″(x)为剪力滞翘曲应力σa,即

σa=-Ef(y,z)ωa″

(8)

箱形横截面上的弯矩只由相应初等梁弯曲应力合成,而σa在箱梁横截面上不合成弯矩[8],即

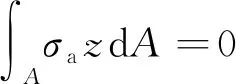
(9)

将(8)式代入(9)式,并注意y轴为水平形心轴,则得:

η=I/Izζ

(10)

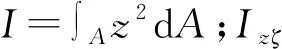
定义σa相应的广义力矩Ma为:

(11)

将(8)式代入(11)式得:

Ma=-EIfωa″

(12)

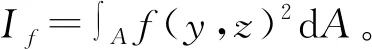
If=η2Iζ-I

(13)

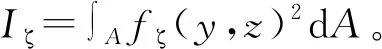
根据(1)式定义的纵向位移函数,可以建立在外荷载作用下的总势能泛函:

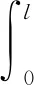
(14)

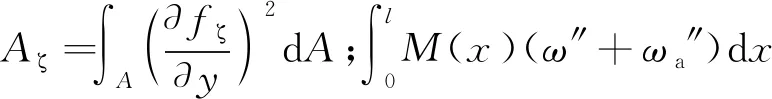
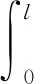
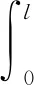
(15)

对(14)式求一阶变分得:

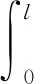
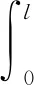
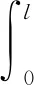
(16)

则箱梁受力的变形微分方程为:

EIω‴′-q=0

(17)

EIfωa‴′-η2GAζωa″-q=0

(18)

剪力滞控制微分方程(18)式可化为:

ωa‴′-k2ωa″=q/(EIf)

(19)

(20)

由材料力学和(19)式，可以引入如下3类边界条件:

(1)固定边条件,即

ωa=0,ωa′=0,ω=0,ω′=0

(21)

(2)简支边条件,即

ωa=0,ωa″=0,ω=0,ω″=0

(22)

(3)自由端条件,即

ωa″=0,ωa‴-k2ωa′=0,ω″=0

(23)

2 箱梁剪力滞效应一维有限元模型

为便于计算微分方程(17)式、(18)式中的未知挠度和附加挠度,本文推导了箱梁的一维离散有限元模型单元参数。

为便于对比,该有限元模型形式与文献[10]中的相似,区别在于本文模型分离了初等梁挠度和附加挠度,其刚度方程为:

Keδe=Pe

(24)

其中:Ke为单元刚度矩阵;δe为单元节点位移矩阵;Pe为单元荷载矩阵。

2.1 箱梁单元节点位移

箱梁的单元节点位移包括初等梁挠度、附加挠度及它们的转角,各位移方向如图2所示。节点位移定义如下:

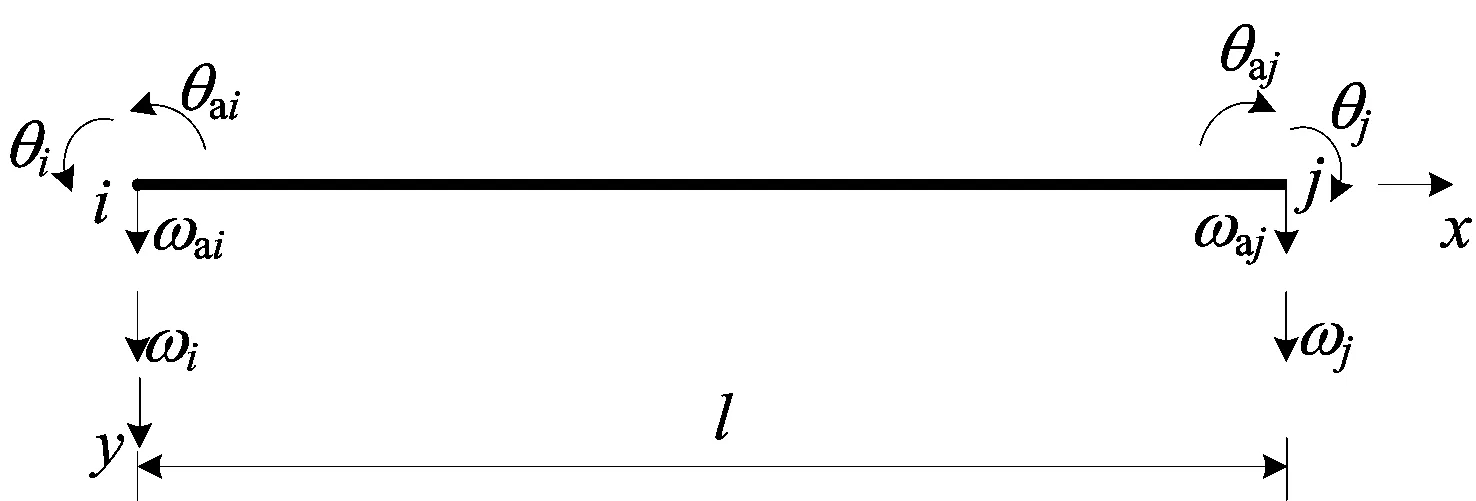
图2 箱梁单元的节点位移

(25)

2.2 箱梁单元荷载矩阵

与单元节点位移相对应,箱梁单元节点荷载为:

(26)

其中:N为单元初等梁挠度和附加挠度的形函数;Te为外荷载向量。当外荷载为均布荷载时,有

(27)

当外荷载为集中荷载时,只需要在荷载矩阵中相对应的节点上施加即可。

当ω(x)、ωa(x)采用Hermite多项式作为形函数时,有

(28)

(29)

当ωa(x)采用双曲函数作为形函数时,有

(30)

4(coshkle-klesinhkle-1)]/(2k2λ)

(31)

其中:荷载矩阵中其余元素与(29)式相同;N1～N4为三次Hermite形函数;N5～N8为双曲形函数[9];λ=klesinhkle+2-2coshkle。

2.3 箱梁单元刚度矩阵

将总势能泛函(14)式写成矩阵形式为:

(32)

(33)

(34)

考虑到

αe=Nδe

(35)

βe=Bδe

(36)

得到:

(37)

(38)

其中:Ke为对称矩阵;B为形变矩阵。

使用Hermite多项式作为ω(x)和ωa(x)形函数时,有

使用双曲函数作为ωa(x)的形函数时,有

k12=k16=-k25=-k56=

3 箱梁剪力滞效应评价方法

为了评价箱梁的剪力滞效应,文献[8]提出用总挠度和初等梁挠度比值定义剪力滞系数,即

(39)

本文通过计算发现,λω不能真实反映实体三维有限元模型中的剪力滞效应,而截面应力与初等梁挠度和附加挠度的二阶导数有关。为了更加准确地描述箱梁剪力滞效应,分析箱梁正应力的构成,本文采用挠度二阶导数的比值作为箱梁一维有限元模型剪力滞效应的评价指标,即

(40)

其中,ω″、ωa″由(36)式求得。

为了反映实体三维有限元模型中截面应力的不均匀程度,定义截面应力不均匀系数λz为:

(41)

其中:K为顶、底板截面划分的层数;σi为在第i层的各节点正应力。

因此可通过计算λω″与λz,对比其趋势以证明用挠度二阶导数比值作为描述箱梁剪力滞效应评价指标的合理性。

4 算例分析

选取图1所示的梯形截面箱梁,跨度l=40 m,泊松比为ν=0.2,弹性模量E=30 GPa,θ=14°,承受均布荷载q=10 kN/m。截面尺寸如下:h=2.775 m,tw=0.35,tu=0.25 m,tb=0.30 m,b1=3 m,b2=2 m,b3=3 m。

箱梁边界条件考虑两端固支、两端简支及悬臂3种情况,x为纵向坐标。

4.1 一维有限元梁单元模型计算结果

首先,计算不同边界条件下总挠度和附加挠度,并将本文方法与文献[8-9]方法求得的结果进行对比,如图3所示。从图3可以看出,本文方法与文献[8-9]方法计算箱梁节点位移参数结果吻合良好。

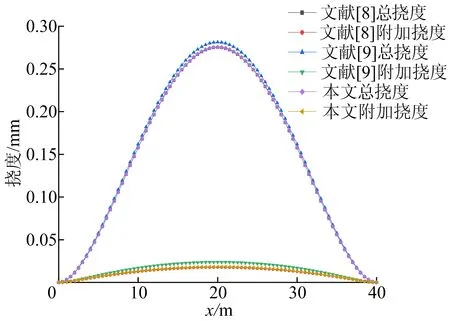
(a) 两端固支箱梁

利用本文一维离散有限元模型计算两端固支跨中截面顶板的应力分布,与文献[8] 结果进行对比,如图4所示。由图4可知，2种方法应力最大差值仅为1.3%左右。因此,本文方法计算的应力和挠度与文献[8]结果基本一致。

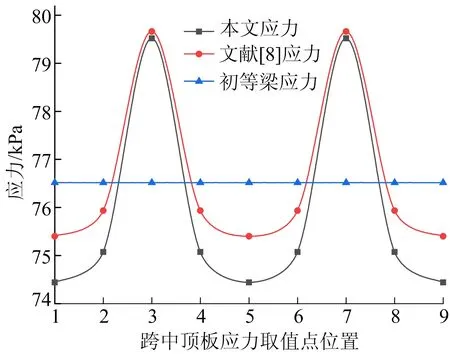
图4 两端固支箱梁本文与文献[8]应力计算结果对比

其次,探索剪力滞翘曲位移函数为二次抛物线型或三次抛物线型,以及附加挠度形函数为Hermite多项式函数或双曲函数时对计算两端固支箱梁附加挠度、初等梁挠度的影响。4种组合下附加挠度计算结果见表1所列。

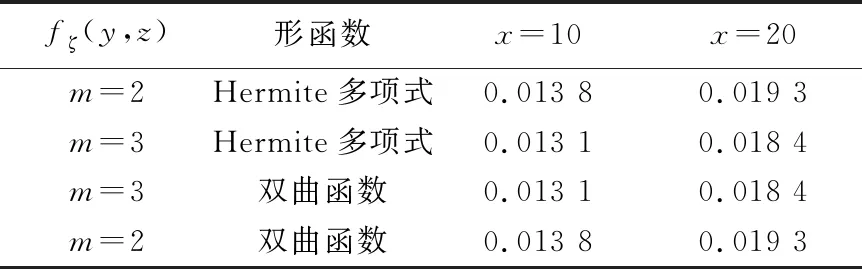
表1 沿梁长方向两端固支箱梁附加挠度计算结果 m

当x取10、20时,欧拉梁挠度计算结果分别为0.145、0.258 m。由表1结果可知：附加挠度采用不同的形函数时,计算结果是一样的,因此用双曲函数和Hermite多项式函数作为形函数,都可以得到比较精确的结果;采用二次或三次抛物线型剪力滞翘曲位移函数,附加挠度基本吻合,因此分析箱梁的剪力滞效应时,选择剪力滞翘曲位移函数为二次或三次抛物线型均可以。

4.2 剪力滞效应评价

为了更加准确地评价剪力滞效应,分别计算了两端固支箱梁挠度和初等梁挠度零阶导数比值λω、一阶导数比值λω′、二阶导数比值λω″,结果如图5所示。从图5可以看出:λω、λω′、λω″作为剪力滞系数,在跨中附近几乎没有剪力滞效应;在支座两端附近,λω″出现突变,这是由于在x=8.45 m和x=31.55 m处,弯矩值为0,初等梁挠度二阶导数为0,因此出现突变的情况。

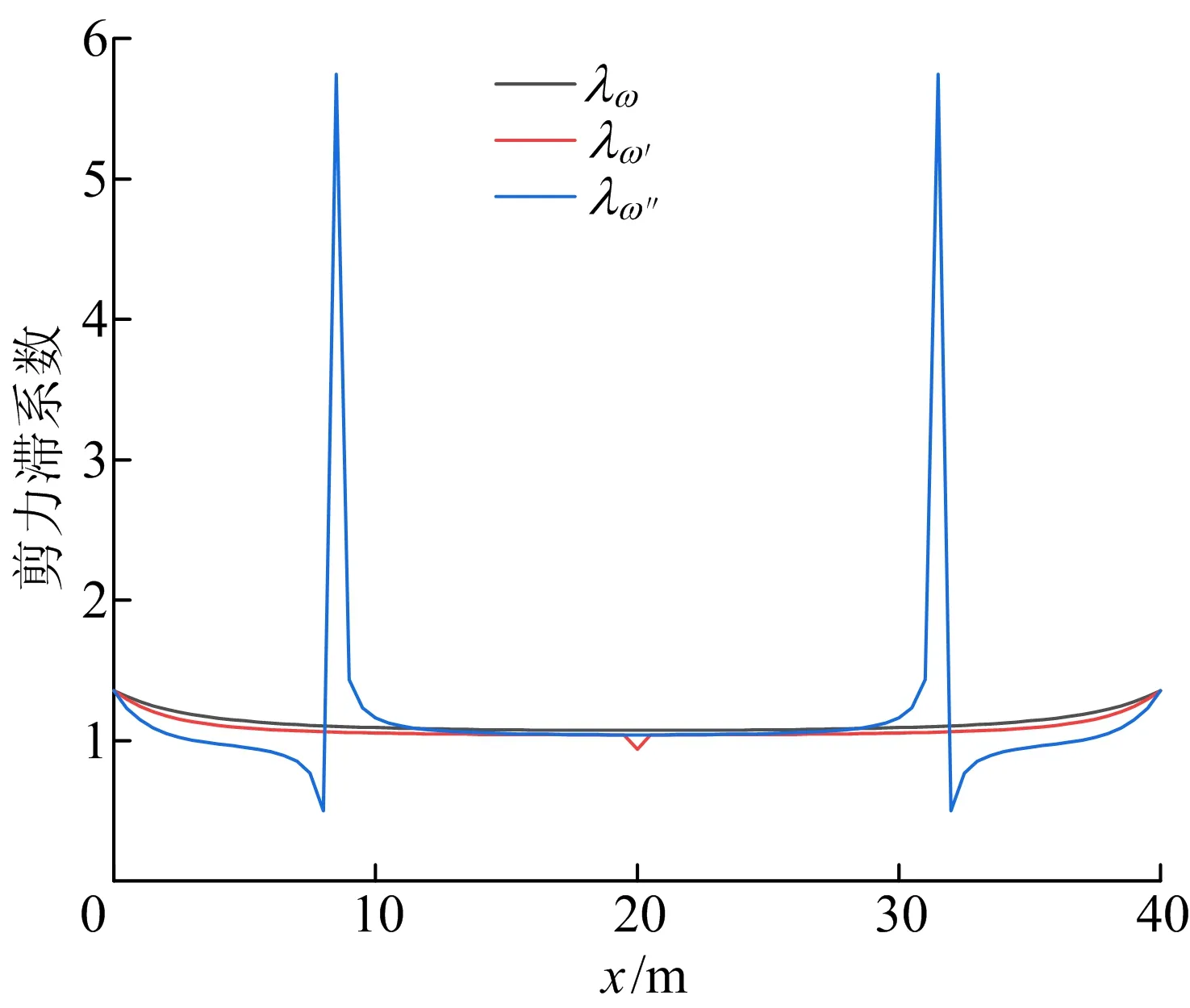
图5 剪力滞评价指标

建立三维实体有限元模型,将顶板和底板沿着截面横向均匀划分,统计各截面顶板和底板的应力不均匀程度,然后与λω″对比,结果如图6所示。

从图6可以看出，λω″与λz出现突变的位置相同,图形趋势一致,因此用挠度二阶导数的比值定义剪力滞效应评价指标更具有物理意义。

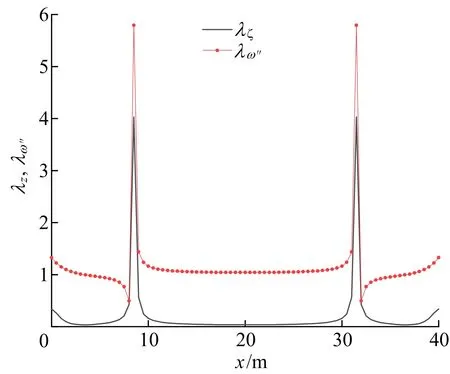
图6 λω″与λz对比

4.3 考虑剪力滞效应的应力包络

在实际桥梁的受力中,汽车活载和桥梁自重是设计中最重要的考虑因素。而箱梁顶板与腹板交界处剪力滞效应最明显,也是箱梁最薄弱的位置,因此可选择此处(图1中点3位置)分析两端固支箱梁应力包络。移动荷载沿桥梁纵向等距离移动,大小为200 kN。在绘制应力包络图时,首先计算各截面处考虑剪力滞效应的应力最大值和最小值,再计算各截面处初等梁应力最大值和最小值。通过绘制应力包络,可直观地分析箱梁沿梁长方向的剪力滞效应。

箱梁在移动荷载下初等梁弯矩包络图如图7所示。从图7可以看出,在移动荷载作用下,箱梁截面负弯矩(Mu)包络两端弯矩较大,截面正弯矩(Md)包络箱梁跨中的弯矩较大。

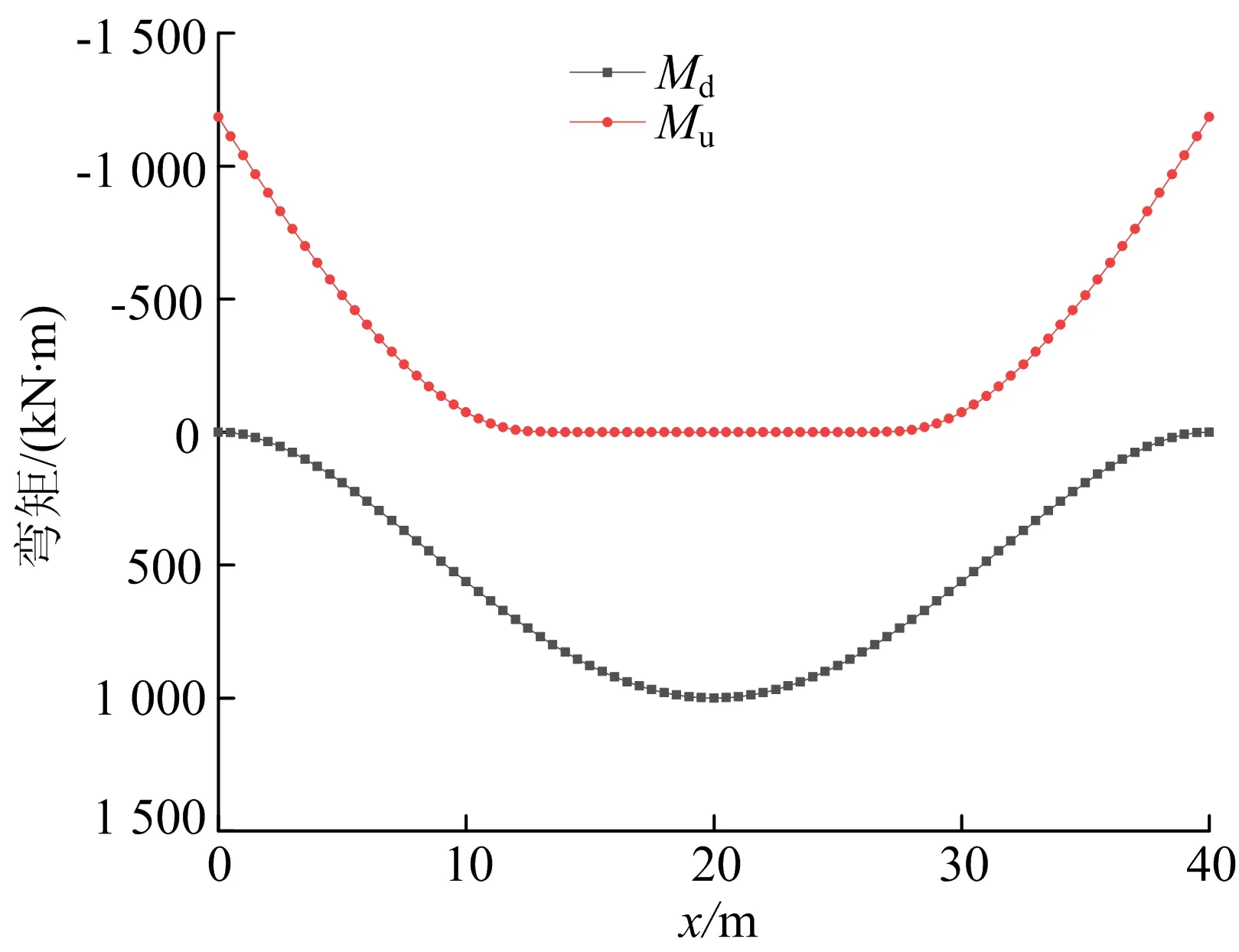
图7 箱梁在移动荷载下初等梁弯矩包络图

箱梁在移动荷载下的应力包络图如图8所示。从图8可以看出,在应力包络图中,考虑剪力滞效应的箱梁应力始终包裹着初等梁应力，由此可见考虑剪力滞效应对工程安全有重要意义。

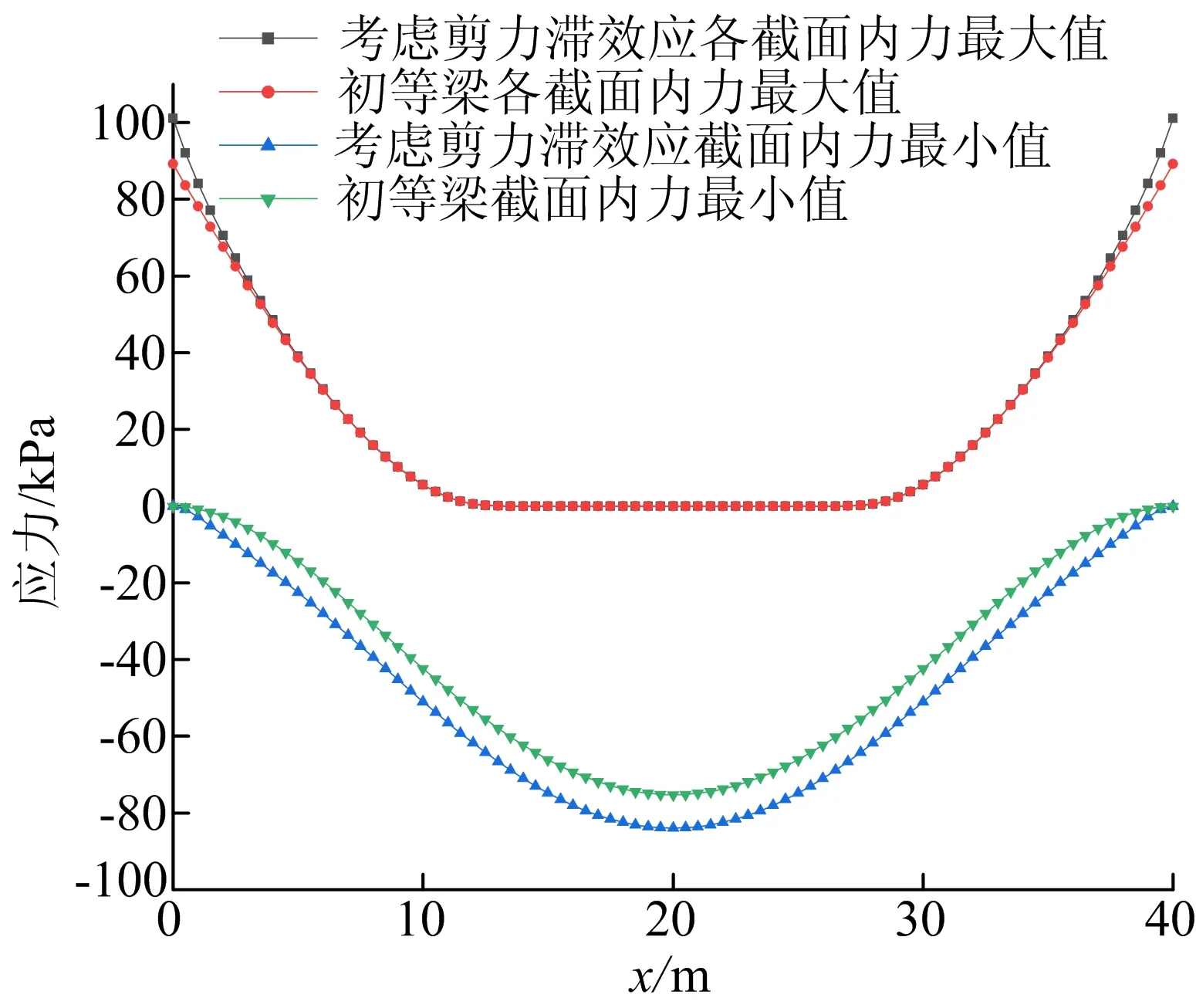
图8 箱梁在移动荷载下的应力包络图

在箱梁两端,截面负弯矩较大,考虑剪力滞效应时应力为101.1 kPa,而未考虑剪力滞效应时应力为89.2 kPa,两者比值为1.13，这反映了该箱梁在端部固支处需考虑剪力滞导致的应力放大比例。在箱梁跨中,截面正弯矩突出,考虑剪力滞效应时应力为83.9 kPa,而未考虑剪力滞效应时应力为75.2 kPa,两者比值为1.12，这说明箱梁在跨中受车辆荷载作用时,需考虑剪力滞导致的正应力放大。在跨中和端部,上述2个应力比值数值接近,其原因是施加于箱梁跨中的竖向荷载相当于一个反向支座,因而其截面剪力滞效应与两端相近。

5 结 论

本文将附加挠度和初等梁挠度相互分离,对箱梁剪力滞效应进行了理论研究,用最小势能原理建立了考虑剪力滞效应的箱梁一维有限元模型。采用不同剪力滞翘曲位移函数、不同附加挠度形函数推导了有限元单元参数,并通过算例对比了计算结果,结果表明:采用双曲函数或Hermite多项式函数作为单元形函数都可得到较为精确的结果;采用二次抛物线函数或三次抛物线函数作为剪力滞翘曲位移函数时计算结果亦较为接近。以双曲函数作为形函数时理论推导及有限元单元参数表达较为复杂,本文建议采用Hermite多项式函数作为单元形函数。

为了评价箱梁的剪力滞效应,提出了采用总挠度与初等梁挠度两者二阶导数的比值作为剪力滞效应的评价指标。该指标与三维实体有限元模型截面应力分布不均匀程度相互符合,表明用总挠度二阶导数和初等梁挠度二阶导数的比值评价剪力滞效应更具有物理意义。

最后,利用本文提出的一维有限元模型,计算了在移动荷载作用下箱梁的应力,绘出了考虑剪力滞效应时箱梁的应力包络图,利用该图可直观对比移动荷载下的剪力滞效应及最不利应力分布。下一步可用该方法研究在不同工况及边界条件下的箱梁应力分布。