箱桁组合斜拉桥同步顶推中的桁梁施工方法研究
2021-06-01梁栋,李亮,刘菁
梁 栋,李 亮,刘 菁
(河北工业大学 土木与交通学院,天津 300401)
0 引 言
裕溪河特大桥为双塔钢箱桁组合梁斜拉桥,根据施工条件、工期要求,边跨采用箱桁同步顶推施工方法,即桁梁杆件的拼装、下弦箱梁的安装以及梁的顶推施工同时进行。目前箱桁组合梁顶推施工主要有2种思路,即整体吊装法和桁梁杆件散拼法。整体吊装法在工厂内将桁梁和箱梁拼装成整体,再运送到现场整体吊装,减少了现场的工作量,但整体吊装梁段质量重、体积大,需要的存梁场地大,同时整体拼装控制点较多,难度大,如天兴洲公铁两用斜拉桥最重梁段达700 t,长宽高为14 m×30 m×15.2 m[1-2]。在桁梁散拼法中,钢箱梁能够为桁梁杆件的拼装提供平台,可降低高空作业风险,桁梁以单根杆件拼装,为运输提供方便,并减小吊装设备压力,例如安庆长江大桥、洞庭湖铁路斜拉桥等均采用这种方法施工[3-4]。
国内外学者对顶推施工进行了深入研究。文献[5]对顶推过程中钢箱梁的应力分布、应力超限原因及改善方法进行了模拟分析;文献[6]对箱梁顶推过程进行了有限元分析,并指导了临时墩、导梁等结构的设计;文献[7]用传递矩阵法研究了曲率半径、弯曲扭转刚度比等参数对弯桥顶推施工的影响;文献[8]用数值优化法,以导梁、预应力费用为目标函数,优化了顶推施工的混凝土箱梁截面尺寸、主梁前端预应力和导梁参数;文献[9]研究了顶推施工完成后,千斤顶处钢箱梁在落梁过程中的力学特征。同时,许多学者对箱桁组合斜拉桥的施工方法进行了研究。文献[10]研究了芜湖长江公铁大桥“浮吊辅助架设墩顶节段+桥面架梁吊机悬臂架设”的施工方案,对箱桁梁的悬臂拼接施工进行了详细介绍;文献[11]针对箱桁斜拉桥上、下弦杆纵向变形差的问题进行了研究,通过对上弦杆的长度补偿实现了桁梁的无应力安装;文献[4]对先箱后桁两步施工法进行了可行性研究,并提出:先单独安装并合拢钢箱梁,然后调整斜拉索力使钢箱梁处于平直状态,最后安装桁梁的施工方法。“先箱后桁法”虽然能够较好控制安装误差,但是箱梁和桁梁施工不能同时进行,这就延长了施工工期,增加了施工成本。但是,针对箱桁组合斜拉桥主梁顶推同步施工方法的研究还不多。
裕溪河特大桥工期紧、任务重,主梁从开始施工到合拢仅有13个月的工期,如果采用常规的“先箱后桁法”,将无法按期完工。为此,该桥主梁在顶推过程中采用了“箱桁同步施工”方法,即在箱梁顶推期间同步安装桁梁,以大幅减少工期。
众所周知,在顶推过程中,不断变化的钢箱梁的变位,极易造成桁梁与钢箱梁之间的变形不协调,即在桁梁施工时箱梁已产生变形,箱梁变形会导致桁腹杆位移,这使得上弦杆安装困难。为此,本文针对裕溪河桥边顶推边安装桁梁的施工方法,研究了箱梁节段数量、桁梁安装顺序等因素对上弦杆安装精度的影响,提出了一种避免使用辅助措施的快速施工方法,为裕溪河特大桥顺利合拢提供了技术支持。
1 裕溪河特大桥
1.1 概况
主桥采用(60+120+324+120+60) m双塔箱桁组合斜拉桥,如图1所示(单位为m)。主梁为箱桁结构,主桁为不带竖杆的华伦式桁架,横向采用2片主桁平行布置,主桁中心距14.0 m,桁高12.0 m,箱梁为正交异性板结构,采用带风嘴的单箱七室截面。全桥共计57节箱梁,箱梁边室外顶面设置节点板,纵桥向节点板中心距箱梁端头为2 m,桁梁斜腹杆用高强螺栓与箱梁节点板拼接。箱梁每隔3 m设置一道实腹横隔板,主梁横截面如图2所示(单位为m)。
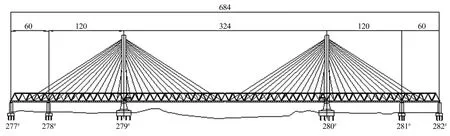
图1 裕溪河特大桥立面图
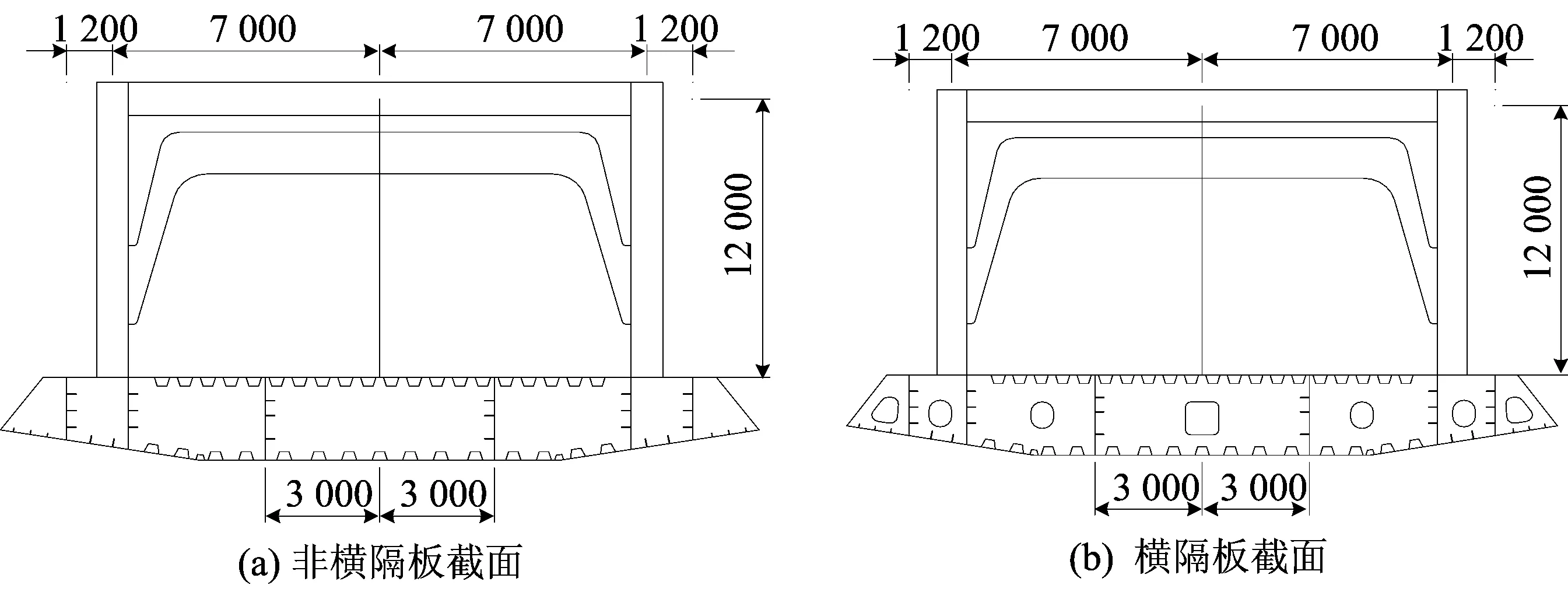
图2 主梁横截面
1.2 施工过程
主梁共计57个箱梁节段,其中两边跨采用顶推施工。该桥主塔离岸较远,在河床上建立了临时施工平台,导梁和前3节箱梁利用浮吊吊装到施工平台上拼接,之后安装桥面架梁吊机,对其余箱梁进行吊装悬拼。安装完成一段箱梁,向边跨顶推相应的距离。
箱梁施工示意图如图3所示。
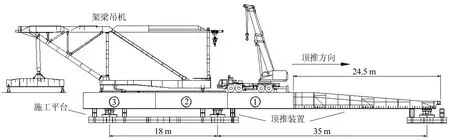
图3 箱梁顶推施工示意图
在安装4个箱梁节段后,桥面上已有足够的空间安装桁梁。已拼装完成4个箱梁节段,正在安装第1个节间桁梁的示意图如图4所示。图4中,粗实线为已经完成的主桁斜腹杆,虚线为拟安装的上弦杆,箱梁节点板在箱梁端部附近。安装主桁杆件时,导梁已经顶推上最近的临时墩。从箱梁① 、箱梁② 处开始安装桁梁,先用汽车吊将相邻的腹杆拼成2个三角形,再择机安装上弦杆。在④号梁处利用架梁吊机起吊并安装下一段箱梁,安装完毕后利用步履式顶推器向前顶推一段梁长的距离,完成一个循环作业。之后,重复以上安装步骤。
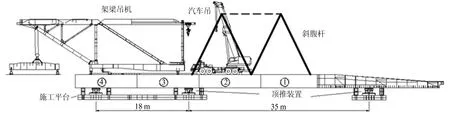
图4 箱桁同步施工示意图
上述整个施工过程就是裕溪河特大桥主梁采用的“箱桁同步施工”。
1.3 箱桁同步施工的关键问题
当上部桁梁能够安装时,箱梁已安装4个节段,并且前2段已经顶推到施工平台之外。在顶推过程中,主梁力学体系在悬臂或连续中交替出现,且悬臂长度或连续跨数的不同,使得钢箱梁的竖向受力变形也随之变化。桁梁安装时,先将相邻2个腹杆拼装成三角形,才能安装上弦杆。桁梁上弦杆对应节点距离将随着钢箱梁的变形而变化,因此保证上弦杆的顺利安装是箱桁同步施工的关键问题。
上弦杆安装变形示意图如图5所示。其中:粗实线为相邻2个腹杆拼装成的三角形点;C、D分别为斜腹杆交点;C、D之间细实线为正在安装的上弦杆。
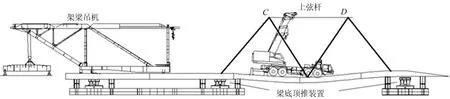
图5 上弦杆安装时箱梁变形示意图
下弦箱梁的变形会使斜腹杆产生转角和位移,使上弦节点C和D之间的距离l1与上弦杆设计长度l2不一致。上弦杆安装误差可用Δl=l1l2来表示。
在该桥中,螺栓孔要比螺栓杆直径大3 mm,若ΔL小于3 mm,则上弦杆可顺利安装;否则需利用顶推装置顶起箱梁或对斜腹杆施加外力等方法,强制调整上弦节点C、D之间的实际距离,辅助上弦杆件的安装。
但是,顶推器的调节高度有限、外力不便施加等因素使得这2种方法都只能作为安装的辅助措施。同时,强制安装将造成巨大初始应力,对桥梁的营运安全不利。
因此,在施工过程中,应尽可能使桁梁上弦杆安装偏差ΔL小于3 mm,以保证桁梁安装时的效率。
为此,本文通过对上弦杆安装距离偏差随施工阶段变化的分析,提出通过调整上弦杆的安装顺序,以实现无辅助措施的上弦杆安装。
2 上弦杆安装距离偏差的表达式
两节间相邻斜腹杆和对应箱梁变形前、后示意图如图6a、图6b所示。每段箱梁长度为L,梁段的中点分别为A、B,AC和BD为对应段箱梁的垂线,变形后A点、B点处的垂线与铅垂线夹角分别为α、β。
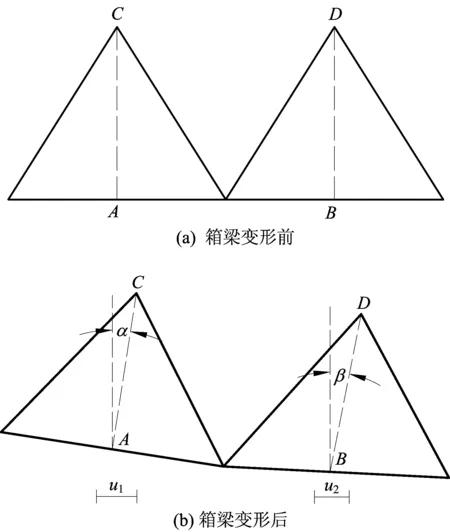
图6 钢箱梁变形示意图
箱梁变形后点C和点D之间的距离变化量分别为:
ΔL=ΔL1+ΔL2
(1)
ΔL1=(α-β)h
(2)
ΔL2=u2-u1
(3)
其中:ΔL为箱梁变形引起的上弦杆对应节间距变化量;ΔL1为箱梁截面转动引起的C、D距离的变化量,即箱梁弯曲变形产生的影响;ΔL2为箱梁AB的轴向变形所引起的C、D距离变化量;h为主桁的桁高,h=12 m;u1、u2分别为A、B处箱梁的轴向变形量。
箱梁截面相对转动和轴向变形引起的ΔL1和ΔL2可分别由(2)式、(3)式表示。(1)式ΔL相当于上文提到的Δl。
3 上弦杆安装距离偏差的过程模拟
3.1 有限元模型
为了获得在施工中上弦杆安装距离偏差,本文以将要安装第1根上弦杆的状态开始模拟,有限元建模思路以及施工过程如下:
(1) 第1根上弦杆开始安装时,箱梁已经顶推了4个节段。
(2) 每节箱梁和桁梁斜腹杆的安装设成一个施工工况,安装上弦杆、联结系和顶推设成一个工况。先安装箱梁、斜腹杆、上弦杆、联结系,再顶推,以此施工顺序建立有限元模型。
(3) 主桁杆件和箱梁拼装均为无应力拼装。
依据上述思路,用Midas/Civil有限元软件模拟该施工过程,主桁各杆件和下弦钢箱梁均采用空间梁单元模拟,假设已安装的桁梁和节点板无相对错动、完全耦合在一起,因此采用刚性连接模拟,模型按照累加进行计算,即每一个施工阶段的结果都是前面所有施工阶段影响的累加[12]。
箱桁同步施工模型如图7所示。该模型为第1根上弦杆已经施工完成,将要安装第2根上弦杆。
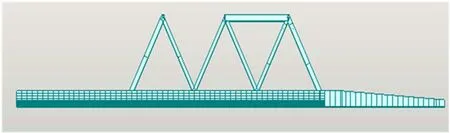
图7 箱桁同步施工的有限元模型
通过增加箱梁节段数量、安装桁梁、向前顶推等建立同步顶推模型,模型共35个工况,见表1所列。

表1 有限元施工工况
工况1为已经顶推完4节箱梁,并安装完成第1根上弦杆所对应斜腹杆,此时测量第1根上弦杆的安装距离偏差;工况2为安装第1根上弦杆和箱梁5后顶推完成;工况3为已安装第2根上弦杆对应斜腹杆和箱梁6,此时测量第2根上弦杆的安装距离偏差(图7);工况4为安装第1根上弦杆和箱梁5后顶推完成,等等。
同时,为了研究汽车吊对上弦杆安装距离的影响,建立汽车吊单独作用模型。汽车吊施工时不可能总在一个理想位置,因此需研究汽车吊在不同位置施工对上弦杆安装距离的影响。模型中已安装的构件没有重量,只有刚度,在上弦杆对应斜腹杆范围内布置汽车吊移动荷载,以计算汽车荷载对上弦杆安装间距的影响。
3.2 有限元结果
通过有限元计算,可得汽车吊对各个上弦杆安装间距的影响值,本文仅列出汽车吊对第1根上弦杆安装距离的影响曲线,如图8所示。其中:横轴表示汽车吊作业时的位置,在施工范围内以距施工平台最近的位置为零点,导梁方向为正方向;纵轴表示汽车吊荷载对第1根上弦杆安装距离的影响值。
由图8可知,汽车吊对第1根上弦杆安装距离的影响最大值为-1.28 mm,汽车吊荷载的影响不能够忽略。设不考虑汽车吊的上弦杆安装距离偏差为X,汽车吊对上弦杆安装距离影响值为Y,当Y使|X+Y|能够取得最大值时,汽车吊的影响最不利,则将此Y值计入上弦杆安装距离偏差。
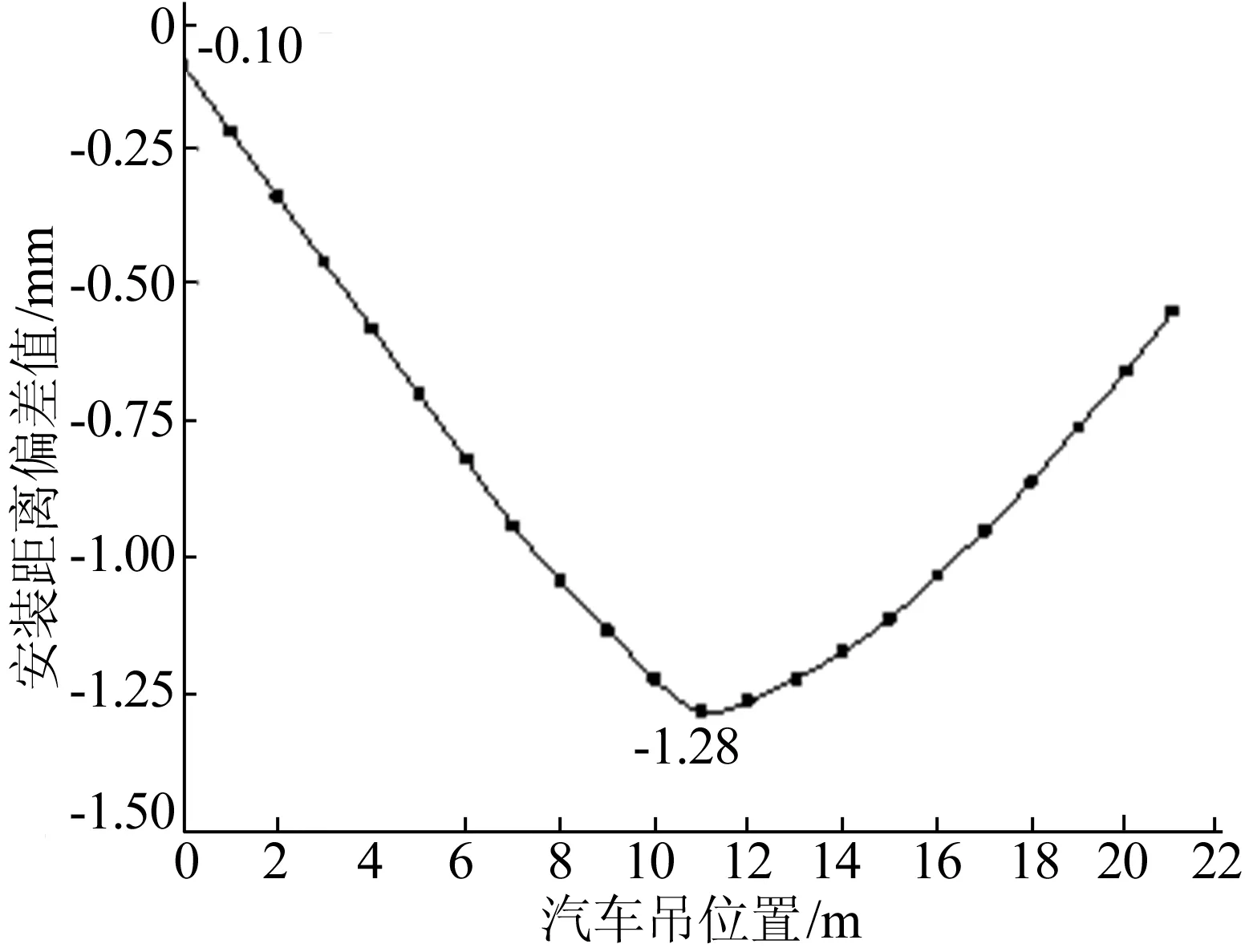
图8 汽车吊对第1上弦杆安装距离的影响曲线
已安装4个箱梁节段后开始安装桁梁,顶推过程中上弦杆安装距离偏差见表2所列。
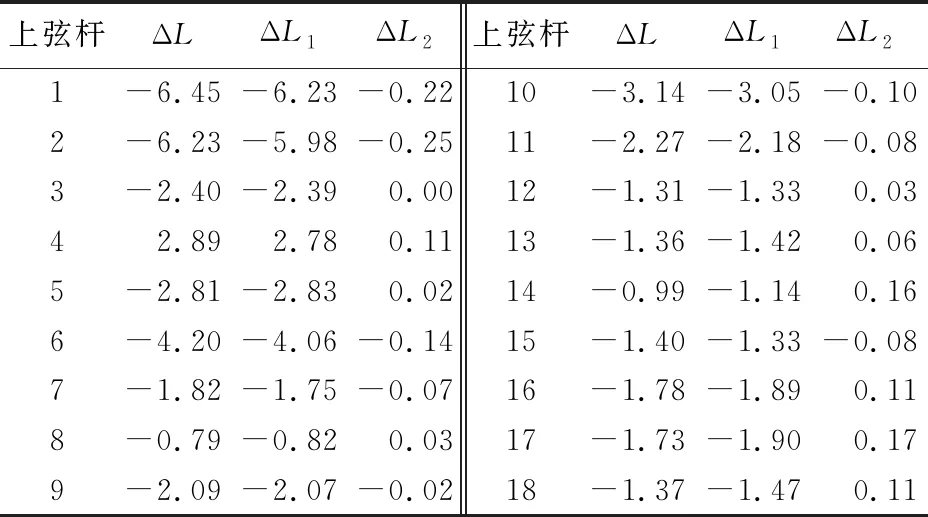
表2 上弦杆安装距离偏差 mm
从表2可以看出,ΔL和ΔL1比较接近,这说明上弦杆安装距离偏差主要是由箱梁的截面相对转动所引起的。随着梁段向前顶推以及支撑临时墩的增多,施工区域箱梁的相对转动逐渐减小,上弦杆安装距离偏差也在逐渐减小。
3.3 改变上弦杆安装时间
为了研究在不同顶推阶段开始安装桁梁对上弦杆安装距离的影响,分别建立顶推5、6个箱梁节段后开始安装上弦杆的有限元模型,其他条件与4个箱梁节段开始安装桁梁相同。
已安装4、5、6个箱梁节段后再开始安装桁梁的情况下,第1~18根上弦杆的安装距离偏差为ΔL,如图9所示。
从图9可以看出,在4个箱梁节段后开始安装桁梁的施工方法中,第1、第2和第6根上弦杆安装距离的偏差较大,分别为-6.45、-6.23、-4.20 mm,超出了施工允许值。在安装前4根上弦杆时,ΔL变化幅度比较大,这是因为此时处在顶推初期,导梁受到的支反力、箱梁的弯矩在快速变化。从第7根上弦杆起,安装间距偏差ΔL大部分都在3 mm内,杆件易于安装,说明箱桁同步施工方法是可行的。随着顶推施工的进行,上弦杆的安装距离偏差也在逐渐减小,但第1、第2、第6根上弦杆安装距离偏差较大,不符合安装误差要求,需要进行调整。安装5个箱梁节段后再安装桁梁,除了第1、第2根上弦杆安装间距偏差比较大,不符合安装要求,其余上弦杆安装顺利。安装6个箱梁节段后再安装桁梁,第1、第2、第4、第16根上弦杆安装不符合要求。
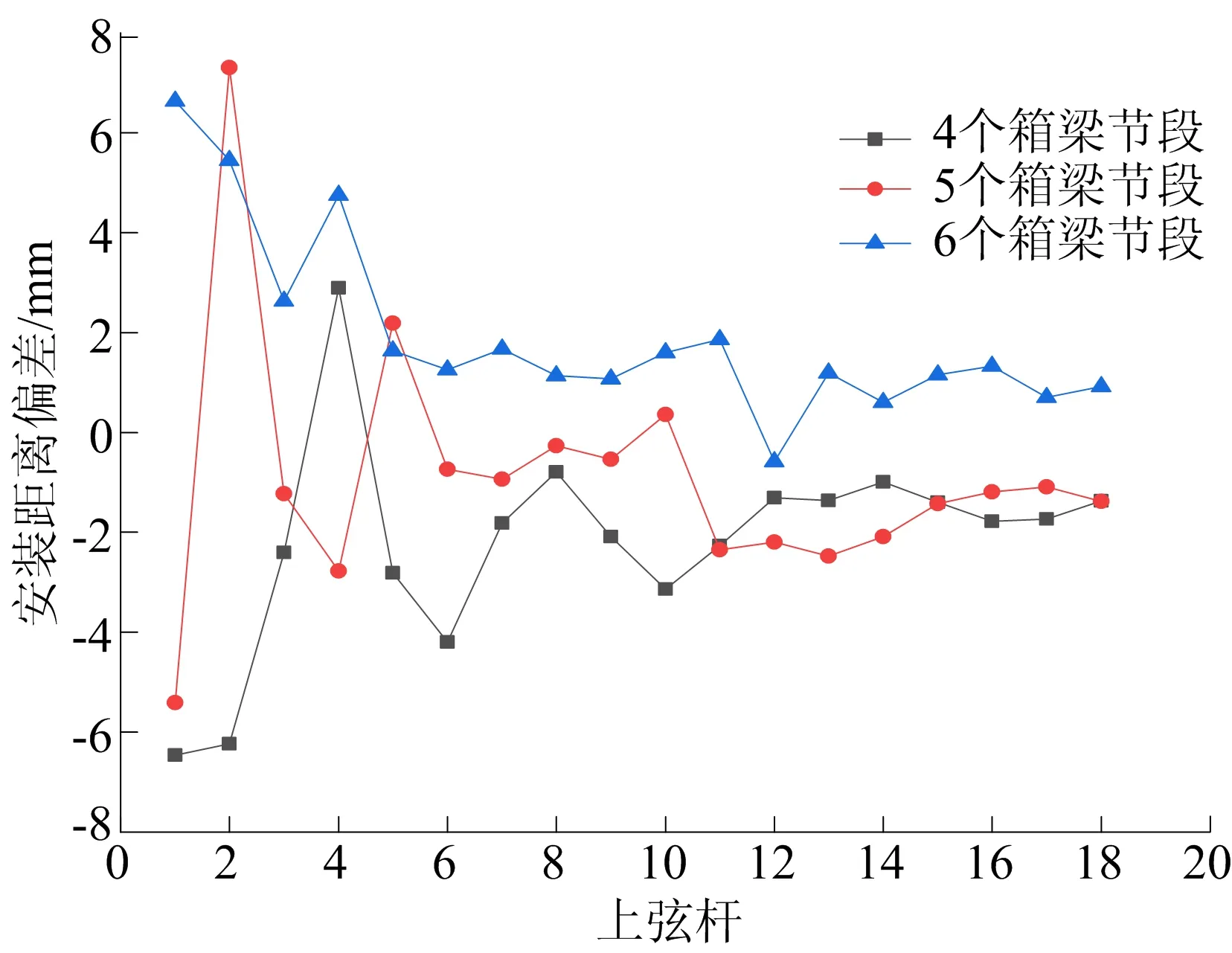
图9 上弦杆安装距离偏差
4 改进的桁架拼装方案
图9中,随着顶推施工的进行,主梁长度在增加,但主梁获得的支撑也在增加,上弦杆安装距离偏差有逐渐减小的趋势,因此考虑在原施工流程的基础上进行改进,考虑不安装前面若干根上弦杆,而先安装之后的上弦杆,等到施工区域主梁处在合适状态再安装前面空缺的上弦杆,即调整上弦杆的安装顺序。经过模拟对比发现,在顶推6个箱梁节段后开始施工桁梁的基础上改进能取得较好效果。
具体方法为:当4、5节箱梁节段安装顶推到位时,将桁梁第1、2节间的斜杆拼成三角形,暂不安装上弦杆;6节箱梁节段安装顶推到位后,先安装第2根上弦杆;第7节箱梁顶推到位后同时安装第1、3根上弦杆;之后按照一节箱梁一节桁梁的方法进行施工。依上述过程建立有限元模型,计算得出上弦杆的安装距离偏差ΔL。
改进后的上弦杆安装距离偏差如图10所示。按改进后的桁架施工,上弦杆安装距离偏差值ΔL使上弦杆1、2、6均能够顺利安装,所有误差均在螺栓允许安装误差3 mm以内。
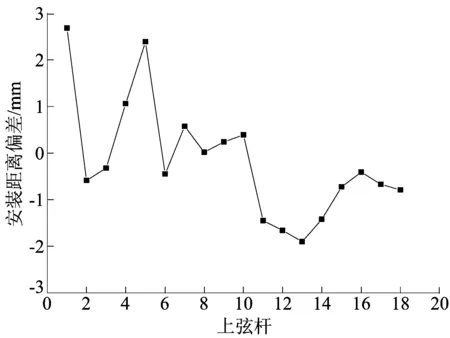
图10 改进后的上弦杆安装距离偏差
因此,该方法理论上能够实现箱桁同步施工,通过调整上弦杆的安装顺序,实现了无辅助措施的上弦杆安装。
在改进的施工方法中,先安装桁梁前3节斜腹杆,暂不安装上弦杆,第6节箱梁顶推后,顶推至施工平台外的梁长在第1临时墩两侧相对接近,桁梁第2节间对应箱梁弯曲变形较小,使得第2根上弦杆距离偏差较小;第7节箱梁顶推到位后,桁梁第2节间刚好处在临时墩上方,第1、第3节间斜腹杆在跨中位置,箱梁弯曲造成斜腹杆转动较小,上弦杆容易安装。因此,找到顶推中箱梁比较平衡的状态是同步顶推施工的关键。
5 改进拼装方法的实施效果
在裕溪河桥箱桁同步施工过程中,上弦杆安装均满足桁架杆件的施工要求。理论计算和实际施工中上弦杆安装距离偏差的对比如图11所示。由图11可知,实际施工中上弦杆安装偏差均小于3 mm。
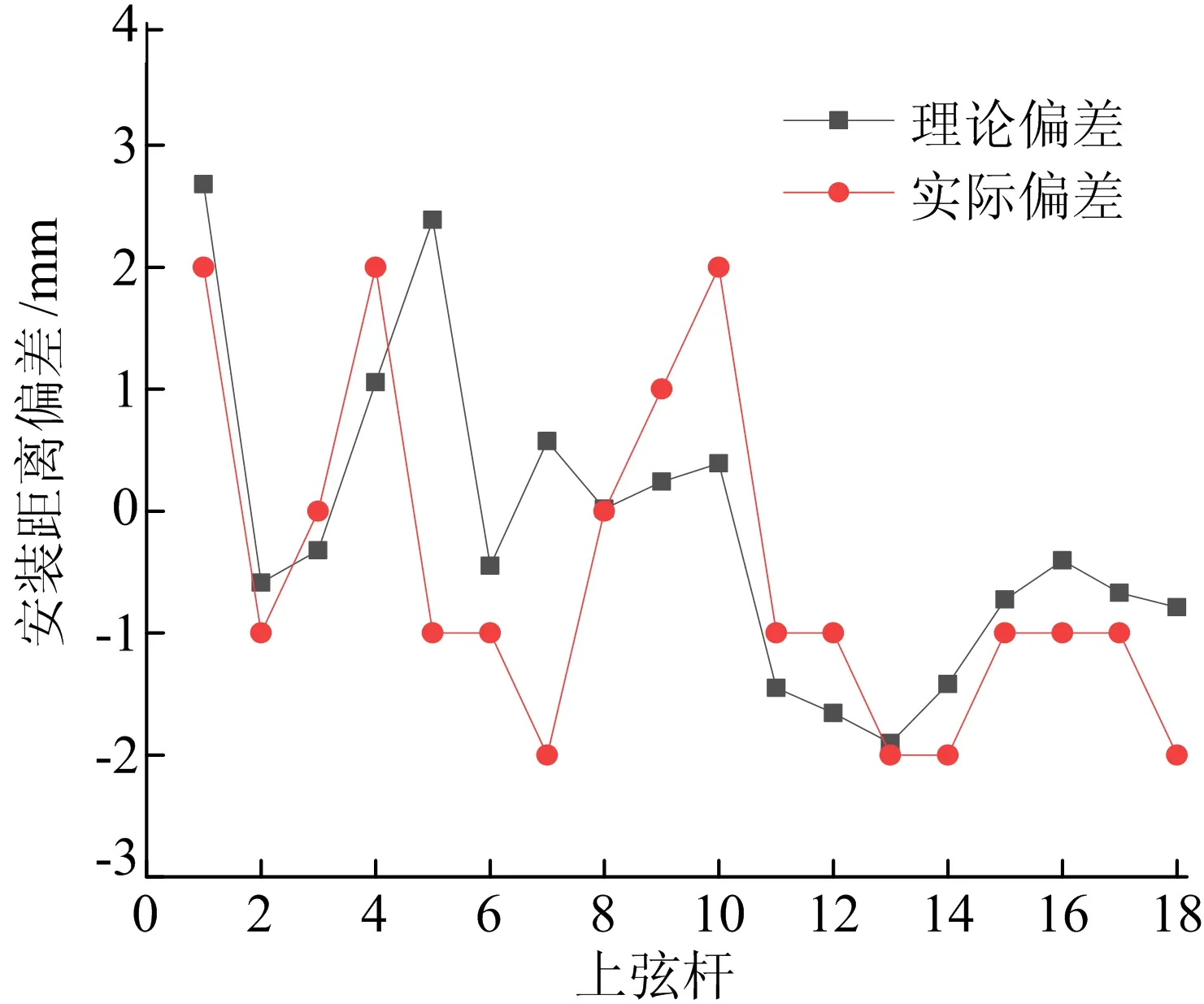
图11 上弦杆安装距离偏差理论值与实际值对比
部分上弦杆的理论和实际偏差差值较大,由于施工材料堆放、箱梁安装偏差等多种因素,导致实际施工和模型存在一定的误差,但是2条曲线整体吻合效果较好,证明利用改进拼装方法能够将偏差控制在螺栓孔可调范围内,实现了上弦杆的顺利安装。
6 结 论
通过本文分析得出以下结论:
(1) 汽车吊荷载对本桥第1根上弦杆安装距离影响可达-1.28 mm,在上弦杆安装偏差分析中应考虑汽车吊荷载的影响。
(2) 调整上弦杆开始安装时间、顺序,找到箱梁在临时墩两侧相对平衡状态是同步施工的关键,平衡时箱梁弯曲变形较小,上弦杆安装距离偏差较小。
本文施工顺序为6节箱梁时安装第2根上弦杆,7节箱梁时安装第1、3根上弦杆。箱桁同步施工既可提高施工效率,又可减小辅助措施带来的初应力,该施工方法为同类型桥梁施工提供了一定的经验。
