基于回归分析的COVID-19 死亡率影响因素分析

2021-06-01李庆禧贾云涛林俊锋罗星怡

科技与创新 2021年10期

关键词：回归方程残差气压

李庆禧，贾云涛，林俊锋，罗星怡

（北京理工大学珠海学院数理与土木工程学院，广东珠海519088）

1 引言

1.1 研究背景

1.2 研究目的

研究目的为填补国内外新冠肺炎（COVID-19）疫情死亡率与天气因素研究的空白，帮助决策者做出正确的决策，减少新冠肺炎的死亡人数，在实现人道主义的同时减少资源的浪费。

1.3 研究思路

首先确定了有关天气的几项关键因素，如气压、湿度与温度等。接着，为了减少不同医疗条件、不同防疫政策带来的差别，选择搜集同一时间段内、同一地区的各个因素的具体数据与对应的新冠肺炎死亡率。紧接着为了避免因为数据量纲不同带来的差距，对因变量进行标准化，接着进行回归分析，在分析中，需要判断回归方程是否存在违背基本假设的情况，最后根据回归方程确定影响脑卒中发病的关键天气因素。研究思路如图1 所示。

2 数据采集与整理

2.1 数据来源

本文数据为2020-01—2020-04 美国疫情较为严重的27个州的数据，其中天气数据为该时间段中各因素的平均数据，死亡率为该时间段的死亡率。数据主要来源于Kaggle 竞赛平台。数据结构包含八项天气数据（平均气温、平均站压、平均气压、相对湿度、平均露水、平均风速、总降水量、昼夜温差）和新冠肺炎死亡率。

2.2 数据预处理

不同因素之间的量纲水平并不相同，这种差别会给后续研究带来一定的影响。为了消除这种影响，对数据进行无量纲化的处理。

图1 研究思路图

2.3 数据可视化

数据可视化如图2 所示。

图2 数据可视化

根据图2，可以得出新型冠状病毒死亡率在美国有从南到北递增的趋势。

3 回归分析

3.1 相关系数

为了确定天气因素与死亡率之间是否存在关系，首先求解平均气温、平均站压等天气因素与死亡人数的偏相关系数，并对偏相关系数进行显著性检验。得到结果如图3 所示，可以发现有部分因素与死亡人数有显性的相互关系。但在多元变量的情况下，两个变量之间的关系还可能受到其他因素的影响，因此我们进行回归分析，进行下一步探讨。

图3 相关系数检验表

3.2 逐步回归分析

在确定了各因变量与自变量之间有一定关系后，可以利用R 语言建立回归模型。但为了排除无关变量的影响，同时保留关键变量，进行逐步回归。得到的方程结果如下：

模型方差分析如表1、表2 所示。

丛书选题契合“五位一体”总体布局和“四个全面”战略布局。各卷撰写过程中，正值党的十九大召开，各卷作者深入学习十九大报告，内容叙述有了更新。主编还适时调整选题，特别增设生态文明卷，直接呼应了党的十九大明确把“坚持人与自然和谐共生”作为新时代中国特色社会主义的基本方略之一的重要精神。如此，各卷记述内容也力求用习近平新时代中国特色社会主义思想印证和观照我国改革开放40年的历史发展。

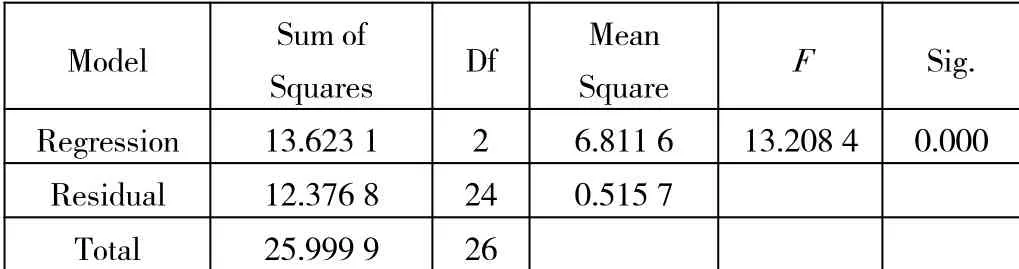
表1 模型方差分析表1

表2 模型方差分析表2

3.3 显著性检验

得到方程后，进行显著性检验。首先进行回归方程的显著性检验，从方差分析表可以得到，大部分的误差来自回归方程，即回归模型造成的误差。将回归平方和的均方误差和残差平方和的均方误差构造F统计量，进行F检验，求得F统计量为13.208 4，大于检验统计量2.494，拒绝原假设，证明死亡率与各天气因素有显著的线性关系，即回归方程是显著的。

接着进行回归系数的显著性检验，利用R 语言计算每个回归系数的t统计量，并进行t检验。得到平均气压和相对湿度都是显著的，即对死亡率有显著的影响情况。

3.4 拟合优度检验

得到回归模型后，进行拟合优度检验。从方差分析表中得到回归方程的样本决定系数R2=0.524 4，复相关系数R=0.724 2。考虑到样本容量与自变量的个数，可以接受这样的回归效果。同时，在自变量个数为2，自由度为27，显著性水平为0.05 的条件下，检验的系数为0.446。复相关系数远大于检验系数，因此可以认为方程具有较好的拟合效果。

3.5 有效性检验

为了判断方程是否存在违背马尔科夫基本假设的情况，使用R 语言分别针对三种情况进行检验。首先是多重共线性的情况，用扩大因子法，得到VIF值如表3 所示。

表3 各系数VIF 值

可以看出各自变量的VIF值明显小于10，即没有存在的多重共线性。接着用特征根判定法，得到x6与x7的特征根都显然大于0，最后再用条件数法，得到Kappa值等于1.390 647，小于100，认为设计矩阵X没有多重共线性。

接着进行自相关性的检验，进行DW 检验，得到方程的DW 值为1.34，P值等于0.27，大于显著性水平0.05，因此认为残差不存在自相关。

最后进行异方差检验，利用R 语言ncvTest 函数进行检验，得到对应P值等于0.514 46，大于显著性水平0.05，即不存在异方差，因此认为方程不存在违背马尔可夫基本假设的情况。

3.6 残差分析

残差分析图如图4所示。从图4看出残差基本在直线e=0附近随机变化，并在变化幅度不大的一个区域内，显然残差和估计值基本是无关的。从Normal Q-Q 图中发现残差基本符合正态分布，因此模型没有出现违背基本假设的情况。然后看到Scale-Location 图，发现方差基本是一个常数，也可同样判断残差和估计值基本是无关的。从Residuals VS Leverage 图中可以检查数据中是否有特别极端的点。这里发现共有两个数据的Cook 距离大于0.5，可以判定为异常值，因此在后续中，需要着重讨论这两个异常值。

4 结论与推广

4.1 结论

在得到有效的回归方程后，可以对方程结果进行解释。在四个变量中，只有平均气压（Slp）与相对湿度（Rh）通过了t检验，因此主要对这两个因素进行分析。平均气压的回归系数为负，说明新冠肺炎的死亡率与平均气压呈负相关。从现实的角度看，气压对人体生理方面的影响主要是人体内氧气的供应，气压低时，人体容易出现头晕、头痛、恶心、呕吐和无力等症状，神经系统也会发生障碍，甚至会发生肺水肿和昏迷等症状，而新冠肺炎的症状中，绝大多数患者死于呼吸衰竭，即因为肺里有大量的黏液，氧气无法进入肺泡进行气体交换，导致窒息而死。因此，有一定理由相信气压会影响新冠肺炎的死亡率。其中，气压越低，死亡率越高；气压越高，死亡率越低。

图4 残差分析图

相对湿度的系数为负，说明新冠肺炎的死亡率与平均气压呈负相关。空气中的相对湿度主要影响人们的舒适感，在较高的相对湿度中，容易使人烦燥、疲倦、食欲不振，较低的相对湿度，易引起上呼吸道粘膜感染。对于新冠肺炎，典型症状包括咽痛鼻塞等上呼吸道感染症状。同时，新冠肺炎最初爆发在武汉时，也是在天气较为寒冷、湿度较小的季节。因此有一定理由相信相对湿度会影响新冠肺炎的死亡率。其中，湿度越大，死亡率越低；湿度越小，死亡率越高。