基于土壤墒情自动监测与人工数据对比分析及解决方案探析
2021-05-31王丹丹
王丹丹
(辽宁省盘锦水文局, 辽宁 盘锦 124010)
1 概述
抗旱的重要基础工作在于对土壤墒情的监测,旱情最为主直接表征的指标即为土壤含水量[1]。近些年来,按照国家防汛抗旱指挥部办公室公布的土壤墒情检测合格名录各省份开始安装自动墒情监测站点[2]。辽宁省已初步建成墒情自动监测站85处,但从自动墒情监测站总体运行情况看,其土含观测数据和人工观测数据存在一定的误差,精度及可靠程度不高,很多站点的土含观测数据不能用于区域旱情监测分析[3]。很多研究学者针对自动墒情监测站误差原因进行剖析,其最为主要的原因在于自动墒情监测站一般安装在无耕作措施的土壤围栏内,很难对大田真实含水量进行有效测定,需要通过建立自动墒情站监测土壤含水量和人工实测的大田含水量之间的回归方程,对其测定的误差进行校准分析,从而提高自动墒情监测站的土含测定精度[4]。当前,对于自动墒情监测站误差校准得到学者的关注和研究,
哈建强[5]以沧州地区为例,对区域土壤墒情时间变化规律进行研究,对不同作物方式下的土壤墒情监测规律进行了系统分析。杨威[6]对辽宁省自动墒情监测站数据误差成因及解决方法进行了探讨,提出了减小自动墒情监测站环境和人工墒情监测等误差的方法。王德维[7]土壤墒情自动监测与人工烘干法进行比测研究,分析结果表明机测的含水量与土壤实际含水量相关性很好。马尚贤[8]采用"人工造墒"的方式对自动墒情监测仪器公式进行标定,结果表明30组比测数据绝对误差均小于±4%,达到规范规定要求。祖佳[9]对土壤墒情自动测报系统进行分析,表明壤墒情自动测报系统将是未来墒情观测的发展方向。邓超[10]介绍了土壤墒情自动监测系统比测方法,通过比测表明数据合格率为85.7%,大于80%的要求。以上研究表明土壤墒情自动监测是未来墒情监测的趋势和发展方向,但需要通过比测方法对自动墒情监测站观测误差进行校准[11]。近些年来,铁岭地区已经布设一批土壤墒情自动监测站,显著提高了区域墒情观测的自动化水平,但在实际应用,土含自动观测的精度还难以满足标准要求,为提高铁岭地区墒情观测精度,本文以铁岭王宝庆自动墒情站点为实例,对其墒情自动观测误差进行校准分析[12],研究成果对于铁岭其他站点误差校准具有参考价值。
2 误差校准方法
对自动墒情监测站观测的土壤含水量数据和人工观测数据进行回归分析,并基于最小二乘方法建立回归方程:
θv=av2+bv+c
(1)
式中θv为墒情自动观测站监测的土壤含水率,%;v为探针电压输出值,V;a,b,c为回归系数。结合建立的回归方程,对土壤墒情自动监测数据进行误差校准,当校准的误差值低于±5%,认定满足墒情观测的标准要求,误差计算方程为:
(2)
式中xi为自动墒情站采集的不同深度(20 cm、30 cm)的土壤含水率,%;ai为比测分析中同一深度下人工采集分的土壤含水率,%;N为对比观测数据采集的次数。
3 实例应用
3.1 比测分析方法
在野外进行比测观测试验时,采样环刀等设备对王宝庆站土壤墒情监测站点原状土进行现场采集,土样孔隙度要与土壤样品保持一致,土壤样品在实验室浸泡饱和后进行晾晒,土壤含水率由高逐步向低递减或者采集含水量不同的样本,对不同含水量下土壤样本的监测信号进行测定,同步采用人工烘焙方法对采集的土样进行含水量的称重。对于监测设备不能直接查看信号,需要将仪器观测的土壤水数据进行公式转换成对应的信号数值,现场率定时需要对不同信号下采集的土壤含水量状态以及对应的土壤含水量在一次较大降水后进行比测分析,若降水量不够满足试验条件,则可以采用人工浸泡方式对土壤饱和状态下自动监测站观测的信号数值进行分析。
在进行比测分析时,观测试验组数一般不低于10组,观测的数据点需要均匀分布在率定曲线上,覆盖含水量的高低变化过程。误差分析的采集数据需要良好的代表性和可靠度。率定曲线和数据点偏离度需要合理范围内。可以剔除偏离度较大的数据异常点,不能增加数据值为0的点进行分析。在采样时需要采用环刀对不同深度的2~3个土壤样本进行采集,对不同土壤容重进行均值计算,作为试验土壤的容重均值,该指标的准确度对误差率定曲线具有较大程度影响,土壤容重应采用人工烘焙方法进行精准测定。将对应深度下含水量测定数据和干容重进行折算得到含水量体积,再同监测信号进行误差率定。率定的公式需要在1~2 a后与人工烘干方法进行比测分析,若比测偏差较大则需要重新率定,对原率定公式进行替换。
3.2 比测数据相关性分析
对铁岭王宝庆自动墒情站的误差率定曲线进行分析,在进行体积含水量转换后,结合人工烘焙方式下的土壤含水量数据进行相关性分析,不同深度(20 cm、30 cm)比测数据相关分析结果见表1。

表1 人工烘焙方法和土壤墒情观测分析不同深度含水量相关性分析结果
从相关性分析结果可看出,随着取土深度的增加,比测分析下人工观测的土壤含水量和自动观测的土壤含水量相关系数逐步减小,相比于土壤含水量瞬时值,采用日均值处理后由于均化效应,使得其比测相关性提高。此外不同深度下比测相关系数高于同一深度下的相关系数, 可见深度对于比测含水量相关度影响程度较低。
3.3 比测误差分析
在相关性分析的基础上,统计分析不同深度下比测误差(见表2)。

表2 不同深度土壤含水量比测误差分析结果 %
比测误差随着深度增加而逐步递增,采用均化处理后的土壤含水量比测误差有所降低,相比于均化处理前,20 cm和30 cm深度下比测误差降低超过9%。此外从各深度比测误差分布可看出,2种深度下的比测存在一定的系统误差。
3.4 误差率定曲线
结合最小二乘原理对各深度下的误差率定回归方程进行分析,各深度下误差率定回归方程为:
20 cm深度下:
y=-1.024 8x+23.289
(3)
30 cm深度下:
y=-0.483 2x+16.824
(4)
在误差率定方程中x和y分别为自动监测站观测含水量和修正后的含水量。结合2个深度下的误差率定曲线可以对铁岭宝庆自动墒情站点的土壤墒情进行误差校准,铁岭其他自动墒情监测站点也可结合该方法进行误差校准。
3.5 率定公式精度对比
各误差率定方程的回归次数可直接影响土壤墒情自动监测站的误差校准精度,为此本文对不同率定方程的精度进行对比分析(见表3)。
随着回归次数的增加误差逐步递减,铁岭地区适合采用一元三次方程进行误差率定回归方程的建立,但考虑增加回归方程的次数,则对样本数据系列的长度要求也将增加。因此在进行比测分析初始阶段,建议采用一元一次方程进行误差率定回归方程的建立,随着比测分析数据的逐步增多,可以通过转换误差率定方程的回归次数,提高自动墒情站点土壤含水量的监测精度。
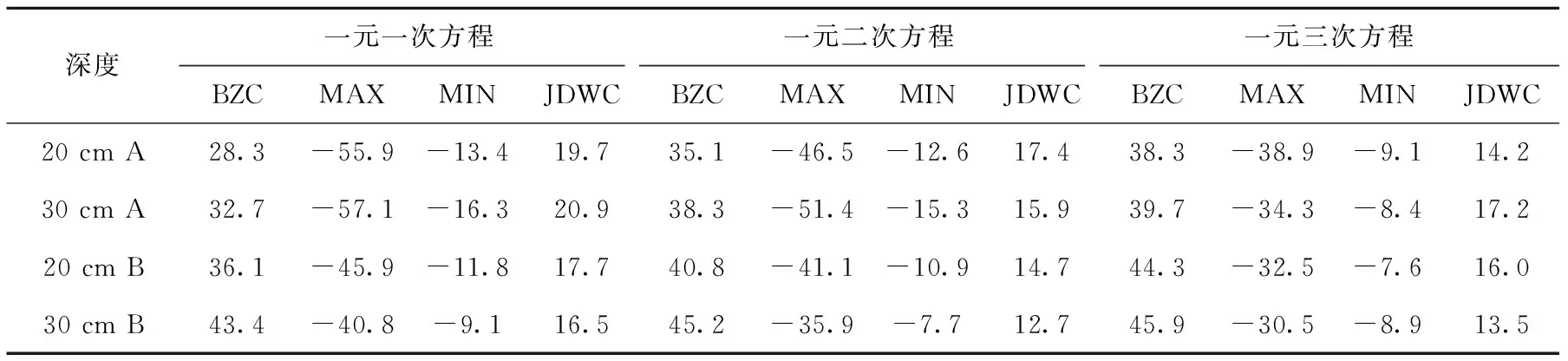
表3 回归方程次数对误差率定精度影响分析结果
4 常见问题解决方案
本文对误差修订回归方程建立的常见问题进行解决方案的分析,具体解决方案分别为:
1)在墒情站点建设初期,由于比测分析的数据较少,误差修订方程很难建立,因此,可通过日均值方法对比测分析的土壤含水量进行处理,对不同深度下误差进行校准,可实现土壤含水量观测精度的提高;
2)误差率定回归方程需要大量的比测分析数据作为支撑,由于站点运行初期比测分析数据量较少,很难满足墒情观测的标准精度要求,因此,可采用相邻站点的土壤墒情自动监测数据进行比测分析,实现墒情监测数据的动态误差校准,从而满足不同阶段的土壤墒情监测站点的误差标准要求。
5 结语
1)在王宝庆自动墒情监测站运行初期,可采用日均处理方式实现其误差精度的改善,通过比测分析,采用日均处理方式下,不同观测深度下比测相关系数均可提高0.15以上;
2)通过误差率定方程可实现土壤墒情自动监测站的误差校准,通过1个站点的误差率定方程的建立,也可用于其相邻站点的墒情自动监测的误差校准,从而解决类似站点建设初期由于比测数据较少精度难以满足标准要求的难题。
