双牌水库在汛期优化调度运行研究

2021-05-31杨博石张贵金

湖南水利水电 2021年2期

杨博石，张贵金

（长沙理工大学水利工程学院，湖南长沙410114）

1 工程背景

双牌水库根据工程的开发任务和规模等，考虑大坝自身和下游防洪安全，采用天然河道年最大洪水系列数据，通过经验频率计算得到设计洪水，通过水库调洪计算得到水库防洪和调节库容及其特征水位。在设计的各个环节都偏于安全保守考虑，导致设计洪水值普遍偏大[1]，另一方面，由于多种原因，多数水库在汛期实际调度运行时，为了保证大坝安全及下游防洪安全，又进一步降低了汛限水位，减小了水资源利用效率[2～3]。

洪水漫顶风险分析计算对于水库大坝安全运行和大坝风险管理具有重要意义，方法有直接积分法、结构可靠度分析法、抽样模拟分析法等，在工程实践中，数据的可用性、模型的复杂性和结果的精度要求是分析方法选取的重要依据[4]。对漫顶风险影响最大的是洪水的不确定性，关于洪水分析计算，单变量经验频率分析是传统水库洪水计算的常用计算方法，目前研究较多的是洪峰、洪量、洪水过程线形状等多变量分析方法[4～7]。

本文采用Copula-Monte Carlo法构建入库洪峰和洪量的联合分布模型及漫顶风险计算模型，并量化了不同起调水位下的漫顶风险，探索了提高水库水资源利用效率及优化调度运行的方法，为相关研究提供了应用案例。

2 基于Monte Carlo的大坝洪水漫顶风险计算模型

2.1 大坝漫顶风险分析模型

洪水漫顶风险率pFO是指坝前最高洪水位Hmax超过坝顶高程hc的概率，计算公式如下[8]：

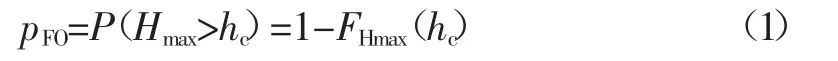
式中FHmax（hc）——Hmax的概率分布函数。

可以看出，得到FHmax（hmax）是计算洪水漫顶风险率的关键问题。本文将采用Copula-Monte Carlo法来模拟洪水峰量联合分布和求解pFO。

2.2 洪峰和洪量的联合分布

假设设计洪水洪峰和洪量的边缘分布分别为u=FQ（q）、v=FW（w）。根据Sklar定理，参考刘章君等人的计算方法[4]，用一个二维Copula函数C建立Q和W的联合分布函数：

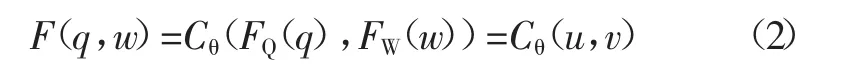
式中Q、W——分别为洪峰和洪量；

q、w——分别为Q、W对应的取值；

F（q，w）——Q和W的联合分布函数；

θ——Copula函数的参数。

选用Gumbel、Clayton、Frank三种两变量Archimedean Copula函数作为备选函数，其基本形式、参数θ及θ与Kendall’sτ之间的关系如表1所示。采用Kolmogorov-Smirnov（K-S）检验进行边缘分布模型的检验；对Copula函数拟合优劣进行评价的方法有均方根差（RMSE）、K-S法、AIC准则法和Bias值等；K-S值通过检验，RMSE、AIC和Bias值越小，表示Copula函数的拟合程度越好。

当洪峰Q为指定值q时，通过建立的洪峰洪量联合分布Cθ（u，v），可以得到洪量W的条件分布，其数学表达式为[4]：

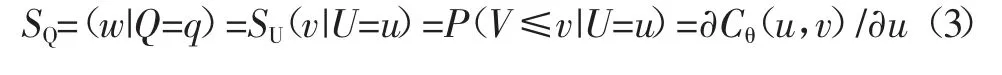
表1 三种备选两变量Copula函数基本形式、参数θ及θ与Kendall’sτ的关系[4,9～10]

2.3 漫顶风险计算

采用Copula-Monte Carlo法计算洪水漫顶风险率pFO，具体步骤如下：

1）生成两个服从[0，1]均匀分布的独立随机数r1和r2。

2）令u=r1，SU（v|U=u）=r2。

3）求解SU（v|U=u）=r2，得到：v=SU-1（r2|U=u）。

4）计算q=FQ-1（u），w=FW-1（v）得到一对随机洪峰洪量组合（q，w）。

5）选取典型洪水过程线，采用变倍比放大方法[5]来计算设计洪水过程线：

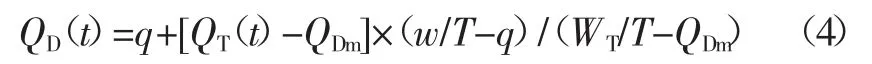
式中QD（t）——设计过程在t时刻的流量；

QT（t）——典型洪水过程在t时刻的流量；

WT——典型洪水历时T内的洪量；

QDm——典型洪水的洪峰流量；

q、w——分别为步骤4）中所求得的洪峰洪量。

6）结合步骤5）中所求得的设计洪水过程线QD（t）、水库泄流曲线和库容曲线，按汛期调度运行方式进行调洪演算，得到坝前最高水位hmax。

7）重复步骤1～6共n次，可以模拟出n个hmax，通过数学期望公式计算经验频率曲线，得到Hmax的概率分布函数FHmax（hmax）。

8）计算洪水漫顶风险率pFO=1-FHmax（hc）。

3 双牌水库漫顶风险分析

3.1 洪峰洪量分布的确定

参照《水利水电工程设计规范》（SL-2006），选用双牌水库坝址处水文站1959—2019年实测2 h流量数据，提取双牌水库的年最大洪峰流量Q和3日洪量W系列数据，进行经验频率计算。采用P-Ⅲ分布作为边缘分布建立洪峰与洪量的联合分布，分析洪水漫顶风险。

采用K-S检验法对P-Ⅲ函数的矩法估计参数进行假设检验，由表2可知洪峰和洪量系列的K-S值均低于临界值为0.246，通过K-S检验。

为了选定拟合效果最优的Copula函数，采用表1中的三种常用Copula函数建立双牌水库Q和W之间的二维联合分布，利用Kendall相关系数τ估计其参数，采用2.2中所提及的方法对Copula函数模型进行检验和拟合优度评价，结果见表3。结果表明三种备选Copula函数K-S值均小于临界值0.246，通过K-S检验；其中，Gumbel Copula函数的RMSE、AIC和Bias值最小，为拟合度最优的Copula函数。由图2可以看出经验频率值与理论频率值的拟合情况较好，表明采用Gumbel Copula函数所建立的联合分布是合理可行的。

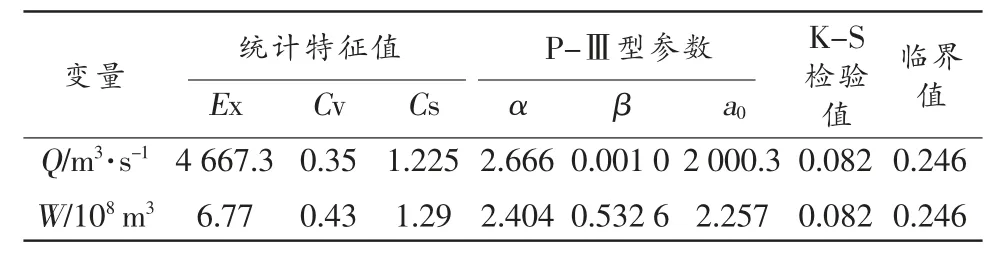
表2 涔天河水库洪水统计特征值和P-Ⅲ型分布参数估计结果

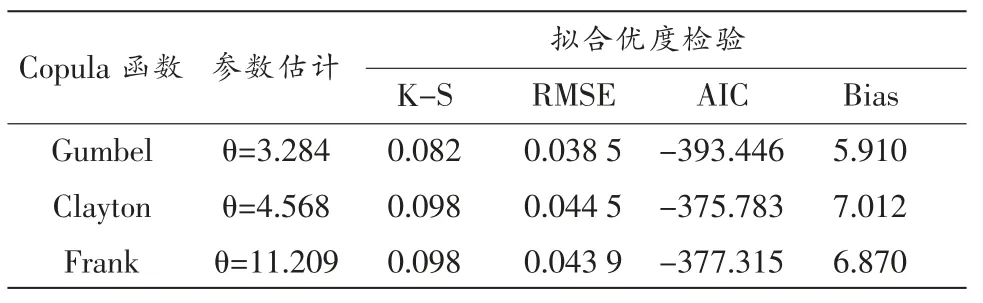
表3 Copula函数的参数估计和拟合优度检验值结果

3.2 洪水漫顶风险计算结果

按2.3节中的方法步骤，利用3.1中拟合度最优的Coupla函数（Gumbel Copula函数）建立的条件分布，对比随机生成10万组洪峰、洪量组合与实测值的情况如图3所示，表明Gumbel Copula函数能够较好地捕捉洪峰、洪量的相关性结构。

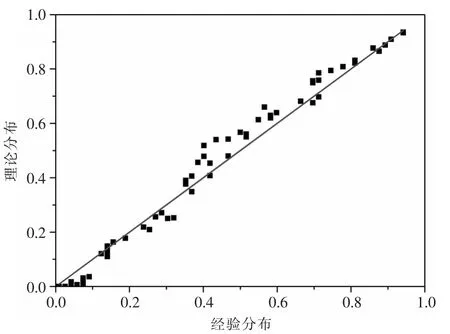
图2 联合观测值的经验分布和理论分布比较

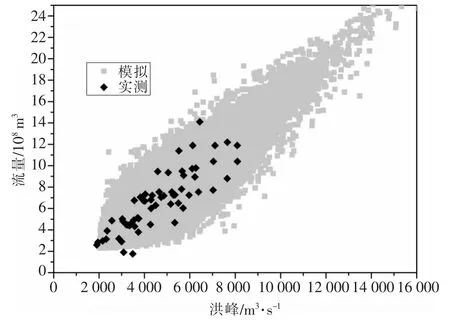
图3 随机模拟和实测的洪峰、洪量点据比较

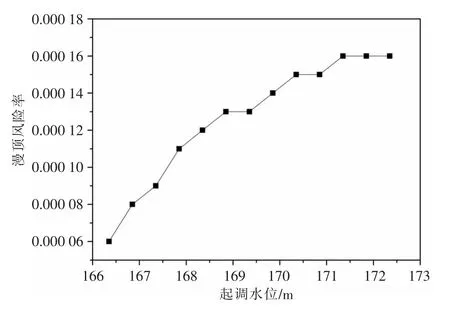
图4 不同运行方式的漫顶风险

3.3 调度运行方式选取

分析双牌水库在不同运行方式的漫顶风险率（图4），对比大坝社会可接受风险10-5和可容忍风险10-4的量级[11～12]，按保守取值，汛限水位确定为167.351 m，比现行设计汛限水位高出1.0 m，发生漫顶风险的概率在10-5量级，风险可以接受。另一方面，虽然起调水位较高时，漫顶风险在10-4量级，但是水库在水位高时，下泄流量大，增加了下游的防洪负担，防洪作用发挥得小，所以汛限水位可确定为167.351 m，可以保证漫顶风险小相对下泄流量也较小；随着洪水预报精准度的提高，可以加强水库上下游的洪水预报，汛限水位可以动态控制在167.351～168.351 m之间，随着起调水位的变化，漫顶风险率变化相对较小，大坝安全状态较平稳。

若汛限水位确定为167.351 m，比现行设计汛限水位高出1.0 m，经测算主汛期期间可多蓄水2 700万m3，可多发电1 490万kW·h。