采动下沉盆地压缩区斜交框架桥受力性能

窦国涛， 夏军武， 于文杰

(1.郑州航空工业管理学院土木建筑学院， 郑州 450046； 2.中国矿业大学，江苏省土木工程环境灾变与结构可靠性重点实验室， 徐州 221008； 3.中国矿业大学力学与土木工程学院， 徐州 221116)

针对采动区框架桥与土体方面，夏军武等[1]、于广云[2-4]、温庆杰等[5]、罗杰等[6]和Sheng等[7]根据煤矿采动区地表沉陷变形规律和铁路桥结构特征，建立了合理的数值计算模型，研究了地下开采引起的地表移动变形对原桥体结构和地基产生的附加内力和附加变形的规律，提出了在原箱形跨中加设钢筋混凝土支撑墙，提高箱体的承载能力，确保在采动引起的地表不均匀、大幅度沉陷过程中桥体的安全可靠和正常使用，为采动区的桥梁保护提供了科学依据。陈倩倩等[8]根据采动区地表沉陷变形规律和框架桥结构特征，建立了合理的数值计算模型，研究了地下开采引起的地表移动变形对原桥体结构和优化结构产生的附加内力的变化规律，以及基底附加应力变化和位移变化规律。苑国强[9]以矿区桥涵工程受开采沉陷影响的安全监测与评估为背景，通过数值模拟、理论分析对组合框架桥在开采沉陷影响下的内力演化规律进行分析研究。沈英男[10]以处于采煤沉陷区的某矿区组合框架桥为原型，建立了组合框架桥力学模型，研究不同地基倾斜下沉和竖向荷载情况下组合框架桥的承载特性，组合框架桥结构变形与地表倾斜变形的关系。 徐德志[11]以采煤沉陷区既有框架桥加高工程为研究背景，设计一种可升式钢结构作为既有框架桥的加层结构，并分析了所设计结构受开采沉陷影响的静力响应、动力特性和稳定性，同时针对钢结构稳定性提出优化方案。文献[12-14]也针对采动区框架桥与土体相互作用进行了一定的研究。徐博等[13]结合煤矿区公铁立交桥实际受采动影响情况，通过有限元建模对原桥在地表变形作用下的应力水平、应力分布和危险域进行分析，提出了桥体抗变形加固方案，并对加固后桥体进行建模分析。于文杰等[14]研究了采空区框架桥侧墙所承受的侧向土压力随墙体高度及外摩擦角的变化规律，采用库伦土压力理论进行了理论分析，结果表明当框架桥位于压缩区时，侧墙土压力值在被动土压力和静止土压力间的某一值；当框架桥位于拉伸区时，其土压力值位于静止土压力和主动土压力之间。

针对斜交框架桥方面，赵海涛等[15]以宁波市环城南路下穿铁路斜交框架桥项目为依托，利用 ANSYS 有限元软件建模，分析了斜交框架桥在养护期的应力场分布特点与规律，并得出了斜交角度对其应力场分布的影响。李森等[16]研究了设计参数对铁路斜交框架地道桥受力特性的影响，依托某实际工程，建立数值模型进行分析。以原结构为基础，分别改变框架地道桥的宽跨比、斜交角、高跨比、腋角尺寸并分别建立有限元模型计算分析，研究设计参数增长15% 时受力特性的变化规律。

还有学者针对温度对框架桥的影响进行了研究。杨青山等[17]针对混凝土浇筑初期框架桥温度裂缝产生的问题，结合现场试验及有限元模拟，探究了框架桥混凝土升温初期，腹板外、中、内侧温度变化；同时分析了应力状态条件下混凝土层面可能出现的开裂隐患。

目前，关于矿区斜交框架桥的研究较少，但实际工程中，由于路线原因，矿区框架桥通常既有正交框架桥，又有斜交框架桥，当煤层开采时，地表将形成下沉盆地，进一步通过土压力的传递会影响到框架桥的力学性能。为此，将进行研究采动区下沉盆地压缩区土压力对正交框架桥和斜交框架桥的受力性能的影响，并进行对比分析。

1 工程背景

由于采动工况众多，主要针对地下煤层水平，倾向充分采动，走向为充分采动这一特定工况进行研究，当地下煤层开采进行到采深(H0)的1/4～1/2时，采动将会扰动到地表土体，在采动区的上方形成下沉盆地[18]。下沉盆地通常分为压缩区和拉伸区。

针对矿山开采沉陷预计，中国最广泛采用的是概率积分法[18]。为研究沿地表移动盆地走向主断面的移动与变形情况，假定此时煤层倾向充分采动，煤层的开采厚度为m0, 开采深度为H0，开采长度为l，则依据概率积分法可知走向主断面的地表移动的预计公式为

(1)

式(1)中：U(x)为单元水平移动；x为计算点的走向坐标值；b为水平移动系数；W0为地表最大下沉值；r为主要影响半径。

图1为采空区下沉盆地地表位移曲线，由图1分析可知，盆地中心O点处土体位移为0，O点左侧土体位移为正，表示土体向右移动；O点右侧土体位移为负，表示土体向左移动，则说明下沉盆地压缩区土体向盆地中心挤压。

如图2所示，当框架桥最终位于下沉盆地压缩区，框架桥中心和下沉盆地中心重合时，框架桥两侧土体将挤压框架桥，框架桥侧墙的侧土压力增大。侧土压力会在静止土压力和极限被动土压力之间变化，为非极限被动土压力(图3)，然而框架桥设计时的土压力通常采用主动土压力或静止土压力，并未考虑采动影响这一特殊工况，同时，实际工程中框架桥和路桥并非均是正交(图3)，其斜交角度的大小对其受力也会产生影响，将分析这两种因素下(侧土压力、斜交角度)框架桥的受力性能。

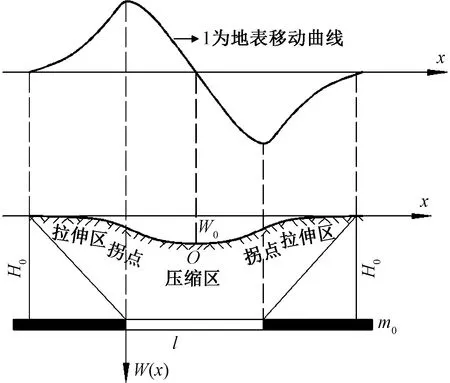
H0为埋深；m0为采厚；l为计算长度；W0为地表最大下沉值； W(x)为下沉值坐标图1 下沉盆地地表移动曲线Fig.1 Surface movement curve of subsidence basin

图2 下沉盆地压缩区框架桥Fig.2 Frame bridge in compression zone of subsidence basin

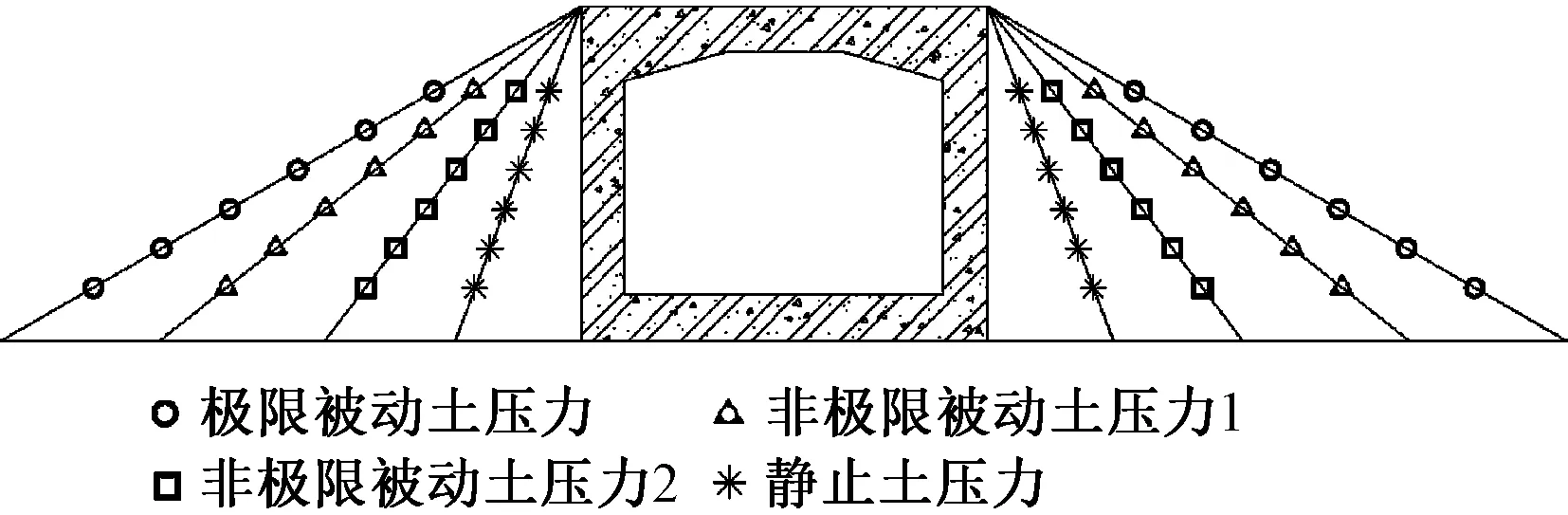
图3 压缩区框架桥侧土压力示意图Fig.3 Lateral earth pressure diagram of frame bridge in compression zone

2 有限元分析

2.1 工况设置

2.1.1 框架桥尺寸

采用正交框架桥和斜交框架桥分别进行分析，正交框架桥具体尺寸如图4所示，斜交框架桥具体尺寸如图5所示，斜交角度为15°。

2.1.2 框架桥侧土压力

框架桥周边土体参数如表1所示，通过静止土

图4 正交框架桥尺寸Fig.4 Dimensions of orthogonal frame bridge

图5 斜交框架桥尺寸Fig.5 Dimensions of skew frame bridge

压力公式可计算出其静止土压力分布，其计算公式为

p0=K0γz

(2)

式(2)中：p0为静止土压力；γ为土体重度，z为土体深度；K0为静止土压力系数，K0=1-sinφ，其中φ为土体内摩擦角。

通过库伦被动土压力公式，可计算出其被动土压力分布为

pp=Kpγz

(3)

式(3)中：pp为极限被动土压力；Kp为被动土压力系数。

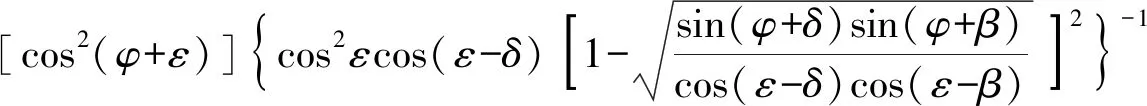
(4)

式(4)中：β为土体倾斜角；ε为墙体的倾斜角；δ为墙土之间的摩擦角，根据《公路桥涵设计通用规范》(JTG D60—2015)，通常取δ=φ/2。

通过式(2)～式(4)可计算出静止土压力系数(K0)、被动土压力系数(Kp)、非极限被动土压力系数(Kd)，取值如表1所示。

由于正交框架桥和斜交框架桥侧墙高度一致，周围土体参数取值一致，其土压力计算结果均一致(图6)。

表1 土体物理参数Table 1 Physical parameters of soil

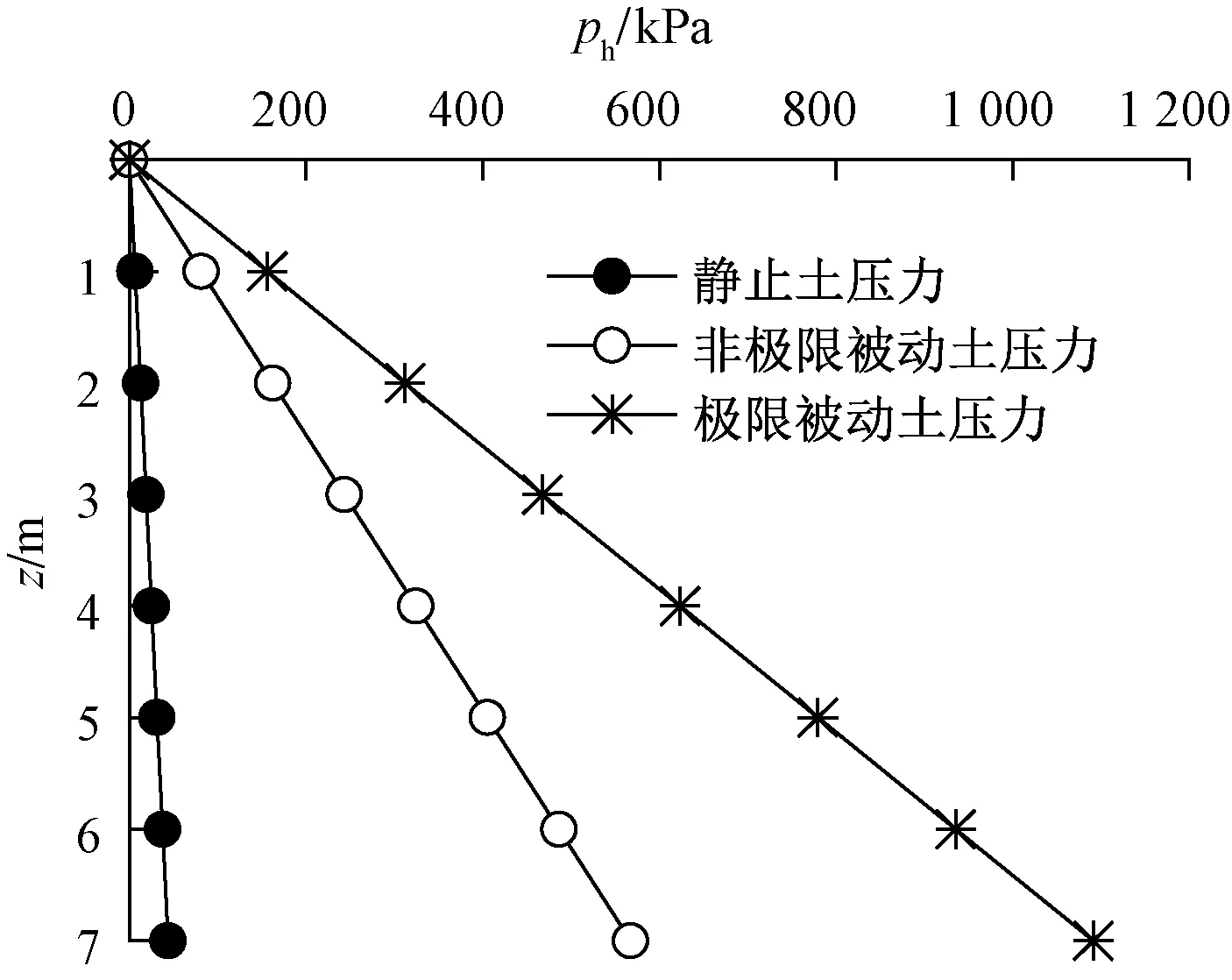
z为框架桥计算点地下深度；ph为水平向土压力图6 不同工况下框架桥侧土压力Fig.6 The horizontal earth pressure of frame bridgeunder different working conditions

2.1.3 工况汇总

共计6种工况，如表2所示。

表2 工况汇总Table 2 Summary of working condition

2.2 有限元模拟

采用ANSYS进行模拟计算，单元采用Solid65单元，钢筋混凝土采用整体式模型，底板约束住x、y、z方向的位移ux、uy、uz，材料参数如表3所示，只研究3种不同形式土压力作用下框架桥力学响应，未考虑其他作用，土压力以面荷载形式通过梯度荷载设置作用于框架桥侧墙上，框架桥有限元模型如图7所示。

图7 框架桥有限元模型Fig.7 Finite element model of frame bridge

表3 有限元模型材料参数Table 3 Material parameters of finite element model

3 结果

3.1 正交框架桥结果对比

图8为正交框架桥3种工况下x向位移云图对比。分析可知，在土压力作用下，框架桥侧墙中间区域产生位移最大，且随着土压力的增大而增大，提取其极值绝对值如图9所示，分析可知，在静止土压力作用下(工况1)，框架桥侧墙最大位移绝对值为0.234 mm；非极限被动土压力作用下(工况2)，框架桥侧墙最大位移绝对值为4.689 mm，为工况1的20.04倍；极限被动土压力作用下(工况3)，框架桥侧墙最大位移绝对值为7.117 mm，为工况1的30.41倍。

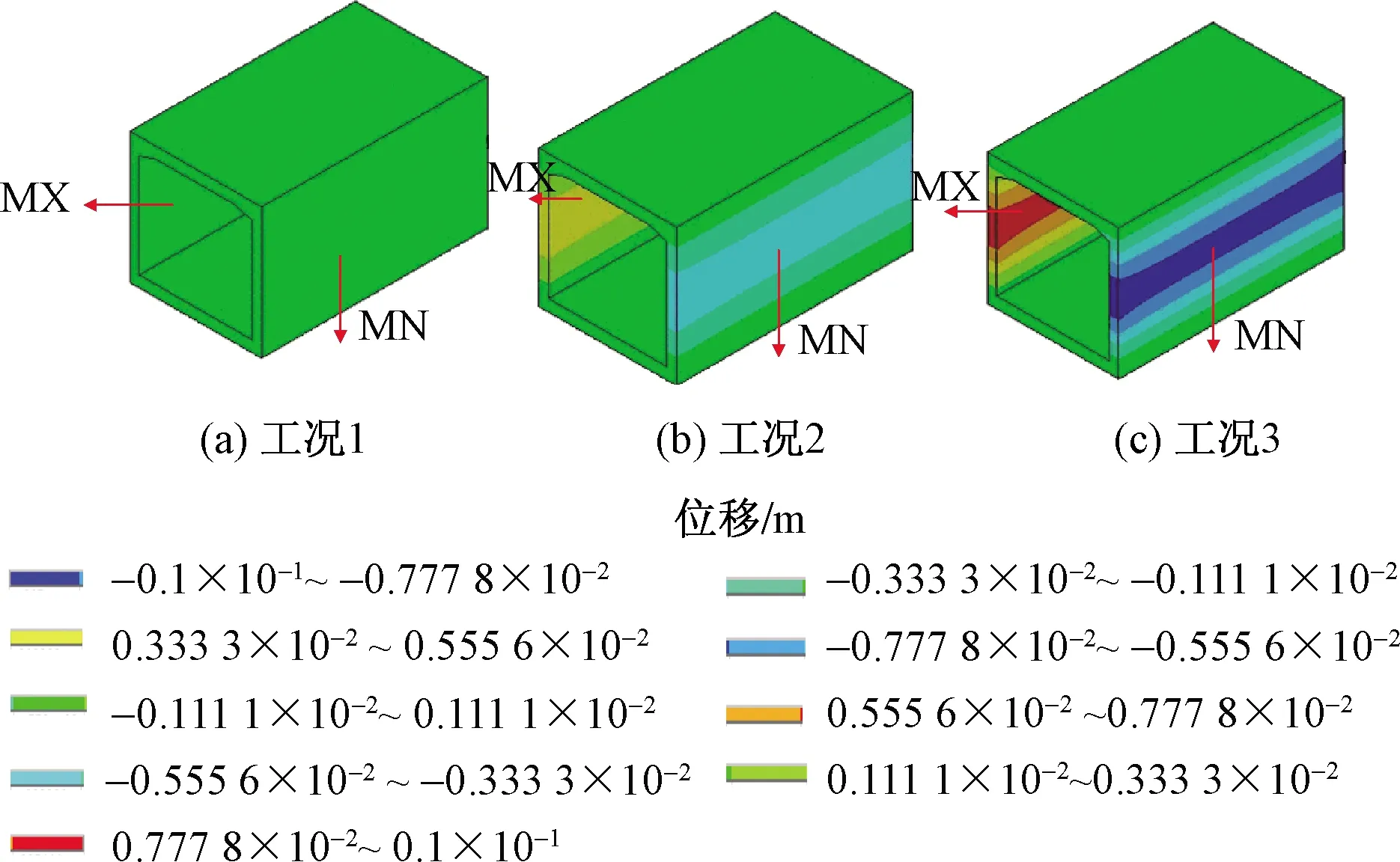
MN表示最小值；MX表示最大值图8 工况1～3的x向位移对比Fig.8 Comparison of x-direction displacement under condition 1～3

图9 工况1～3的x向位移极值绝对值对比Fig.9 Comparison of absolute value of x-direction displacement extremum under condition 1～3

图10为正交框架桥3种工况下y向位移云图对比，分析图中数据可知，工况1在侧墙下部区域产生位移最大，工况2和工况3框架桥顶板中间区域产生位移绝对值最大，且随着土压力的增大而增大，是由于静止土压力值较小，未完全抵消重力作用，顶板中间在重力作用下，尚未完全拱起，为统一对比，提取顶板位移极值绝对值如图11所示，分析可知，在静止土压力作用下(工况1)，框架桥顶板中间区域最大位移绝对值为0.061 6 mm；非极限被动土压力作用下(工况2)，框架桥顶板中间区域最大位移绝对值为3.398 mm，为工况一的55.16倍；极限被动土压力作用下(工况3)，框架桥顶板中间区域最大位移绝对值为6.852 mm，为工况1的111.23倍。

MN表示最小值；MX表示最大值图10 工况1～3的y向位移对比Fig.10 Comparison of y-direction displacement under condition 1～3

图11 工况1～3的y向位移极值绝对值对比Fig.11 Comparison of absolute value of y-direction displacement extremum under condition 1～3

图12为正交框架桥3种工况下米塞斯应力云图对比，框架桥侧墙和底板交界区域应力最大，且随着土压力增大而增大，将极值绝对值提出进行对比，如图13所示，分析可知，在静止土压力作用下(工况1)，框架桥最大米塞斯应力为1.14 MPa；非极限被动土压力作用下(工况2)，框架桥最大米塞斯应力为17.4 MPa，为工况1的15.26倍；极限被动土压力作用下(工况3)，框架桥最大米塞斯应力为34 MPa，为工况1的29.82倍。

因此，正交框架桥在土压力作用下，水平向位移最大值在框架桥侧墙中部区域；竖向位移最大值在框架桥顶板中间区域；最大米塞斯应力值在框架桥侧墙和底板交界处区域，当土压力从静止土压力增大到极限被动土压力过程中，以上参数极值绝对值出现的区域不变，但数值不断增大，此工况下框架桥进行加固设计时，土压力变化因素不可忽视。

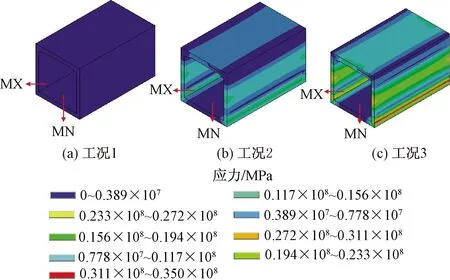
MN表示最小值；MX表示最大值图12 工况1～3的米塞斯应力对比Fig.12 Comparison of Mises stress under condition 1～3

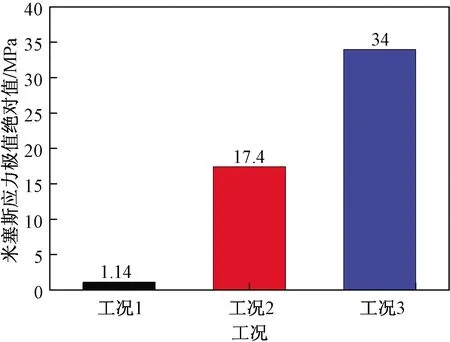
图13 工况1～3的米塞斯应力极值绝对值对比Fig.13 Comparison of absolute value of Mises stress extreme value under condition 1～3

MN表示最小值；MX表示最大值图14 工况4～6的x向位移对比图Fig.14 Comparison of x-direction displacement under condition 4～6

图15 工况4～6的x向位移极值绝对值对比Fig.15 Comparison of absolute value of x-direction displacement extremum under condition 4～6

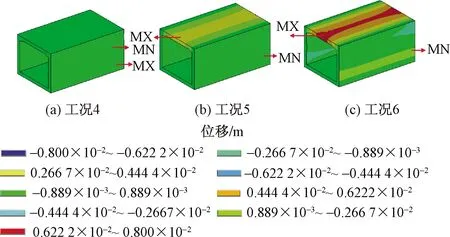
MN表示最小值；MX表示最大值图16 工况4～6的y向位移对比Fig.16 Comparison of y-direction displacement under condition 4～6

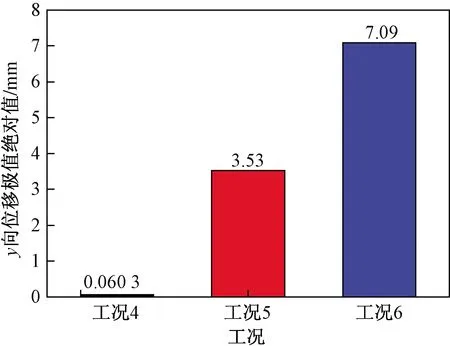
图17 工况4～6的y向位移极值绝对值对比Fig.17 Comparison of absolute value of y-direction displacement extremum under condition 4～6

3.2 斜交框架桥结果对比

图14为斜交框架桥3种工况下x向位移云图对比，分析可知，在土压力作用下，框架桥侧墙中间区域产生位移最大，且随着土压力的增大而增大，提取其极值绝对值如图15所示，分析可知，在静止土压力作用下(工况4)，框架桥侧墙最大位移绝对值为0.293 mm；非极限被动土压力作用下(工况5)，框架桥侧墙最大位移绝对值为5.373 mm，为工况4的18.34倍；极限被动土压力作用下(工况6)，框架桥侧墙最大位移绝对值为4.689 mm，为工况4的35.72倍。

图16为斜交框架桥3种工况下y向位移云图对比，分析可知，工况4在侧墙下部区域产生位移最大，工况5和工况6框架桥顶板中间区域产生位移最大，且随着土压力的增大而增大，是由于静止土压力值较小，未完全抵消重力作用，顶板中间在重力作用下，尚未完全拱起，为统一对比，提取顶板位移极值绝对值如图17所示，分析可知，在静止土压力作用下(工况4)，框架桥顶板中间区域最大位移绝对值为0.060 3 mm；非极限被动土压力作用下(工况5)，框架桥顶板中间区域最大位移绝对值为3.53 mm，为工况4的58.54倍；极限被动土压力作用下(工况6)，框架桥顶板中间区域最大位移绝对值为7.09 mm，为工况4的117.58倍。

图18为正交框架桥3种工况下米塞斯应力云图对比，框架桥侧墙和底板交界处区域应力最大，且随着土压力的增大而增大，将极值绝对值提出进行对比，如图19所示，分析可知，在静止土压力作用下(工况3)，框架桥最大米塞斯应力为1.14 MPa；非极限被动土压力作用下(工况4)，框架桥最大米塞斯应力为18.9 MPa，为工况1的16.58倍；极限被动土压力作用下(工况6)，框架桥最大米塞斯应力为36.8 MPa，为工况1的32.28倍。

MN表示最小值；MX表示最大值图18 工况4～6的米塞斯应力对比Fig.18 Comparison of Mises stress under condition 4～6

图19 工况4～6的米塞斯应力极值绝对值对比Fig.19 Comparison of absolute value of Mises stress extreme value under condition 4～6

由图14～图19可知，斜交框架桥在土压力作用下，水平向位移最大值在框架桥侧墙中部区域；竖向位移最大值在框架桥顶板中间区域(静止土压力工况在框架桥侧墙下部区域)；最大米塞斯应力值在框架桥侧墙和底板交界处区域，当土压力从静止土压力增大到极限被动土压力过程中，以上参数极值绝对值出现的区域不变，但数值不断增大，此工况下框架桥进行加固设计时，土压力变化因素也不可忽视。

3.3 正交框架桥与斜交框架桥结果对比

图20(a)为正交框架桥和斜交框架桥x向位移极值绝对值对比，斜交框架桥极值绝对值稍大于正交框架桥。静止土压力工况下，其比值为1.25；非极限被动土压力工况下，其比值为1.15；极限被动土压力工况下，其比值为1.47。

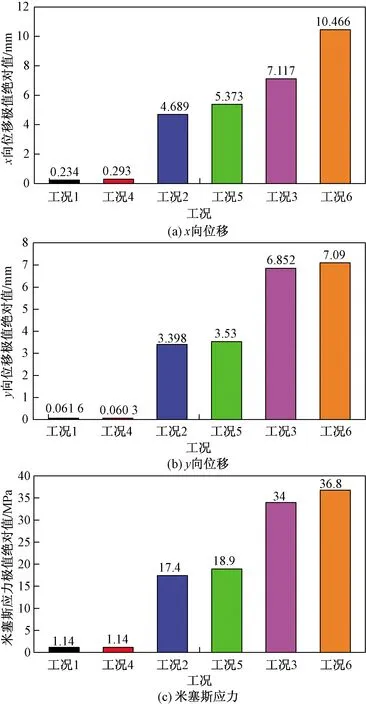
图20 正交框架桥和斜交框架桥x向位移、y向位移、 米塞斯应力极值绝对值对比Fig.20 Comparison of absolute value of x-direction displacement, y-direction displacement, Mises stress extreme value between orthogonal frame bridge and skew frame bridge

图20(b)为正交框架桥和斜交框架桥y向位移极值绝对值对比，除静止土压力工况外，斜交框架桥极值绝对值稍大于正交框架桥。静止土压力工况下，其比值为0.98；非极限被动土压力工况下，其比值为1.04；极限被动土压力工况下，其比值为1.03。

图20(c)为正交框架桥和斜交框架桥米塞斯应力极值绝对值对比，除静止土压力工况外，斜交框架桥极值绝对值稍大于正交框架桥。静止土压力工况下，其比值为1.00；非极限被动土压力工况下，其比值为1.09；极限被动土压力工况下，其比值为1.08。

4 结论

研究了采动区下沉盆地压缩区土压力对正交框架桥和斜交框架桥的受力性能的影响，得到如下结论。

(1)正交框架桥和斜交框架桥在土压力作用下，水平向位移最大值在框架桥侧墙中部区域；竖向位移最大值在框架桥顶板中间区域；最大米塞斯应力值在框架桥侧墙和底板交界处区域。

(2)正交框架桥当土压力从静止土压力增大到极限被动土压力过程中，以上参数极值绝对值出现的区域不变，数值不断增大，x向位移极值绝对值比值达到30.41；y向位移极值绝对值比值达到111.23；米塞斯应力极值绝对值比值达到29.82倍。

(3)斜交框架桥当土压力从静止土压力增大到极限被动土压力过程中，以上参数极值绝对值出现的区域不变，数值不断增大，x向位移极值绝对值比值达到35.72；y向位移极值绝对值比值达到117.58；米塞斯应力极值绝对值比值达到32.28倍。

(4)当土压力工况相同时，斜交框架桥位移和应力极值绝对值稍大于正交框架桥。

(5)采动区下沉盆地压缩区框架桥进行加固设计时，土压力变化因素不可忽视。