钢管混凝土柱-钢梁错层节点地震损伤评估
2021-05-31许成祥魏锦涛樊鸿博
许成祥, 魏锦涛, 樊鸿博, 郭 骁
(武汉科技大学城市建设学院, 武汉 430065)
随着现代建筑层数和跨度的不断增加,钢管混凝土结构越来越多地被应用到建筑结构当中,并取得了不少傲人的成就[1]。在工业建筑方面,由于建筑结构的功能需求,不可避免地产生了许多非规则的钢管混凝土框架节点,如变梁异型节点、变柱异型节点和错层节点[2]。近年来,许多学者开展了非常规钢管混凝土梁柱节点试验。许成祥等[3-4]进行钢管混凝土柱不等高梁节点试验,研究了该类节点的抗震性能。针对错层节点的研究,何微[5]、易丹[6]对钢筋混凝土错层梁柱节点进行了试验研究与分析。
目前,中外学者对钢管混凝土结构抗震性能的研究较多,但是对于其地震损伤的研究比较少。多数学者都是通过建立单参数和双参数损伤模型来表达构件的损伤,双参数地震损伤模型中应用较多的是Park-Ang模型[7-8]。中国研究者提出了一些适合钢筋混凝土构件或者型钢混凝土构件的双参数地震损伤模型[9-12],大多是基于Park-Ang模型修正或者改进而来的。但已经提出的双参数地震损伤模型适合钢管混凝土柱-钢梁错层节点的评价指标较少,有的损伤模型并未考虑加载路径对结构损伤的影响,并且部分损伤模型的物理概念不是很清楚。
结构在地震作用下损伤一般是由变形和累积耗能共同造成的,因此地震损伤模型都会采用变形项和能量项结合的表达式。基于钢管混凝土柱-钢梁错层节点抗震试验研究,考虑变形损伤和能量累积损伤在损伤演化过程中所占的权重不同,提出合适的双参数地震损伤模型。将试验所得的数据通过地震损伤模型计算其地震损伤指数。定量描述钢管混凝土柱-钢梁错层节点在地震作用下的损伤演化规律,从而对该节点进行损伤评估,为以后的钢管混凝土柱-钢梁错层节点的损伤研究提供依据。
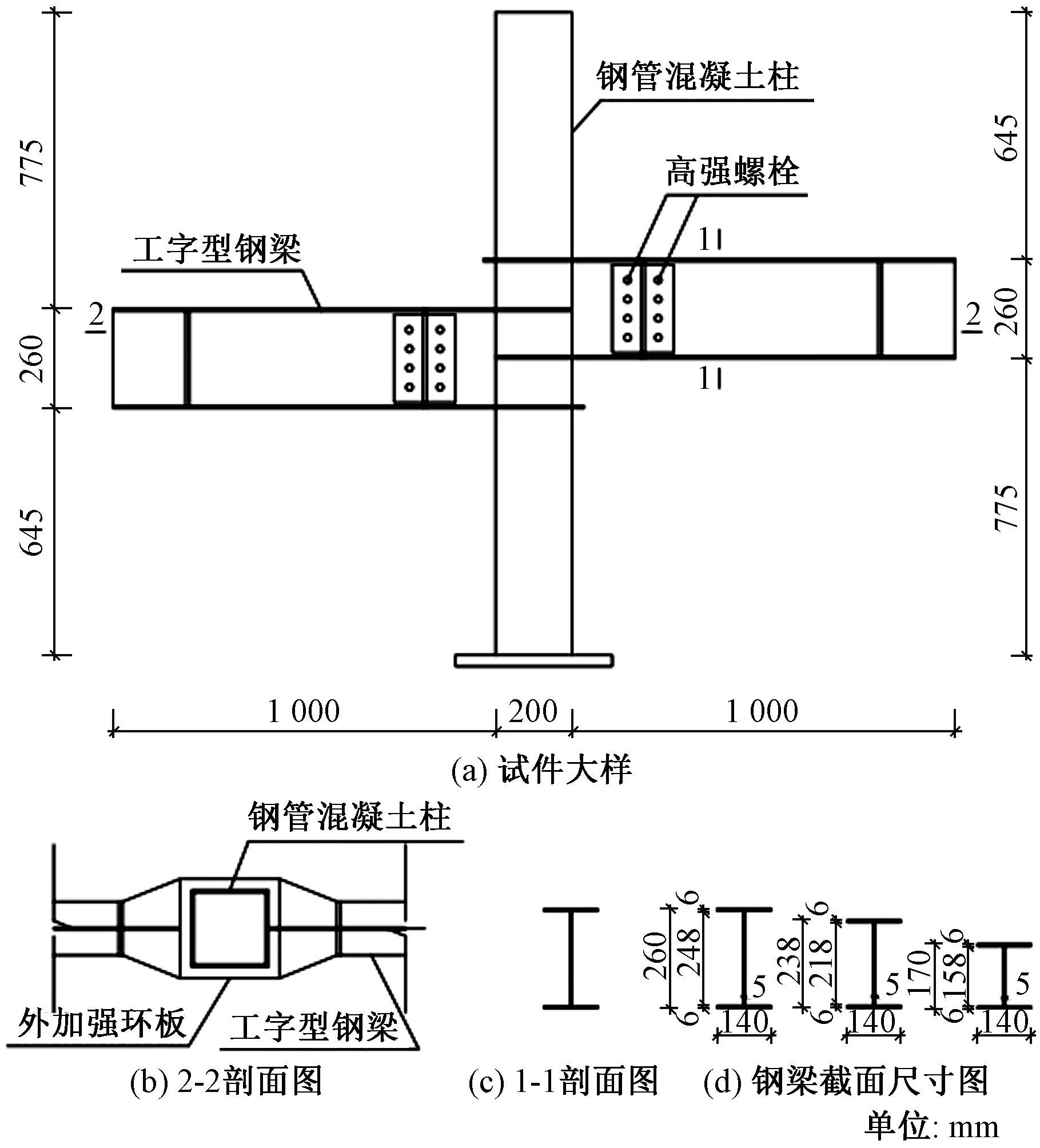
图1 试件几何尺寸及构造Fig.1 Dimension and details of specimen
1 试验概况
选取钢管混凝土柱-钢梁错层节点作为研究对象,设计了8个错层节点试件。试件的具体尺寸如图1所示。节点采用外加强环形式,按照“强剪弱弯、强节点弱构件”的原则设计。钢管柱和钢梁由Q235B级钢板焊接而成。钢管内的核心混凝土为C40商品混凝土。试件参数如表1所示,钢材力学性能实测值如表2所示。表2中,SJ-1、SJ-2、SJ-3、SJ-4、SJ-7、SJ-8为第一类错层节点,钢梁错开高度小于钢梁高度;SJ-5为第二类错层节点,钢梁错开高度等于钢梁高度;SJ-6为第三类错层节点,钢梁错开高度大于钢梁高度。加载装置及试验现场如图2所示。

表1 试件参数Table 1 Parameters of test specimens
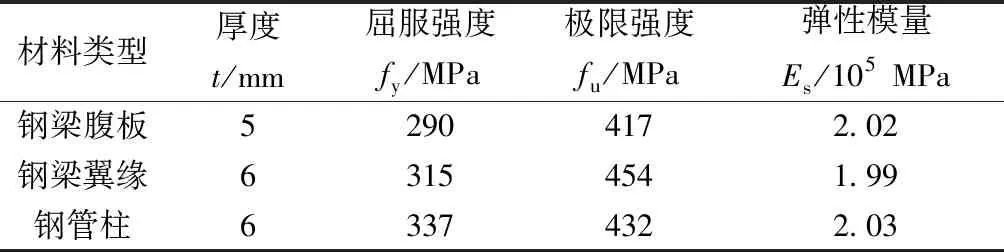
表2 钢材力学性能实测值Table 2 Material property of steel plates
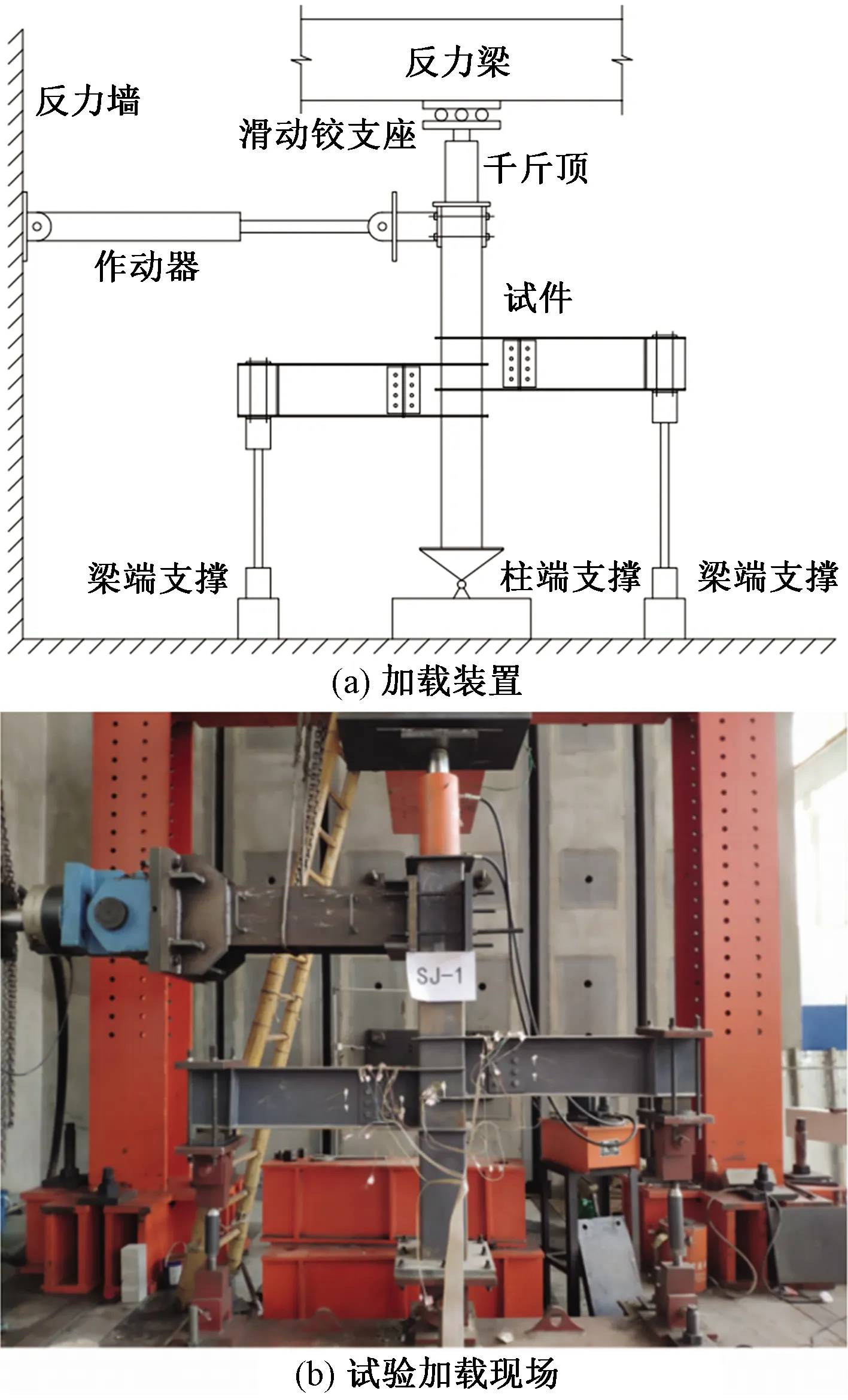
图2 加载装置及试验现场Fig.2 Loading device and test site
2 试件损伤过程
钢管混凝土柱-钢梁错层节点在低周往复荷载作用下的损伤是一个从无到有的逐渐演化的发展过程,可以分为三个阶段,试验现象如图3所示。以三类错层节点分别进行描述。

图3 各阶段试验现象Fig.3 Experimental phenomenon in each stage
2.1 第一类错层节点
2.1.1 无损伤阶段
无损伤阶段核心混凝土和钢管柱变形很小,外加强环和钢梁也未发生明显变形。试件此时还未屈服,错层节点骨架曲线的斜率没有变化,这一过程的损伤可以忽略不计,可以认为此过程没有损伤累积。
2.1.2 损伤稳定发展阶段
钢管柱屈服,核心混凝土和钢管柱变形逐步增大。伴随着咔嚓声,核心混凝土出现细微裂缝。随着荷载的增大,外加强环和钢梁的应变逐步增大,损伤也在逐步增大。右侧梁端上缘加强环板与翼缘连接处开始出现屈曲,从骨架曲线可以看出错层节点的刚度变化明显。此过程试件的地震损伤稳定积累。
2.1.3 损伤快速发展阶段
右侧梁端上缘加强环板与翼缘连接处出现倒“V”字形屈曲变形,屈曲破坏明显。右侧前方梁端下缘加强环板与柱端连接处应力集中,右侧外加强环板与钢梁翼缘连接处油漆出现脱落现象,左侧梁端后方下缘加强环板与柱端连接处出现焊缝断裂现象。水平施加荷载降至其峰值荷载85%以下,试件的刚度退化明显。可认为此阶段为损伤快速发展阶段。
2.2 第二类错层节点
2.2.1 无损伤阶段
无损伤阶段试件未发生明显变形,试件此时还未屈服,错层节点骨架曲线的斜率没有变化,这一过程的损伤可以忽略不计,可以认为此过程没有损伤累积。
2.2.2 损伤稳定发展阶段
右侧梁端上加强环板与翼缘连接处出现屈曲,损伤也在逐步增大。左侧梁端下加强环板与翼缘连接处出现屈曲变形。从骨架曲线可以看出错层节点的刚度变化明显。此阶段为损伤稳定发展阶段。
2.2.3 损伤快速发展阶段
上加强环板与翼缘连接处屈曲更加明显,呈倒“V”字形屈曲,加强环板与翼缘连接处出现焊缝断裂现象。水平施加荷载降至其峰值荷载85%以下,试件的刚度退化明显。此阶段为损伤快速发展阶段。
2.3 第三类错层节点
2.3.1 无损伤阶段
无损伤阶段梁柱变形很小,试件此时还未屈服,错层节点骨架曲线的斜率没有变化,这一过程的损伤可以忽略不计,可以认为此过程没有损伤累积。
2.3.2 损伤稳定发展阶段
反“Z”字形屈曲变形在右侧梁端上加强环板与翼缘连接处出现,右侧梁端上加强环板与翼缘连接处出现屈曲变形。试件处于弹塑性阶段,试件刚度退化明显。此阶段为损伤稳定发展阶段。
2.3.3 损伤快速发展阶段
右侧梁端上加强环板与翼缘连接处出现倒“V”字形屈曲变形,焊缝处油漆剥落焊缝断裂。水平施加荷载降至其峰值荷载85%以下,试件的刚度退化明显。此阶段为损伤快速发展阶段。
3 滞回曲线
通过低周往复试验测得柱子顶端位移和荷载的数据,分析整理得到钢管混凝土柱-钢梁错层节点的滞回曲线,如图4所示。错层节点的延性、承载能力、刚度与耗能等性能均可由滞回曲线来反映。
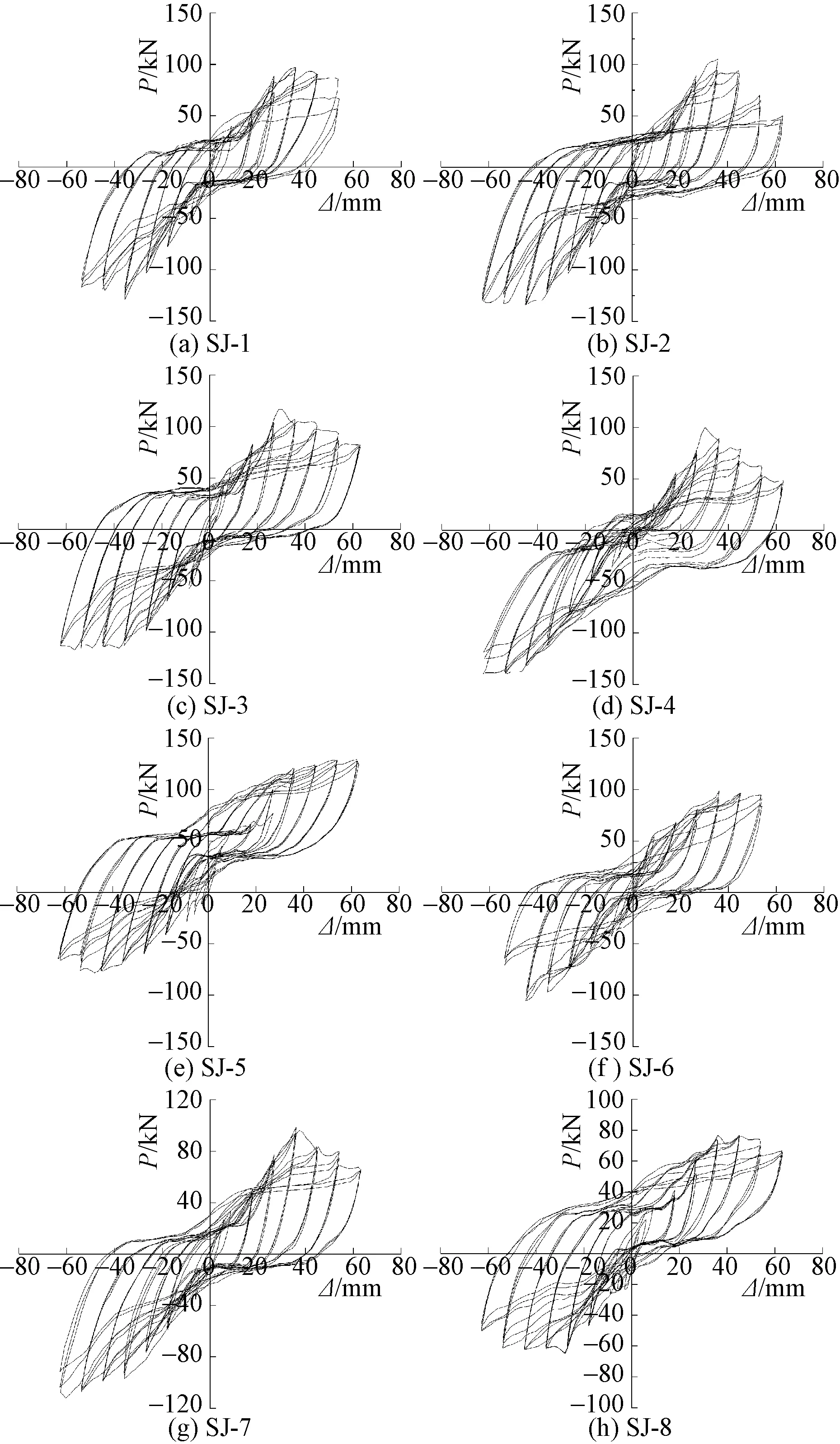
P为荷载;Δ为位移图4 荷载-位移滞回曲线Fig.4 Hysteretic loops of specimens
4 损伤模型的提出
损伤模型一般有3种类型:①通过变形来计算的位移型;②通过能量来控制的能量型;③结合位移和能量两个因素的位移能量型。 应用最多的地震损伤模型是Park-Ang损伤模型,该损伤模型的优势在于同时分析了位移和能量两个因素,属于第三种类型的损伤模型位移能量型。该损伤模型有大量的钢筋混凝土试验数据支持,其表达式为
(1)
式(1)中:δi为第i次荷载半循环间的最大变形;δu和Fy分别为单调荷载作用下极限变形和屈服强度;Ei为从初始时刻计的第i次荷载半循环的滞回耗能;N为加载半循环次数;D为构件的损伤指数;β为构件的耗能系数。
研究表明,随着损伤研究的深入,Park-Ang损伤模型有其局限性和不合理之处[13],主要是:①构件在加载初期未屈服时,还处于弹性受力阶段,此时构件的损伤指数为0,但是基于损伤模型计算的损伤指数不为0,当构件加载至破坏,基于模型计算的损伤值也不为1;②式(1)中β不太容易确定,Park等提出的关于β的表达式,目前只适用钢筋混凝土结构,对于型钢混凝土结构或者钢管混凝土结构,该模型并不适用;③该损伤模型同时研究了位移和能量两个参数,比单参数损伤模型合理一些,但是只是将位移项和能量项简单线性组合,对构件损伤的研究并不充分,将位移项和能量项进行非线性组合更合理一些。
因此,将文献[14]修正的Park-Ang 损伤模型,提出适合错层节点的地震损伤模型,基于变形和能量双重准则的地震损伤模型,其表达式为
(2)
式(2)中:η、λ为组合系数;δmax,j为第j次半循环所对应的最大非弹性变形;δy为构件的屈服变形。
5 模型参数
5.1 屈服点、极限点和破坏点
由于钢管混凝土结构的屈服点不容易确定,将采用几何作图法来确定屈服点,其确定方法如图5所示,OA与曲线相切于原点,Y点为屈服点,M点为极限荷载点,U点为破坏点。三点对应的横坐标是位移纵坐标为荷载。Δy、Δm和Δu分别为屈服位移、极限位移和破坏位移,Py、Pm和Pu分别为屈服荷载、极限荷载和破坏荷载。

图5 几何作图法Fig.5 Geometric drawing method
5.2 最大非弹性变形
非弹性变形一般指的是构件在弹塑性阶段或者塑性阶段的变形,构件从弹性阶段进入弹塑性阶段之后第一次出现的最大非弹性位移幅值被定义为最大非弹性变形。在低周往复荷载作用下,当构件正负向位移小于之前达到过的最大位移,可认为该位移幅值对构件的损伤影响不大;反之,该循环的损伤值等于之前的损伤值加上本次变形损伤项和能量损伤项一起相互影响导致的损伤值。对于损伤研究来说,加载路径的不同也是造成构件损伤的因素之一,最大非弹性变形的定义恰好能解决加载路径对构件的影响。
5.3 累积耗能能力
在研究结构在地震作用下的耗能能力时,一般定义某一次位移循环的滞回曲线包围的面积为该循环所耗散的能量。如图6所示,选取某一循环下的滞回环,横坐标以上的阴影区域面积等于第i次半循环的耗能能力Ei,此时第i次半循环的累积耗能能力等于之前能量耗散的总和加上Ei。横坐标以下的阴影区域的面积等于第i+1次半循环的耗能能力Ei+1,第i+1次半循环的累积耗能等于构件之前的能量耗散加上整个滞回环的面积。Fi、δi分别为第i次半循环的荷载和位移,Fi+1、δi+1分别为第i+1次半循环的荷载和位移。在弹塑性阶段或者塑性阶段,如果构件的变形并没有超过之前某一循环的变形,可以不考虑变形项的损伤,但是这一循环的滞回耗能对能量项的贡献不能被忽略。

图6 某一滞回环的特征参数Fig.6 Characteristic parameters of a hysteresis loop
5.4 参数回归
从理论上来讲,当构件没有损伤时,损伤值D=0,构件处于弹性阶段;当构件完全破坏时,损伤值D=1;当0 通过计算可以得到η的平均值为0.15,并且当η=0.15时,组合系数λ的离散性较小,因此,取组合系数η=0.15。对组合系数λ考虑了轴压比n,错开高度h,剪压比βV,其表达式为 λ=0.184-0.052 8n+0.000 2h+0.165 2βV (3) 基于上述所建立的损伤模型,结合钢管混凝土柱-钢梁错层节点地震损伤试验的数据,计算各个构件在特征点的损伤指数,并和试验结果进行了比较,如表3所示。可以发现基于所提出的地震损伤模型计算的结果和试验结果比较吻合,表明所提出的双参数损伤模型能够较好地反映低周往复作用下钢管混凝土柱-钢梁错层节点的损伤从无到有的全过程。 表3 计算值与试验值的对比 图7为不同轴压比下钢管混凝土柱-钢梁错层节点的地震损伤随着循环数的增加而增大,如图7所示,对比试件SJ-1、SJ-3,可以发现轴压比小的试件的损伤发展与累积大于轴压比大的试件,轴压比对抑制试件的损伤发展起到一定的作用,能够有效阻止错层节点核心混凝土裂缝的产生。 图7 轴压比对试件损伤的影响Fig.7 Influence of axial compression ratio on damage of specimens 图8为不同错开高度下钢管混凝土柱-钢梁错层节点的地震损伤随着循环数的增加而增大,试件SJ-5和SJ-6的轴压比和剪压比一样。SJ-6的错开高度比SJ-5大,从图8可以看出,错开高度大的试件的损伤发展与累积大于错开高度小的试件。 图8 错开高度对试件损伤的影响Fig.8 Influence of staggered height on damage of specimens 图9为不同剪压比下钢管混凝土柱-钢梁错层节点的地震损伤随着循环数的增加而增大,SJ-1的剪压比大于SJ-7,从图9可以看出,剪压比大的试件的损伤发展与累积大于剪压比小的试件。 图9 剪压比对试件损伤的影响Fig.9 Influence of shear compression ratio on damage of specimens 通过对8个设计参数不同的钢管混凝土柱-钢梁错层节点进行地震损伤评估,得到以下结论。 (1)考虑到Park-Ang地震损伤模型并不能正确反映变形和能量对钢管混凝土柱-钢梁错层节点的损伤发展规律,通过加入组合系数,改进了Park-Ang地震损伤模型,得到了适用于钢管混凝土柱-钢梁错层节点的非线性双参数地震损伤模型。该双参数地震损伤模型能够较好地反映其在低周往复荷载作用下的损伤发展情况,对错层节点做出了比较客观的评估。 (2)影响钢管混凝土柱-钢梁错层节点损伤的因素有轴压比、错开高度、剪压比,本文模型考虑了这些参数对构件损伤过程的影响,并且考虑了加载路径对构件损伤的影响。给出了组合系数λ与构件设计参数的具体表达式,可用于指导该类节点的抗震设计。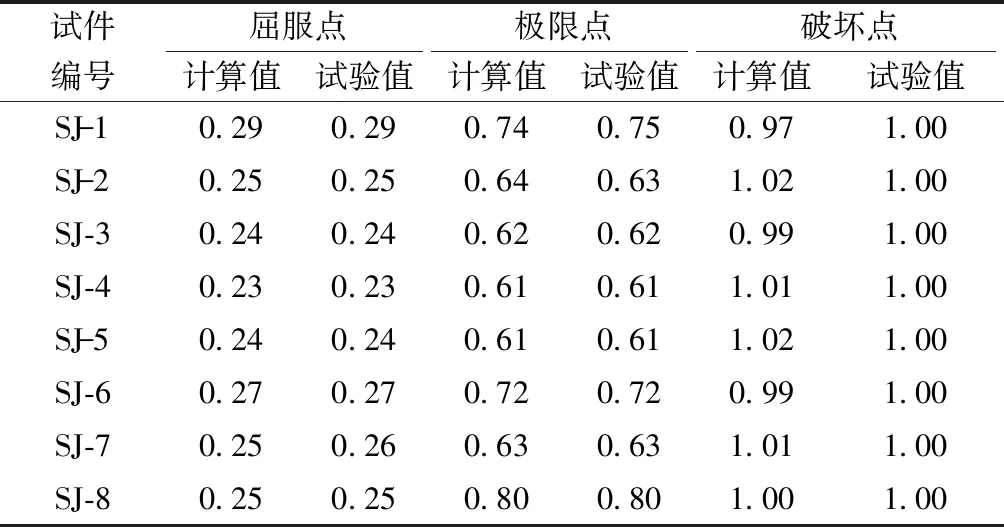
6 损伤影响因素分析
6.1 轴压比对地震损伤的影响

6.2 错开高度对地震损伤的影响

6.3 剪压比对地震损伤的影响

7 结论
