基于TGD/DCB改正的BDS多频单点定位精度分析
2021-05-31王潜心龚佑兴
李 坤,王潜心,龚佑兴,胡 超,苗 伟,程 彤
(1.中国矿业大学 环境与测绘学院,江苏 徐州 221116;2.国防科技大学 军事基础教育学院,湖南 长沙 410072)
北斗卫星导航系统(BeiDou Navigation Satellite System BDS)于2020年6月正式建设完成,目前第2代BDS卫星有3个信号频点,信号频率分别为1 561.098、1 207.140、1 268.520 MHz[1-2],第3代卫星增加了新信号b1c、b2a。卫星信号频点众多,对于多频组合定位,不同频点的硬件延迟偏差是对定位影响的重要因素。为了给BDS全球用户提供高精度的定位、导航及授时服务,需要解决码偏差对定位的影响。
目前,码偏差产品主要分为2类:① 广播星历播发的时间群延迟(time group delay,TGD)产品,② IGS分析中心提供的高精度后处理差分码偏差(differential code bias,DCB)产品[3-5],TGD产品相比于DCB产品,它的更新周期长,且精度低于DCB产品。国内的中国测绘科学研究院北斗分析中心也进行DCB产品的解算,其联合了MGEX测站和iGMAS测站的数据,采用和IGS分析中心相同的“零均值”基准约束,对观测数据进行后处理并向用户提供BDS的DCB产品[6]。文献[7]详细分析了TGD/DCB对标准单点定位(standard point positioning,SPP)和精密单点定位(precise point positioning,PPP)的影响,并推导出TGD/DCB的改正公式,给出TGD和DCB之间的关系;文献[8]对GPS/BDS/Galileo等卫星系统进行了多频伪距DCB改正的分析,并提出了三频伪距定位模型;文献[9]对BDS和GPS的单频和双频DCB改正进行了对比分析;文献[10]研究了DCB对单频PPP定位的收敛速度的影响,并对单频模型其余待估参数吸收DCB参数进行了分析。
目前,关于码偏差对定位精度的影响,针对单频和双频的分析成果较多,对于三频改正,已有对SPP定位精度的分析[8],而关于PPP的相关研究较少,但三频PPP定位模型充分利用了各频点的观测数据,具有很重要的研究价值。本文根据噪声放大最小原则推导出三频PPP码偏差改正模型,详细分析了多频SPP、PPP的 TGD/DCB改正模型对定位精度的影响,针对三频PPP,分析了其待估参数对码偏差的吸收情况。
1 单点定位TGD/DCB改正模型
1.1 SPP双频TGD/DCB改正模型
对于SPP,不考虑多路径误差和观测噪声误差,BDS 3个频点的伪距方程可简化为:
(1)
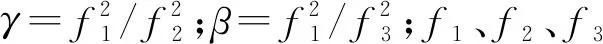
BDS的广播星历钟差和精密星历钟差基准解算不一致,广播星历是以B3频点为基准,而精密星历则是以B1B2无电离层解算作为时间基准[8]。广播星历中含有B3频点的硬件延迟钟差参数,其可以表示为:
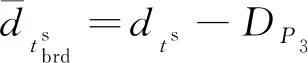
(2)
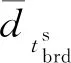
(3)
根据(1)~(3)式,可得BDS单频伪距的DCB改正公式如下:
(4)
根据BDS发布的最新版空间信号接口控制文件(interface control document,ICD),可得B1、B2波段含TGD参数TGD的伪距改正公式[12]为:
(5)
根据(4)式、(5)式可以得出:
(6)
根据(4)式,对(5)式进行组合消去电离层误差,并由(6)式TGD和DCB的关系,可得各频点的双频无电离层组合。因为B2、B3波段的频率相近,在进行无电离层组合改正时,组合系数高达14.29,导致组合后的噪声过于放大,无法定位[13],所以本文不再考虑B2、B3频点的无电离层改正公式。其余频点无电离层组合TGD/DCB改正公式[14]为:
(7)
1.2 PPP双频TGD/DCB改正模型
PPP使用的钟差产品是以B1B2无电离层组合作为时间基准,在解算过程中并未考虑硬件延迟偏差的影响。卫星精密钟差产品与硬件延迟偏差的关系[14]为:
(8)
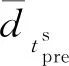
(9)
根据(9)式和(6)式,可得PPP各频点双频无电离层组合的TGD/DCB改正公式[7]为:
(10)
1.3 三频TGD/DCB改正模型
对三频无电离层组合观测模型,根据三频无电离层组合观测理论[8]可得其模型如下:
PC123=(a+b+c)(ρ+dtro+dtr-dts)+
μC123dion+DP1P2P3
(11)
其中:PC123为组合观测值;a+b+c为组合系数;μC123为电离层延迟放大因子;DP1P2P3为组合硬件延迟。
对于无电离层组合,为了能唯一确定组合系数解,三频无电离层组合观测方程要满足以下要求:① 方程的距离几何系数应恒为1;② 能够消除一阶电离层误差;③ 对于噪声系数,考虑到对定位效果的影响,应该越小越好[15]。上述要求可以简化为如下约束方程[8]:
(12)
根据上述约束方程,可求得组合系数为:a=2.566,b=-1.229,c=-0.337。
根据组合系数和(4)式可得SPP三频组合的TGD/DCB改正公式[8]为:
(13)
根据组合系数和(9)式可得PPP三频组合的TGD/DCB改正公式为:
(14)
2 数据处理与实验分析
为具体分析对于SPP定位模式和PPP定位模式TGD/DCB改正的影响差异,选用2019年4月1日3个IGS测站(cusv、dgar、jfng)的数据,分别使用广播星历播发的TGD产品和中国测绘科学研究院解算的DCB产品对BDS卫星端的码偏差进行多频SPP和PPP定位实验。3个IGS测站均可接收B1/B2/B3频点信号,其基本信息见表1所列。

表1 测站基本信息
下文中:“corr-no”表示未进行DCB或TGD改正;“corr-tgd”表示码偏差改正参数使用的是TGD;“corr-dcb”表示改正参数使用的是DCB。
2.1 SPP
对于SPP定位模式,采用上述3个IGS测站数据分别进行双频和三频定位实验,利用(7)式和(13)式进行TGD和DCB的改正。所用的精密钟差和轨道文件是德国地球科学研究所(GeoForschungsZentrum,GFZ)解算的30 s和5 min采样间隔的最终产品,ERP和SNX文件为IGS解算的最终产品。DCB产品文件名格式为CAS0MGXRPA-yyyydoyxxxx-DCB.BSX。
B1B2B3组合平面残差结果和U方向残差结果,分别如图1、图2所示。
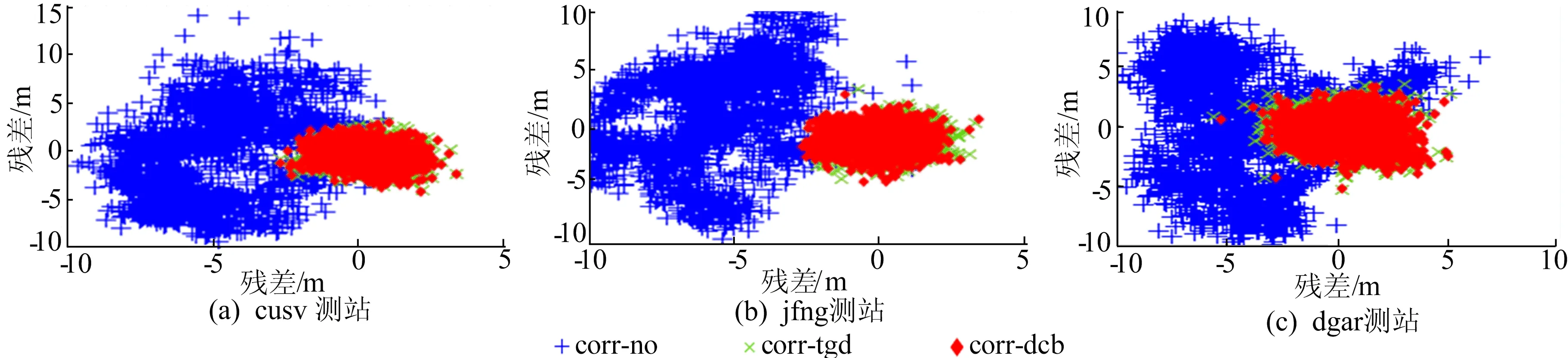
图1 B1B2B3组合观测值平面位置残差
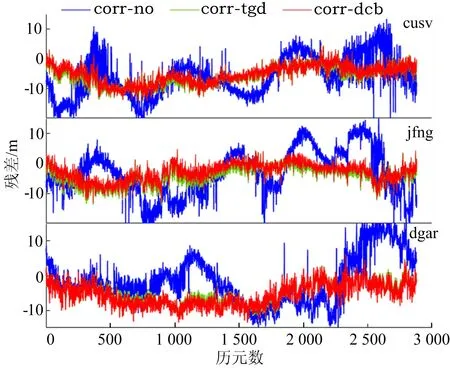
图2 B1B2B3组合观测值U方向残差
从图1、图2可以看出:① TGD/DCB对SPP定位精度影响比较显著,经TGD和DCB改正后的SPP定位精度,平面精度优于5 m,U方向精度优于10 m;② DCB改正略优于TGD改正,其原因可能是TGD的精度低于DCB,且TGD参数的更新周期长。
3个测站多种频点组合E、N、U3个方向的均方根误差(root mean square,RMS)见表2所列。
由表2可知:① TGD/DCB对SPP的影响为m级,B1B2组合由TGD改正的平面方向和U方向平均RMS分别为1.539、5.923 m,DCB改正平面方向和U方向平均RMS分别为1.528、5.644 m;② B1B3组合由TGD改正的平面方向和U方向平均RMS分别为1.906、6.020 m,DCB改正平面方向和U方向平均RMS分别为1.831、5.797 m;③ B1B2B3组合由TGD改正的平面方向和U方向平均RMS分别为1.559、5.846 m,DCB改正平面方向和U方向平均RMS分别为1.546、5.609 m。
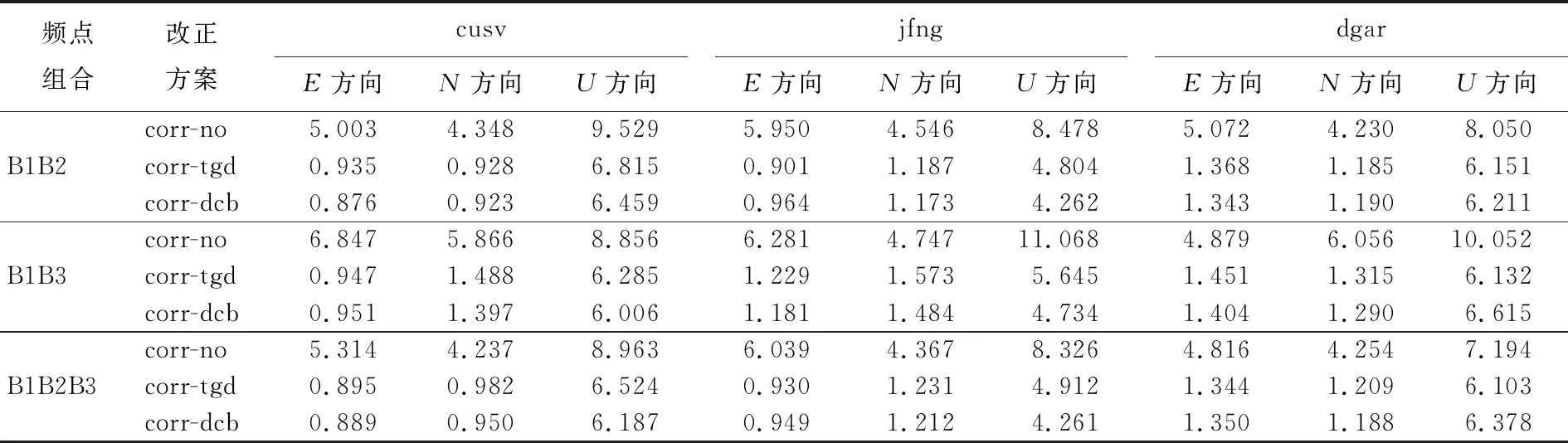
表2 3个测站多频SPP的RMS m
各频点组合定位精度提升率见表3所列。从表3可以看出,SPP的E、N方向定位精度提升大于70%,U方向定位精度提升大于28%。
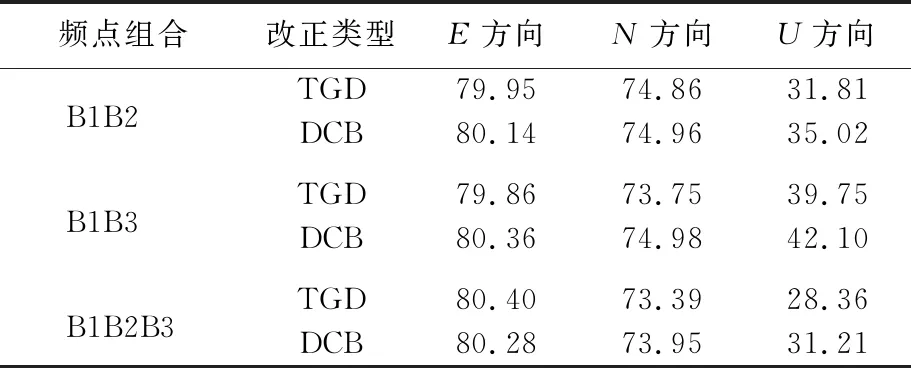
表3 多频SPP定位精度提升率 %
从SPP定位实验结果可以看出,B1B2组合的精度要优于B1B3组合,B1B2组合的精度和B1B2B3组合大体相当,这是因为本文涉及B1B2、B1B3、B1B2B3组合的噪声放大系数分别为2.897、3.527、2.865,B1B3组合的噪声放大系数大于另外2种组合的相应值,导致B1B3组合的精度低于另外2种组合。
2.2 PPP
对于PPP定位模式,采用3个IGS测站进行PPP实验,TGD/DCB所用的产品和SPP相同,TGD/DCB分别由(10)式、(14)式进行改正。
3个IGS测站各频点组合改正PPP定位实验RMS结果见表4所列。
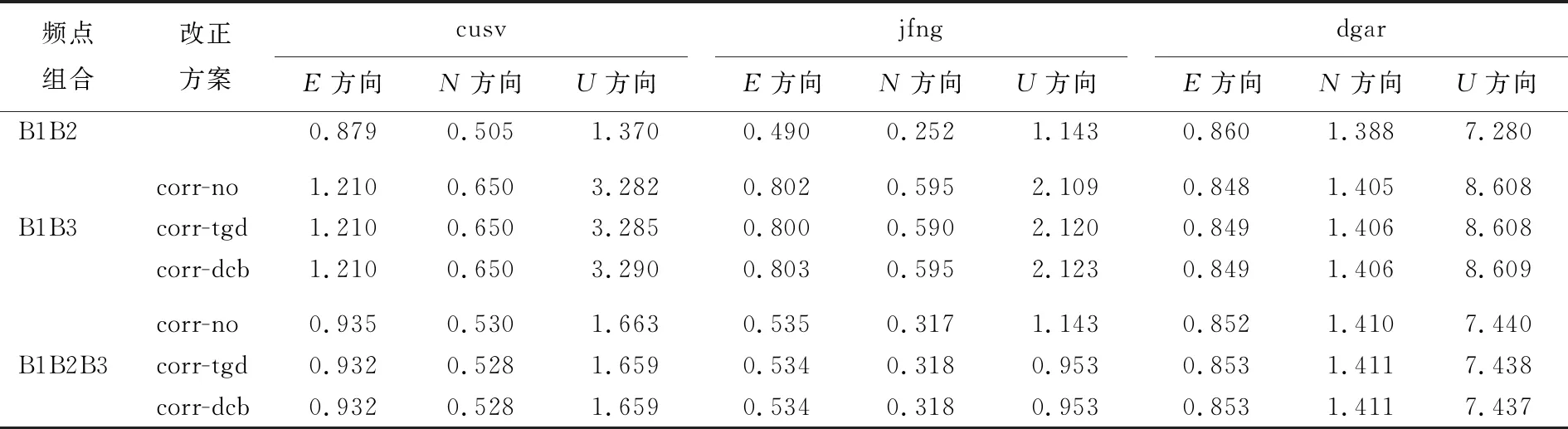
表4 3个测站多频PPP的RMS cm
由表4可知:① 多频PPP定位精度为cm级,TGD/DCB改正对定位精度提升不明显;对于B1B2组合,E、N、U方向平均RMS为0.743、0.715、3.264 cm;② B1B3组合,E、N、U方向平均RMS为0.953、0.883、4.671 cm;③ B1B2B3组合,E、N、U方向平均RMS值为0.774、0.752、3.415 cm。
dgar测站B1B2B3无电离层组合前100历元的结果如图3所示。
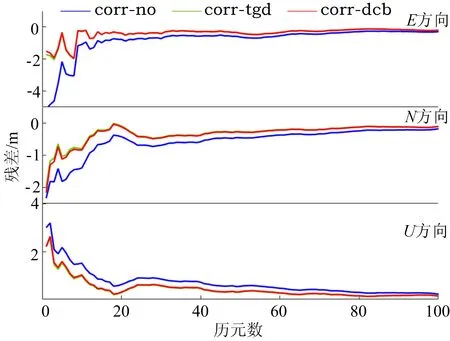
图3 dgar测站前100历元结果
从图3可以看出,未进行TGD/DCB改正的PPP定位组合,初始历元残差要大于组合残差,可见TGD/DCB改正后,提高了滤波的收敛速度。
对于未进行TGD/DCB改正的PPP定位模型,其误差在定位时会被其他待估计参数吸收。针对本文提出的B1B2B3无电离层组合模型,为探究模型中的待估参数对码偏差的吸收效果,下面分别分析接收机钟差、天顶对流层延迟及模糊度受到TGD/DCB改正的影响情况。
dgar测站B1B2B3组合接收机钟钟差经TGD或DCB改正前、后的差值如图4所示,dgar测站天顶对流层延迟经TGD或DCB改正前、后的差值如图5所示,各卫星模糊度差值的RMS统计如图6所示。
由图4可知,在进行B1B2B3组合定位时,接收机钟差差值最高达到1.5 m左右,滤波趋于收敛后的接收机钟差差值在0.5 m左右。由图5可知,天顶对流层延迟差值最高超过0.15 m,滤波趋于稳定后,改正前、后的对流层延迟大致相等。从图6可以看出,各颗卫星模糊度差值的RMS均小于1.0 m,最大超过0.9 m,除C08卫星外,其余均超过0.3 m。
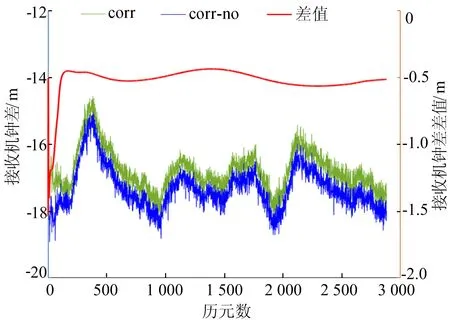
图4 dgar测站接收机钟差差值
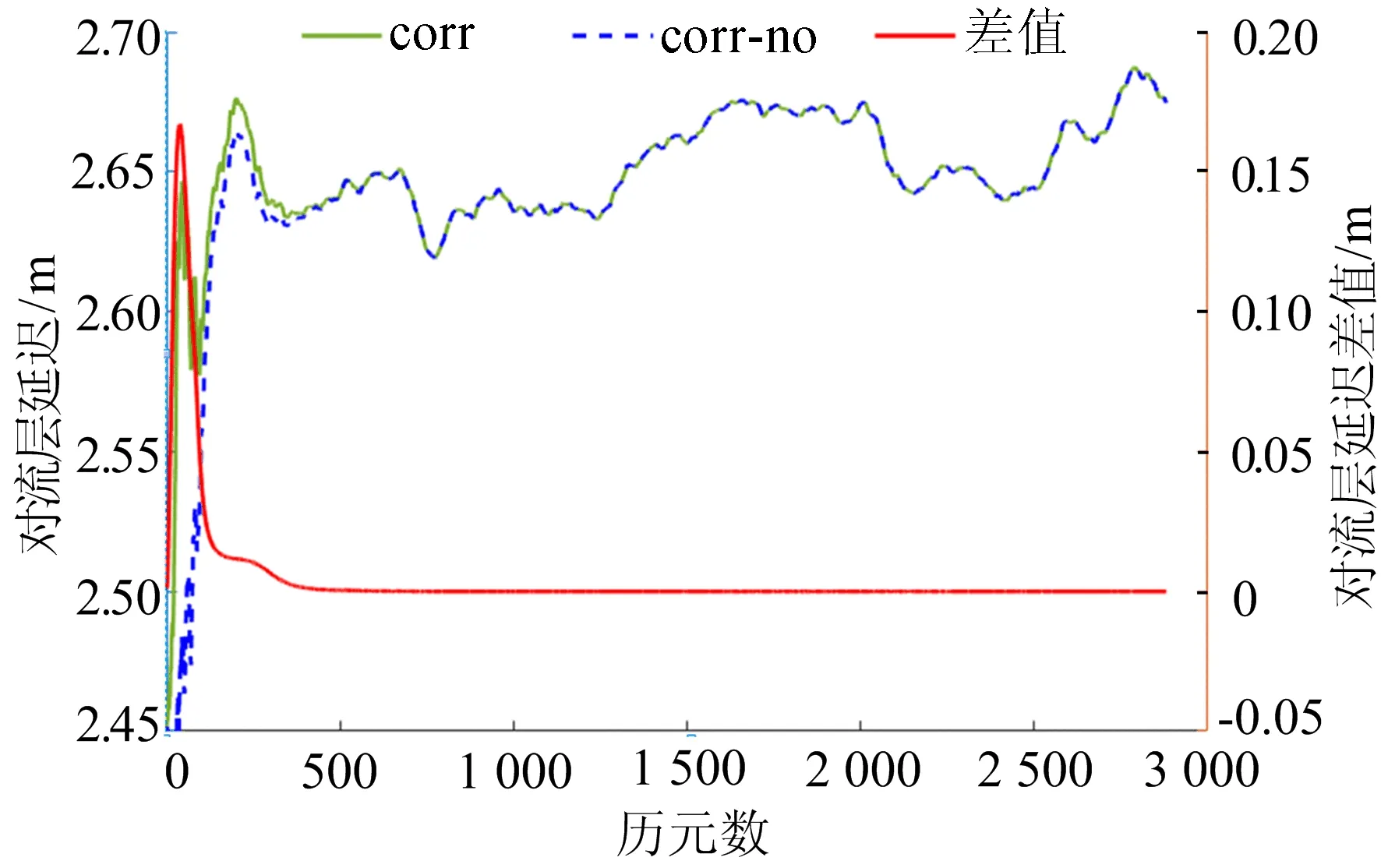
图5 dgar测站天顶对流层延迟差值
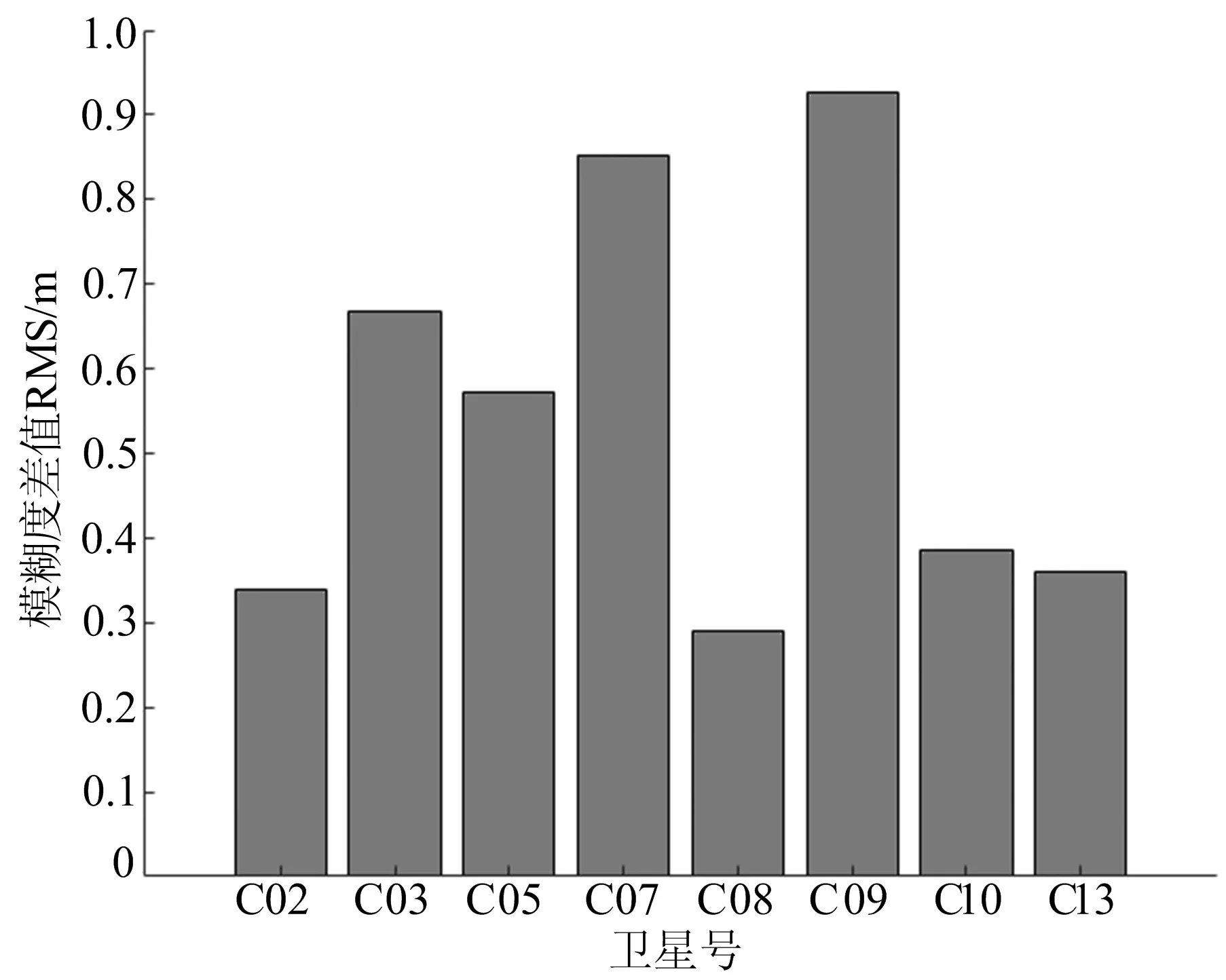
图6 dgar测站模糊度差值RMS统计
由上述结果可以得出,对于B1B2B3无电离层组合而言,接收机钟差和模糊度参数对TGD/DCB参数的吸收较为明显,天顶对流层延迟受TGD/DCB改正影响不大。
3 结 论
(1) TGD/DCB改正对SPP定位精度提升显著,改正精度量级达到m级,经改正的SPP定位精度平面方向小于5 m,U方向小于10 m;对于B1B2B3组合,经DCB改正的定位精度优于TGD改正,可能是由于TGD的更新周期长且精度低于DCB。
(2) TGD/DCB改正对PPP定位精度的提升效果不明显,但可以加快滤波的收敛速度;对于三频PPP,接收机钟差和模糊度吸收了绝大部分TGD/DCB误差。
(3) 由于B1B2、B1B3、B1B2B3组合的噪声放大系数分别为2.897、3.527、2.865,对定位精度的影响较大,因此,对于SPP,不同频点组合TGD/DCB改正模型的定位精度存在一定的差异。
