管线渗漏对地铁盾构影响的模型试验研究

2021-05-31汪维东黄晓康朱大勇

合肥工业大学学报（自然科学版） 2021年5期

汪维东,黄晓康,,朱大勇,周刚

(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.芜湖市轨道(隧道)交通工程质量安全监督站,安徽芜湖 241060)

0 引言

在城市地下空间开发与利用的过程中,地铁作为轨道交通系统,是其中的重要组成部分,并且是现代城市轨道交通发展的主流和方向。因管线渗漏诱发的工程事故占有较大比重,且其发生突然、危害性大,直接影响地铁建设的正常进行,严重威胁着城市的生产和生活,这已引起社会各界的广泛关注。

目前,对于隧道盾构施工引起的管线渗漏,相关研究较多。文献[1-3]利用平面应变模型试验,研究了因隧道施工扰动地下管线渗漏对地面坍塌造成的影响,发现管线渗漏水范围是直接影响地面坍塌与地层破坏剧烈程度的主要因素,渗漏范围越大,隧道开挖后造成的地面坍塌程度就越大;文献[4]基于复变函数的共形变换方法,综合解析法与数值法,求解稳定渗流时饱和土体二维渗流的基本微分方程,得出当盾构隧道发生侧向渗漏水时,周围土壤孔隙水压力在1倍隧道中心水平向埋深的范围内发生较大变化,且渗漏水范围越大,其衰减速度越显著;文献[5-6]采用薄壁锐缘孔来模拟管线渗漏,建立了管线渗漏模型,对于埋深深度不超过1.5 m的地下管线,假设管线不能抵抗周围土层的移动;文献[7]在弹性地基梁理论的基础上,推导了在隧道施工条件下管线弯矩的解析表达式;文献[8]利用连续弹性介质理论推导出管道位移和弯矩的表达式,并提出了管-土相对刚度的评估公式;文献[9]以沈阳地铁隧道为研究对象,应用FLAC3D计算软件模拟复杂条件下浅埋暗挖大跨度隧道引起的地表沉降变形特征,结果表明,模拟数据与现场监测数据具有较好的拟合性,利用数值分析方法预测大跨度隧道施工期地表沉降是可靠的;文献[10-11]利用ANSYS软件建立了隧道支护结构-土体-地下管线耦合作用的三维有限元分析模型,计算垂直于隧道方向地下管线的沉降,并对地下管线的安全性进行了预测,利用有限单元法分析隧道施工对邻近管线内力和位移的影响,指出隧道施工对管线的扰动程度与地层损失率有关;文献[12]采用弹性地基梁理论与管线-土-盾构相互耦合FLAC3D数值方法,分析了盾构隧道施工对邻近地下管线的影响,并与实测结果对比,发现弹性地基梁法可用于估算管线的最大变形,FLAC3D数值方法可较准确模拟盾构隧道对管线的影响;文献[13]建立结构-地层-管线三维弹塑性数值模型,得到管-土相对刚度小于0.18时,管线与土体沉降差小于5%,管-土相对刚度在2.8～7.2之间,地表与管线沉降相差小于5%,即地表沉降值可以作为管道沉降值;文献[14]建立了满足盾构隧道刚度要求的模型,可以实现局部节理渗水,其研究结果表明,渗水导致的孔隙水压力下降越明显,地表与隧道沉降越显著;文献[15]以某地铁盾构隧道的实测地面沉降数据为基础,详细分析了开挖过程中和开挖后的沉降规律。

本文采用室内模型试验,研究了地铁施工中管线渗漏对管线、地层及隧道管片造成的影响,分析盾构施工与管线渗漏作用对管线与地表沉降和隧道管片内力变化规律的影响。

1 模型概况

1.1 相似比

制作试验模型时要求模型的尺寸满足几何相似比,模型材料的重度和强度等近似满足重度相似比和强度相似比,开挖模拟时按照时间相似比确定开挖速度、支护时间、左右开挖间隔、应力和沉降的监测间隔和整个模拟试验的时间。根据相似原理确定试验参数相似比,见表1所列。

表1 模型相似比

1.2 模型试验箱

本次试验中,制作了长2.5 m、高1.0 m、宽0.6 m的模型试验箱,如图1所示。模型试验箱由角钢焊接制成箱体的框架,前后侧边界均用厚25 mm的透明有机玻璃进行约束,方便清晰地观测试验进行时箱体内部的情况。有机玻璃上预留直径0.12 m的孔洞为隧道所在位置,隧道模型底部离试验箱体底部距离为0.4 m。两侧采用密实厚木板制成,并在对应位置预留稍大于PVC管直径的圆孔,便于供水装置与管线联接。底板由密实厚木板制成,确保模型箱体具有足够的刚度,可有效控制箱体的变形。

图1 框架模型试验箱

1.3 砂土制备

砂土土样取自合肥典型砂土,基本参数见表2所列。使用砂雨法制作砂土模型,通过进行砂雨落高标定试验,最终取落高为1.0 m,落砂密度1.89 g/cm3,尽量与原始地层条件保持一致。

表2 砂性土体物理力学参数

2 试验概述

2.1 试验模型制作

试验前期进行了落砂试验研究,落砂石试验数据见表3所列。

表3 落砂试验数据

使用砂雨法制作砂土模型,如图2所示,步骤如下:将一定量砂样放入砂雨箱,悬挂至指定高度(高于箱体底部1 m),打开砂雨箱开关,使砂土均匀落下。每层落砂厚度控制在10 cm,一层完成后将砂雨箱提高10 cm进行下一层落砂,重复以上步骤直至填筑至管线埋深位置为止,待管线埋设好,最终制成高1.0 m的试验模型。

图2 试验模型箱照片

此次试验中,供水装置如图3所示,进水口可调节流量大小,用波纹软管将模型管线与供水管线联接,利用波纹软管轻、易伸缩的特点,最大程度减小管线的轴向拉力对管线沉降的影响。

图3 供水装置简图

2.2 测点布置

试验中的测量任务分为3个部分:① 通过在模型顶部固定百分表连接在管线上的抱箍沉降杆,对模型开挖过程中管线沉降进行监测,以便于总结盾构开挖对管线竖向位移的影响规律;② 通过在模型顶部固定百分表,监测模型试验开挖过程中地表沉降,总结盾构开挖对地表竖向位移的影响规律;③ 通过采用黏贴于隧道管片内壁电阻应变片测试管道微应变,分析盾构开挖和管线渗漏情况下隧道管片的应力-应变关系变化规律。

试验测点布置情形如图4所示,百分表布置情形如图5所示,隧道应变片布设情形如图6所示,应变片测点位置如图7所示。

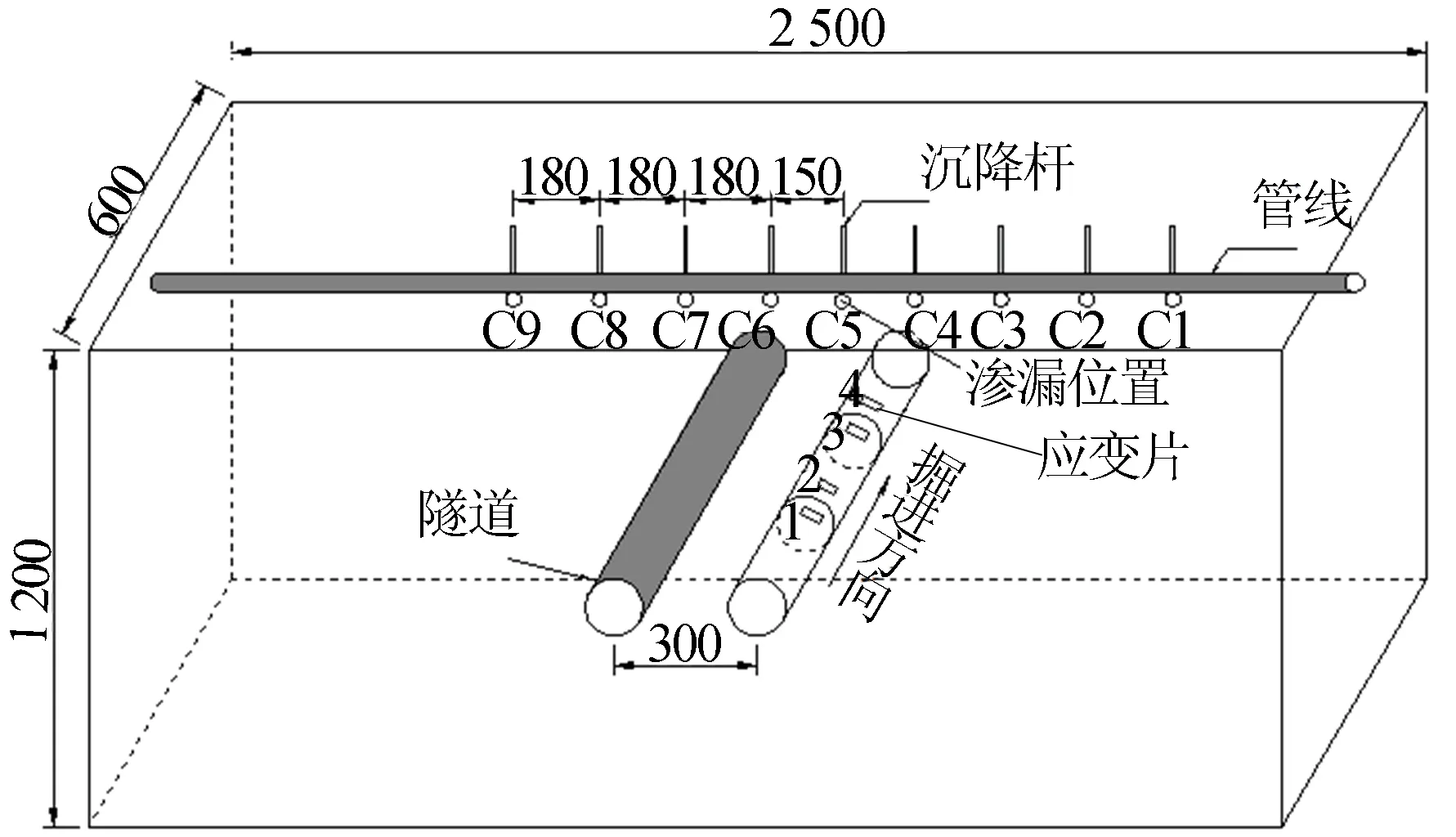
图4 试验测点布置情形

图5 百分表布置情形图6 隧道应变片布设情形图7 应变片测点位置

2.3 试验过程

模型砂样填充后,开始安放百分表,并将应变片的屏蔽测试导线连接至静态应变仪,在计算机外控状态下设定应变片、管线各项参数进行预测试。试验模型制作完成后,静置,监测管线沉降值和微应变,直至数值不再发生变化或者变化值很小(此时认为模型达到天然条件下的密实度),表明土体模型初始沉降状态已经完成,相当于初始地应力已经完全形成,可以进行开挖模拟试验,记录保存此时静态应变仪读数以及所有百分表的读数。为保证每组试验的均一性,每组试验模型制作完成后,静置时间保持一致。

隧道开挖共历时10.2 h,静置至微应变和沉降量数值不再发生变化或者变化值很小,此时,管线渗漏,渗漏水压力约为0.3 MPa。试验中,每隔15 min左右观察1次隧道拱顶的情况,当管线不再产生渗漏时,隧道拱顶拼接缝也能看到有些许渗水。

在试验结束后,取模型砂土样,得出此时砂土密度,并拆开模型观察,也能明显看到管线渗漏处至隧道拱顶范围内的砂土含水明显较高于周围砂土,最终渗漏水范围可确定为至隧道拱顶位置。

对管线沉降值、隧道应变值及地表沉降值进行连续监测,得到大量的试验数据,通过对数据从不同的侧重点进行整理,可以得到管线垂直位移的变化规律,以及盾构开挖条件下管线破坏后地表沉降和隧道应变规律。

3 试验结果分析

将试验开始记为0 h,0～18.2 h记为开挖稳定阶段,18.2～19.2 h记为渗漏第1阶段,19.2～20.2 h记为渗漏第2阶段,20.2～34.2 h记为渗漏第3阶段,管线、土体最终沉降至稳定状态。

3.1 管线整体沉降随时间变化规律

隧道开挖完成后,待到管线沉降趋于稳定,管线通水并发生渗漏,此时再监测管线沉降变化,隧道出现明显渗水后,关闭水源。在渗漏第1阶段,由于渗漏产生了渗透力,地层的应力进行重新分布,造成地表沉降,在管-土相互作用下,管线沉降也缓慢增大;在渗漏第2阶段,管线沉降明显加快,这是由于随着渗漏量增加,地表沉降加速,此时又带动管线沉降,造成此阶段管线沉降量明显变大;在渗漏第3阶段,管线沉降量逐渐减小,最终沉降趋于稳定,不再产生变化。

渗漏阶段管线沉降曲线如图8所示。

图8 渗漏阶段管线沉降曲线

中心沉降点渗漏阶段管线沉降结果见表4所列。渗漏第1阶段、第2阶段造成的沉降值较大,占总沉降量的16.66%;管线渗漏的水体对砂土的渗透力作用导致局部土体发生位移,在管-土相互作用下,管线沉降值增加,渗漏阶段管线沉降值占总沉降的24.76%。管线沉降各阶段最终稳定曲线表明,管线在这种情形下的沉降类似于两端简支、其上均布荷载的简支梁。

表4 中心沉降点渗漏阶段管线沉降结果

3.2 管线测点沉降随时间变化规律

从试验模型的隧道开挖,经过34.2 h的连续监测,获得了大量的试验数据,并经过整理研究管线的垂直位移变化。选取管线测点C3、C4、C5、C6、C7为研究对象,分析管线竖向位移随时间沉降变化规律,监测结果如图9所示。从图9可以看出:

图9 渗漏阶段管线沉降随时间变化曲线

(1) 在渗漏第1阶段,由于渗漏产生了渗透力,地层的应力进行重新分布,产生沉降,造成此阶段管线沉降增加,且沉降较大;在渗漏第2阶段,管线沉降速率明显增大,这是由于地层运动作用,引起管线产生附加变形和附加应力,导致管线受损且渗漏量增加,渗漏水又促使地表沉降速率加快,从而导致管线沉降速率加快;在渗漏第3阶段,隧道内出现明显渗水后,关闭水源,管线沉降逐渐趋于稳定,最终沉降不再发生变化。

(2) 管线竖向最大变形位于隧道轴线正上方,其次是中间,充分说明了隧道开挖和管线渗漏对隧道正上方土层扰动最大,地层损失最大。

(3) 距开挖隧道轴线的水平距离越远,沉降越小,表明渗漏影响范围有一定距离。

3.3 地表沉降规律对比

渗漏阶段地表沉降曲线如图10所示。由图10可知,隧道地表沉降槽曲线大致呈典型正态分布,宽度和深度较大,管线渗漏后的“沉降槽”也对称。

图10 渗漏阶段地表沉降曲线

在渗漏第1阶段,管线渗漏水对砂土产生了渗透力,地层的应力进行重新分布,地层开始沉降;在渗漏第2阶段,地表沉降明显加快,这是由于随着渗漏量的增加,造成局部砂土应力场和位移场变化加快,地表沉降加速;在渗漏第3阶段,管线沉降量逐渐减小,最终沉降趋于稳定,不再发生变化。管线渗漏造成的沉降值较大,这是由于管线渗漏的水体对砂土的渗透力作用,导致局部土体发生位移,沉降值变大。在砂土每个阶段的最终稳定性曲线中,地表沉降曲线通常是具有较大宽度和深度的典型正态分布。

在开挖稳定阶段和渗漏各阶段的时间段内,地表中心沉降点产生的沉降值见表5所列。由表5可知:

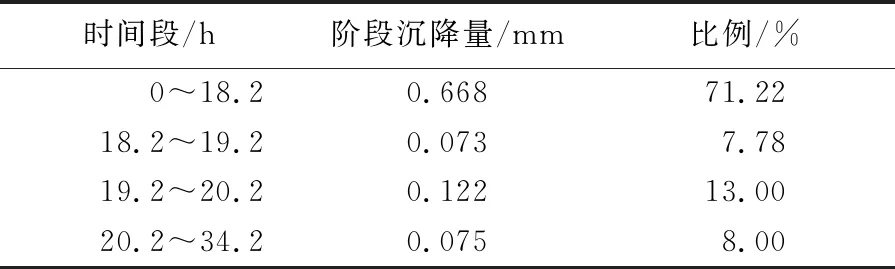
表5 中心沉降点渗漏阶段地表沉降结果

(1) 管线渗漏造成的地表沉降占总沉降的28.78%,前期的沉降是由于隧道直接开挖扰动土体所致的,后期的沉降则是管线渗漏水产生的渗透力造成的,导致土体应力场和位移场重新调整。同时,隧道盾构施工期间引起的沉降比较有限,大部分沉降是在开挖阶段完成产生的,但渗漏造成的地表沉降进一步增大,增加了地表沉降过大造成地表塌陷的危险。

(2) 渗漏第2阶段产生的沉降比第1阶段要大,表明随着渗漏时间的推移,更多的渗漏水渗入砂土,地层的应力变化加快,地表沉降进一步扩大。最后,渗流场趋于稳定,故渗漏第3阶段的沉降值较小。

3.4 隧道应变各阶段变化规律

隧道开挖过程中,对隧道管片应变进行实时测量。由于开挖引起地层损失导致地表沉降,使管片承受应力,并产生变形和附加应力。为了简化对模型变化规律分析,选取隧道衬护顶部的4个应变片测点进行分析,整个试验过程为单侧隧道开挖至静置稳定,时间为0～34.2 h。弯曲应力历时曲线如图11所示。

图11 隧道管片应力变化历时曲线

从图11可以看出:

(1) 测点1、测点2的应力变化类似,测点3、测点4的应力变化类似;靠近测点1、测点2侧先进行隧道开挖,故这2处测得的应力比测点3、测点4处的变化速率要快。

(2) 在开挖完成静置9 h,待到应力稳定后,管线发生渗漏,此时隧道顶部应力随时间增加开始增加;最终隧道顶部的微应变趋于稳定。

(3) 在完成隧道开挖时,应力不发生改变,此时测点1～测点4的应力分别为3.435、3.435、3.225、3.270 kPa;经过连续34 h监测,最终4个测点的应力变化趋于稳定,其应力值也趋于近似,此时测点1～测点4的最终应力分别为4.845、4.875、4.650、4.740 kPa。管线渗漏造成的隧道管片应力增量占最终应力的30%左右。

由此可以看出,管线发生渗漏时,隧道管片承受的应力要远大于开挖稳定后的应力,可能会出现管片环缝开量过大而漏水、漏砂或者管片纵向受拉破坏,对整个盾构施工造成较大的损失。

管线渗漏,水体进入砂土,在逐渐下渗过程中,渗漏产生了渗透力,地层应力重新分布,渗漏产生地表沉降,造成此阶段沉降速率加快,此时隧道顶部承受的压力变大。随着地表沉降变化,隧道应变逐渐增大,最终隧道应变趋于稳定。隧道周围地层在管线渗漏作用下产生不均匀沉降,地层表面的不均匀沉降逐级传递至隧道,所传递下来的压力会导致隧道顶部因受力而产生安全问题,因此必须加大对地铁隧道的保护力度。