基于灰色理论掺风积沙自密实混凝土强度分析与预测∗
2021-05-31邓焙元
李 佳,刘 清†,邓焙元,韩 通
(1. 新疆大学 建筑工程学院,新疆建筑结构与抗震重点实验室, 新疆 乌鲁木齐830047;2. 乌鲁木齐市政府投资城市基础设施建设中心, 新疆 乌鲁木齐830092)
0 引言
自密实混凝土是指在浇筑过程中免振捣,仅依靠重力就可流动并充满模板,能够自然流平密实,并且具有不离析、不泌水和分布均匀的优质混凝土[1]. 学者们对自密实混凝土的强度及其主要影响因素开展了研究[2−6],JUNG S H、CELIK、YANG S T等探究了不同掺合料取代率下养护龄期长短对自密实混凝土抗压强度、弹性模量等的影响[7−9],但这些研究需要进行大量系统的试验. 在多因素多水平试验中采用正交试验的科学方法不仅能够大量减少试验次数,而且可以分析各因素对实验对象影响的主次顺序并进行相关评价以提高试验的效率[10]. 在混凝土领域,正交试验方法多应用在混凝土配合比设计及力学性能影响因素分析方面[11−13],试验数据处理多采用线性回归方程进行分析与预测,但线性回归模型要求数据具有一定线性相关性,且建模方法单一,如梁凯等通过设计机制砂混凝土正交试验建立线性回归模型,研究机制砂掺量变化与机制砂自密实混凝土抗压强度之间的线性关系与规律[14]. 灰色系统模型则对数据无特殊要求,每种类型数据皆有对应的建模方法且可通过优化建模方法提高模型预测准确性[15,16].
灰色系统理论是一种贫数据处理方法[17],在有限的数据信息情况下对系统演化规律、数据内部变化趋势进行准确预判. 目前,灰色理论在混凝土领域的应用以单变量灰色模型预测最为普遍[18,19]. 多变量灰色模型则多用于经济运输及粮食产量预测等方面[20,21]. 而关于灰色系统理论结合正交试验运用于多因素自密实混凝土强度预测的研究还不多. 本文采用《混凝土物理力学性能试验方法标准》中所述的试验方法[22],基于正交试验数据运用灰色系统理论方法建立多变量灰色系统预测模型,探究各因素水平变化与C30掺风积沙自密实混凝土强度变化之间的联系与规律,通过灰色预测模型预测新配合比下掺风积沙自密实混凝土强度数据. 在正交试验的基础上,结合灰色理论分析各因素水平变化时C30掺风积沙自密实混凝土强度变化的规律与趋势,为C30掺风积沙自密实混凝土试验设计与现场施工提供依据和理论指导.
1 掺风积沙自密实混凝土正交试验设计及强度试验
1.1 正交试验设计
正交试验方法是一种经过大量试验总结并验证可行的科学试验设计方法,具有整齐可比性和均匀分散性的特点,并且试验结果也不会因为次数少而降低数据代表性及可靠性[23]. 可解决在多因素多水平条件下自密实混凝土试验不能一一遍历的问题.本文根据自密实混凝土强度影响因素并结合新疆风积沙与粉煤灰原材料充沛的特点,采用L16(45)正交试验设计表,考核指标为掺风积沙自密实混凝土7 d,28 d龄期下立方体抗压强度及28 d龄期下劈裂抗拉强度,对风积沙取代率、砂率、水胶比、颗粒级配、粉煤灰掺量五因素的强度变化规律进行分析. 各因素与水平设计情况见表1,试验配合比详见表2.

表1 因素水平表Tab 1 Factor level table

表2 试验配合比Tab 2 Mix proportion
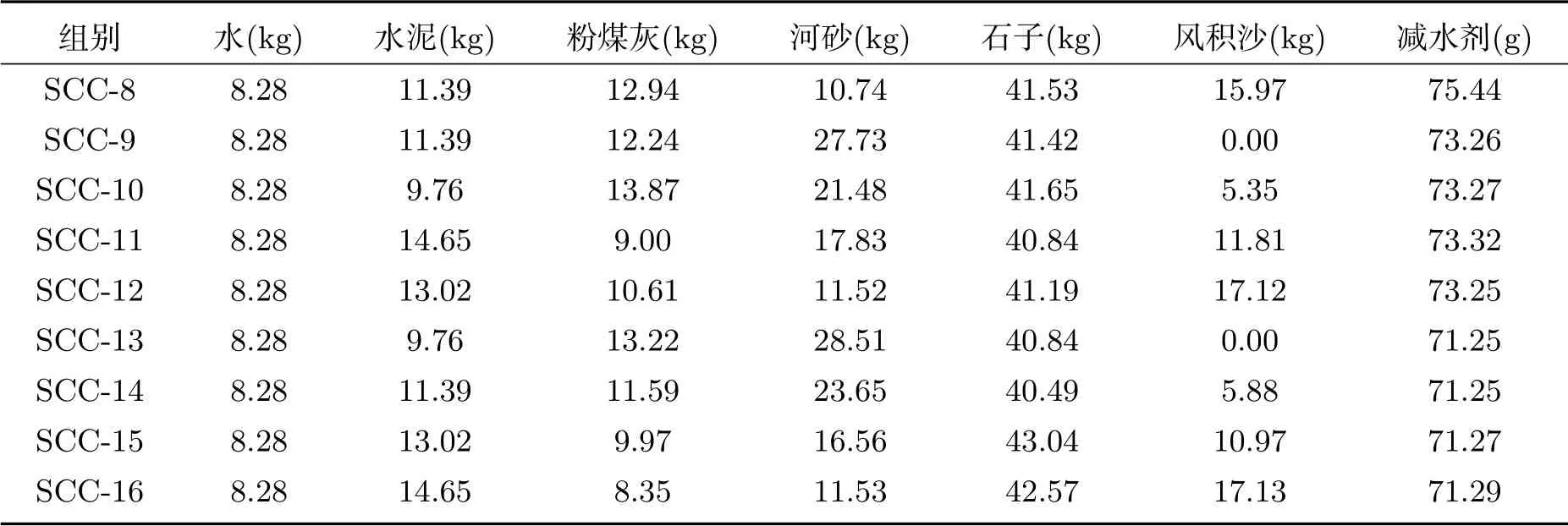
续表2
1.2 试验方法
本文掺风积沙自密实混凝土抗压强度与劈裂抗拉强度测试方法依据国家标准《混凝土物理力学性能试验方法标准》中规定的测试方法进行[22],配制试件尺寸为150 mm×150 mm×150 mm的掺风积沙自密实混凝土试件,制作完成后按标准养护程序分别养护至7 d龄期和28 d龄期后在新疆大学结构力学试验室进行抗压强度与劈裂抗拉强度测试,试验及测试过程见图1. 其中混凝土配合比编号SCC表示自密实混凝土.

图1 试验及测试过程Fig 1 Test and test procedure
1.3 正交试验结果
正交试验中各组配合比下掺风积沙自密实混凝土试件在不同龄期时抗压强度与劈裂抗拉强度试验数据如表3所示,从正交试验结果可看出:各组试件均能够满足C30掺风积沙自密实混凝土设计强度要求;掺风积沙自密实混凝土抗压强度在7 d龄期下为28 d龄期下的54%~87%;28 d龄期下其抗压强度平均值较7 d龄期下增加了14.36 MPa,增长幅度达54.9%. 28 d龄期时立方体劈裂抗拉强度为抗压强度的7.08%~15.84%,符合自密实混凝土劈裂抗拉强度约是抗压强度10%的经验数据.

表3 掺风积沙自密实混凝土正交试验结果Tab 3 Orthogonal test results of self-compacting concrete

续表3
1.4 力学性能影响因素分析
不同龄期掺风积沙自密实混凝土强度与各因素水平的关系如图2所示,图2中数据点为单因素不变时四组配合比下强度均值. 由图2可知,具有最佳抗压强度与劈裂抗拉强度的各因素水平分别为:水胶比0.35,风积沙取代率0%,粉煤灰掺量10%,颗粒级配50%,砂率40%,在实际情况下,可根据实际情况与性能要求,选择配合比中具有最优力学性能的各影响因素水平配制掺风积沙自密实混凝土.

图2 抗压强度、劈裂抗拉强度与因素水平趋势图Fig 2 The horizontal trend chart of compressive strength, splitting tensile strength and factor
1.4.1 水胶比因素分析
由图2(a)可知,掺风积沙自密实混凝土早期抗压强度与中期抗压强度对水胶比变化时表现出的强度曲线趋势有所差异. 7 d龄期下立方体抗压强度最大值为28.85 MPa,在水胶比等于0.34时获得,当水胶比增大至0.35时其抗压强度达到最小值24.18 MPa,下降了16.2%;28 d龄期下最大值为43.32 MPa,在水胶比等于0.35时获得,当水胶比减小至0.34时其抗压强度达到最小值38.96 MPa,下降了10.1%. 这是因为自密实混凝土的早期强度主要由水泥水化反应生成胶凝材料粘结骨料与砂浆提供,水化反应的同时生成大量氢氧化钙等伴生化合物与部分粉煤灰填充在因水化反应而产生的孔隙中,使其产生紧致密实的效果,此时在只有水泥水化反应提供胶凝材料的情况下达到最佳抗压强度的水胶比为0.34;在28 d龄期时水泥水化反应已接近尾声,并产生大量水化产物氢氧化钙,结合混凝土孔隙和微裂缝中的游离水分与粉煤灰产生剧烈的二次水化反应,产生二次凝胶粘结在骨料与砂浆之间,使得掺风积沙自密实混凝土粘结面的粘结强度增强,表现为其抗压强度增大. 在水胶比为0.35时,抗压强度取得最大值,表示在此数值下已充分满足两次水化反应所需用水量和胶凝材料,在其余参数不变的情况下增大或减小水胶比均会降低掺风积沙自密实混凝土抗压强度值.其劈裂抗压强度随着水胶比的增大表现为缓慢下降的趋势,但整体下降幅度在17%以内,说明水胶比的变化对掺风积沙自密实混凝土劈裂抗拉强度影响不大.
1.4.2 风积沙取代率因素分析
由图2(b)可知,随着风积沙取代率的增大,掺风积沙自密实混凝土早期强度和后期强度均呈下降趋势,7d龄期下立方体抗压强度最大值为30.39 MPa,在风积沙取代率等于0%时获得,当风积沙取代率增大至60%时,其抗压强度达到最小值22.62 MPa,下降幅度达25.6%;28 d龄期下其抗压强度最大值为44.49 MPa,在风积沙取代率等于0%时获得,当风积沙取代率增大至60%时,其抗压强度达到最小值35.76 MPa,下降幅度为19.62%. 由此可知风积沙取代率的变化对掺风积沙自密实混凝土抗压强度的影响较水胶比变化时更为显著.这主要是在水泥第一阶段水化反应中,风积沙只发挥微积料的作用而并不参与水化反应,随着风积沙取代率的增大(天然河砂用量减少),因风积沙形状较天然河砂圆润,表面粗糙度较小,使得胶凝材料在风积沙表面附着的粘结力有一定幅度减弱,故在7 d龄期下表现为掺风积沙自密实混凝土抗压强度持续降低;在28 d龄期下,风积沙颗粒在填充了自密实混凝土内部空隙的同时,也充分的参与水化,增加了粘结面的粘结强度,因此强度的下降幅度有所减少;随着风积沙取代率的增大,其劈裂抗拉强度逐渐减小,峰值与最小值之间下降幅度为20%,较水胶比增大时的下降幅度大,说明风积沙取代率的变化对掺风积沙自密实混凝土劈裂抗拉强度的影响更为显著.
1.4.3 粉煤灰掺量因素分析
由图2(c)可知,掺风积沙自密实混凝土早期强度与中期强度对粉煤灰掺量的变化所表现出的强度变化趋势并不完全相同. 随着粉煤灰掺量的增大,7 d龄期时其抗压强度呈持续下降的趋势,在粉煤灰掺量为10%时其抗压强度取得最大值29.89 MPa,当粉煤灰掺量继续增大至40%时,其抗压强度取得最小值23.48 MPa;下降幅度为21.44%;28 d龄期时其抗压强度先大幅度下降后又缓慢上升,在粉煤灰掺量为10%时其抗压强度取得峰值45.31 MPa,粉煤灰掺量为20%时其抗压强度取得最小值36.81 MPa,总体下降幅度为18.75%. 这主要是7 d龄期时随粉煤灰掺量的增加,水灰比下降,水泥砂浆粘稠度增加,游离水分流动互换受阻,其保水保湿作用亦无法满足全部水泥水化反应所需用水量. 在早期强度中随着粉煤灰掺量的加大,水泥水化反应减弱,因掺风积沙自密实混凝土早期抗压强度仅由水泥水化反应产生的胶凝材料提供,故表现为抗压强度值的持续降低;28 d龄期时由于粉煤灰掺量的突然增加导致水灰比下降,表现为掺风积沙自密实混凝土抗压强度的大幅度下降,由于水泥用量减少导致水胶比相对增大使得第二阶段水化反应充分进行,同时剩余未参与水化反应的大部分粉煤灰充分发挥微积料效应,且混凝土水化反应会产生一定的塑性收缩,综合作用下使得掺风积沙自密实混凝土结构更密实,而表现为其抗压强度的缓慢上升. 28 d龄期时劈裂抗拉强度呈缓慢下降趋势,总体下降幅度为20.17%,较水胶比变化时的下降幅度大,也是由于水化反应不充分、粘结面强度减弱导致,说明粉煤灰掺量变化对掺风积沙自密实混凝土劈裂抗拉强度的影响比水胶比变化时的影响显著.
1.4.4 颗粒级配影响因素分析
由图2(d)可知,随着风积沙中粗颗粒(颗粒级配)含量的增加,掺风积沙自密实混凝土抗压强度曲线在7d龄期下,当颗粒级配由50%上升至70%时,其抗压强度由28.44 MPa减小至24.8 MPa,下降了12.8%,当颗粒级配由70%继续增大时其抗压强度曲线趋于平稳无波动;28 d龄期下其抗压强度最大值为46.05 MPa,出现在颗粒级配50%位置,颗粒级配增加至70%时,其抗压强度下降为38.22 MPa,当颗粒级配增大至80%时,出现第二峰值42.44 MPa,颗粒级配增大至90%时再次下降为35.31 MPa,强度曲线表现为上下波动的现象,但总体呈下降趋势,总体下降幅度为23.3%. 这主要是随着粗颗粒含量的增加(细颗粒含量减少),风积沙颗粒与胶凝材料的粘结总表面积减少,粘结力强度减弱导致相对薄弱界面增多,故7 d龄期抗压强度整体上表现为先下降后平稳的趋势;28 d龄期时立方体抗压强度在粗颗粒含量80%处出现一个小波峰,这是由于风积沙中细颗粒含量的减少造成的. 由于粗细颗粒占比的变化,使得水泥水化反应、粉煤灰的二次水化反应充分进行,导致抗压强度的暂时升高,除此之外,风积沙中粗颗粒含量的增加使得掺风积沙自密实混凝土粘结面的粘结力降低,故表现为其抗压强度低于粗颗粒含量为50%的值. 28 d龄期下随着风积沙中粗颗粒含量由50%增大至70%的过程中,粗颗粒骨料间的机械咬合力增大幅度大于表面积减小导致的粘结力减小幅度,表现为劈裂抗拉强度增大,增大幅度为17.23%;当颗粒级配继续增大至80%时,其劈裂抗拉强度减小为3.74 MPa,总体下降幅度为25.05%,由此说明当风积沙中粗颗粒含量为70%时,骨料间的机械咬合力和粘结面的粘结力互补效应同时达到最大值. 不难得出,风积沙中粗颗粒的含量变化对掺风积沙自密实混凝土抗压强度和劈裂抗拉强度的影响较其他因素的变化具有更为显著的影响.
1.4.5 砂率影响因素分析
由图2(e)可知,在7 d与28 d龄期下,掺风积沙自密实混凝土抗压强度随砂率增大,两条抗压强度曲线变化趋势大体一致. 7 d龄期下,随着砂率由39%增大至40%,掺风积沙自密实混凝土抗压强度由24.69 MPa增大至30.33 MPa,取得峰值,当砂率由40%继续增大至41%时,其抗压强度表现为减小趋势,下降幅度为18.66%,砂率继续增大至42%时,其抗压强度趋于平稳,其抗压强度峰值与最小值之差为5.67 MPa;28 d龄期下,当砂率由39%增大至40%,其抗压强度由14.72 MPa增大至44.03 MPa,砂率增大至41%时,其抗压强度下降为36.49MPa,砂率为42%时,抗压强度为39.77 MPa,其抗压强度曲线变化呈波动现象,抗压强度最小值较峰值下降了17.1%. 这主要是砂率的增加增大了掺风积沙自密实混凝土中砂石与水化反应产物胶凝材料的接触面积,增大了粘结面的受力面积,风积沙颗粒的累积效应导致掺风积沙自密实混凝土抗压强度曲线呈现增大趋势;当砂率由40%继续增大时,掺风积沙自密实混凝土浆体粘稠度增加使其流动性减弱,阻挡了游离水分的流通及均匀分布,从而导致其两阶段的水化反应进行不充分,总体生成的胶凝材料量减少,导致掺风积沙自密实混凝土抗压强度降低. 7 d龄期下砂率由40%继续增大时其抗压强度持续减小,而28 d龄期下当砂率增大为42%时其抗压强度又出现第二峰值,说明第二阶段水化反应充分进行导致了抗压强度的再次增大,这主要是其他因素如水胶比、风积沙取代率的变化带来的影响. 28 d龄期下劈裂抗拉强度随砂率的增大表现为持续而缓慢的下降,下降幅度为23.03%,这是由于掺风积沙自密实混凝土中石子为粗骨料,砂率增大的同时掺风积沙自密实混凝土中石子含量相应减少,粗骨料间的机械咬合力减弱,虽然同时粘结面强度增强,但减弱幅度大于增强幅度,故表现为劈裂抗拉强度逐渐减弱.
1.5 多因素综合分析
综合上述强度分析,在28 d龄期下,当水胶比因素水平为0.35时,掺风积沙自密实混凝土抗压强度取得峰值43.32 MPa,当水胶比增大或减小范围在0.1以内时,其抗压强度均会下降10%左右;当风积沙取代率为0%时,掺风积沙自密实混凝土抗压强度取得最大值44.49 MPa,风积沙取代率每增大20%时,其抗压强度均匀且持续下降8.3%左右;当粉煤灰掺量为10%时,掺风积沙自密实混凝土抗压强度取得最大值45.31 MPa,粉煤灰掺量为20%时取得最小值36.8 MPa,当粉煤灰掺量由20%开始每增大10%时,其抗压强度会缓慢均匀上升6.2%左右;当颗粒级配中粗颗粒含量为50%时,掺风积沙自密实混凝土抗压强度取得最大值46.05 MPa,颗粒级配每增大10%时,其抗压强度呈现规律性波动变化,但总体呈下降趋势,波动幅度在11%左右;当砂率为40%时,掺风积沙自密实混凝土抗压强度取得最大值44.03 MPa,当砂率增大或减小1%时,会不同程度降低其抗压强度值,下降幅度范围在5.2%~17%之间. 这是因为在7 d龄期下掺风积沙自密实混凝土抗压强度主要由水泥第一阶段水化作用产生胶凝材料提供,粉煤灰只发挥微积料的作用填充在掺风积沙自密实混凝土中,因水泥水化作用而产生的孔隙并不参与水化反应,对早期强度增益不明显. 随着龄期增长至28 d时,粉煤灰的水化活性缓慢发挥作用,并结合其保水保湿作用解锁孔隙中的游离水分与氢氧化钙发生剧烈的二次水化反应,生成的二次胶凝材料使得掺风积沙自密实混凝土的强度稳定性有所提高,由于其在水化反应时伴随着塑性收缩,同时未反应的粉煤灰继续填充在因失水而产生的孔隙中,使得掺风积沙自密实混凝土结构更加致密,表现为其抗压强度再次增大.水胶比、风积沙取代率、粉煤灰掺量是其抗压强度的主要影响因素,控制并选取最佳的上述材料参数可提高掺风积沙自密实混凝土抗压强度.劈裂抗拉强度的大小由掺风积沙自密实混凝土中粗骨料间的机械咬合力大小和粘结面的粘结强度共同决定;同时当其它参数不变时,选取合适的砂率亦能增强掺风积沙自密实混凝土的力学性能.在本次试验参数设定下,综合各因素分析且仅考虑其力学性能情况下,取因素水平为水胶比0.35、风积沙取代率0%、粉煤灰掺量10%、颗粒级配50%、砂率40%时可配制出具有最优力学性能的掺风积沙自密实混凝土.
2 掺风积沙自密实混凝土强度预测方法研究
2.1 多变量灰色系统模型
2.1.1 传统GM(1,N)模型
(1)设原始数据对n个材料配合比方案混凝土抗压强度有n个检测量,并有N个材料配合比指标序列的资料即

(2)求其相应的一次累加生成序列(AGO)

(3)(k)为(k)的紧邻均值生成序列

(4)建立传统GM(1,N)模型:

(5)求GM(1,N)的白化微分方程

(6)参数a称为模型发展系数,反映的发展态势,bi称为驱动系数,是从背景值挖掘出来的数据,它反映数据变化的关系[17]. 用最小二乘法解微分方程得其最优参数列,最小二乘估计满足
(7)时间响应式(白化方程的解)

(8)累减还原求特征变量拟合值与预测值

由时间响应式可以看出,发展系数a和驱动系数b是影响模型准确性的关键因素,数据序列中初始迭代基值对其也有一定影响,对传统GM(1,N)模型计算过程进行分析,通过优化发展系数a和驱动项b的求解方法并在模型中加入常数建立灰色优化模型.
2.1.2 灰色优化MGM(1,N)模型
(1)由上述方法求解一次累加序列,建立MGM(1,N)模型(灰色优化模型),其中u为灰作用量,ω为延时缓冲算子

(2)求延时缓冲序列

(3)求解MGM(1,N)的白化微分方程

(4)u为灰作用量. 用最小二乘法解微分方程得其最优参数列

(5)求解得时间响应式

(6)累减还原求特征变量拟合值与预测值

2.2 模型精度检验
2.2.1 残差检验[24]
(1)模型预测误差

(2)相对误差

∆k的值越小越好,一般要求∆k<15% ,当不符合此要求时,则认为此问题不适合使用多变量灰色系统预测模型.
2.2.2 关联度检测
计算原始数据与模型拟合预测数据的关联度.
(1)求差序列

(3)求关联系数

式中:ξ称为分辨系数,范围为0~1,一般取0.5.
(4)求原始序列与预测序列灰色绝对关联度

通过计算模型预测序列与原始数据序列之间的灰色绝对关联度,判别模型预测精度是否满足实际需求.当γ1i>0.6时,则说明以上方法所建立的灰色预测模型可以达到满意的效果,且预测数据具有较高的可靠性.
2.2.3 后验差检验
(1)求试验数据序列的均值与方差

(2)求预测序列的残差均值与方差

(3)称C=S2/S1为后验差比值. 表4给出了模型精度的判断标准[24].

表4 灰色模型精度判断标准Tab 4 Grey model accuracy criterion
2.3 灰色模型建立方法
正交试验数据与模型预测结果比较如表4所示. 其中试验数据中第一组28 d龄期下掺风积沙自密实混凝土抗压强度达55.49 MPa,偏离设计值80%以上,认为此数据对模型预测精度具有较大影响故舍弃不用. 采用剩余前十二组掺风积沙自密实混凝土抗压强度与劈裂抗拉强度数据,并应用上述建模方法建立传统GM(1,6)灰色模型与优化MGM(1,6)模型,最后三组掺风积沙自密实混凝土配合比与强度数据用于与预测值作对比,对两种灰色预测模型的预测精度及预测数据可靠度等进行评价,并检验模型预测准确性能否满足实际需要. 将各组配合比数据分别带入传统多变量灰色模型与灰色优化模型,得到灰色系统模型拟合值与预测值.
2.3.1 灰色系统模型数据拟合预测误差对比
由上述掺风积沙自密实混凝土正交试验数据,利用灰色理论建模方法,7 d抗压强度与五因素之间灰色传统模型见式(21);28 d抗压强度与五因素之间灰色传统模型见式(22);28 d劈裂抗拉强度与五因素之间灰色传统模型见式(23). 将五因素配合比不同水平的组合序列(即表3中配合比序列)代入模型可得强度预测一次累加序列,经式(7)累减还原计算后可得强度预测值. 表3中同种因素由上至下构成因素水平序列,序列编号由左至右依次为X2,X3,X4,X5,X6;同理可得各强度序列.


通过优化参数求解方法后,7 d抗压强度与五因素之间灰色优化模型见式(24);28 d抗压强度与五因素之间灰色优化模型见式(25);28 d劈裂抗拉强度与五因素之间灰色优化模型见式(26). 将表3中配合比序列以式(3)求得紧邻均值序列后代入优化模型可得强度预测一次累加序列,经式(13)累减还原计算后可得强度预测值. 模型预测数据与试验数据见表5.
表5中采用SCC-2到SCC-13共12组数据建立灰色系统模型,SCC-14到SCC-16三组为新配合比数据带入模型所得掺风积沙自密实混凝土强度预测值,用于验证五因素任意水平下灰色系统模型强度预测精度是否符合要求,并计算模型预测值与试验数据的平均相对误差. 由前12组拟合数据对比可得出:在7 d龄期下传统多变量模型抗压强度平均相对误差为15.85%,灰色优化模型抗压强度平均相对误差为9.25%,误差较传统模型降低了6.6%;在28 d龄期下传统多变量模型抗压强度平均相对误差为8.54%,灰色优化模型抗压强度平均相对误差为6.7%,误差较传统模型降低了1.84%;在28 d龄期下传统多变量灰色模型劈裂抗拉强度平均相对误差为14.18%,灰色优化模型劈裂抗拉强度平均相对误差为8.86%,误差较传统模型降低了5.32%. 以上均表明,在使用优化灰色系统模型参数计算方法后,掺风积沙自密实混凝土强度数据预测的平均相对误差均有较大程度的降低,即多变量灰色优化模型预测精度较传统模型有了很大的提高,预测数据具有更高的可信度和有效性. 对于本次试验设计参数,灰色优化模型可更为准确的表达掺风积沙自密实混凝土强度与各因素不同配合比的内在联系规律.
由后3组预测数据与实验数据对比可得出:在7 d龄期时,灰色传统模型对于SCC-14和SCC-15组的预测效果略优于灰色优化模型,灰色优化模型对于SCC-16组的预测效果优于灰色传统模型;在中期28 d龄期时,灰色传统模型无论是抗压强度还是劈裂抗拉强度仅表现出对SCC-14与SCC-15组有15%以内的预测相对误差,灰色优化模型则对于SCC-14、SCC-15、SCC-16组均有10%以内的预测相对误差,从预测组与试验数据对比情况可得,灰色优化模型相较于灰色传统模型具有更高的预测精度和时间有效性,可为试验设计等提供更多的参考依据.

表5 立方体强度灰色理论模型拟合预测结果Tab 5 The cube strength grey theory model fits the prediction results
由表5可得,序列预测长度和变量数据变化对灰色预测模型的预测有效性有显著影响,其中预测精度更高的灰色优化模型亦表现出SCC-14、SCC-15组具有10%以内的强度预测误差,而第三组预测值误差表现出增大的趋势.
2.3.2 模型误差分析
容易观察到在灰色传统模型和灰色优化模型拟合预测时均出现了个别预测相对误差在15%以上的现象,误差原因可能来自于:从试验前期看,试验时不排除人工因素(浇注不均匀、养护不当等)和本文未提及的其他环境因素,如温差、空气湿度等作用而出现个别掺风积沙自密实混凝土试件性能优于或劣于正常掺风积沙自密实混凝土的现象,如在建模中剔除的明显异常数据55.49 MPa,其余个别试块强度误差均在波动允许范围内,但此点对试验数据准确性及模型精度影响很小;试验过程中,试验室测试机器均至少有十几年工龄,在测量时偶尔会出现测量误差,但设备会及时检修消除出现误差的可能性,且试验数据本身具有一定离散性,反复测试下误差并不会太大(每个强度数据均是取三组测试的平均值). 综上所述,试验误差因素对于试验数据和灰色系统模型准确性无太大影响;从模型求解的计算表达式可看出,在模型计算时以原始序列初始值作为迭代基值并不一定符合事实,对于准确拟合试验数据和预测后期的变化规律具有较大影响;从模型本身看,灰色系统模型是依托于指数函数发展变化而来,而本文的研究数据在经过一次累加生成后依然不完全满足指数函数模型的数据特征,试验数据的一次累加序列亦具有一定的线性相关关系,也不完全满足线性相关性,故拟合预测数据中会出现个别数据具有较大误差的现象.
由上述分析可知,模型预测误差主要来源于灰色系统模型计算方法方面,针对以上可能的原因,提出拟解决办法:试验方面,可寻求条件更加优越的试验设施,减少非人为因素的干扰,学校试验室现已更新搅拌机设备(型号HC-HJS60),可基本消除设备老化带来的误差风险;模型方面,可以通过将序列中靠后的值作为迭代基值,可在一定程度上消除迭代基值对模型预测准确性的影响;仅应用3组以内新配合比进行强度预测会获得更高的预测精度,同时建立新陈代谢模型,把对数据规律贡献变小的旧数据去掉,并加入更能表达强度规律的新数据获得更为准确的预测数据,周而复始建立更能反映近期变化规律的新灰色系统模型进行预测,可获得预测精度更高且更加有借鉴价值的强度预测数据;在单变量GM (1,1)模型预测中结合线性回归模型建立灰色线性回归组合模型来解决灰色预测模型无法描述线性关系问题,因本文为多因素多水平的求解问题,此改进方法还有待进一步开发,在此不再赘述. 通过采用以上改进措施后将更有助于探索掺风积沙自密实混凝土各因素配合比与强度之间的规律与联系,为掺风积沙自密实混凝土试验设计与现场施工提供更多借鉴.
2.4 强度趋势图
为更加直观对比传统多变量灰色模型与灰色优化模型的预测性能,将实际的试验数据与两种模型的拟合值、预测值绘制成如图3所示的立方体强度预测趋势图.

图3 掺风积沙自密实混凝土立方体强度灰色模型拟合预测图Fig 3 The grey model of eolian sediment self-compacting concrete cube strength fit the prediction diagram
在图3中,横坐标表示参与模型计算的所有配合比组别,纵坐标表示通过建立灰色传统模型和灰色优化模型计算所得的7 d龄期和28 d龄期下抗压强度与28 d龄期劈裂抗拉强度拟合值、预测值,其中数据点为试验数据强度值、12组正交试验数据拟合值与3组新配合比下不同龄期立方体强度的灰色模型预测值. 在趋势图中,数据拟合预测折线图越靠近原始试验数据折线图则说明模型拟合预测精度越高. 由图3可知,灰色优化模型所得强度预测趋势图均表现出与试验数据更好的接近性,其在28 d龄期下对掺风积沙自密实混凝土抗压强度趋势预测表现出最优的接近性效果,说明对28 d龄期下抗压强度序列具有最高的预测精度. 灰色优化模型对掺风积沙自密实混凝土强度整体预测趋势的相似性均优于灰色传统模型,与试验值的实际偏差波动更小,更有利于试验数据的分析和指导施工,容易观察到多变量灰色优化模型具有更高的预测精度和可信度. 对图3中折线图接近性做定量分析,可得如下模型精度检验分析.
2.5 灰色优化模型精度检验
(1)残差检验
由表5可得,多变量灰色优化模型7 d龄期下掺风积沙自密实混凝土抗压强度预测平均相对误差为9.25%,28 d龄期下其抗压强度预测平均相对误差为6.7%, 28 d龄期下其劈裂抗拉强度预测平均相对误差为8.86%,均满足多变量灰色预测模型相对误差小于15%的要求,且精度达到二级,可用于指导掺风积沙自密实混凝土试验设计.
(2)关联度检验(ξ取0.6)

表6 关联度检验情况表Tab 6 Table of test of correlation degree
(3)后验差检验

表7 后验差检验情况表Tab 7 Condition table of posterior difference test
由表5、表6、表7模型精度检验可知,后验差检验指标为一级,平均相对误差检验指标为二级,关联度检验指标为三级,说明该模型是一个精度较优的预测模型,各指标均满足模型精度要求,可应用于数据预测及相关试验参考.
由模型精度检验可得,多变量灰色优化模型具有更高的预测精度和数据可靠性,能够更好的模拟强度曲线的趋势以及具有更好的模拟预测效果. 对于本次试验设计参数,灰色优化模型可更为准确的表达掺风积沙自密实混凝土各因素与立方体强度之间的规律与联系.
2.6 模型准确性进一步验证
灰色优化模型精度检验利用本次试验中其余强度数据对灰色系统模型预测精度进行验证对比,对此建模方法和灰色系统模型的准确性判断缺乏一定的说服力. 故在本节中引入曹佃雨所做的掺合料对C30再生粗骨料自密实混凝土简支梁受弯性能试验中的部分配合比试验数据[25],对本文建模方法和灰色模型预测精度进行进一步验证.
引入文献[25]中无掺加矿渣粉的三组配合比数据(因本文所设计试验中并未添加矿渣粉,原材料不同必然导致其力学性能表现有巨大差异)对灰色模型预测精度进行再次验证,试验配合比数据如表8所示. 在三组配合比中仅水泥用量和粉煤灰掺量有所变化,将配合比与本文因素表对应可得出水胶比与粉煤灰掺量变量及其相应强度数据如表9所示.

表8 试验配合比Tab 8 Mix proportion

表9 自密实混凝土试验测试结果Tab 9 Self-compacting concrete test results
将表9中因素配合比数据加入表2中已有配合比序列之后,代入灰色传统模型与灰色优化模型中,在模型中去掉无对应配合比数据的风积沙取代率、颗粒级配、砂率3个变量,并计算其相对误差如表10所示. 由表10可得模型预测结果平均相对误差最小为3.92%,且两种模型的平均相对误差均小于上文中五个因素变量的平均相对误差,对于多变量灰色系统预测模型而言,其变量个数越少,预测运算时的干扰因素就越少,则预测精度便会越高. 从表10中可看出优化算法后的多变量灰色优化模型强度预测精度明显优于传统多变量灰色模型,在7 d龄期下传统多变量模型抗压强度平均相对误差为14.23%,灰色优化模型抗压强度平均相对误差为5.76%,误差较传统模型降低了8.47%;在28 d龄期下传统多变量模型抗压强度平均相对误差为12.57%,灰色优化模型抗压强度平均相对误差为4.56%,误差较传统模型降低了8.01%;在28 d龄期下传统多变量灰色模型劈裂抗拉强度平均相对误差为10.5%,灰色优化模型劈裂抗拉强度平均相对误差为3.92%,误差较传统模型降低了6.58%;以上表明,灰色优化模型的预测精度与准确性均优于灰色传统模型,且预测精度可满足试验配合比设计需求.

表10 灰色系统模型强度预测结果对比Tab 10 Comparison of grey system model strength prediction results
2.7 预测结果
本文选取正交试验中十二组数据建立灰色预测模型,并对其进行新配合比下的自密实混凝土强度预测,预测结果表明灰色优化模型预测结果更为准确、精度更高. 新配合比下掺风积沙自密实混凝土立方体强度预测结果与实际试验数据更为接近. 在本次试验设定下,灰色优化模型更好的描述了掺风积沙自密实混凝土强度随材料配合比变化而变化的趋势和规律. 随着风积沙取代率与粉煤灰掺量的增大,粉煤灰二次水化反应生成胶凝材料的作用逐渐减弱,使混凝土抗压强度呈下降趋势;随着水胶比增大,水化反应因粉煤灰保水保湿作用先后充分进行,未参与反应的部分粉煤灰充分发挥其微积料效应填充在孔隙中,同时混凝土水化反应会产生一定的塑性收缩使得掺风积沙自密实混凝土内部结构更加致密,表现为抗压强度增大,试验结果与预测结果均表明在水胶比因素水平为0.35时掺风积沙自密实混凝土抗压强度达到最大值. 劈裂抗拉强度受各因素影响变化范围不尽相同,主要受粗骨料间的机械咬合力大小与混凝土内部粘结面粘结强度大小影响,在本次试验中砂率因素水平为40%,粉煤灰掺量水平为10%,掺风积沙自密实混凝土劈裂抗拉强度达到最大值.灰色优化模型能够更好的预测新配合比下掺风积沙自密实混凝土的抗压强度与劈裂抗拉强度,通过不断加入新数据去掉老数据,建立新陈代谢模型等方法能够提高模型预测精度,使之更加贴近自密实混凝土力学性能变化规律,反映混凝土强度随配合比变化的趋势,为试验设计、工程施工提供参考依据.
在上述分析中,掺风积沙自密实混凝土五种影响因素,每种因素取四水平,利用正交试验可得16组代表性试验结果,但每种因素不止四水平,在不同的工作环境下,需要强化突出其不同方面的力学性能,若需得到本文配合比之外的C30掺风积沙自密实混凝土强度值,一般需再次设计试验才能获得,既耗时费力且一般项目经费亦有限. 而利用上文建立的灰色优化模型可以求得五因素任意水平配合比下C30掺风积沙自密实混凝土强度值,且预测准确性在90%以上,本文仅基于C30掺风积沙自密实混凝土试验,但试验数据中有半数28 d抗压强度在40 MPa~48 MPa之间,故可认为灰色优化模型对于C30掺风积沙自密实混凝土强度范围(30 MPa~48 MPa)内预测数据可保持高精度.在实际应用中可在本文原序列基础上添加少量风积沙自密实混凝土配合比数据与强度数据,即可在保证精度的前提下扩大灰色优化模型预测范围,从而可为掺风积沙自密实混凝土在各种工况下的实际应用提供具有指导意义的高精度预测数据.
3 结论
本文通过设计掺风积沙自密实混凝土正交试验,研究其各影响因素对其强度的增强与减弱机理,并建立多变量灰色系统模型,得出以下结论:
(1)水化反应进行程度对掺风积沙自密实混凝土抗压强度具有重要影响. 水胶比影响第一阶段水化反应,粉煤灰掺量、风积沙取代率影响第二阶段水化反应的程度,因此在实际问题中选取具有最优力学性能指标的上述因素水平可显著提高掺风积沙自密实混凝土抗压强度;
(2)劈裂抗拉强度主要影响因素为粗骨料间的机械咬合力大小和粘结面的粘结强度,当颗粒级配与砂率增大,粗骨料的机械咬合力增强幅度大于粘结面强度减弱幅度,表现为增大趋势;继续增大时,粘结面强度减弱幅度大于机械咬合力增大幅度,表现为减小趋势;
(3)综合本次试验分析,当水胶比因素水平为0.35、风积沙取代率水平0%、粉煤灰掺量10%、颗粒级配(0.15 mm~0.3 mm)50%、砂率水平40%时可配制出具有最优力学性能指标的掺风积沙自密实混凝土. 可为充分利用新疆优势自然资源风积沙设计配置自密实混凝土提供指导;
(4)在掺风积沙自密实混凝土正交试验基础上运用灰色系统理论,建立多变量灰色系统模型并对算法优化得到灰色优化模型强度预测值,由模型精度检验分析可知多变量灰色优化模型预测具有更高的预测精度和数据可靠性. 对于探寻多因素下掺风积沙自密实混凝土强度变化规律具有一定实用价值;
(5)灰色优化模型可更为准确的表达掺风积沙自密实混凝土强度与各因素不同配合比的内在联系规律,且能更好的拟合强度曲线的变化趋势. 多变量灰色优化预测模型可以求得五因素任意水平配合比下掺风积沙自密实混凝土强度值,且预测准确性在90%以上,可为掺风积沙自密实混凝土在各种配合比工况下的实际应用提供具有指导意义的高精度预测数据.
