用“圆心线的方法”解决带电粒子在匀强磁场中的运动问题

摘 要：带电粒子在有界匀强磁场中做匀速圆周运动是比较常见的考题.本文通过提出“圆心线”的概念，进行了根据半径相等、在圆心线上找圆心的尝试，以便寻找一种便捷的、可操作性强的、通用的解题方法.

关键词：带电粒子;圆心线;圆心;临界

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）34-0090-02

收稿日期：2021-09-05

作者简介：李建海，男，河北省怀安人，本科，中学高级教师，从事高中物理教学研究.

带电粒子在有界匀强磁场中做匀速圆周运动的问题比较常见，是高考中的高频考点.该题型既能够考察学生物理建模的能力、还能够考察学生应用数学知识解决物理问题的能力.特别是与之结合的临界问题，难度往往较大.一些教参和文章中讨论的方法可操作性不强，本文就该类问题再做一些尝试.

一、试题的命制

关于带电粒子在匀强磁场中的运动的考题，可谓是常考常新，不管考题如何变化，大体可分为两类：一类是速度方向与某一特定边界夹角已知，即速度方向已知，但大小并不确定;一类是速度大小相等，方向分布在某一范围内.当然，从题目的命制来说，这只是两个大类，单纯给定这样的设定，其条件并不完备，常常需要再补充“粒子通过磁场中的某一点或与某一边界相垂直或相切”等条件，如图1，这样的组合就构成了形形色色的试题.

图1

二、现行方法评价

大多数教学参考书给出的解题方法如下：第一大类中，如果要求过某个点，相当于已知了弦，通过做弦中垂线和速度垂线交点，该交点即为圆心;如果轨迹与某一边界相切，通过做该边界与速度的角平分线，角平分线和速度垂线的交点即为圆心.不少文章还提出了“缩放圆”的方法.

对于第二大类，教学参考书中并没有给出相应的解题方法，不少文章提出了“动态圆”的方法.

这些方法其实叫做资源包更准确，看似能够解决相应的问题，但是并没有共性，一题一法，对于复习备考的学生来说，无疑是很大的负担.“缩放圆”和“动态圆”在具体解题中的操作性并不强，做角平分线耗时较长，与高考考场上快捷、可操作性强的需要相冲突.

三、该类问题的突破点

该类问题的突破点，归根到底就一个，那就是快速确定轨迹圆的圆心.两种题型，为了统一，可以提出“圆心线”的概念.圆心线即为一系列不确定圆的圆心的集合.第一大类中

速度垂线即为圆心线，如图2;第二大类中以入射点为圆心，粒子轨迹半径为半径的圆即为圆心线，如图3.如果速度分布在90°范围内，圆心线为1/4圆，如果速度分布在180°范围内，圆心线为半圆.

图2图3

有了圆心线的概念，这样在解决具体问题中只需根据半径相等的特征在“圆心线”上找出大致的圆心即可.这样做的效果是快捷、便于操作、通用性强，从而学生负担小.

第一大类中，过确定点A、与边界垂直和与边界相切找圆心的方法如图4所示.找圆心时把握两点，一是在圆心线上，二是半径相等.若要求过某一确定点，可以通過肉眼找一个大致的圆心，也可以做弦的中垂线，其实即使是做弦的中垂线，实际操作中也并非是用尺规作图，也是做了一个大致的中垂线，图4（a） ;若要求与某一边界相垂直，圆心为圆心线和该边界的交点，图4（b）;若要求与某一边界相切，根据半径相等这一特征，同时找切点和圆心，图4（c）.

图4

第二大类中，过确定点A、与边界垂直和与边界相切找圆心的方法如图5所示.方法与解决第一大类的方法一致.这样一来，“在圆心线上找圆心”便成了通用的方法，便于掌握.

图5

四、例题解析

如图6所示，在0≤x≤3a区域内存在与xOy平面垂直的匀强磁场，磁感应强度的大小为B.在t=0时刻，一位于坐标原点的粒子源在xOy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向夹角分布在0～180°范围内.已知沿y轴正方向发射的粒子在t=t0时刻刚好从磁场边界上P（3a，a）点离开磁场.求：

（1）粒子在磁场中做圆周运动的半径R及粒子的比荷q/m;

（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围;

（3）从粒子发射到全部粒子离开磁场所用的时间.

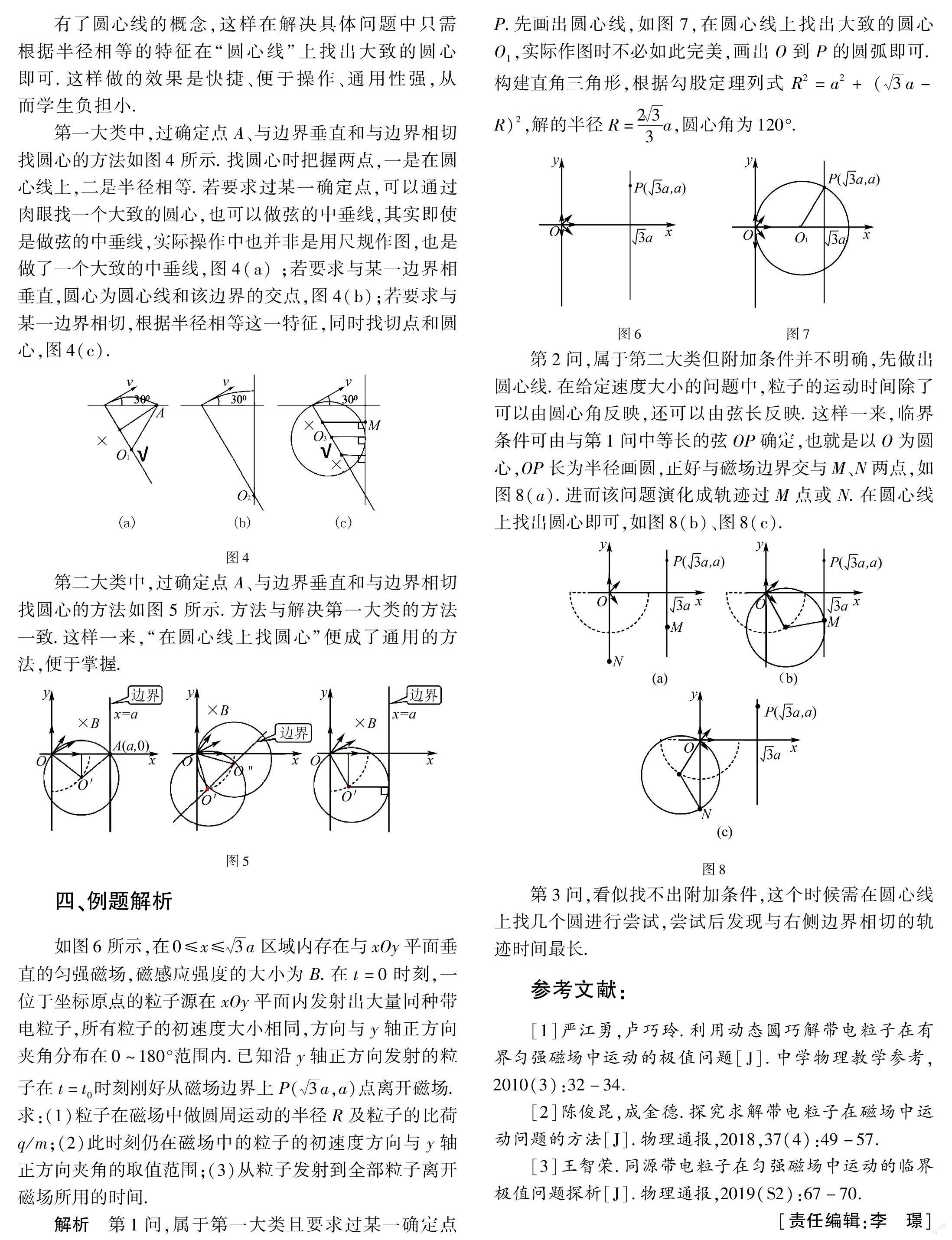
解析 第1问，属于第一大类且要求过某一确定点P.先画出圆心线，如图7，在圆心线上找出大致的圆心O1，实际作图时不必如此完美，画出O到P的圆弧即可.构建直角三角形，根据勾股定理列式 R2=a2 + （3a-R）2，解的半径R=

233a，圆心角为120°.

图6图7

第2问，属于第二大类但附加条件并不明确，先做出圆心线.在给定速度大小的问题中，粒子的运动时间除了可以由圆心角反映，还可以由弦长反映.这样一来，临界条件可由与第1问中等长的弦OP确定，也就是以O为圆心，OP长为半径画圆，正好与磁场边界交与M、N两点，如图8（a）.进而该问题演化成轨迹过M点或N.在圆心线上找出圆心即可，如图8（b）、图8（c）.

图8

第3问，看似找不出附加条件，这个时候需在圆心线上找几个圆进行尝试，尝试后发现与右侧边界相切的轨迹时间最长.

参考文献：

[1]严江勇，卢巧玲.利用动态圆巧解带电粒子在有界匀强磁场中运动的极值问题[J].中学物理教学参考，2010（3）：32-34.

[2]陈俊昆，成金德.探究求解带电粒子在磁场中运动问题的方法[J].物理通报，2018，37（4）：49-57.

[3]王智荣.同源带电粒子在匀强磁场中运动的临界极值问题探析[J].物理通报，2019（S2）：67-70.

[责任编辑：李 璟]