动力总成悬置性能计算程序的改进研究

林文干 方劲松 阳仁松 李浩亮

东风汽车股份有限公司商品研发院 湖北武汉 430057

1 前言

汽车动力总成悬置系统是指动力总成与车架或车身之间的弹性连接元件共同构成的系统。发动机动力总成通过悬置元件安装在汽车车架或车身上。悬置系统既要隔离发动机向车架传递振动，又要隔离路面不平等激励传给发动机的振动。同时，悬置系统还应能有效限制发动机的最大位移，以避免发生与相邻零件的碰撞与干涉，确保发动机正常工作。悬置系统解耦分析和优化目的是寻求悬置元件各向刚度、弹性中心位置和各弹性主轴方向与总体坐标系夹角等参数的最优设计方案，使该悬置系统隔振效果最大化[1]。

动力总成悬置系统性能分析有许多方式进行，如多体动力学软件建模[2]、 有限元建模[3]、GT-Power等一维软件建模分析等，但最常用的还是利用各个汽车生产厂商自行开发的MATLAB程序进行悬置系统模态计算、解耦优化等，可以灵活地根据不同的需求而修改程序。本公司原有的动力总成悬置系统的MATLAB计算程序已经成功使用多年，但使用中还存在一些需要修改源代码等较为繁琐、数据管理不便的问题。为了使用的便利性需要改进程序，即在保证程序计算核心不变的基础上，采取了以下措施来提高易用性和计算速度：

a.采用通用办公软件MS Excel管理输入、输出数据，而无需修改程序的本身代码；

b.输入、输出参数可用常见的单位，避免单位转换错误；

c.计算核心模块外置，防止误操作修改；

d.程序自动识别各自由度的频率和解耦率，可用于结果判定和储存优化计算结果；

e.按悬置软垫的设计公差，用指数增量进行搜索，减少优化计算的循环次数；

f.采用并行计算，充分利用最新计算机多核心计算的优势，提高优化计算的速度；

g.可以按照悬置软垫的压剪比搜索计算，提高计算速度和优化结果产品化的可能性；

h.增加悬置点坐标和安装角的优化计算。

2 悬置系统设计计算理论

动力总成悬置系统解耦分析的计算方法大多是将发动机动力总成处理为由质心、质量、惯性矩、惯性积描述的六自由度刚体，将悬置元件处理为悬置点的无阻尼弹簧，将车架处理为刚性基础，建立悬置系统基于矩阵形式的无阻尼自由振动方程[4]。常规的被动隔振系统的主要参数定义如图1所示，主要参数是被支撑物体的质量和转动惯量、每个隔振垫的平动和转动刚度以及其相对于质心坐标系的坐标和定位方向。

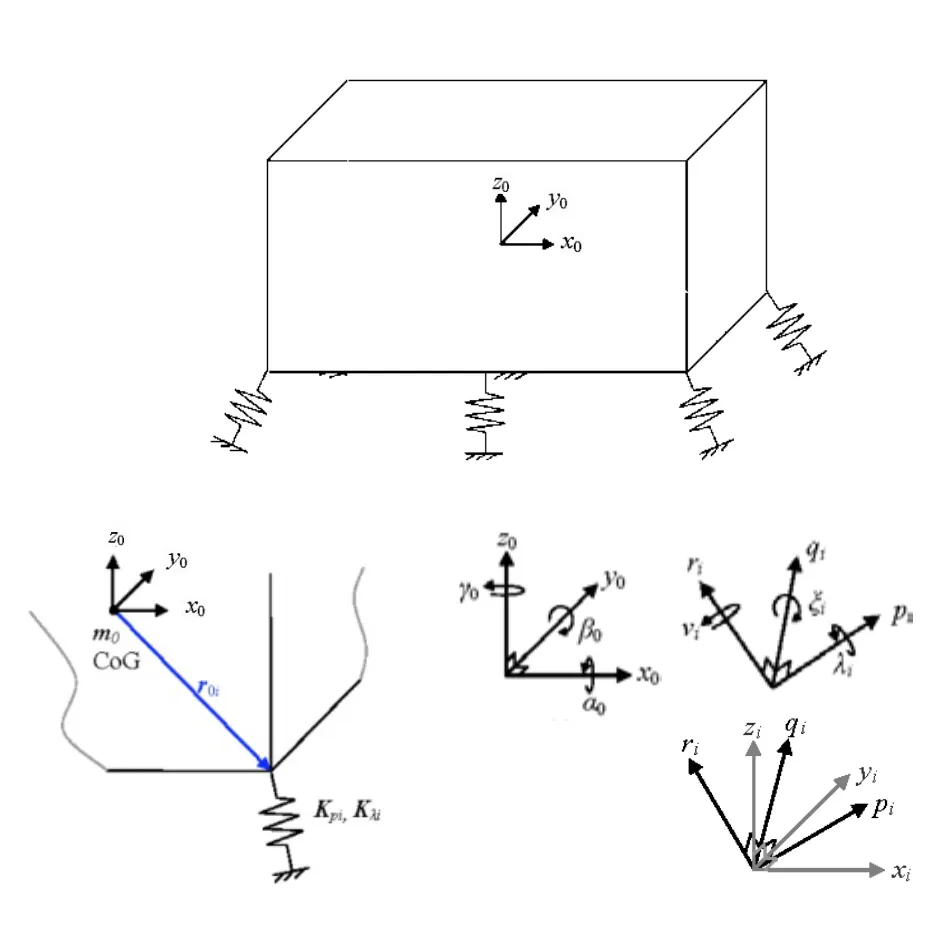
图1 常规被动隔振系统的主要参数定义

系统的运动方程为：

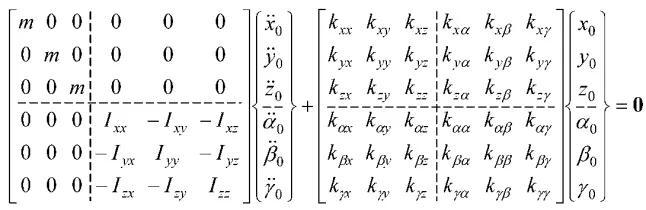
其分块矩阵形式如下：

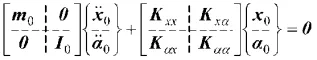
式中，

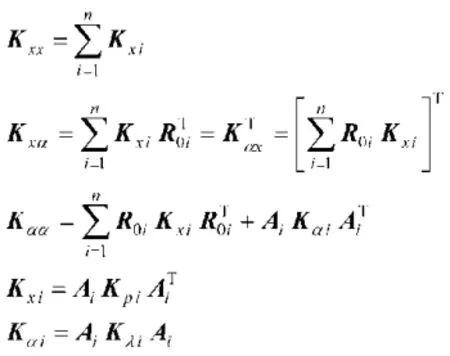
n为隔振垫的数量。

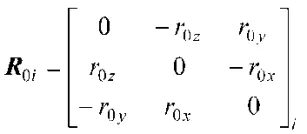
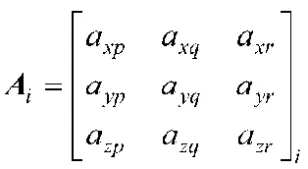
3 改进输入参数管理

为了便于管理输入参数，采用通用办公软件Microsoft Excel的表格文件作为程序输入文件，而且数据格式也与设计汇报的PPT一致，可以直接与PPT文件互相拷贝数据。悬置系统设计计算的输入数据如图2所示，优化计算的输入数据如图3所示。由于MATLAB程序是按位置读取数据，因此使用时不要改变文件中输入数据部分的格式（如增减单元格等），只能修改数据。

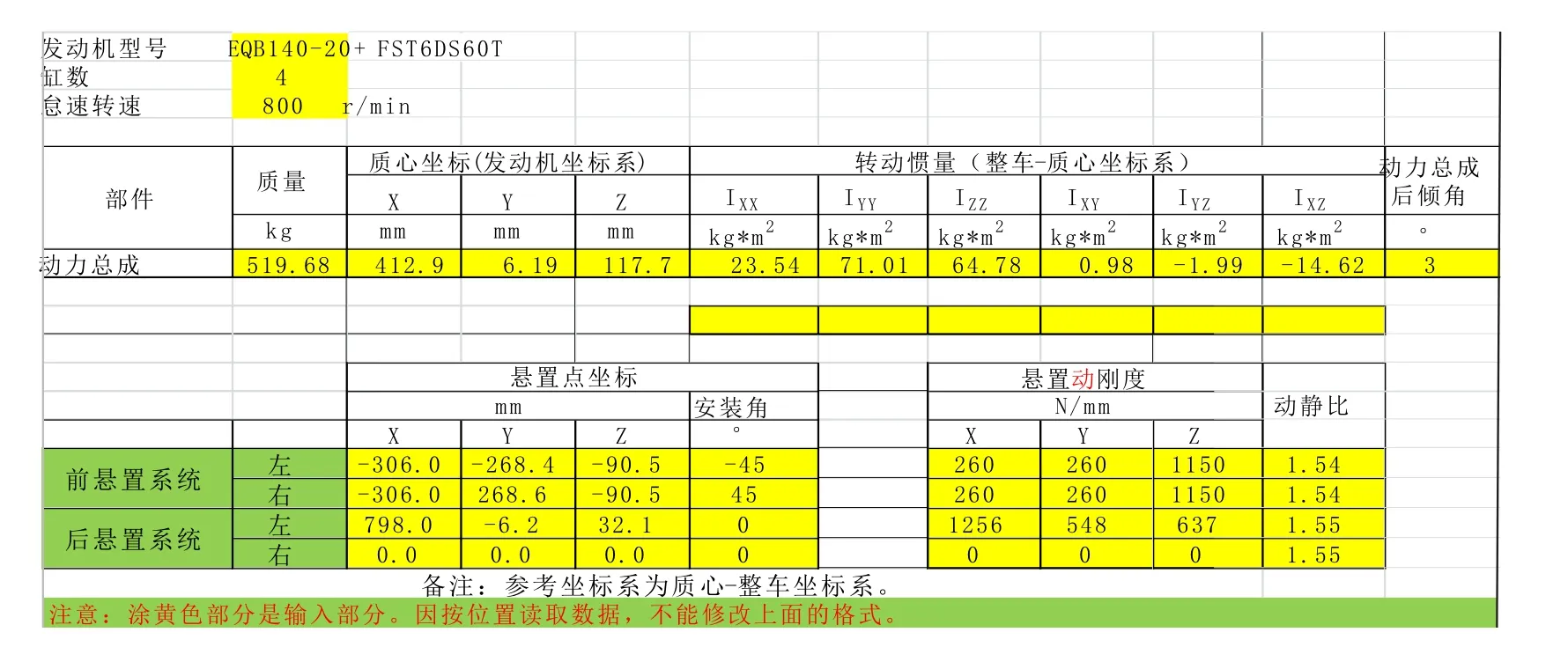
图2 悬置系统设计计算的输入数据表格

图3 悬置系统优化计算的输入数据表格

动力总成的质量属性包括动力总成的质量、质心在发动机坐标系中的坐标（这个坐标值不参与计算），以及在动力总成质心坐标系中的转动惯量。它们主要来自于转动惯量试验台的测试结果。通常动力总成在整车上的布置会后倾3°～5°，这个微小的倾角对模态频率的影响较小，但会影响解耦率结果，因此应根据倾角转换转动惯量试验台测得的转动惯量值。

悬置点坐标是各悬置软垫的中心在动力总成质心坐标系下的坐标值。常见的前悬置V型布置，前左悬置的安装角度为负值，前右悬置的安装角度为正值。

悬置软垫动刚度是在悬置软垫自身坐标系下的动刚度，按照整车结构布置需对应到整车坐标系的X、Y、Z方向，且是安装角度为0的数据，计算程序中会根据输入的安装角度自动转换。动静比数据主要是为了估算动力总成装配时悬置软垫的静位移，防止静位移过大而降低隔振效果和软垫寿命。

4 计算程序的改进

动力总成悬置模态频率和解耦率计算程序以及解耦优化程序的两个MATLAB程序是需要改进的程序。因为之前所有的输入数据都需要在源程序中手工输入，费时且容易出错，其计算结果输出是在MATLAB的信息输出窗口显示，不便于数据管理。通过将输入输出改为Excel文件、将计算核心独立出来以后，对于大多数常规计算，只需要修改Excel输入文件中的数据，即可直接运行MATLAB解耦计算程序或解耦优化程序得到计算结果的Excel文件。

4.1 计算结果中分离各自由度的频率和解耦率

动力总成悬置系统解耦率的MATLAB计算结果，是按系统模态频率从低到高排列的6×6矩阵，而对结果分析则需要按在模态能量中占主导的自由度方向进行结果判断[5]。解耦率矩阵的1～6行分别对应X、Y、Z三个方向的平动（定义为Tx、Ty、Tz）和绕X、Y、Z轴的三个转动（定义为Rx、Ry、Rz），每行中最高值的列数对应的模态频率即为该自由度的模态频率。程序分离出模态频率和解耦率后就可用于结果判断和计算结果存储。

采取模拟人工检视结果的方法，由程序自动识别各自由度的频率和解耦率，即用指令“[Dcp,Ind]=max(Dc_s);”找出解耦率矩阵各列中的最大值Dcp及其所在行数索引Ind。给各自由度的解耦率和频率变量赋值0（如：TX=0; f_TX=0; 其中TX表示Tx自由度的解耦率，f_TX表示Tx自由度的频率，以此类推），防止因耦合严重造成该变量未赋值而为空，导致程序报错而退出循环。然后逐个比较行索引Ind的值而将解耦率和频率赋给对应的变量：

最后，“Rst=[frq;Dc_s]”将频率和解耦率矩阵合并为一个矩阵，用指令“csvwrite('Rst.csv',Rst);”将计算结果输出到名为Rst.csv的文本文件中，可用Excel打开，数据的第一行为系统模态频率，第二到第七行分别为X、Y、Z、Rx、Ry、Rz这6个自由度在各个模态频率下的模态能量占比，也即该自由度下的解耦率。

4.2 悬置系统优化计算方法

因悬置系统优化计算不是一个单值收敛的问题，在不同的悬置软垫刚度组合、不同的结构布置下均有特定的最优值。用常规的MATLAB优化函数，或是文献上经常使用的响应面优化算法或遗传法优化算法[6]，得到的结果方案较少，而且通常也难以在生产中实现要求的刚度组合。为全面评估各参数的影响，用遍历法把所有可能的参数组合计算解耦率，将符合设计要求的参数组合记录下来，然后从中选择合适的值进行产品试制。

用于优化的参数定义如图3所示，主要参数是悬置软垫的三向动刚度、坐标和绕X轴偏转角度的优化计算范围。本公司的主要产品是轻型载货汽车，动力总成都是纵置，前后悬置的左右两边均用相同的刚度值，左右悬置对称布置，以减少优化循环计算的次数。

4.3 指数增量的优化计算

因为参数组合计算是一个级数级的计算，每个参数的分级越多，则计算时间成倍数上升。原优化计算程序是采用等增量计算，如从100 N/mm到2 000 N/mm的范围内以10 N/mm的增量计算，则需要计算190次。考虑到悬置软垫的动刚度制造偏差要求通常为15%，则等增量计算对于大刚度范围内显然过于密集，小刚度范围内则相反。若采用指数增量，则可大幅度降低计算次数，此时，每个动刚度的计算方法为：

式中，x为计算范围的最小值；p为增量百分比。

则计算次数：

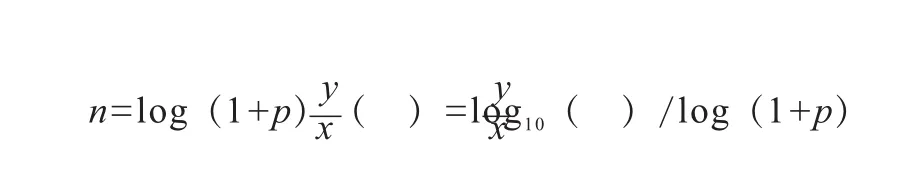
以增量p=10%为例，100 N/mm的增量为10 N/mm，2 000 N/mm的增量为200 N/mm，则计算次数仅为33次，相比等增量计算时的计算时间会下降5.7倍。对应的MATLAB指令为：

为了避免在循环中逐一计算循环变量，影响计算速度，因此预先计算循环变量数组，在循环中按循环索引直接调用，对应的MATLAB指令为：

4.4 解耦优化的并行计算

现在的计算机都是用多核CPU的方式提高计算速度，特别是一些计算服务器的CPU核心多达数十个，理论上会比单核计算的速度提高数十倍。MATLAB的计算默认是单核计算，将程序中的for循环语句用指令parfor替代，MATLAB会自动启动并行计算（需要安装Parallel Computing Toolbox，默认启动的计算核心数量需要预先设置（如图4）。

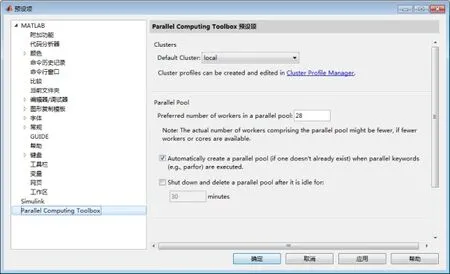
图4 MATLAB并行计算的预设项

但是改为多核计算会有许多限制，如parfor指令仅能用于最外层循环，等等。且当最外层循环数较少时，如只循环数为5时，则只有5个CPU内核参与计算，其它内存处于闲置状态，因此用于parfor指令的变量循环数目应尽量多。将前后悬置的主要刚度组合起来作为最外层循环，以达到最大可能地让计算机满负荷运行，计算程序如下：

4.5 按照悬置软垫的压剪比搜索计算

动力总成悬置系统一般是利用橡胶悬置软垫的剪切刚度较低的特性进行隔振，最好是在主振动方向上橡胶悬置软垫的振动变形是纯剪切状态。橡胶悬置软垫的压缩刚度和剪切刚度的比值（简称：压剪比）的范围较小，一般在4～8之间。用剪切刚度范围作为优化计算的循环变量，而压缩刚度范围利用压剪比来计算，例如：当前悬置的压缩刚度在100 N/mm到2 000 N/mm的范围内搜索计算，以10%的增量需要计算33次，而按压剪比范围以10%的增量则只需要计算8次（4、4.4、4.8、5.3、5.9、6.5、7.2、8），这样计算时间还会缩短 ，更可以提高优化计算结果，实现产品化的可能性。

4.6 悬置系统优化计算结果的判断

原程序在当有计算结果满足判据时，会在信息输出窗口中显示结果。当满足条件的计算方案较多时，则从中找出合适的结果较为繁琐，而且结果显示会大大降低程序的运算速度。因此，采用先将优化计算结果存入数组中，计算结束后再保存在Excel文件中，用Excel管理和分析优化结果，即使有数千组结果，也能方便地比较不同结果间的差异，也更容易从中找到易于实现产品化的优化结果。

由于采用并行计算，就不能用数组下标（如：Opt_Rst(i)=[Rst]）的方式存储结果，所以用在结果数组后面增加一行的方式保存结果，即：Opt_Rst=[Opt_Rst;Rst]。

针对轻卡的动力总成悬置系统设计计算，已经总结了较为完备的解耦评价方法，这些评价方法在MATLAB中都是可以实现的，对应的MATLAB语句如表1所示。

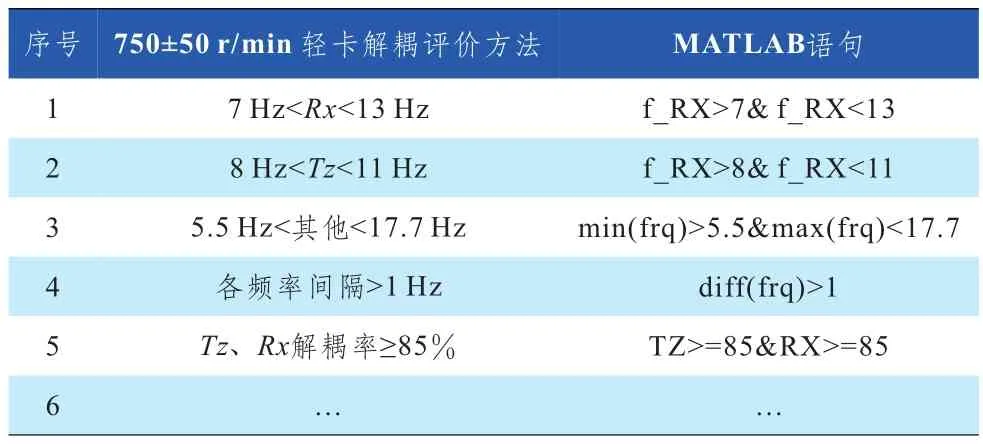
表1 750±50 r/min轻卡解耦评价方法和对应的MATLAB语句

在常规的设计中，要满足表1中所有的设计要求是非常少见的，通常是先从最关键的特性开始，逐步增加优化条件，从而得到最优的计算结果。关键的特性包括Rx的频率和解耦率、Tz的频率和解耦率，如果在合理的悬置刚度范围内都不能满足，那么就需要重新布置悬置系统结构。

5 解耦计算程序的使用

修改之后，动力总成悬置系统解耦计算的主要工作量由修改MATLAB源程序变为在Excel中编辑输入参数，降低了工作的复杂度。对于一个新的动力总成悬置系统设计计算，修改输入参数：打开输入Excel文件，在修改底色为黄色部分的数值（如图2），包括动力总成的质量、转动惯量、悬置点坐标、悬置动刚度。输入完成后，在下方会简单计算一下静载荷、静位移等。在文件浏览窗口中双击打开解耦计算的MATLAB程序，先检查输入文件名是否正确，然后点击“运行”按钮完成运算。计算生成csv文本文件，可用Excel打开编辑，如图5。

图5.解耦计算结果用

6 解耦优化程序的使用

与常规解耦计算的步骤相同，在输入Excel文件中还要定义参数优化计算的范围。其中，刚度最小值和最大值设为相同，以及坐标和安装角的增量设为0，则该参数将不参与优化计算。优化计算结果文件打开后的格式如图6所示，其中结果数据的排列次序和数量可以自定义。

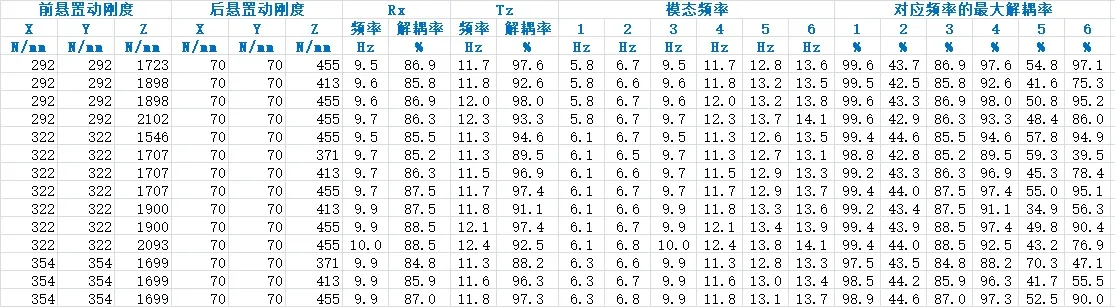
图6 解耦优化结果示例

7 结论

经过一系列改进，动力总成悬置性能计算程序大幅度地提升了程序的易用性和计算速度，从而提高了工作效率和质量，在产品开发和解决产品车NVH性能上取得了较好的效果。改进后的程序在本公司和相关公司得以应用，并在1年内完成了20余辆车型的怠速NVH性能改善工作，取得了良好的经济效益。