基于滑动窗的Needleman-Wunsch 算法硬件加速方案设计与实现

肖俊杰

（上海交通大学电子信息与电气工程学院，上海200240）

0 引言

生物序列比对是生物信息学和计算生物学的基本问题之一，它旨在找出一个未知序列与已知序列在结构和功能上是否相关，这对于疾病的早期防治和药物工程至关重要[1]。Needleman-Wunsch 算法[2]是一种广泛使用的序列比对算法，用于全局比对两个序列之间的相似性。这一算法基于动态规划实现，可以求得比对的最优解，但其时间复杂度与序列长度的乘积成正比，考虑到生物序列数据库的巨大规模和其指数增长率，需要更快的计算技术来应对这一问题。

高算力的并行结构为解决这一问题提供了机会，但是Needleman-Wunsch 算法内部数据之间存在依赖性，需要各计算节点之间相互通信。现有计算方法大多基于波前进位（wave-front）[3]这一并行方式进行优化删减[4-6]，但其访存特征不规则，难以实现高效的访存调度，有限的存储资源和过多的片外存储器访问导致并行效率下降成为了硬件优化的主要阻碍。因此本文提出了一种基于滑动窗的解决方案，采用了通用化的并行策略，简化了对Needleman-Wunsch 算法进行并行的难度；并提出一种延时串连的脉动阵列（systolic array）[7]结构，减少了对存储的访问。为与不同加速方案下的计算和存储特征相匹配，本文基于粗粒度可重构阵列（CGRA）[8]对改进前后的方案进行了比较，并与通用计算架构下的解决方案对比，量化本文方案在执行时间和执行效率方面的优势。

1 Needleman-Wunsch算法

Needleman- Wunsch 算法的目标是在序列X=x1x2…xi…xM（序列长度为M）和序列Y=y1y2…yj…yN（序列长度为N）之间寻找最佳的全局匹配结果。该算法建立了一个(M+1) ×(N+1) 的分数矩阵F，其中矩阵的元素F(i,j)表示X的子序列x1x2…xi和Y的子序列y1y2…yj比对的得分，分值越高表示两条序列的相似性越大。矩阵的最后一个元素F(M,N)为序列X和序列Y的最优比对得分，最优比对结果通过回溯得出。该算法分为初始化、填充和回溯三个步骤，如图1 给出的两条示例序列所示。

分数矩阵的第一行和第一列被初始化，其余元素的值由其左元素、上元素和对角线元素的值确定，其填充规则如下：

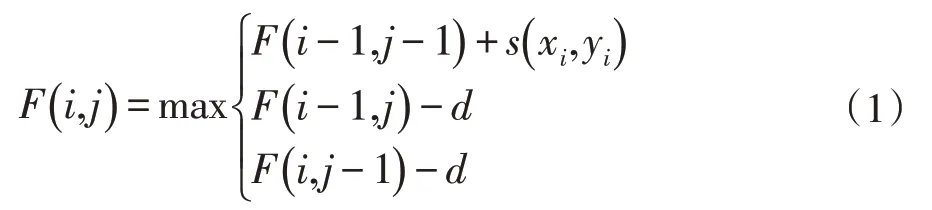
上述式子表明了位置(xi,yi)的3 种更新方式：通过（xi-1,yj）的垂直方向，此时序列X需要插入空位，罚分为-d；通过（xi,yj-1）的水平方向，此时序列Y需要插入空位，罚分为-d；通过（xi-1,yi-1）的对角方向，此时序列匹配成功，得分为s（xi,yi）。

图1 Needleman-Wunsch算法执行步骤

回溯过程从F(M,N)开始，如图1 所示，以箭头标记的方向追溯路径来源，通过箭头的方向确定是否需要在序列中插入空位，获得具有最优解特性的匹配结果。

Needleman-Wunsch 的填充阶段本质上是二维动态规划数组的建立阶段，其时间和空间复杂度均为O(M×N)，是整个算法计算、访存最密集的部分。又由于动态规划的特点，需要各个节点之间相互通信，这一特性增大了Needleman-Wunsch 算法并行化的难度，使其只能以对角线条带（diagonal strip manner）的形式进行内存访问，这种不规则的访问方式破坏了数据的空间局域性。目前的加速平台通常采用一级或多级高速缓存（cache）来提升访存的性能，但cache 的容量有限，单纯增大并行度并不能显著提升系统的性能，反而可能降低系统的存储带宽和增大缓存缺失率。采用合适的并行计算方法提高计算和访存的效率成为了加速Needleman-Wunsch 算法的关键。

2 加速方案设计

2.1 并行特征提取

依据公式（1），Needleman-Wunsch 算法在执行比对任务时内部的数据存在依赖关系，即元素F(i,j)的计算依赖于相邻三个元素：F(i,j-1)、F(i-1,j)和F(i-1,j-1)，只有这三个元素计算完成后才开始计算F(i,j)。因此通常的串行方式是按照矩阵的行或者列逐层进行运算，如图2（a）所示。这种方法在一个时间步内只能处理矩阵的一个元素，计算效率低，而且下一个节点的计算操作数来自前一节点的计算结果，不能简单地对矩阵不同位置的元素进行并行展开。

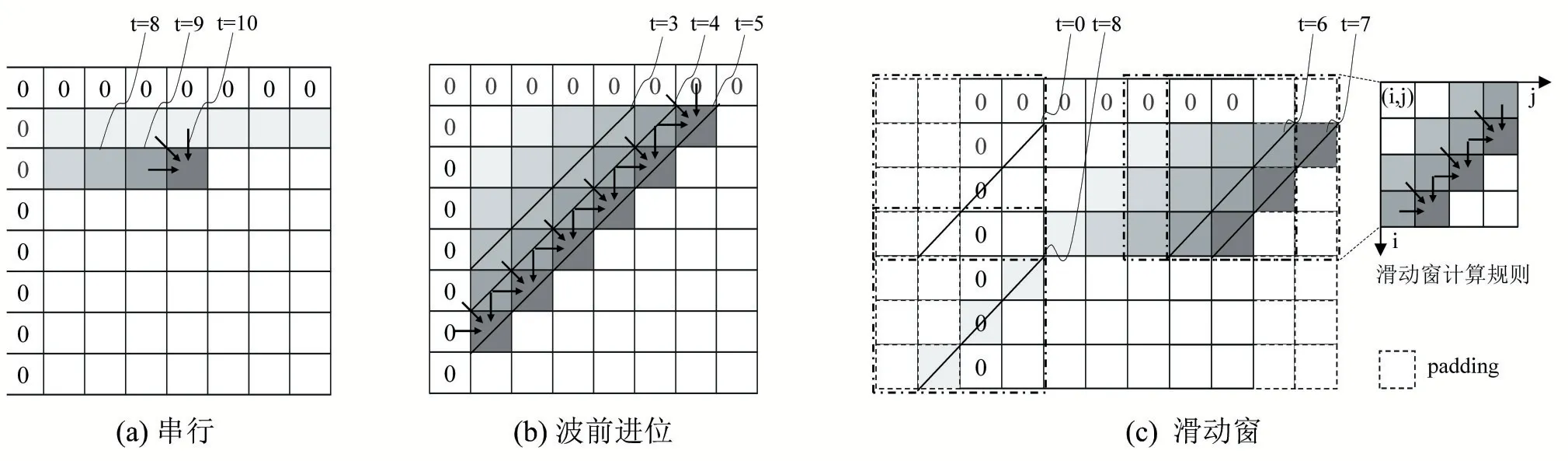
图2 分数矩阵填充步骤的实现和优化

但不难发现当矩阵某一元素F(i,j)的计算完成后，其右方的元素F(i,j+1)和下方的元素F(i+1,j)就可以开始计算，即位于矩阵同一条反对角线上的元素不存在数据相关，从矩阵左上角的第一个元素开始沿着对角线方向通过波前进位的方式进行并行处理，就能够在一个时间步内同时处理同一条反对角线的元素，如图2（b）所示。针对波前进位的优化主要是通过不同的分块策略实现计算和访存之间的平衡，如图3 所示，但对角线元素数量不一使得计算和访存依旧是不规则的，并行效率不高。

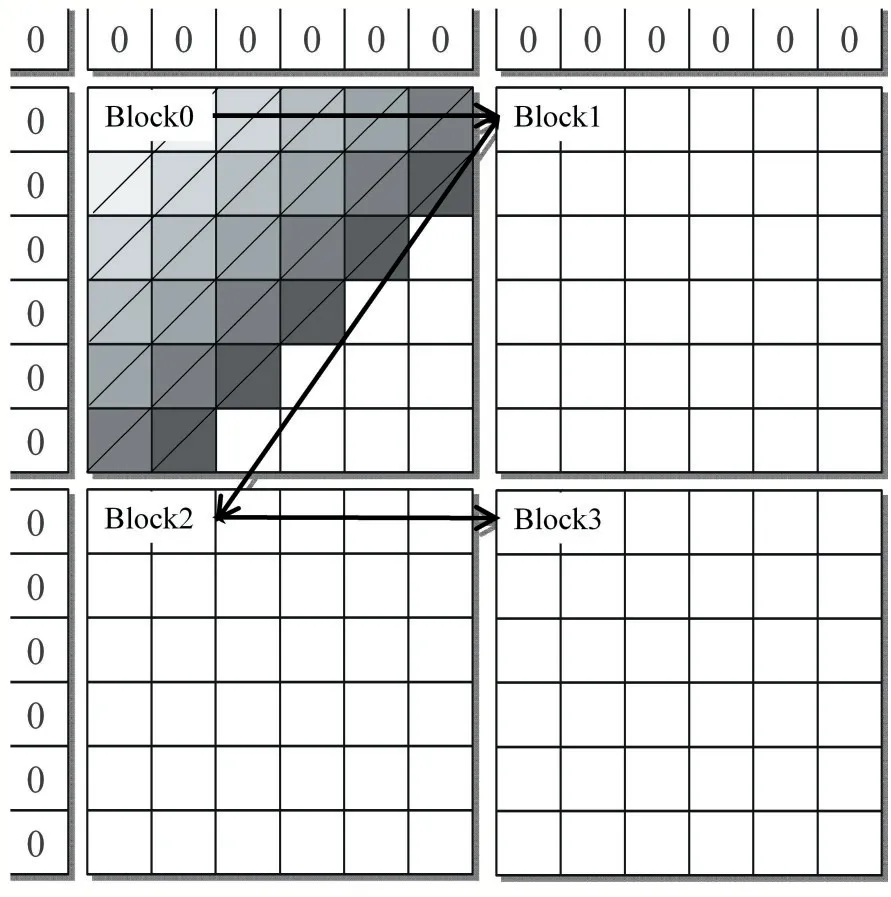
图3 分数矩阵的分块

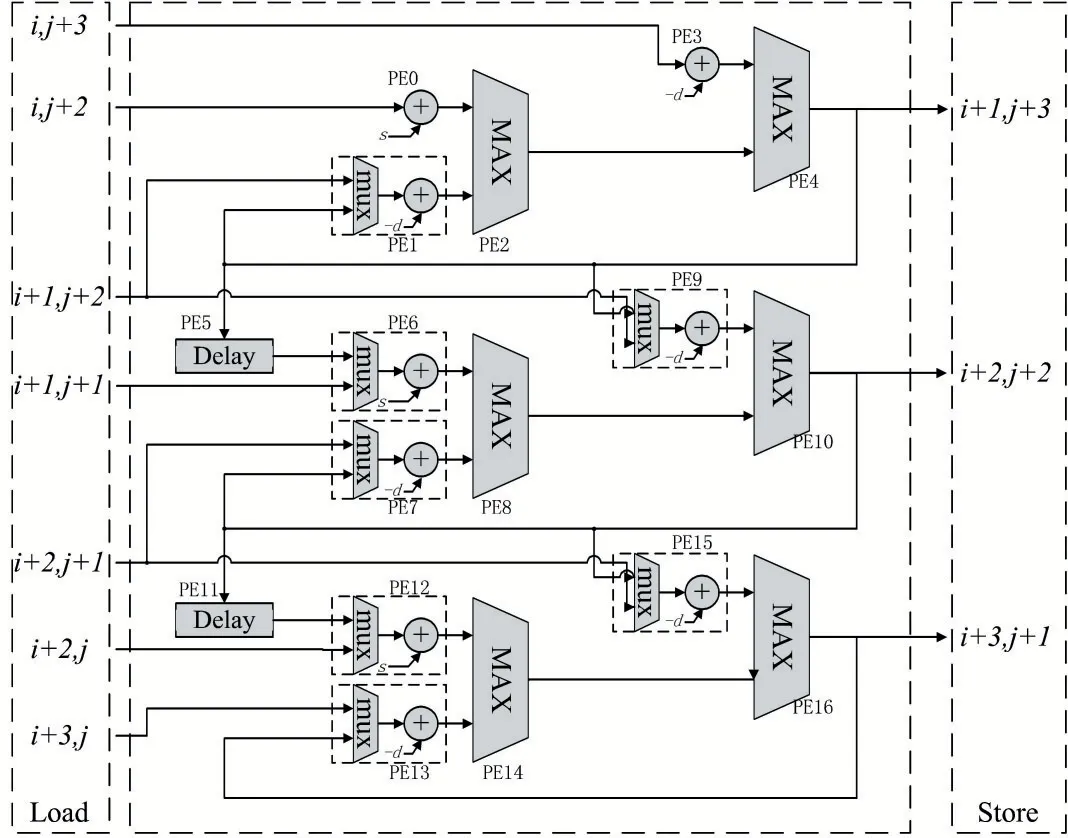
图4 滑动窗数据流图

2.2 并行策略改进

本文利用串联延时脉动阵列结构对上述策略进行了改进，提出了一种滑动窗式的并行加速方法，不仅考虑了单个应用的特性，还提取出算法的公共特征，得到的计算结构更易于扩展。如图2（c）所示，硬件在每一个时间步内只需要处理单个滑动窗内的元素，每个滑动窗遵循相同的计算规则，并且以边界填充（padding）的形式避免边界条件的判断并保证计算规则的统一。计算规则确保了每个滑动窗内部计算的并行性，滑动窗的大小可以依据片上存储器的容量和计算单元的数量确定。这一方法的好处是滑动窗的计算规则保证了单个滑动窗内的数据不存在相关性，硬件只需要对单个滑动窗的计算进行并行加速。并且边界填充可以在算法的初始化阶段完成，简化了边界条件的判断，提高了资源的利用效率。

以图2（c）为例，假定滑动窗大小为4×4，滑动窗在单个时间步内可同时计算3 个元素的值，在分数矩阵的边界处（图中的t=0 和t=7）额外填充了2 列元素，使得滑动窗可以使用相同的规则进行计算。滑动窗首先进行横向滑动，在计算得到当前位置的结果之后向右滑，并将之前的结果作为新位置下的输入，按照此方式处理分数矩阵的0 至3 行后向下滑，以相同的规律处理矩阵的3 至7 行。滑动窗的滑动过程很容易通过脉动阵列结构实现，脉动阵列结构可以在消耗较小的内存带宽的情况下实现较高的运算吞吐率。而且这种计算方式容易扩展，能够用于不同规模的输入。

这一方法得到的数据流图如图4 所示，在硬件概念上使用计算处理单元（Processing Element，PE）对滑动窗内的元素实现并行计算。因为某一次计算得到的结果会在接下来两次计算中使用，所以计算得分的PE会将结果直接或经过延时后转发给另一个PE，实现局部的数据复用，PE 阵列只有在分数矩阵的上边界和左边界处才需要从存储器中读取操作数，其余时间可以从计算得分结果的PE 处获取。单纯采用对角线展开的方式处理3 个元素需要进行7 次读操作，相比之下采用滑动窗实现只需要2 次读操作，极大地减少了带宽需求。同时，在计算得到矩阵元素分值的同时也可以知道该矩阵元素是由哪个方向的元素得到的，因此回溯方向的保存可以和分值的计算同时进行。此外由于滑动窗是按照矩阵的行、列方向滑动的，在降低了访存次数的同时也降低了对角线条带式访问带来的缓存缺失问题。

3 实验结果与分析

3.1 实验平台

本实验中，我们采用了粗粒度可重构阵列（CGRA）结构来实现滑动窗的结构。粗粒度可重构阵列兼具灵活度和高性能，能够与不同的访存和计算结构相适配，从而对不同的算法提供广泛而灵活的支持。本文基于C++搭建了一个包含典型CGRA 结构的系统级模拟器，用以模拟可重构阵列的执行过程，模拟器包含周期精确的阵列模型和的内存模型[9]，该CGRA 系统结构如图5 所示。

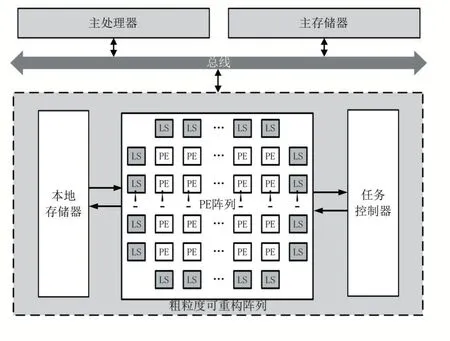
图5 粗粒度可重构阵列系统结构

其中，粗粒度可重构阵列负责处理核心计算，主处理器对系统进行控制，对目标应用进行编译生成带有配置信息的数据流图（Data Flow Graph，DFG），任务控制器对数据流图进行解析，随后向PE 组成的PE 阵列发送配置信息，PE 阵列依据配置完成任务的执行。本地存储器和主存储器构成存储器层次结构，实现高效的数据存储和访问功能，本地存储器采用16KB 的一级cache。

PE 阵列包含有8×8 规模的64 个PE，每个PE 可依据配置字配置成不同的功能，32 个存储处理单元（Load Store Element，LS）分布在PE 的外围负责管理访存请求。每个PE 可以与同行同列的PE 或LS 互连，这种互连方式支持同行和同列的PE 之间相互转发数据，从而实现脉动阵列，大量PE 组成的阵列带来了高并行性，并且PE 计算的结果不需要存回存储器，可以直接转发给下一PE 进行处理，提高了计算效率。

3.2 实验结果分析

为了验证改进后的方案在CGRA 上实现的效率，本文对上一节的三种填充实现策略进行了映射，分别是串行、波前进位和滑动窗式，碱基序列长度均为256，最终得到的实验结果的如表1 所示。表中的PE 数量表示执行应用所需要的PE 总数，表明硬件的资源消耗情况；PE 利用率表示PE 执行有效计算的时间占执行时间的比率，表明硬件的执行效率。

其中方案1 不进行并行、分块等任何优化，作为对比的基准，方案1 中的许多PE 被用于循环控制和边界判断，因此利用率不高。方案2 将矩阵分成8×8 大小的块，采用对角线条带的并行方式，单个块最多可同时计算8 个对角线元素，增大了计算的并行度。但是大并行度也导致了更高的缓存缺失率（cache miss rate），多个请求相互争抢cache 也导致了访存冲突（cache conflict），不规则的对角线计算也使得部分PE 闲置，PE利用率反而有所降低，方案2 相比方案1 最终获得了3.5 倍的加速比。方案3 选择的滑动窗大小为9×9，最多可同时计算8 个对角线元素；由于计算更规则，在相同并行度下减少了用于边界判断的PE 数量；方案3 相比方案1 的加速比提升到了7.5 倍，而且由于方案3 采用脉动阵列实现，降低了访存次数，很大程度上减少了由于缓存访存缺失和访存冲突引起的流水线停顿，相比方案2 获得了2.3 倍的性能提升。

表1 不同映射方式执行时间对比

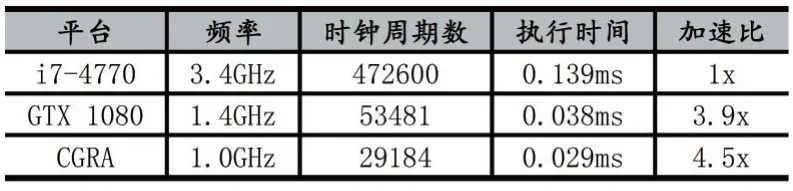
表2 不同架构执行时间对比

表2 给出了本文方案与CPU 和GPU 对比的结果，以验证本文的上述方案相对通用加速平台的性能提升。其中CPU 测试平台采用Intel Core i7-4770 处理器，16GB DDR3 内存，以执行时间作为性能标准，本文提出的方案获得了4.5 倍的加速比。GPU 平台采用NVIDIA GeForce GTX 1080，并使用Rodinia[10]中的加速方案。由于Needleman-Wunsch 算法需要计算节点之间相互通信，GPU 不同线程之间需要频繁同步，因此整体的并行效率不高，本文方案在使用更少计算资源情况下依然获得了15.3%的性能提升，执行效率更高。

4 结语

本文提出了一种基于滑动窗的解决方案来加速Needleman-Wunsch 算法，并基于CGRA 对该方案进行了验证。相比传统波前进位的并行方式，该方案提取了算法的公共计算特征，简化了算法在硬件上的实现难度，使得更多的硬件资源可以用于核心计算；采用串连延时脉动阵列结构降低了访存次数，减少了由于访存延时带来的流水线停顿，与改进前相比获得了的2.3倍加速比，相对CPU 获得了4.5 倍的加速比，相对GPU，在使用计算资源更少的情况下仍然获得了15.3%的性能提升。值得一提的是，本文提出的方案核心是对二维动态规划矩阵的建立过程进行硬件优化，这种优化方法易于拓展到其他具有二维动态规划特性的算法上。