函数极限求解方法研究
2021-05-28谭畅
谭畅
(吉林水利电力职业学院,吉林长春 130117)
极限是《高等数学》中的重要概念之一。极限思想是近代数学的重要思想,是《高等数学》的灵魂,贯彻《高等数学》始终。很多概念都是由极限来定义的,比如导数,定积分,反常积分等等。因此,理解极限思想和掌握求极限的方法是学习这门课程的基本要求。但函数极限问题类型比较多,求解方法也灵活多变,学生往往对极限这一问题感到束手无策。另外,我国现在开设《高等数学》课程的高校使用的教材普遍理论性比较强,并不适合学生自学,像极限这样灵活多变的问题也没有系统的归纳总结过,若教师上课是照本宣科式的教学模式,那学生对极限这样的问题更是一头雾水,当然思路混乱了。因此,鉴于这种现状,笔者结合多年的教学经验和实践总结了求函数极限问题的一般思路,并且对函数极限问题进行了分类,给出了不同类型函数极限的求解方法。
对于一元函数求极限的题目,我们可以按照以下思路进行:
(1)先化简(主要指利用无穷小等价代换);
(2)利用极限四则运算法则,将自变量趋向的数值代入函数表达式计算,若能直接计算出数值,则该数值即为此函数的极限值;
(3)在过程2 中,若不能直接计算出结果,则一定会出现几种特殊情况,判断类型,找对应的求解方法。
1 化简计算
如果题目可以找到合适的方法进行适当化简,那将会起到事半功倍的效果,可以大大缩短做题时间,减轻计算量,这里主要指的是无穷小等价代换。在基本的无穷小等价代换公式的基础上,我们更应该熟记这样一类无穷小等价代换:
□→0 时:

□里面可以是单变量,也可以是一个表达式,只要□内的整体趋向于0,就可以进行无穷小等价代换。值得注意的是,无穷小等价代换只能用于乘法或者除法中,不能用于加法和减法中。
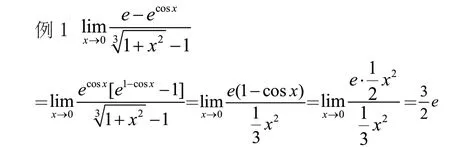
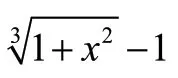
2 利用函数极限四则运算法则带值计算
函数极限四则运算法则:
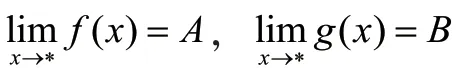
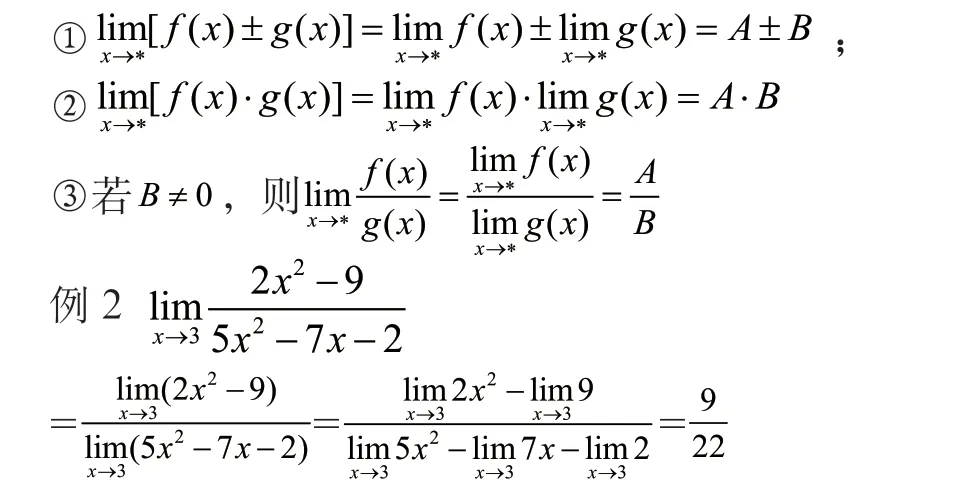
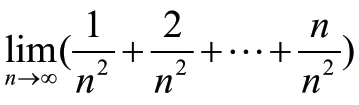
3 判断类型,找对应方法
在上一步中,若利用函数四则运算法则不能直接得出结果,则一定会出现以下7 种特殊类型,我们称之为“未定式”。在以下过程中,若在乘法或者除法中出现极限不为0 的因子,我们要先计算出来。
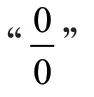
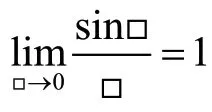

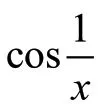
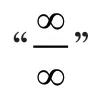
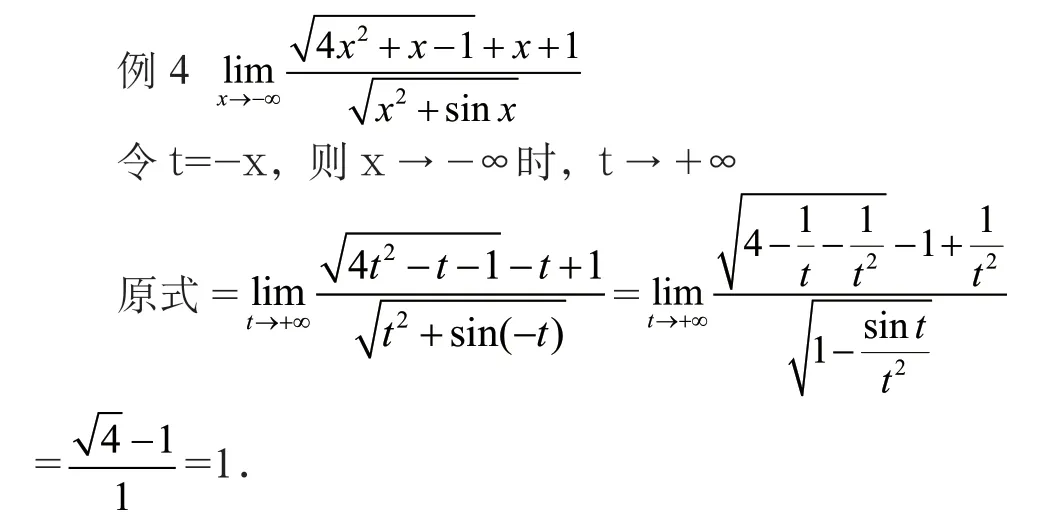
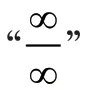
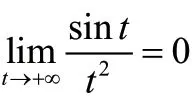
(3)“I”型
方法:①“凑e”(凑重要公式的推广形式:

②“取e”(借助指数函数的性质:e=□)
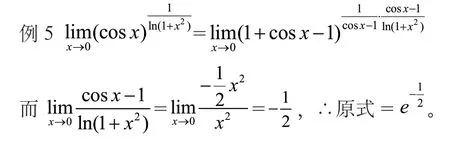
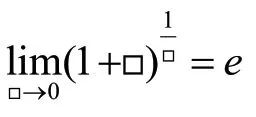
(4)“0”型
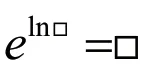
(5)“∞”型
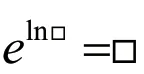
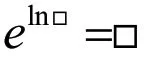
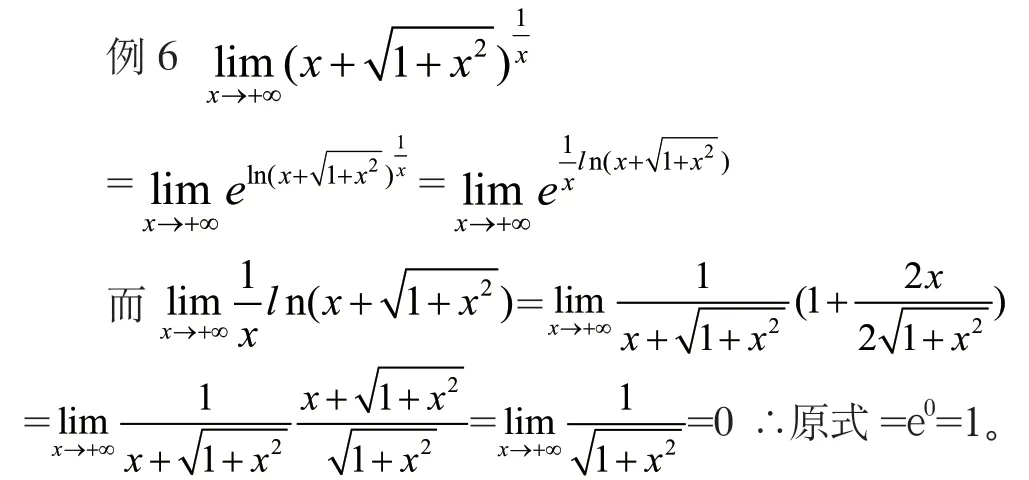
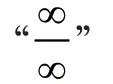
(6)“0·∞”型
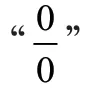
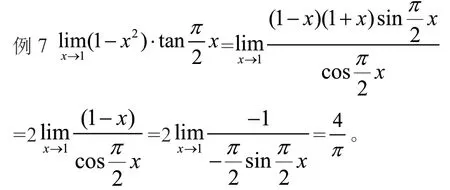
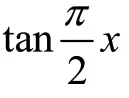
(7)“∞-∞”型
方法:①通分化简; ②倒代换。
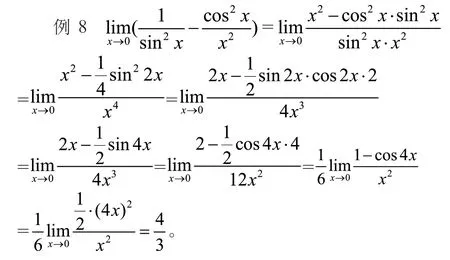
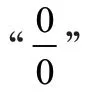
在前面我们介绍过只有有限项和或者差并且每一项的极限都存在时才能使用极限的四则运算法则。若将有限项推广到无限多项和或差的极限问题时,又产生两种常见解题思路。
4 夹逼准则
如果函数f(x),g(x)及h(x)满足下列条件:

在采用夹逼准则求无穷项和的极限问题时要采取合适的方法,对原式进行适当的放缩,使原式恰好夹在极限值相等的两个函数之间。寻找合适的放缩方法需要一定的经验和技巧。若每项的分子或分母都相同时,通常可以寻找两边的最大值和最小值来建立不等式;若每项的分子和分母都呈一定规律变化时,也可以固定分子和分母之中的其中一个,通过放缩另外一项来建立不等式。总之,放缩无定法,还需在实践中不断探索和总结,才能找到便捷之路。
5 定积分思想

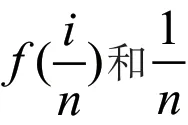
《高等数学》课程中关于极限的类型和求解方法有很多种,本文只对高等院校教学中常见的一些类型及其求解方法进行归纳总结,其他方法不再赘述。希望能带给广大师生一点思考和探索。当然,数学的学习是需要不断思考和总结的,在不断的思考和总结中探索出新的方法和技巧,体会数学的美与乐趣。
