带有双临界指数项的非线性Choquard方程解的存在性

崔雪玲,王非之

(烟台大学数学与信息科学学院, 山东 烟台 264005)

本文研究了下述带有双临界指数项的非线性Choquard问题

(1)

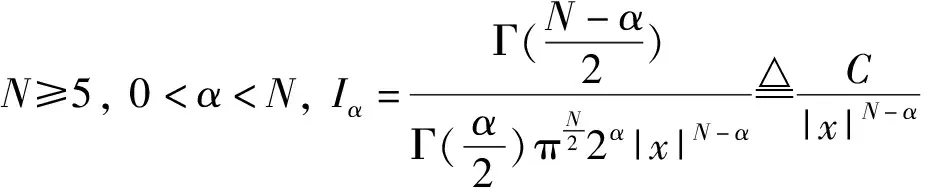
-Δu+u=(Iα*F(u))f(u),x∈N,

其中N≥3,F∈C1(;),f=F′, 证明了若f满足适当的次临界增长条件, 则上述问题存在非平凡解, 而且说明了这些条件是上述问题有非平凡解的必要条件。LI和MA[6]研究了

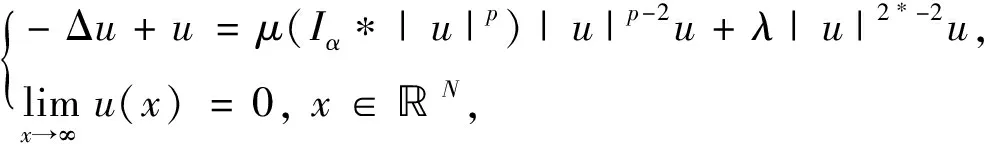
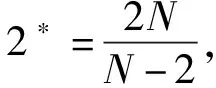
本文在文献[7]的基础上,只在N≥5的条件下得到了问题(1)解的存在性,推广了文献[7]的结论。

以下为本文中要用到的方法。

由Hardy-Littlewood-Sobolev不等式(引理1)和Sobolev嵌入定理, 泛函Jα(u):H1(N)→属于C1(H1(N,)), 定义为

而且

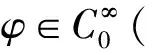
若u是方程(1)的弱解, 则Pohozăev 恒等式P(u)=0[5], 这里P(u):H1(N)→是Pohozăev泛函, 定义为

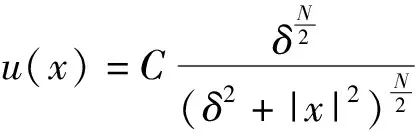
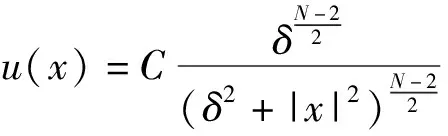
本文结构如下:第1节给出一些预备知识, 第2节建立Pohozăev-Palais-Smale序列, 第3节给出定理1的证明。

1 预备知识

利用山路引理证明解的存在性,考虑山路水平[5]

(2)

这里山路集合定义为

Γ={γ∈C([0,1];H1(N)):γ(0)=0,Jα(γ(1))<0}。

首先给出一些引理,然后计算出式(2)中山路水平b的取值范围。

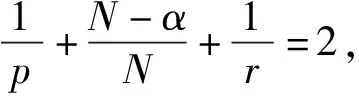
推论1 由引理1,对于任意v∈Ls(N),其中N)且

引理2[9]令Ω⊂N为一个有界区域,q∈(1,∞)且{un}为Lq(Ω)中的有界序列。若un→u在Ω上几乎处处成立,那么在Lq(N)上un⇀u。

下面对山路水平b进行估计。

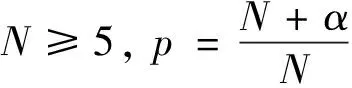
证明令序列 {uj}⊂H1(N){0} 满足和P(uj)=0,那么,

也就表明b≥0。证毕。

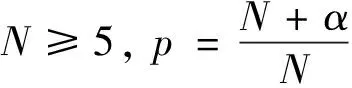
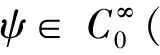
先利用uε(x)来估计b。

由文献[6]和[10],有下述估计,

(3)

(4)

(5)

通过直接计算,对于ε<1,

其中

其中

简单计算得

因此

(6)

类似地,对于ε<1,

其中

其中

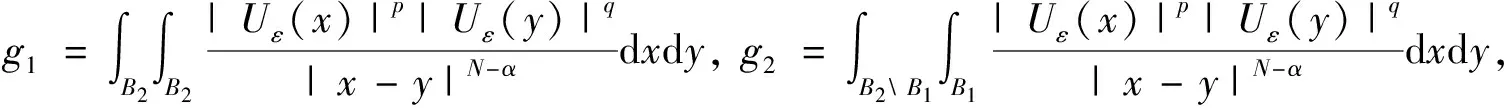
简单计算得

因此

(7)

由于

所以结合式(3)—(7),可得

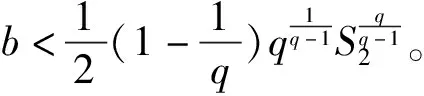
再利用vδ(x)来估计b。

容易看出

(8)

通过直接计算,对于δ<1,

其中

其中

简单计算得

因此

(9)

注意到

其中

简单计算可得

a1≤O(δN),a2=O(δN),

因此

(10)

类似地,对于δ<1,

其中

其中

简单计算可得

因此

(11)

最后

其中

其中

简单计算得

因此

(12)

由于

所以结合式(8)—(12)可得

综上所述, 结论得证。

2 Pohozăev-Palais-Smale序列

本节将构造Pohozăev-Palais-Smale序列。首先给出定义。

定义1 一个序列(uj)j∈属于H1(N)是Jα在水平b的一个Pohozăev-Palais-Smale序列,如果当j→∞时,

Jα(uj)→b>0;

Jα′(uj)→ 0, 在(H1(N))*中强收敛;

P(uj)→ 0。

引理5 对方程(1)对应的泛函Jα及山路水平b, 存在一个Pohozăev-Palais-Smale序列{uj}⊂H1(N), 使得当j→∞时,

Jα(uj)→b>0;

Jα′(uj)→ 0, 在(H1(N))*中强收敛;

P(uj)→ 0。

证明证明分为以下三步进行:

(1)临界水平满足b<∞。

对于任意函数u(x)和τ≥ 0,定义uτ:N→为

直接计算,对于每个τ>0,

(2)临界水平满足b>0。

对于每一个u∈H1(N){0},由Hölder不等式和推论1可得

从而

(13)

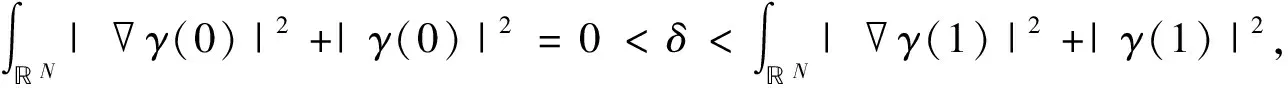
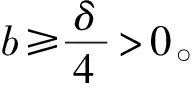
(3)根据文献[11], 对σ∈,ω∈H1(N)以及x∈N, 定义映射Φ:×H1(N)→H1(N), 并且Φ(σ,ω)=ω(e-σx)。对每一个σ∈以及ω∈H1(N), 通过计算, 泛函Jα∘Φ为

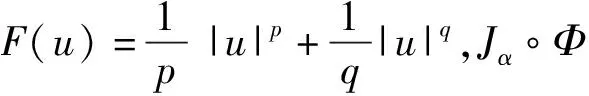
(Jα∘Φ)(σn,ωn)→b,(Jα∘Φ)′(σn,ωn)→ 0,(×H1(N))*。

(14)

因为对每一个(h,k)∈×H1(N), 有

(Jα∘Φ)′(σn,ωn)[h,k]=Jα′(Φ(σn,ωn))[Φ(σn,k)]+P(Φ(σn,ωn))h,

所以P(Φ(σn,ωn))→ 0。我们取un=Φ(σn,ωn)即可。证毕。

3 定理1的证明

本节首先给出一些引理,然后给出定理1的证明。

引理6 假设{uj}是泛函Jα的一个Pohozăev-Palais-Smale序列, 则{uj} 在H1(N)中有界。

证明由于{uj}是H1(N)中的Pohozăev-Palais-Smale序列,

于是,

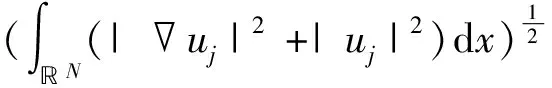
引理7[12]令α∈(0,N)且当j→∞时,uj在H1(N)中弱收敛于某个u0,

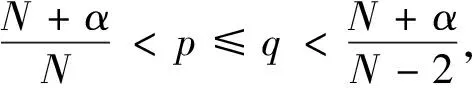
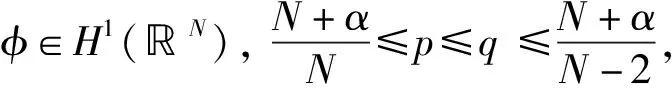
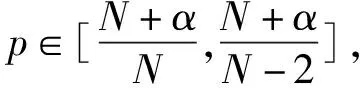
定理1的证明令{uj}⊂H1(N)是泛函Jα的一个Pohozăev-Palais-Smale序列, 那么

并且由引理6, {uj} 在H1(N)中是有界的。于是{uj} 存在一个子序列{un} 在H1(N)中弱收敛于u0, 即un⇀u0。接下来证明u0是问题(1)的解。

由 〈Jα′(u0),u0〉=0得

因此

令vn=un-u0可得,

利用引理7和8, 注意到

由〈Jα′(u0),u0〉=0以及〈Jα′(un),un〉→ 0, 可得

(15)

再一次利用引理7和8, 注意到

由P(u0)=0,P(un)→ 0, 可得

即

(16)

因此, 结合式(15)与式(16), 可得

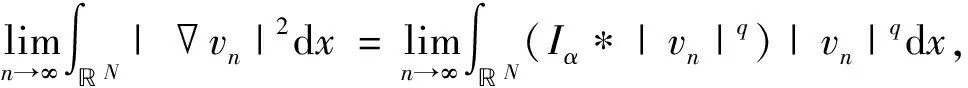
假设

由S1,S2的定义,

于是

(17)

根据上式,下面证明b1=0 并且b2=0。

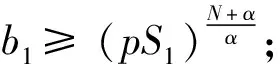
这也与引理4矛盾, 因此b1=0。即证得b1=b2=0。

于是

由上式可知在H1(N)中, 当n→∞时,vn→ 0, 即un→u0,则u0是方程(1)的弱解。证毕。