在界面处引入原子混合层结构的热导性能分析

吕荒芜

（华北电力大学（保定）能源动力与机械工程学院，河北 保定 071003）

0 引言

自20世纪40年代第一代计算机问世至今，大量电子元件的制造技术都达到了纳米级别。纳米材料被广泛应用于电子器件制造行业，例如计算机的芯片CPU、量子级联激光器和场效应晶体管等。高精度带来高运行效率的同时，也会导致更高的热功率，设备运行中产生的大量热量不仅会影响工作效率，还会有降低使用寿命的风险，因此热管理问题的研究刻不容缓。

纳米结构的多样化和易操作性为热管理提供了广阔的发展前景[1-2]。由于纳米结构部件和设备中存在较高的表面积体积比，材料界面处的热传递通常主导着整体的热行为，它们是热载体的散射中心，可以通过调整它的物理特性来控制器载流子的分散强度。因此深入了解界面热导的性能，对研究纳米结构材料的热传输具有重要意义[3]。

1 研究背景

向结构中引入多层复合原子混合层是1种能够有效提高系统界面热导的方法[4]。研究表明，界面的原子在某些特定的排布状态下能够促进界面处的热交换。Tian Zhiting等人将格林函数方法与Laudauer方程相结合，详细阐述了原子混合引起的界面紊乱是如何增加界面处的声子输运和界面热导[5]。Carlos和Rouzbeh[6]利用格林函数法研究了不同固体材料界面上的一系列热导，他们的研究显示，在平滑的界面中引入单层的原子混合层总是能够增强界面的热导，但是根据原子晶体结构的不同，热导的增加也会有所不同，热导增量的变化可以达到1个数量级。尽管学者们已经在构造使界面热导最大化的原子混合层方面取得了许多进展[7-8]，然而目前对混合层的厚度以及温度变化对界面热导的影响的分析仍然缺乏统一和定量的构建模式。

受上述研究启发，该文在2种不同材料的界面处构建原子混合层，采用分子动力学方法对结构进行模拟，讨论了原子混合层的数量以及温度对界面热导的影响。此外，研究人员还详细计算了2种结构的声子态密度和声子参与率，分析了不同结构下系统界面处声子散射的机制。该研究的主要目的是找到合适的原子混合层构建方式，从而改善声子频率失配界面处的热输运。

2 模型构建

如图1所示，研究人员用Atomsk软件构建了理想的Si/Sn界面结构，考虑到计算的精度和系统的运算能力，研究人员将结构的总原子数设置为5120，Si/Sn理想界面处于整个纳米结构的中间位置，界面左侧为Si原子，右侧为Sn原子。研究表明，当分子动力学模拟采用周期性边界条件对导热系数进行计算时，在横截面积为不小于3×3个原胞的情况下，横截面积对导热系数的影响可以忽略。因此，在该研究中，研究人员将横截面面积设置为4 UC×4 UC，x、y、z3个方向上的原胞以4 UC×4 UC×40 UC（Unit Cell）的形式进行排列。研究人员将以Si/Sn理想界面为基础，采用替换原子的方式在理想界面处引入原子混合层纳米结构。

图2是理想Si/Sn界面处引入Si/Sn原子混合层的纳米结构，研究人员在图1的基础上，以界面为中线，在保证模型总长度不变的情况下向界面处引入1～10层的原子混合层，混合层中的Si、Sn原子数目各占50%，并且随机排布。

3 计算方法

所有的非平衡分子动力学模拟都是在LAMMPS软件环境下运作的，由于Stillinger-Weber（SW）势函数已经被证实能够较为精确地解释硅基纳米结构的热力学特性和界面热导，因此该模拟选取了SW势函数描述Si-Si、Ge-Ge、Sn-Sn、Si-Ge、Sn-Ge以及Si-Sn之间的力关系。模拟计算热性质示意图如图3所示，为了防止与外界产生热量交换，研究人员固定了2个外壁，并将该区域内粒子的速度设置为0，然后分别将紧邻边界区域设置为热源和热汇，从而建立温度梯度。为了节约计算资源，研究人员将模拟的时间步长设为0.001 ps。在非平衡分子动力学模拟的第一阶段，使系统处于压力为0、温度为300 K的环境下，采用等温等压系综（NPT）对系统进行弛豫。在系统模型达到完全弛豫后，在X和Y方向上施加了周期性边界条件，并在Z方向上采用了固定边界条件。为了使系统的能量分布处于均匀的状态，研究人员让系统继续在正则系综（NVT）下弛豫2 ns，系统再次达到平衡后，模拟将在微正则系综（NVE）下继续运行10 ns，与此同时，每隔1000个时间步长记录1次原子信息。

图1 理想Si / Sn界面结构

图2 理想Si/Sn界面引入原子混合层结构

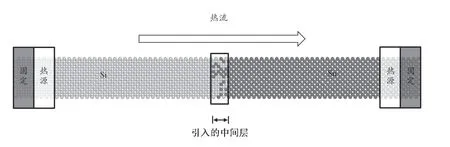
图3 NEMD 模拟计算热性质示意图

界面热阻R可以表述为温度梯度ΔT与热通量Jz的比，如公式（1）所示。

温度梯度ΔT是通过对于温度曲线进行线性拟合获得的，热通量Jz如公式（2）所示[9]。

式中：E为能量；t为模拟时间；A为横截面积；hot bath为热源。

根据傅里叶导热定律，热导率k如公式（3）所示。

考虑横截面积为A、长度为d的1个长方体材料，其热导K与热导率k的关系如公式（4）所示。

实际分析中更常用的是单位面积的热导，通常用符号G表示。求解该长方体材料单位面积的热导如公式（5）所示。

声子态密度（PDOS）是表征系统中声子活动的强大工具。它是根据所有原子的速度自相关函数（VACF）的傅立叶变换计算得出，如公式（6）所示。

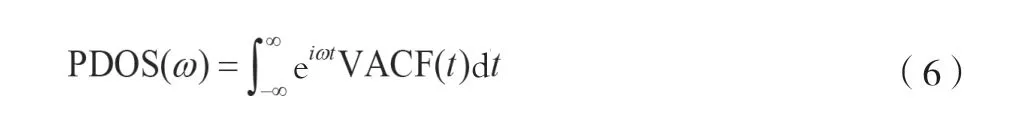
式中：PDOS（ω）为振动频率为ω时的总声子态密度。

VACF（t）可以表示为如公式（7）所示。

式中：vi（t）为粒子i在时间t下的速度矢量；N为系统中的原子数； 为系综平均。

声子参与率（PPR）是了解声子输运的另一种有效方法，它可以用来定量描述声子局域化效应。PPR如公式（8）所示。

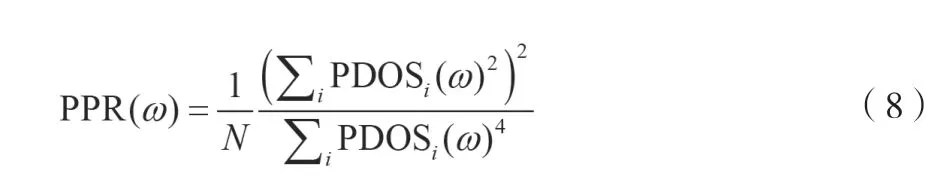
式中：N为系统中总原子数；为频率为的第i个原子的声子态密度。

4 结果与讨论

为了研究薄膜厚度对跨界面热传输的影响，研究人员让原子混合中间层的厚度在0个、2个、4个、6个、8个和10个原子层之间变化。图4为不同原子混合层厚度下系统的界面温度分布图。从图4中可以观测到Si/Sn界面处的温度出现了急剧下降的情况，该情况可以直接归因于界面热阻的影响。值得注意的是，不同厚度的原子混合中间层，其界面处处的温度分布具有不同的形状。随着中间层厚度的增加，界面处温度降的变化趋势较为一致。

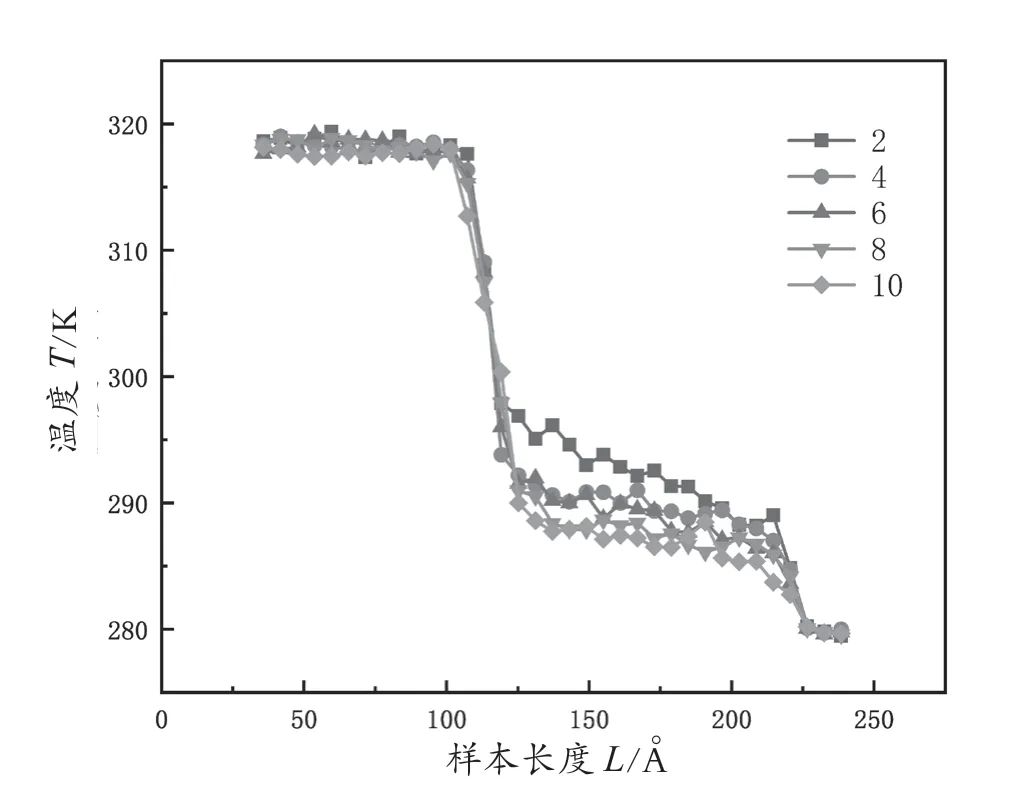
图4 引入原子混合层系统的界面温度分布

为了分析原子混合中间层的厚度对热导率的影响，研究人员计算了不同混合层数下系统的热导。在分子动力学模拟过程中，将温度设置为300 K，样本长度设为23.844 nm（238.44 A°）。模拟结果如图5所示，从图5可以看出，在中间层原子层数从0层变化到2层的过程中，系统的界面热导大约提升了31.6%。而随着原子层数从2层变化到10层，热导就逐渐下降。原子层数达到10层后，引入中间层的系统的界面热导比平滑界面的热导降低了29%。原子混合层为2层时，系统的热导达到最大值。模拟结果表明，在2种高度不匹配的材料之间插入原子混合层，可以显著改善跨Si/Sn界面的热传输。

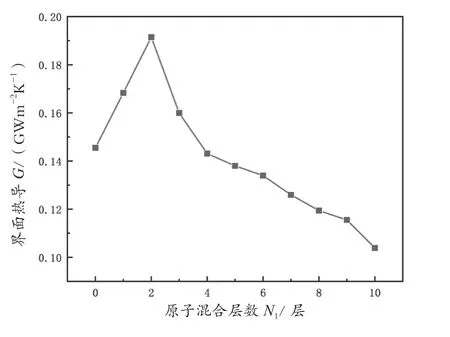
图5 界面热导随混合层厚度变化图

研究人员计算了系统中界面热导与温度之间的关系，计算结果如图6所示。结果表明，随着温度的升高，所有参与模拟的系统的界面热导都先呈上升的趋势，然后呈下降的趋势。当温度升至300 K时，引入2个原子层的原子混合层的系统的热导达到最大值。随着温度的升高，原子的振动能量会增加，由于在声子散射Umklapp的过程中，声子散射会增强;因此，随着温度继续升高，系统的界面热导会进一步降低。

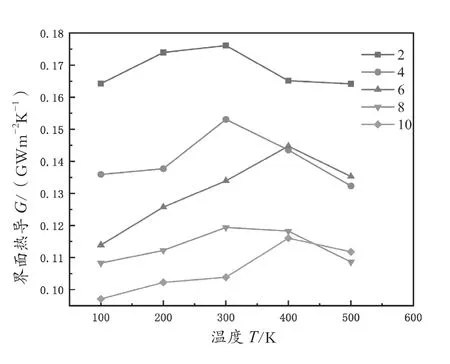
图6 不同混合层数界面热导随温度变化图

针对引入了2层原子混合层的系统，分别选取界面以及两侧的Si、Sn原子部分进行声子态密度计算（PDOS）。由于研究人员发现界面两侧固体表面和中间层中的原子主要以低于20 THz的频率振动，因此只取了频率小于20 THz的态密度。绘制出的PDOS如图7所示。此外，研究人员还绘制了不同混合层的系统态密度图（如图8所示）。

从图8中可以看出，内部的声子态密度（PDOS）受厚度变化的影响较小。随着系统内混合层厚度的增加，混合层PDOS中的声子模式会略微向低频方向迁移，并且PDOS曲线的频宽会呈现出增大的趋势。图6中，原子混合层的PDOS与Sn结构PDOS的重叠面积大于Si结构和Sn结构PDOS的重叠面积。较大的PDOS重叠面积表示非弹性声子散射会增加界面处的热传输[10]。

图5中，引入双层原子混合层结构的热导明显高于单层原子混合层结构的热导。研究人员猜测热导的提高是因为中间层与Sn结构DOS的重叠面积有所提高。对单原子层或两原子层的中间层来说，两侧的原子结构和中间层相互作用主导着层中原子的运动。随着中间层厚度的增加，层与层之间的相互作用变得越来越重要。因此，双层原子混合层的DOS频宽变得稍微宽一些（如图9所示）。单层原子混合层的DOS相对双层来说更锐利和狭窄，这应该归因于其强大的约束效应。较宽的DOS增大了中间层DOS与两侧原子结构DOS的重叠面积，增强了原子混合层与Si原子结构和Sn原子结构之间的非弹性声子散射，从而略微提高了界面处的声子热输运[10]。然而，同时弹性界面散射可能会随之减少。因此，热导在2原子层的厚度处达到最大值，然后热导随厚度增加而减小（如图5所示）。

图7 2层混合层系统态密度图

图8 不同混合层系统态密度图

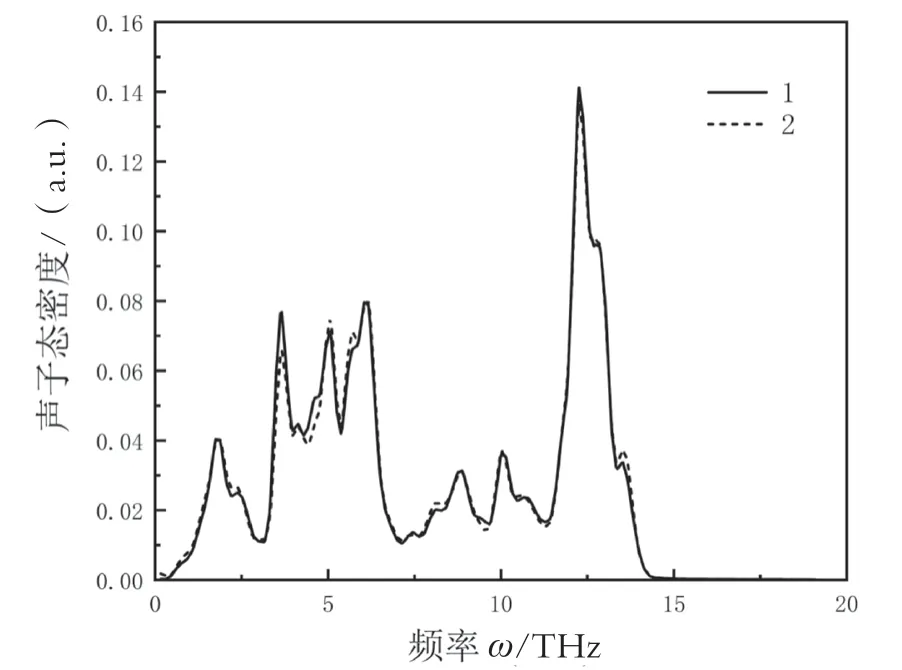
图9 双层以及单层混合层态密度图

综上所述，可以得出结论，随着原子混合层厚度的增加，系统的DOS不会改变太多。中间层的DOS分布与Sn结构DOS之间的重叠面积会出现略微增加的情况。研究人员认为弹性界面散射不可能是引起2层和单层中间层之间的热导增加的原因。因此，将界面热导的增加归因于非弹性声子界面散射的微弱增加。随着引入界面的原子混合层层数增大，热导在层数高于2之后逐渐降低。研究人员认为该现象可以归因于界面处的弹性散射与非弹性散射之间的竞争。尽管根据图6和图8已经可以证明，引入双层原子混合层能够增加非弹性界面散射，从而增加热传导；但是随着中间层厚度的增加，界面处的弹性散射逐渐减小。非弹性散射的增加已经不再能与弹性散射的减小相抗衡，从而出现了热导在中间层厚度超过2层之后减小的现象。

为了探究声子活动（尤其是声子的局域化程度）以及声子对不同系统热导的影响，研究人员使用公式（8）计算了声子的参与率。声子参与率可以测量给定模式下的原子比率，并可以用O （1/N）和O （1）分别表示局域化和非局域化下的声子模式。声子参与率可以详细地展示每种声子模式的局域化信息。图10分别展示了当系统界面处原子混合层数为2、6和10时的声子参与率，参与模拟的样本长度为23.844 nm，温度设置为300 K。研究人员认为PPR＜0.4时，证明声子发生了局域化现象。结果表明，无论考虑低频声子还是高频声子，随着原子混合层厚度的增加，系统的PPR逐渐降低。随着混合层厚度的增加，越来越多的声子显示出声子局域化的特征。而声子对热传输的贡献主要来自非局域化声子，而不是局域化的声子[11]。与预期结果相同，由于存在声子局域化的现象，因此包括10个原子混合层的系统的界面热导通常比其他2个系统都要小。

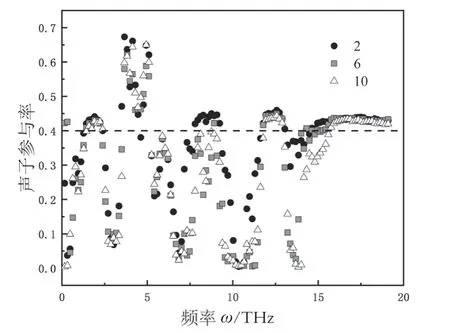
图10 混合层声子参与率

5 结语

该文在纳米结构的界面处构建了1种能够有效提高界面热导的原子混合层结构，与光滑界面相比，该界面的热导提高了31.6%。采用非平衡分子动力学方法，分别模拟不同尺寸和不同温度下该结构的热导的变化，并利用声子态密度以及声子参与率对该结构能够大幅度提高热导的原因进行分析。为高散热硅基纳米材料的开发研究提供了一定的指导，对高散热半导体材料的制备和发展有重要意义。