基于滑移线场理论的巷道底鼓机理与防治技术研究

2021-05-25程辉赵洪宝徐建峰秦逢缘张一潇胡林枫

古地理学报 2021年3期

程辉，赵洪宝，徐建峰，秦逢缘，张一潇，胡林枫

中国矿业大学(北京)能源与矿业学院，北京 100083

随着我国煤炭资源开采逐渐由浅部转入深部，在高应力作用下巷道发生底鼓的可能性大大增加。巷道底鼓直接影响矿井的正常生产，不合理的底鼓治理技术也会耗费大量的人力、物力。研究巷道底鼓发生机理以及防治技术对于保障煤矿正常生产具有重要意义。

针对巷道底鼓发生机理，诸多学者进行了较为深入的研究。柏建彪等[1]运用FLAC3D数值模拟软件确定了巷道底鼓发生时底板存在着“两点三区”，即零位移点、零应变点，并以这两点将采动巷道底板从上向下分为拉应变上升区、拉应变压缩区、压应变压缩区；孙利辉等[2]认为深部巷道强烈底鼓是由高地应力、岩石内黏土矿物遇水膨胀、支护结构不合理等综合因素影响造成的，并通过相似模拟试验确定了底板锚索束+底板浅部、深部注浆的综合底鼓控制技术；孙晓明等[3]基于欧拉公式，利用压杆稳定理论、莫尔库仑准则和挠曲破坏力学模型，分析了不同层状岩体巷道变形破坏机理；曹平等[4]将底板受水平应力挤压变形简化为受轴向力作用的板状材料力学模型，运用弹性力学得出底板岩层应力状态；王卫军等[5]认为回采巷道两帮煤体的强度对巷道底鼓产生重要影响，煤体强度较大的回采巷道两帮破坏范围较小，底板鼓起的范围随之减小，因而底鼓量较小，反之底鼓量较大，并在工程实践中得以验证；李传明等[6]认为薄分层软弱底板巷道围岩在支护体作用下形成“组合岩梁”，破坏形式从单层压曲破坏转变为整体“组合岩梁”破坏；康红普等[7]运用弹性薄板理论对巷道底鼓进行了分析，认为巷道发生底鼓的主要原因是底板受到水平应力挤压而发生挠曲；江东海等[8]运用3DEC软件建立了复杂节理岩体巷道模型，深入探究了复杂节理岩体巷道非对称底鼓机制并给出相应控制对策；王晓卿等[9]以潘一东矿带式输送机大巷为研究对象，采用数值模拟研究了巷道底鼓机理，并提出以端锚锚索束为主的底鼓控制方案；李新旺等[10]针对不同侧压系数条件下巷道底板变形特征、底板岩层破坏规律进行了深入分析。

前人研究成果对巷道底鼓防治具有一定的指导作用，但对于滑移型底鼓发生机理与防治技术的研究，仍有待于深入开展。本文基于前人研究成果，采用滑移线场理论深入探究巷道底鼓发生机理，并以山西焦煤回坡底煤矿1021巷为工程背景，揭示其底鼓机理并提出针对性的底鼓防治技术，最终进行现场实践。本文研究内容对煤矿巷道底鼓机理与防治技术研究具有参考与借鉴作用。

1 巷道底板滑移线场模型

1.1 理论模型

井下巷道开挖后，围岩应力重新分布，巷道两帮形成支承压力，若底板岩性较软，巷道底板会在两帮支承压力作用下形成滑移线场[11]，其简化力学模型如图1所示。

图1 底板滑移线场模型

图1中，L为巷道两帮支承压力作用范围；b、h分别为巷道宽度与高度；v为底板速度场任意一点的速度。

假设巷道底板的塑性滑移破坏符合Mohr-Coulomb准则且巷道底鼓问题属于平面应变问题，根据滑移线场理论，可知巷道两帮底板的极限承载力[12]为

(1)

式中，φ为底板岩层内摩擦角；c为岩层黏聚力；q为底板极限承载力。

假设巷道两帮支承压力峰值为KγH，此时，巷道底板发生塑性滑移的临界条件为

(2)

式中，K为巷道两帮支承压力峰值系数；γ为岩石容重；H为埋深。

1.2 底板滑移线应力场

根据应力场巷道底板滑移场可分为3个区域，分别为主动应力场、过渡应力场和被动应力场。以图1为例，ABC区域为主动应力场，BCD区域为过渡应力场，BDE区域为被动应力场。

根据滑移线场理论，滑移线可分为α族和β族，在BDE区域中，α线和β线均为直线，因此，BDE区域根据滑移线场基本性质可知，该区域属于均匀应力场，根据Mohr-Coulomb准则可得其平均应力为

(3)

在BCD区域，该区域为蜕化的Riemann问题，B点为应力间断点，且滑移线不全为直线，滑移线的基本性质失效，此时不能通过D点处的应力状态得出该区域内所有的应力状态。该区域内所有的α线均为直线，β线是同心对数螺线。已知在BCD区域中，C点的应力状态[12-13]为

(4)

式中，μ为α线与β线之间的夹角，且μ=π/4-φ/2。

结合扇形滑移线场中的平均应力关系式可得BCD区域中的任意一点应力状态为

(5)

式中，φ为β线上任意一点与BC线之间的夹角。

在ABC区域，该区域内所有的α族和β族均为直线，因此ABC区域同样为均匀应力场。所以该区域内的应力状态即为C点应力状态，即

(6)

对比底板应力场应力可得

(7)

由式(7)可知，在巷道底板无支护条件下，越靠近两帮下方的底板区域，其应力集中程度越大；远离两帮的底板区域，应力集中程度越小。该规律符合现场实际规律。

1.3 底板滑移线速度场

ABC区域因滑移线均为直线，因此属于均匀速度场，该区域内的合速度方向为垂直向下，在该区域内沿着α线和β线的速度为

(8)

在BCD区域，沿着α线和β线的速度[12-13]为

(9)

式中，θ为某点主应力切线方向与水平方向的夹角。

在滑移线场中，滑移线即为速度间断线，所以沿着β线的速度与滑移线之间存在大小为φ的夹角，其速度矢量方向如图1所示。

BDE区域与ABC区域相同，亦为均匀速度场，该区域速度场[12-13]为

(10)

同样，β线的速度方向与滑移线之间存在大小为φ的夹角。式(10)仅考虑单侧巷帮作用下的速度场。两帮作用下，BDE区域水平方向速度相互抵消，而垂直方向速度为两帮作用下速度垂直分量的叠加。因此，BDE区域的垂直方向速度为

(11)

通过上述对滑移线场的理论分析可知，底板ABC区域在巷道两帮支承压力作用下，速度方向向下，呈下沉趋势。BCD区域岩体以B点为旋转点向巷道内部转动，BDE区域由于受到BCD区域岩体的旋转挤压，产生了向上的速度，从而发生底鼓现象。

采用FLAC3D对巷道底板速度场进行模拟验证，因巷道变形属于平面应变问题，数值模型尺寸设计为长50 m、高35 m、宽2 m。模型总计62 000个单元，75 978个节点。模型包括6个煤岩层，从下往上依次是中细砂岩8 m、泥岩7 m、煤层6 m、油页岩5 m、中细砂岩5 m、粉砂岩4 m，如图2所示。模型顶部施加垂直应力20 MPa，为自由边界，底部以及左右前后进行位移约束，为固定边界。模拟采用Mohr-Coulomb模型进行计算。运算平衡后的模型沿煤层底板开挖4 m×3.5 m(宽×高)的矩形巷道，再次运算至平衡。各岩层具体物理力学参数见表1。

数值模拟结果如图3所示，由图3可以看出，两帮下底板1区域速度竖直向下，导致2区域的岩体产生旋转的速度矢量，3区域岩体在两侧岩体的旋转挤压下发生底鼓现象，产生垂直向上的速度(图3中红色箭头代表底板不同区域整体的速度方向)。可以看出，数值模拟结果与理论结果保持一致，验证了理论分析的正确性。

图2 数值模型岩层分布

表1 岩层物理力学参数

图3 滑移线速度场模拟结果

2 工程实例

2.1 工程背景

山西焦煤回坡底煤矿主采10号与11号煤层，煤层平均厚度10号为2.65 m、11号为3.2 m，两层煤之间平均间距为6.62 m，属于近距离煤层开采。本文所研究巷道为东一采区11-102工作面1021运输巷。1021巷所处位置如图4所示。

图4 工作面与巷道位置布置图

1021巷宽4.6 m、高3.3 m、埋深560 m。根据矿方地应力报告显示，1021巷所受垂直应力约为14 MPa，整条巷道平均侧压系数约为1.5。其上方为10号煤层10-102工作面，该工作面现场监测时期已全部采空。与10-102工作面相邻的是10-103工作面，正处于回采阶段，随着10-103工作面不断推进，两个工作面之间的区段煤柱逐渐演化为孤岛煤柱，煤柱平均宽度为25 m，1021巷与煤柱边缘距离10 m。1021巷直接底为0.8 m铝质泥岩，基本底为3 m泥岩，底板为裸露状态，无任何支护措施。巷道布置在采空区下方的卸压区，原本应有利于巷道维稳，但在实际现场中发生了较为严重的底鼓现象，最大底鼓量达到1 m。回坡底煤矿面对严重的巷道底鼓现象，反复采用卧底法进行治理，但该种方法治标不治本，巷道底鼓现象并没有得到解决。同时，还消耗了大量的人力、物力，严重影响矿井的正常生产。

2.2 底鼓机理研究

从图4可知，10号煤层孤岛煤柱由于两侧采空，必然会形成高支承压力，因此煤柱下方底板会形成一定程度的应力集中，造成1021巷围岩应力环境的改变，导致巷道出现严重的底鼓现象[14]。基于滑移线场理论已知巷道两帮支承压力分布对巷道底鼓有直接影响，因此，探究巷道两帮支承压力分布对掌握1021巷底鼓机理有重要意义。

1021巷两帮支承压力由巷道开挖引起的围岩应力和煤柱引起的应力集中叠加而成。已知巷道开挖引起的围岩应力[15-17]为

(12)

式中，R为巷道几何当量半径；r为围岩距巷道中心的距离；θ为围岩单元与水平方向应力的夹角；σr、σθ、τrθ分别为巷道围岩单元所受到的径向应力、切向应力、剪应力。

孤岛煤柱支承压力在10号煤层底板引起的应力集中可由弹性力学半平面无限体计算得到，其基本公式[18-20]为

(13)

式中，σx、σy、τxy分别为孤岛煤柱在底板引起的水平应力、垂直应力与切应力；λ为侧压系数；ξ为底板任意一点处微单元与原点的距离。

为准确探究孤岛煤柱支承压力分布规律，采用FLAC3D模拟10号煤层孤岛煤柱的支承压力分布情况，建立如图5所示的数值模型。模型尺寸为474 m×100 m×135 m(长×宽×高)，共计5 498 400个单元，5 663 676个节点。模型顶部施加12.25 MPa的应力，侧压系数设置为1.5，模型底部设置垂直方向位移约束，为固定边界，模拟采用Mohr-Coulomb模型进行计算。模型初始平衡后开挖10-102与10-103工作面，工作面长度均为200 m，开挖后继续运算直至模型重新平衡。岩层力学参数见表2。

图5 数值模拟计算模型

根据模拟结果，提取孤岛煤柱支承压力分布结果，如图6所示。

图6 孤岛煤柱支承压力分布结果

基于图6，取孤岛煤柱支承压力的应力增量进行数学拟合，得到支承压力分段拟合方程；煤柱两侧采空区支承压力，根据现场经验假设从煤柱边缘至采空区内部10 m范围内达到原岩应力状态，便可得到其应力增量函数。将函数分别代入式(13)中叠加，计算得到不考虑巷道开挖情况下孤岛煤柱在底板引起的垂直应力分布，如图7所示。

图7 孤岛煤柱引起的底板垂直应力分布

表2 回坡底煤矿岩层物理力学参数

由图7可以看出，孤岛煤柱应力集中导致底板垂直应力显著增大，且以煤柱中心线为轴呈对称性分布；距离煤柱边缘越远，垂直应力越小；1021巷两帮支承压力分布，如图8所示。

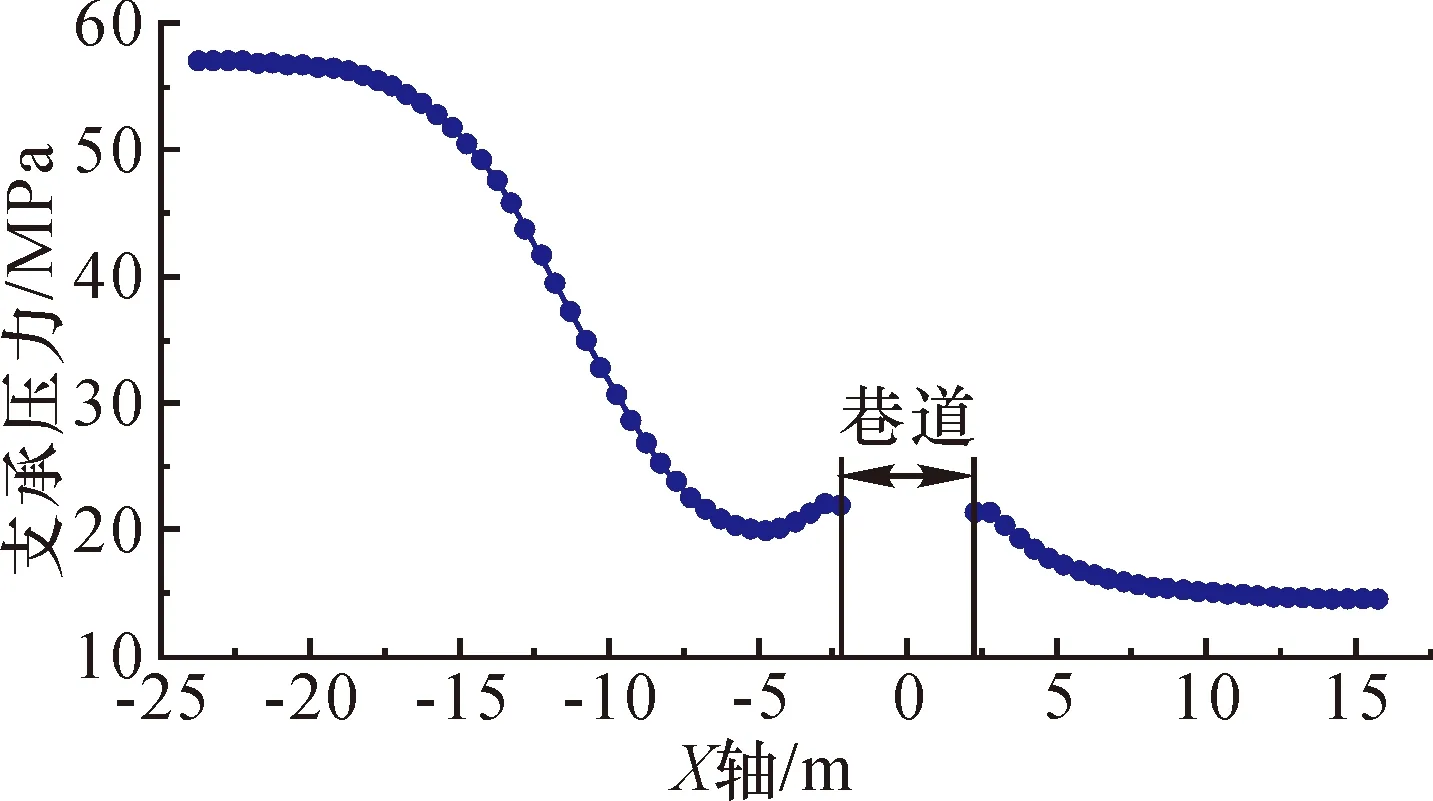
图8 巷道两帮支承压力分布规律

由图8可以看出，巷道两帮支承压力呈现明显的非对称分布，靠近煤柱一侧巷帮支承压力较大，远离煤柱一侧支承压力较小，两者数值上相差4.07倍，非对称性的支承压力分布与1021巷底鼓特征有直接关系。

已知巷道底板在两帮支承压力作用下产生滑移线场，且支承压力越大，底板滑移线场范围越广，速度场也就占据主导优势。从1021巷两帮支承压力分布情况来看，靠近孤岛煤柱一侧支承压力远大于另一侧，若考虑应力增量在巷道底板引起的滑移线场，远离煤柱一侧巷帮支承压力在底板引起的滑移线场可以忽略。因此，1021巷底板滑移线场模型如图9所示。

图9 1021巷底板滑移线场模型

1021巷底板滑移线场主要由靠近煤柱一侧巷帮的高支承压力引起，底板滑移线同样存在主动区(ABC区域)、过渡区(BCD区域)、被动区(BDE区域)，ABC区域由于高支承压力作用，其速度场垂直向下，挤压过渡区BCD区域使该区域以B为基点，向巷道内部转动并挤压BDE区域，BDE区域速度方向与滑移线夹角为φ，其速度场整体方向指向远离煤柱一侧巷帮。理论分析结果与FLAC3D数值模拟结果基本保持一致，验证了理论分析的正确性。

基于上述分析可知，1021巷底鼓现象将会呈现出明显的非对称性分布，远离煤柱一侧底板底鼓量较大，靠近煤柱一侧底鼓量较小。该结论与1021巷现场实际情况相吻合。因此，针对1021巷底鼓防治技术，应考虑其非对称性分布特征。

2.3 底板破坏深度研究

巷道底板破坏深度是底鼓防治技术确定的重要依据，假设巷道底板破坏满足Mohr-Coulomb准则，其基本原理如图10所示。

图10 Mohr-Coulomb准则

由图10可知，若知道底板任意一点应力状态，便可确定其莫尔圆，τmax为该单元的最大剪应力，τr为单元实际的抗剪强度。若τmax<τr，则认为单元不发生破坏；反之，则发生破坏。因此，定义底板破坏准则为

(14)

图8中已知1021巷两帮支承压力分布，以巷道为中心建立直角坐标系，取两帮支承压力增量进行拟合，便得到分段拟合方程；底板黏聚力c=2.8 MPa；内摩擦角φ=28°。在matlab软件中将分段拟合方程代入式(13)计算得到巷道底板应力分布，再将底板黏聚力与内摩擦角代入式(14)，计算得到巷道底板破坏云图如图11所示。

图11 1021巷道底板破坏云图

由图11可以看出，巷道在两帮支承压力作用下，1021巷底板最大破坏深度可达4.3 m，该计算结果与回坡底煤矿底板钻孔窥视结果较为吻合，一定程度说明了理论解算的正确性。

3 底鼓防治技术研究

针对1021巷非对称底鼓特征，结合回坡底实际情况，将巷道底板由原来的无支护方案调整为单体锚索平行布置的非对称支护，支护设计如图12所示。该支护方案中，锚索采用该矿原先使用的φ18.9 mm×6 000 mm高强度弹性松弛钢绞线，已知底板最大破坏深度为4.3 m，因此该锚索支护具有较好的着力点。同时，锚索重点在巷道底鼓量较大一侧进行支护，间排距1 200 mm×1 800 mm，巷道中心线处锚索垂直底板支护，远离巷道中心线处的锚索则与垂直方向之间夹角约为20°，通过锚固作用抵抗巷道底板滑移。