基于数值计算的测斜仪监测误差分析
2021-05-25赵振宇
赵振宇
(贵州省交通规划勘察设计研究院股份有限公司,贵州 贵阳 550038)
边坡位移监测是判断边坡稳定性的重要方法。近年来,测斜仪在边坡深部位移监测中得到广泛应用[1-5]。马水山等[1]通过对国内几个典型滑坡体深部变形监测实例的分析,认为钻孔测斜仪具有精度高、量程较大、性能可靠等特点;陈开圣等[3]将测斜仪应用到滑坡变形监测中,并与钻探结果进行对比,对滑动面的分布情况、滑动机制作出判断,说明测斜仪在滑坡监测中的应用是可行的;彭纪超等[4]利用RQBF-698B型钻孔测斜仪对贵州省化乐煤矿三井区的滑坡带进行监测,总结出一种提高钻孔测斜仪监测效率的方法;黄飞澜等[5]的研究表明测斜仪可检测地基不同深度处的侧向水平位移,较好地反映了地基土体内可能存在的滑裂面的位置和滑动方向。
测斜仪在边坡变形监测中会存在一定误差,使得监测结果偏离真实值,当误差过大则会使技术人员对边坡的变形做出误判。针对测斜仪误差的研究已有很多[6-12],如:方大勇[6]针对边坡长期监测中出现的部分测斜数据离散性较大、位移方向不合理的问题,提出探头角度定位旋转误差是造成现场测量结果误差的主要原因;李国维等[7]基于测斜仪工作原理,分析了滑动式测斜仪在使用过程中的误差成因,针对测斜仪零点数据漂移问题,分别从零点漂移量恒定和零点漂移量变化两种情况导出了对应的修正公式,基于统一基准线修正法(UBM),专门针对深孔测斜情况,应用标量和代替矢量和(以曲代直)简化思想解决了零点漂移问题;乔美英等[10]基于递推最小二乘的误差补偿数学模型,采用椭球拟合法、点积不变法和旋转平面拟合法的联合校正方法对随钻测斜仪进行误差补偿校正,并对随钻测斜仪进行数值仿真和双轴转台实验,用联合校正方法对实验数据进行误差补偿校正,校正后测量精度满足随钻测斜仪要求;徐想[11]在三维正交传感器基础上推导倾斜角及方位角数学模型和计算公式,然后从理论上构建重力加速度计静态的数学模型以及加速度计存在安装误差时的数学模型,利用ADAMS动力学仿真软件构建了重力加速度传感器精确安装和存在安装误差时测量系统的物理模型。
以上针对测斜仪误差所作的研究大多是针对监测仪器本身的误差、环境引起的误差和人为误差进行的,也有学者研究了监测曲线所产生的误差问题。就测量原理来说,测斜仪对深部水平位移的测量是根据一些有限的监测点的角度变化来计算变形曲线的水平位移值,这种以点代线的测量方法本身就存在误差。因此本文尝试从测斜仪测量原理和数值分析角度分析测斜仪测量误差产生的原因。
1 深部测斜仪原理
深部位移测斜仪监测原理为:根据仪器中铅锤受重力影响,其方向为垂直状,测量出测试管轴线与垂直方向的夹角,计算出钻孔内各个测点的水平位移。其基本原理如图1所示。
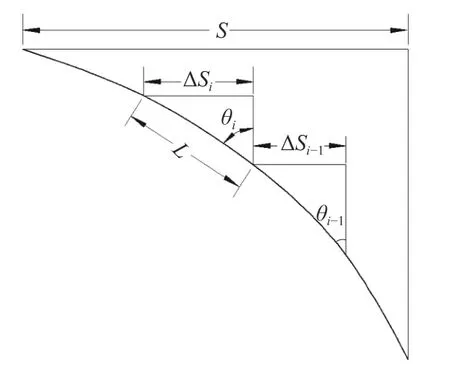
图1 测斜仪监测原理示意图Fig.1 Schematic diagram of the inclinometer monitoring principle
在实际监测中,一般先要在边坡钻孔埋设测斜管,利用测斜管中内径两组互成90°的导向槽,将测斜仪顺导向槽放入测斜管内,逐段(人工监测时标准长度为50 cm,也可自行确定)测量。当边坡由于滑动产生倾斜变形时,通过安装在测斜仪内的传感器测出该段的角度变化量,利用该段长度和角度变化量计算出该段的水平变形值。对每段水平变形值进行计算并累加,即可获得钻孔内全长范围的水平位移值。其计算方法为:
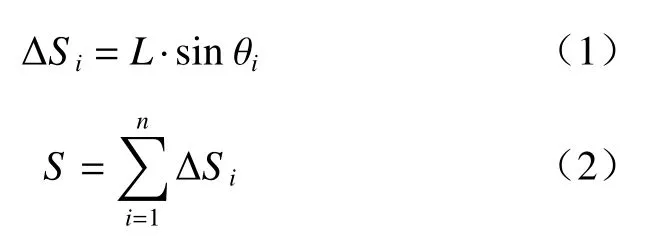
式中:L——测量段标准长度/m;
ΔSi——第i段水平位移变形值/m;
θi——第i测量段倾角/(◦);
S——水平变形总位移值/m。
2 深部测斜仪测量原理数值分析
深部位移测斜原理是利用测量孔内各段测点夹角的变化,从而计算水平位移,其数学计算方法等同于常微分方程数值解中的Euler法。Euler法解常微分方程的解法为:
有一常微分方程:
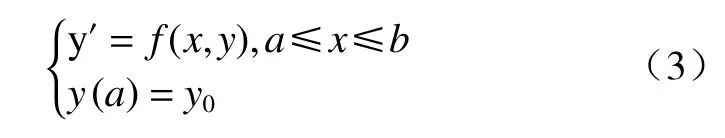
当f(x,y)对y满足Lipschitz条件,求解式(3)一种最简单的方法为将节点xn的导数y′(xn)用差商代替,由此式(3)可近似写为:
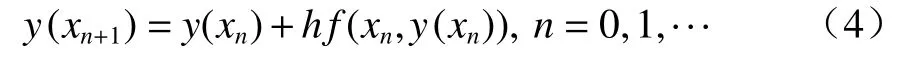
从x0开始计算y(a)=y(x0)=y0,由式(4)可得y(x1)≈y0+hf(x0,y0)=y1,再将y1≈y(x1)代入式(4)右端,得到y(x2)近似为y2=y1+hf(x1,y1),一般写成:
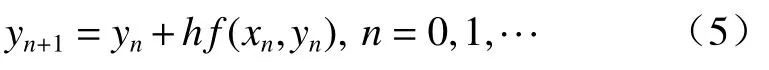
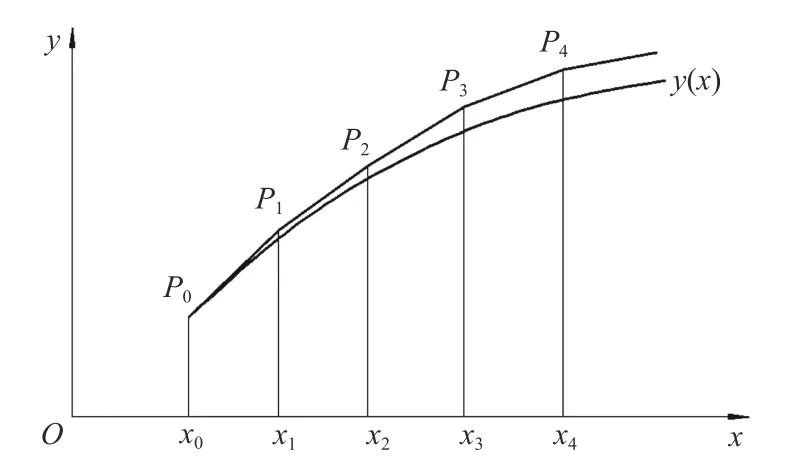
图2 Euler法的几何意义示意图Fig.2 Schematic diagram of the geometric meaning of the Euler method
Euler法的几何意义如图2所示。式(3)的解曲线y=y(x)是从点P0(x0,y0)出发,以f(x0,y0)为斜率作一段直线,与直线x=x1交点于P1(x1,y1),显然有y1=y0+hf(x0,y0),再从P1出发,以f(x1,y1)为斜率作直线推进到x=x2上的一点P2,其余类推,这样得到解曲线的一条近似曲线,它就是折线。由Euler法解法和几何意义可知,若将图2的坐标轴原点O移到P0点,得到图3。可以认为函数曲线y(x)是钻孔水平变形曲线,其中原点O为深部位移内滑面,通过深部位移测斜仪,可以测出P1、P2、······各点的变化夹角,从而得出该点的斜率值,通过计算,折线为测量的位移变形曲线。由于钻孔水平位移的变形量和孔深相比,其值要小很多,其夹角变化的值也非常小,因此,可认为深部位移测量中各段的标准长度L和Euler法中的步长h相等。深部测斜结果中斜率值与Euler法中f(xn,y(xn))相对应,数值计算结果中y(xn)与对应。由此可知,由深部位移监测计算的变形值,就是常微分方程的Euler法数值解。
3 深部测斜仪测量误差与分析
3.1 深部测斜仪测量误差
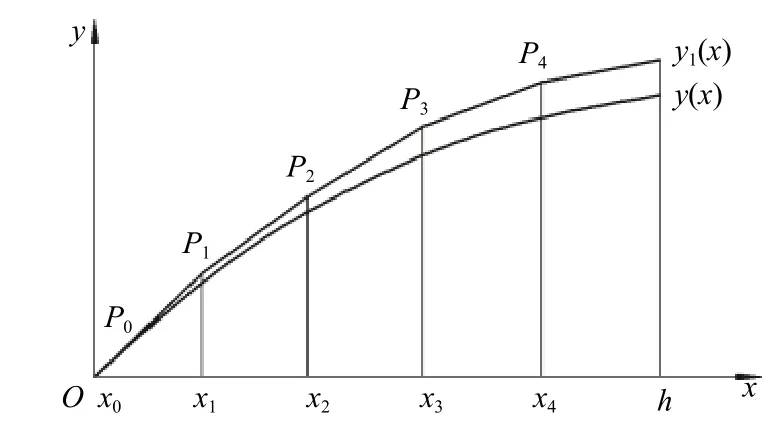
图3 Euler法的几何意义示意图(原点偏移)Fig.3 Schematic diagram of the geometric meaning of the Euler method(Origin Offset)
由第2节的讨论结果可知,可用常微分方程的Euler法数值解分析深部测斜仪测量结果误差。
Euler法也可利用y(xn+1)的Taylor展开式得到:

其中,由于y′(xn)=f(xn,yn),与式(5)相比,Euler法与准确解相差,那么就是Euler法的局部截断误差,也即深部位移测量值的各段误差,整体误差就是各段误差的累计总和(T),具体见式(7):
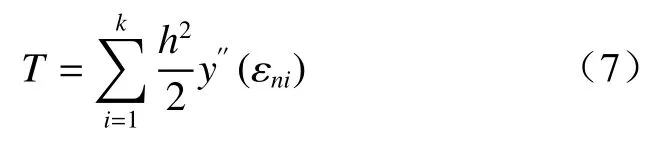
3.2 深部测斜仪测量误差分析
(1)测量初值对误差的影响分析
由图3和式(6)可知,深部位移测量值的计算在初始值y0的基础上进行,y0值的准确性决定了测量值的合理性,因此需要保证初值为0或为固定值,即要求深部位移监测孔要深入滑面以下。
(2)测量分段长度对误差的影响分析
由式(7)可得,深部位移测量值的误差大小与k、h和y′′(εni)有关。其中k为深部位移测量孔的分段个数,h为每个分段的长度。在总深度确定的情况下,k和h关系如下:

式中:H——测量孔总深度/m。
把式(8)代入式(7)中,得
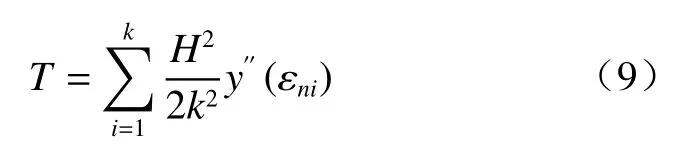
由式(9)可见,在监测孔深为定值的情况下,监测误差与k和ni) 有关。由于在每个测量段内是在一个区间范围内变化的值,不便于分析,因此暂定取所测量区段内的最大值,设这个最大值为y′′(εn),那么式(9)就变为:
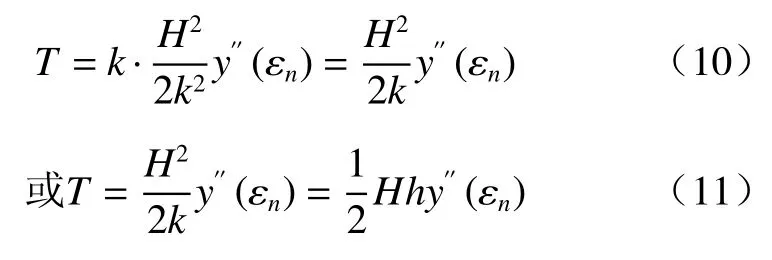
由式(10)或式(11)可知,在总深度一定的情况下,总误差随着测量分段个数的增加或测量分段长度的减小而减少,呈一次线性关系。当测量分段个数k→∞(或分段长度h→0)时,总误差趋近于0。
所以,如果需要提高测量精度,就应增加测量分段个数或减少测量分段长度。
(3)变形曲线形状对测量误差的影响分析
为了便于分析测量分段长度对测量结果的误差,假定y′′(εni) 为固定值,而在实际中,y′′(εni)是随变形曲线的形状而变化的。由于实际中变形曲线的形状比较复杂,y′′(εni)的值无法确定,因此本节仅对简单的曲线进行误差分析,并假定测量孔深和监测分段个数(或分段长度)为定值。
①y′′(εni)=0
当y′′(εni)=0,y′(εni)=c(c为常数),表明变形曲线的斜率为常数,即曲线为一直线,此时式(10)或式(11)等于0,表明监测数据误差为0。
②y′′(εni)≠0
当y′′(εni)≠0,y′′(εni)的大小取决于深部位移变形曲线的斜率变化,当y′′(εni)同号时,同号时一般y′′(εni)>0,由于位移变形曲线误差是累计误差,随着测量次数的增加,测量误差也累积增大。从孔底开始测量误差向孔顶依次增大,孔内顶部最后一次测量计算的数据误差最大。
另外,当y′′(εni)>0,表明曲线是凹形。由式(9)知,y′′(εni)越大,计算误差越大。说明监测变形曲线的凹形程度越大,监测计算误差越大,孔口的变形值也越大。这表明孔口变形越大时,监测数值的误差也越大。
4 监测曲线形状对误差的影响分析
在第3节分析结果可知,曲线形状对监测数值误差的影响较为复杂。以孔深为定值(假设为50 m),监测曲线分别为二次曲线和三次曲线条件下孔口变形和测量段数的不同进行误差分析。
4.1 二次曲线
设位移变形曲线为y=Ax2,x为孔深(50 m),y为孔口变形值,分别以不同孔口变形量和测量段长分析误差。
(1)孔口变形值
以孔口变形为0.5 m计算,把y=0.5、x=50代入曲线方程得A=2×10−4。假设测量段长h=0.5 m,则测量总段数k=100,得y′′=2A=4×10−4。
把上述结果代入式(10),得孔口误差为5×10−3m,即5 mm。由此可见,测斜仪测量的误差是较小的。依据上述方法,计算孔口水平位移在0.4,0.3,0.2,0.1 m时的误差,结算结果见表1,可知孔口水平误差随孔口变形值的减少而减少,误差约为1%。

表1 不同孔口水平位移下的计算误差Table 1 Errors under different orifice displacement
(2)测量分段长度
以孔口变形值为0.5 m,孔深为50 m,代入式(10)计算测量分段长度不同时的误差计算,结果见表2,可见误差随测量段长的增大线性增大。

表2 不同测量分段长度下的计算误差Table 2 Errors under different length of the measuring section with conic curve
4.2 三次曲线
y=Ax3
设位移变形曲线为,x和y意义和取值、测量段长(h=0.5 m)和总段数(k=100)均同4.1节。(1)孔口变形值
把y=0.5、x=50代入y=Ax3,得A=4×10−6。
因y′′=6Ax,则y′′(εn)=6Aεn,此时,εn是一个不定的数值,以最大值来考虑计算出来的误差偏大,趋于保守。取εn=50,y′′=1.2×10−3,
把上述结果代入式(10)得孔口误差为15 mm。依据上述方法,计算孔口水平位移在0.4,0.3,0.2,0.1 m时的误差,结果见表1。
(2)测量分段长度
用式(10)计算孔口变形值为0.5 m、孔深为50 m,不同测量分段长度时的误差,结果见表2。
由表1和表2可知,在相同条件下,三次曲线的误差大于二次曲线的误差,原因在于数值分析中三次曲线的y′′(εni)的值比二次曲线的大,所以造成监测误差增大。说明在深部位移监测中,曲线变形弯曲程度越大,其监测误差越大。
5 结论
(1)深部位移监测初始值须为0或固定值。
(2)监测变形误差与监测曲线的形状有关。监测位移曲线为直线时,误差等于0;监测位移曲线为曲线时,误差的大小根据位移曲线的形状来确定:当监测曲线为凸曲线(或凹曲线)时,其变形程度越大,误差越大;当变形曲线为单一的凸曲线(或凹曲线),监测测量误差为累计误差,从孔底向孔口误差依次增大。
(3)监测变形误差与测量分段长度有关,测量分段长度越小,测量误差越小,当测量段长趋近于无穷小时,误差为0。
(4)对于相同形状的监测曲线,孔口变形值越大,监测测量误差越大。
