使用长短期记忆人工神经网络进行花岗岩变形破坏阶段的判别
2021-05-25陶雪杰徐金明王树成王亚磊
陶雪杰,徐金明,王树成,王亚磊
(1.上海大学土木工程系,上海 200444;2.中铁十七局集团有限公司,山西 太原 030006)
岩石是一种典型的颗粒材料,通常是由不同成分组成(如花岗岩通常由石英、黑云母和长石等组成)。岩石的变形破坏过程与这些成分的变化过程密切相关。因此,判别岩石所处的变形破坏阶段对分析岩石变化过程和物理力学性质具有重要的理论意义和实用价值。
使用数字图像处理技术研究岩石的变形破坏过程,已经取得了很多进展。如在使用图像处理技术方面,陈中一等[1]获得了单轴压缩条件下花岗岩中不同组分长度和面积的变化过程,Rigopoulos等[2]分析了岩石特征对裂隙萌生和扩展的影响,Lin等[3]结合傅里叶变换得到了岩石中的位移变化特征,Akesson等[4]研究了单轴循环荷载作用下花岗岩中不同微观裂隙的变化情况,孙皓等[5]探讨了花岗岩中不同矿物成分的变化特征,张岩等[6]分析了花岗岩中细观组分的定向性变化特征,Han等[7]以裂缝为目标追踪岩石中裂纹的运动,徐金明等[8]使用粒子图像测速技术得到了石灰岩裂隙的萌生扩展过程和数字特征参数变化过程,刘希康等[9]使用基准图像与对比图像相对熵研究了花岗岩的损伤演化特征。
近年来,一些学者尝试使用长短期记忆神经网络(Long-Short Term Memory Neural Network,LSTM-NN)来解决土木工程问题。如,刘雪燕等[10]提出一种基于LSTM-NN和注意力机制结合的矿山安全事故分类方法,对矿山事故进行了安全等级分类,曲星宇等[11]使用LSTM-NN实现了磨矿系统故障的智能化诊断。在建筑工程领域,Rashid等[12]使用LSTM-NN和时序数据对施工设备活动进行识别,Zhang等[13]利用LSTMNN建立两级结构来检测轨道裂纹的声发射信号。在交通工程领域,付文秀等[14]利用LSTM-NN对列车测速测距设备故障进行分类对比得出LSTM-NN的分类效果优于全卷积神经网络,Gao等[15]利用LSTM-NN和门控循环单元(Gated Recurrent Unit,GRU)对隧道掘进机(TBM)的运行参数进行了实时预测,Zhou等[16]提出了一个包含小波变换噪声滤波器、卷积神经网络特征提取器和LSTM预测器的预测框架,用于确定盾构机的掘进姿态和位置。
目前,外荷作用下岩石所处变形破坏阶段的传统确定方法多使用定性标准,对变形破坏过程中岩石不同组分(尤其是裂隙)变化过程及其定量描述重视不够。由于室内试验视频具有很好的等时距数据分布特征,可以将数字图像处理技术和LSTM-NN模型结合起来分析外荷作用下岩石的变形破坏阶段。本文拟使用单轴压缩条件下花岗岩试样的室内试验视频图像,在分析岩石变形破坏阶段、提取不同组分数字特征参数基础上,建立基于LSTM-NN模型的岩石变形破坏阶段分类网络,分析主要模型参数对分类准确性的影响,使用所建模型来判别岩石所处的变形破坏阶段,这对分析岩石变形破坏机理和变化特征具有一定的参考价值。
1 花岗岩变形破坏阶段的确定
1.1 花岗岩单轴压缩试验视频图像处理
花岗岩试块取自甘肃省玉门市北山地区,将其制成50mm×50mm×100mm大小的试样,通过打磨使试样断面平整度小于0.02mm。使用邦威200 t伺服压力机进行单轴压缩试验,使用佳能600 D摄像机在距试件约100 cm处拍摄试验视频,得到记录格式为MOV的试验视频图像。
研究时共获得了6个试验视频。限于文章篇幅,下面以1号试验视频为例(下同),说明视频中单帧图像处理方法与岩石变形破坏不同阶段的分析方法。
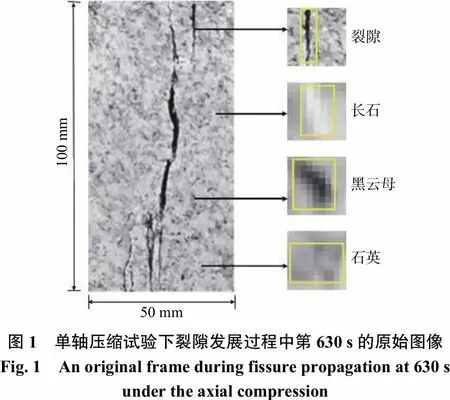
试验视频每秒提取1帧,共提取岩石变形破坏过程的630帧图像。采用传统矿物鉴定技术和点选法确定花岗岩中不同位置的组分类型。图1是1号试样中裂隙发展时第630 s的原始图像,图中标出了不同组分类型的分布情况。
1.2 花岗岩变形破坏阶段的划分
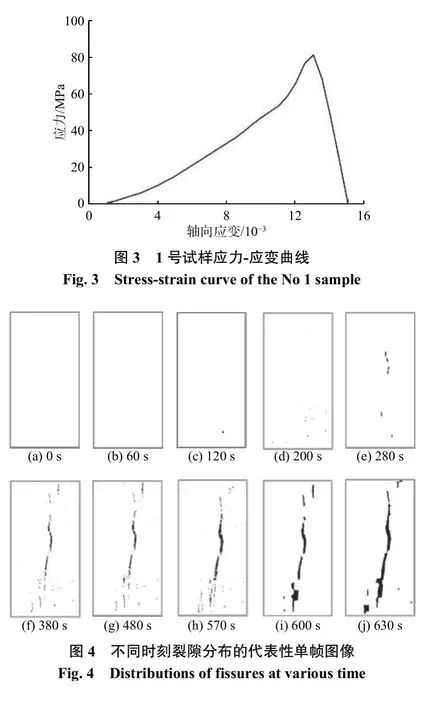
假设峰值应力为σmax、任一时刻的应力为σ,将应力水平定义为 α=σ/σmax,则不同应力水平下1号试样的外观图如图2所示,外荷作用下1号试样的应力-应变曲线如图3所示。

由图2可以看出,在加载初期,岩样没有发生明显变形。当应力水平为0.45时,岩样中部出现1条主裂隙,裂隙从试件中部向两端扩展,发生纵向破坏;当应力水平为0.65时,裂隙已经扩展到两端,且两端处出现多处细小裂缝;当应力水平为1.00时,裂缝贯穿两端,试样开始破坏。
根据应力-应变曲线(图3)和整个视频图像中裂隙的分布情况(图4),岩石变形破坏过程可以分成如下4个阶段:(1)岩石压密阶段(定义为阶段I)。此阶段既有裂隙逐渐闭合、没有新裂隙产生、分布时段是0~120 s;(2)弹性变形阶段(定义为阶段II)。此阶段既有裂隙已经闭合、没有新裂隙产生、分布时段是120~280 s;(3)裂隙扩展阶段(定义为阶段III)。此阶段出现新裂隙、既有裂隙重新张开并迅速扩展至上下两侧、分布时段是280~570 s;(4)整体破坏阶段(定义为阶段IV)。此阶段既有裂隙迅速相互连接贯通、分布时段是570~630 s。
将岩石变形破坏阶段分界时刻标注在应力-应变曲线中,得到标注不同变形破坏阶段的应力-应变曲线(图5)。根据分界时刻,得到不同变形破坏阶段岩石中不同组分的分布(图6)。为了方便对比,图6中还同时标出了不同时刻的裂隙分布情况。
由图5和图6可看出,在岩石不同变形破坏阶段,应力-应变曲线形态和不同组分分布具有不同的特征:
(1)阶段I:应力-应变曲线呈上凹形,没有新裂隙产生,各组分位移变化不明显,黑云母面积较小、呈分散点状分布,石英面积较大、呈小块状分布,长石面积最大、主要呈片状分布。
(2)阶段II:应力-应变曲线呈直线状态,裂隙首先出现在岩样中部、然后向上下两端扩展,黑云母的面积较小、无明显位移,石英中部向左右两侧移动,呈现为均匀的块状分布、相互之间连结紧密,长石主要以片状集中分布在左上角区域、以点状和块状分散分布在其他区域。
(3)阶段III:应力-应变曲线呈上凹形,裂隙宽度增大、从中部向岩样顶端延伸,黑云母向岩样上下两端缓慢移动,石英在岩样中间被压裂,其余石英向岩样两侧移动,长石在岩样中间被大量压裂,其余长石向两侧大幅移动。
(4)阶段IV:应力-应变曲线呈直线迅速下降,裂隙纵向贯穿于岩石表面直至岩样整体破坏,黑云母分散分布在岩样中部、位移持续增大,石英基本分布在裂隙两侧区域,长石面积明显减少,持续向裂隙两侧移动。
1.3 不同组分数字特征参数的计算
为便于后续分析,使用MATLAB编程和阈值分割法得到任意时刻t任意位置(x,y)处相应组分类型l的面积A(t,x,y,x,l),计算公式如下:
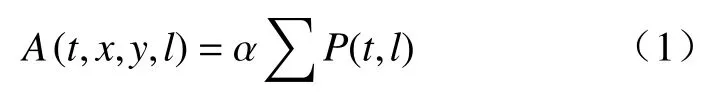
式中:l——组分类型,l=1、2、3、4分别为裂隙、黑云母、石英、长石;
P——与位置(x,y)处类型相同的像素点;
α−像素单位转换为物理单位的转换系数。
研究时,将A作为表征各细观组分的数字特征参数。
2 LSTM-NN模型的建立
2.1 LSTM-NN模型的结构

图6 花岗岩各阶段组分分布随时间的变化Fig.6 Composition distributions in various instants corresponding to different deformation and failure stages
长短期记忆神经网络(LSTM-NN)中有记忆细胞,由Hochreiter等[17]在1997年提出,可以选择性地对输入数据产生或长或短的记忆,是一种以循环神经网络(RNN)为基础改进的深度学习网络,对时序数据处理具有很好的效果,用于解决RNN出现的梯度爆炸和梯度弥散问题。
LSTM由输入层、隐藏层和输出层3部分组成,输出层结果不仅与当前输入有关、还与上一层的隐藏层有关、对时间序列产生了一定的记忆功能。LSTM-NN与普通RNN的主要区别在于算法中加入了判断信息是否有用的“处理器”,这个处理器作用的结构被称为细胞。在一个细胞中放置3扇门,分别叫输入门、遗忘门和输出门。信息进入到LSTM时根据设定的规则来判断是否有用:只有符合条件的信息才会留下,不符合的信息则进入遗忘门被遗忘,从而有效地解决数据中长期依赖的问题[18]。图7为LSTM结构图。
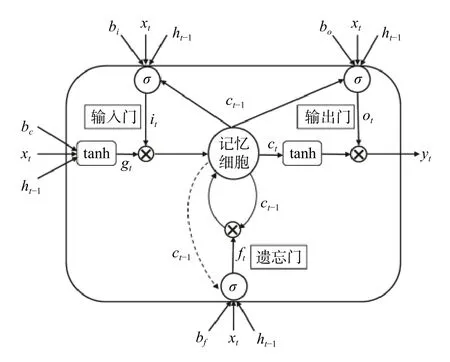
图7 LSTM储存单元基本架构图Fig.7 Structure of LSTM
LSTM中输入门it、遗忘门ft、输出门ot、输入结点gt、细胞状态ct和细胞输出yt按照式(2)~(7)计算:
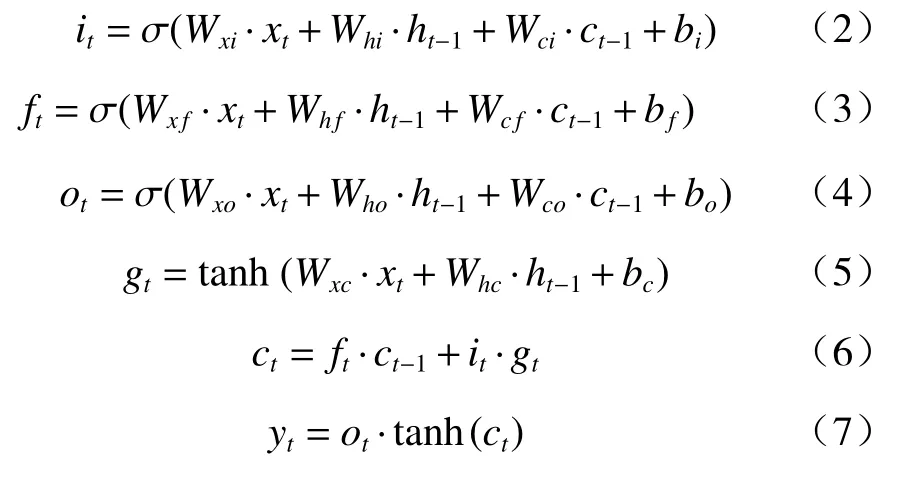
式中:xt∈Rk——输入的时间序列;
σ、tanh−Sigmoid和双曲线正切函数,σ作用于3个门上、表示对应信息的通过程度、输出为[0,1],0和1分别表示不允许和允许所有信息通过;
Wxi、Whi、Wci、Wxf、Whf、Wcf、Wxo、Who、Wco、Wxc、Whc——不同门对应的权重矩阵;
bi、bf、bo、bc−对应权重的偏置;·——矩阵对应元素相乘;
ht——时刻t及t之前存储所有有用信息的隐藏状态。
2.2 LSTM-NN模型的架构
本文建立的LSTM-NN的架构包含5层,分别是序列输入层、LSTM层、全连接层、分类概率层(softmax层)和分类输出层,如图8所示,该架构简要说明如下:
(1)序列输入层。将6个视频中不同组分数字特征参数(即A)时间序列作为初始数据,随机设定5个视频的阶段分类数据作为训练集,另1个视频的数据作为测试集。为避免存在异常和较多噪音数据、加快网络训练速度、提高模型训练精度,对初始数据进行标准化处理,并将标准化后的数据输入到LSTM-NN层。标准化计算公式为:

式中:xb——标准化后的数据;
x——初始数据;
µ、σ——初始数据的均值和方差。
(2)LSTM层。LSTM层由LSTM单元组成、结构见图7。该层用于对序列输入层数据进行长短记忆处理。
(3)全连接层。全连接层中每一个结点都与LSTM层的所有结点相连,用来把前边提取到的特征综合起来。
(4)分类概率层。分类概率层将全连接层所提取特征使用分类概率函数应用到输出层上。本文分类概率函数使用Sigmoid函数,计算公式为:
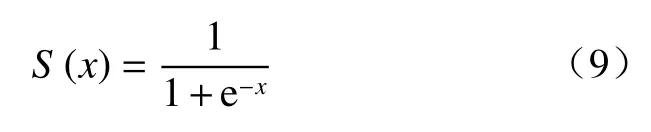
Sigmoid函数将全连接层的输出数据转换为[0,1]范围内的输出值,避免了数值爆炸现象,使数据在LSTMNN传递中聚拢。使用分类概率层得到不同变形破坏阶段的概率。
(5)分类输出层。分类输出层计算具有互斥类的、多分类问题的交叉熵损失。该层对输出数据进行分类、并与实际类别对比进行损失计算,通过网络的不断训练,输出最终判别结果、并得出分类准确率。

图8 基于LSTM-NN花岗岩的分类框架Fig.8 Granite classification framework based on LSTM-NN
2.3 LSTM-NN模型参数的确定
使用所建LSTM-NN模型对花岗岩变形破坏阶段进行分类时,需要对模型不断训练。训练参数主要有优化器、学习率和最大周期。
优化器:常用优化器有自适应梯度算法(Adaptive Gradient Algorithm,AdaGrad)[19]、均方根反向传播算法(Root Mean Square Prop,RMSProp)[20]和适应性动量估计算法(Adaptive Moment Estimation,Adam)[21]等。由于适应性动量估计算法是基于梯度随机优化的方法、占用资源较少、比其它随机优化方法表现更优[22],本文选用这一算法作为优化器。
学习率:学习率是最重要的超参数,通常在0.0和1.0之间,起到LSTM-NN训练时不断更新权重大小的作用。
最大周期:最大周期是使用所有样本完整训练的次数。随着最大周期的增加,数据传递次数增加,权重等参数更新次数也在增加。最大周期过大会导致网络出现过拟合现象。
2.4 LSTM-NN模型的评价指标
本文使用准确率P(i)和平均准确率A(i)作为LSTMNN模型的优劣评价指标,计算公式分别是:
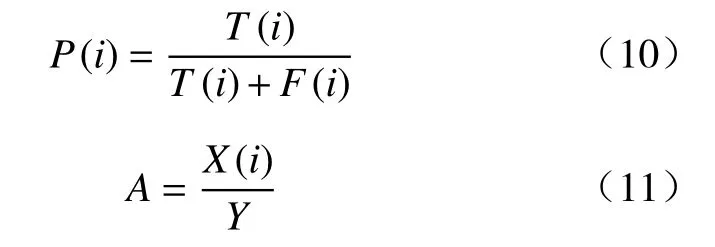
式中:T(i),F(i)——识别为第i阶段分类正确和分类错误的个数;
X(i)——识别分类正确阶段的个数;
Y——数据集含有的样本总数。
2.5 LSTM-NN模型参数的影响
下面以准确率作为评价指标,分析LSTM-NN模型主要参数(学习率和最大周期)对分类效果的影响。图9是不同组分在不同学习率和最大周期下的分类准确率。
由图9(a)可知,在学习率为0.005、最大周期为200时,裂隙阶段分类的准确率最高,为0.961 6;学习率为0.005的准确率高于学习率为0.001和0.010,说明学习率为0.010时模型出现过拟合,导致数据冗杂、准确率降低;裂隙阶段分类的准确率都在0.830 0以上,预测效果较好。
由图9(b)可知,黑云母各阶段分类在初始学习率为0.005、最大周期为200时准确率最高,为0.910 5;当学习率为0.001和最大周期大于250、学习率为0.005和最大周期大于200、学习率为0.010和最大周期大于200时模型出现过拟合。黑云母阶段分类的准确率基本在0.6800以上。
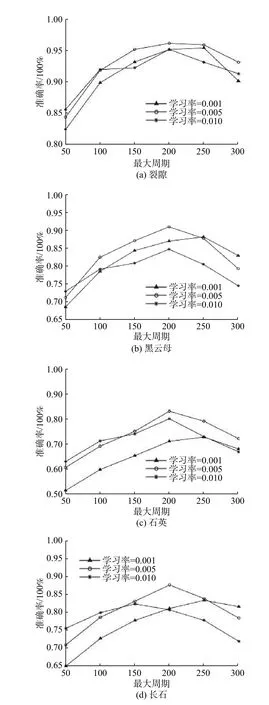
图9 不同组分在不同学习率和最大周期下的准确率Fig.9 Accuracies of various compositions at different learning rates and the maximum epoch
由图9(c)可知,石英各阶段分类在学习率为0.005、最大周期为200时准确率最高,为0.832 1;学习率在0.001和0.005的预测准确率明显高于学习率为0.01 0时的准确率。当学习率为0.001和0.005、最大周期为200处的准确率最高;当学习率为0.010、最大周期为250处的准确率最高;石英阶段分类的准确率基本为0.500 0~0.840 0,预测效果较差。
由图9(d)可知,长石各阶段分类在学习率为0.005、最大周期为200时准确率最高,为0.877 9;随着学习率和最大周期的变化,阶段分类的准确率为0.650 0~0.880 0。
综上所述,在学习率为0.005、最大周期为200时,裂隙、黑云母、石英和长石的阶段分类准确率最高,分别为0.961 6,0.910 5,0.832 1,0.877 9;不同成分阶段分类的准确率高低顺序为裂隙、黑云母、长石、石英,准确率都在0.800以上,预测效果较好;随着学习率和最大周期的变化,裂隙、黑云母、石英、长石的分类准确率分别为0.830 0~0.960 0、0.680 0~0.910 0、0.500 0~0.840 0、0.650 0~0.880 0。
3 基于LSTM-NN模型的阶段判别
3.1 不同变形破坏阶段的划分
以6个花岗岩单轴压缩试验的视频图像作为样本,根据前述变形破坏阶段的划分方法,得到6个基于试验视频的变形破坏阶段划分结果(表1)。
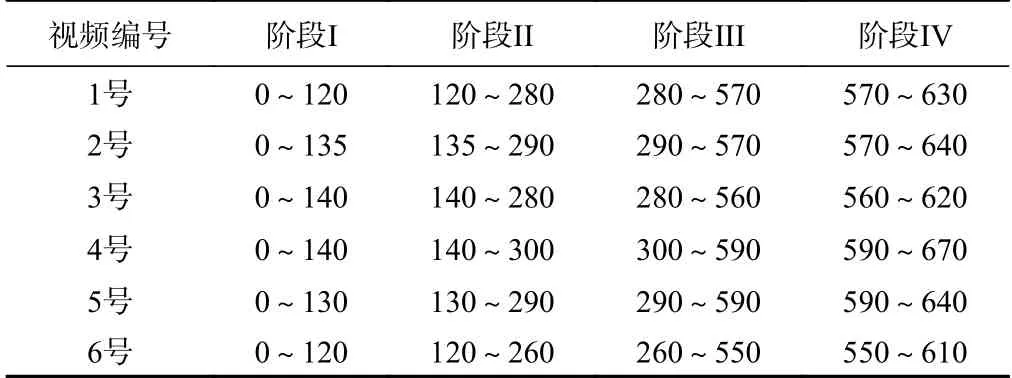
表1 6个试样不同变形破坏阶段的历时Table 1 Time interval of deformation and failure stages of 6 test videos /s
限于篇幅,下面以1号花岗岩为例(其他花岗岩变化情况类似),说明不同变形破坏阶段各组分面积的变化情况(图10)。
从图10(a)可以看出,阶段I和阶段II几乎没有裂隙产生,阶段III初期(280 s左右)裂隙面积迅速增长到1 287mm2,随后增长速度变缓;阶段IV裂隙面积继续增长,裂隙面积达到5 877mm2后花岗岩被整体破坏。
从图10(b)可以看出,阶段I和阶段II黑云母面积在9 400mm2左右,表现为动态稳定变化;阶段III黑云母面积有所增加,可能是裂隙的识别效果较差;阶段IV黑云母面积维持稳定。

图10 花岗岩各组分阶段分类Fig.10 Classification of granite compositions in stages
从图10(c)可以看出,阶段I和阶段II石英面积有所增长,阶段III初期石英面积从27 000mm2迅速下降到23 500mm2,随后面积涨幅不大,阶段IV石英面积增长到最初状态。
从图10(d)可以看出,长石面积缓慢下降,在阶段I长石面积最大,在阶段IV长石面积最小,在阶段II、III长石面积明显减少。
3.2 不同变形破坏阶段不同组分的判别准确率
不同变形破坏阶段不同组分准确率变化的柱状图见图11。从图11看出,在阶段I,判别准确率高低顺序是裂隙、黑云母、石英、长石;在阶段II,判别准确率高低顺序是黑云母(长石)、裂隙、石英,黑云母和长石的分类准确率达100%;在阶段III,不同组分判别效果最好,判别准确率高低顺序是石英、长石、裂隙、黑云母,石英分类准确率达100%;在阶段IV,判别准确率高低顺序是裂隙、黑云母、长石、石英,不同组分的分类判别效果最差,石英和长石判别准确率为0.400左右、判别效果较差。
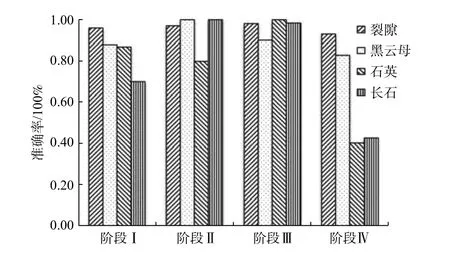
图11 不同阶段不同组分的判别准确率Fig.11 Accuracies of various compositions at different deformation and failure stages
3.3 整个变形破坏阶段的预测
采用前述所建LSTM-NN模型与相关改进参数(即采用Adam算法、学习率取0.005、最大周期取200),对岩石中不同成分数字参数(面积)进行阶段判别,不同组分在不同变形破坏阶段的判别准确率计算结果见表2。
由表2可以看出,使用所建LSTM-NN模型与不同组分数字特征参数,岩石变形破坏阶段整体判别的平均准确率为90.83%,可以实现岩石变形破坏阶段的快速判别。岩石不同组分中,裂隙在各成分中的判别效果最好,准确率为96.89%;黑云母、长石次之,准确率为88.17%~91.49%;石英最差,准确率为86.77%。
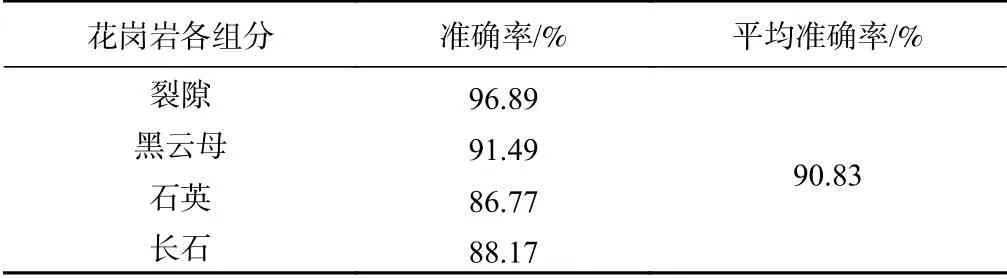
表2 各组分分类的准确率和平均准确率Table 2 Precision rate and average accuracy of eachcomposition classification
4 结论
(1)根据试验视频中裂隙发展情况,花岗岩单轴压缩条件下变形破坏过程可以分为岩石压密阶段(阶段I)、弹性变形阶段(阶段II)、裂隙扩展阶段(阶段III)和整体破坏阶段(阶段IV)。
(2)在LSTM-NN模型参数中,学习率和最大周期对变形破坏阶段准确率影响较大,二者分别取0.005和200时裂隙、黑云母、长石和石英阶段分类准确率最高、判别效果较好。
(3)对于不同变形破坏阶段来说,所建LSTMNN模型在阶段I时不同组分判别阶段的准确率高低顺序是裂隙、黑云母、石英、长石,在阶段II时相应的顺序是黑云母(长石)、裂隙、石英,在阶段III时的相应顺序是石英、长石、裂隙、黑云母,在阶段IV时的相应顺序是裂隙、黑云母、长石、石英,阶段III的判别效果最好,阶段IV的判别效果最差。
(4)对于岩石整个变形破坏过程来说,使用所建LSTM-NN模型与不同组分数字特征参数,变形破坏阶段整体判别的平均准确率为90.83%,判别准确率高低顺序是裂隙、黑云母、长石、石英。
