郑州市短历时强降水变化特征及重现期研究

2021-05-25朱业玉刘善峰

气象与环境科学 2021年2期

左璇，朱业玉，郭鹏，刘善峰

(1.中国气象局·河南省农业气象保障与应用技术重点开放实验室,郑州 450003; 2.河南省气候中心,郑州 450003; 3.中国气象局公共气象服务中心,北京 100081; 4.北京华新天力能源气象科技中心,北京100081; 5.国网河南省电力科学研究院,郑州 450000)

引言

现代城市是人口高度聚集、社会经济高度发达的地方，同时也是资源环境承载力矛盾最为突出的地方。近十年来随着我国城镇化的快速发展，2015年时全国城镇建设用地不足国土面积的1%，却承载了54%的人口，产出了84%的GDP[1]。快速城镇化建设过程中，由于城市开发的强度高、密度大，使用了大量硬质地面材料，改变了原有的自然生态状态和水文特性。因此，由短时强降水引发的城市内涝带来的一系列社会和经济问题，已成为困扰城市发展的主要气象灾害因素之一，这也暴露出城市在防御由短时强降水而导致的城市内涝方面的短板。我国诸多大中城市频繁发生严重的城市内涝灾害。2000年以来，平均每年发生200多起不同程度的城市内涝灾害，近七成城市发生过由短时强降水而引发的内涝。城市内涝问题越来越成为大众所关注的热点问题，同时也是众多海内外学者研究的焦点[2-5]。

近年来，随着中原经济区建设的快速推进，郑州主城区范围不断扩大，郑州内涝也呈现频发、多发的态势[6]。为预防城市内涝，首先需要了解致涝短时强降水的变化特征，以及不同历时的短时强降水重现期。国内有许多学者从不同角度对城市短历时强降水进行了分析和研究。贺芳芳等[7]运用SCS-CN模型对城市降雨径流过程进行模拟，对上海地区短历时强降水致灾阈值进行了推算。马京津等[8]根据北京市强降雨的时空变化特征进行分区，并进行了不同历时降雨量重现期的估算。唐传师等[9]通过分析江西省短历时降水的时空分布特征，对当地短历时降水与暴雨的关系进行了探讨。张启绍等[10]采用常规中尺度分析方法和Barnes滤波方法，对林州一次局地强降水过程的环流特征进行了分析。郭渠等[11]利用重庆地区逐分钟降水资料，对当地不同历时的短历时强降水空间分布特征进行了探讨并分区。王彬雁等[12]分析北京短历时强降水资料的变化特征，并利用概率分布函数进行拟合，应用多个概率密度函数对其重现期进行预估。郝莹等[13]根据安徽省49年小时降水资料，针对超过98%分位点的短历时强降水，进行了多角度的分析。杨新[14]利用西安逐日降水资料，分析了西安市降水量和降水频率的年、季变化特征，探讨了各等级降水的频率变化对总降水量变化的贡献。姚莉等[15]利用我国1991-2005年逐小时降水资料，通过概率分布、统计检验与极值分布等方法，研究了我国中东部地区逐时降水强度的时空分布特征及1 h最大雨强的50年、100年重现期估算等问题。目前对郑州市区域有关降水的研究，多侧重于强降水过程的预报预警特征分析[16-18]、降水日变化特征分析[19-22]、暴雨灾害区划或城市内涝模拟[23-29]等，且所使用的资料多在小时甚至日尺度之上，并对不同历时的降雨量进行区分。因此，本文基于郑州市气象观测站多年的短历时强降水资料，首先分析哪种短历时强降水对郑州影响较大，其次再分析代表短历时强降水的变化特征，最后分析哪种分布函数适宜于郑州短历时强降水分布拟合，对其进行概率检验和拟合，并最终给出不同历时强降水的重现期估算结果，以期能为城市规划、内涝防范和短历时强降水的预测预警气象服务等提供依据和参考。

1 资料与方法

1.1 资料

本文采用的短历时强降水数据来源于郑州市气象局观测站(以下简称为郑州气象站)。数据起止年代为1955至2018年，其中2005年以前的数据通过纸质记录信息化后再提取分析而得到，2005年以后的数据直接采用自动观测仪器分析得到。对于数据的选样则采用年最大值法[30]，逐年分别求出各降水历时的最大值，得到5、10、15、20、30、45、60、90、120、150、180、240、360、540、720、1440等共16个序列。

1.2 频率分析

强降水频率分析参照英国水文研究所出版的《Flood Estimation Handbook》中关于降水频率分析方法[31]，该方法依据年最大降水资料，采用降水指标变量和降水频率两个指标。其中降水指标变量为气象观测站点年最大降水量序列的中值，其计算首先把年最大降水量序列从小到大排序，若序列有n个数，n为奇数时，则选择第(n+1)/2个为中值，若n为偶数时，则中值是第n/2和(n/2)+1的平均数。因该指标不受降水资料序列中出现的异常偏大或偏小值的影响，所以该指标是一个比较稳定的统计变量。降水频率不同于以往的百分比概念，本文参考文献[31]所拟定的标准，定义其为单位时间内达到的降水总量值[32]。

1.3 极值分布模型选取及参数估计

本文拟采用指数分布、Gamma分布、Gumbel分布、PeasonⅢ分布、广义极值分布(GEV)等来具体分析哪种分布更适宜于郑州气象站短历时强降水拟合[33]。各种极值分布的拟合及检验效果，采用DPS(Data Processing System)数据处理系统中的“水文气象频率分析”模块来分析和处理，参数估计采用L矩估计或间隔最大积估计法[34]。

2 结果与分析

2.1 频率分析

依据降水指标变量，短历时强降水是指比较短时段之内的降水总量。从郑州气象站短历时强降水统计结果(表1)可以看出，在120 min以内的降水频率变化均是显著的，在120-360 min有可能会发生高达50 mm(暴雨级别)左右的降水过程，但在720 min以内降水量在100 mm(大暴雨级别)以上的概率比较小。

表1 郑州气象站各短历时强降水的统计特征

再从强降水频率的变化来看，45 min以内的降水频率下降幅度较大(大部分下降幅度大于0.2 mm/min)。此后，仅以0.10～0.16 mm/min的幅度下降，到180 min以后的降幅逐渐趋缓(下降幅度小于0.05 mm/min)。这说明180 min以内的降水强度变化较大，且180 min以上的降水渐趋稳定。所以，180 min以内是短历时强降水最具风险的时段。考虑到360 min以内的累计雨量较大，时间较短，也可构成一定的风险，因此本文以下部分的分析选取了360 min以内有代表性的5、60、180和360 min的短时强降水作为典型代表时段来作进一步分析。

2.2 演变趋势

从郑州气象站60多年来短时强降水各典型代表时段降水量的实际演变图来看(图1)，5 min年最大降水量(图1a)整体呈略增加趋势(通过0.05的显著性检验)，目前处于平均水平(9.2 mm)附近。1970s初中期、2000s中后期为降水量偏高时期。其中1973年和2007年为高值年，5 min降水量分别达到14.3和16.5 mm。60 min年最大降水量(图1b)整体呈不显著的增加趋势(未通过0.1的显著性检验)，但2000s中期到2013年左右下降趋势则更为明显(下降速率达到9.5 mm/a，通过0.01的显著性检验)，目前已处于平均水平(39.3 mm)以下。60 min强降水量高值也在1973年和2007年，60 min降水量分别达79.4和87.1 mm。

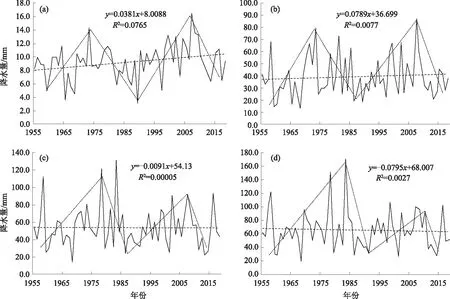
图1 1955-2018年郑州气象站不同短历时年最大降水量年际变化曲线

180 min年最大降水量(图1c)整体上没有显著的减少趋势(未通过0.1的显著性检验)，1960s初到1970s呈增加趋势，峰值出现在1970s后期。180 min强降水量高值在1955、1977和1982年，其最大降水量分别达113.2、120.7和130.4 mm。360 min年最大降水量(图1d)整体已经呈现不显著的减小趋势(未通过0.1的显著性检验)，且近30年来的平均最大降水量(61 mm)已经明显不如建站至1980s前期的30年均值(70 mm)。360 min强降水量高值在1978和1983年，其最大强降水量分别达151.1和170.8 mm。

综上分析，郑州60多年来各代表时段的短历时强降水均呈波动变化规律，大多呈现“M”型变化趋势，年际间差异较大。从各年代变化来看，1960s以前各时段降水量均呈现微弱减少趋势；从1960s初到1970s呈增加趋势；从1970s至1980s又呈现显著的下降趋势；从1980s后期至1990s呈明显减小的趋势，1990s到2000s中期，则又呈显著增加趋势；2000s中期到2013年左右又呈现下降趋势；最近几年略有增加。最大值主要集中在1970s中前期和2000s中后期，5 min和60 min强降水量以1980s后的最高，而180 min和360 min年强降水量则以1980s前的为高。

2.3 周期分析

为进一步分析各短历时强降水的演变规律，采用小波分析方法来分析其变化特征。在作小波变换时为滤掉序列自然周期的影响，对各短历时年最大降水量序列进行标准差标准化处理(中心化)[35]，以此变换后资料序列作为小波变换的输入资料。有关小波变换的原理及方法，国内已有很多的介绍及应用[36、37]，在此不再赘述。本文的计算方法和过程均参考文献[36]。

图2是代表短历时年最大降水量的小波变换结果，图中的符号反映振荡的位相，正负中心值反映了不同尺度振荡的振幅最大值，其中正值(实线)对应短历时强降水年最大降水量的偏多时期，而负值(虚线)对应着偏少时期。同样波幅中心所在的周期对应年最大降水量的偏多(少)期。

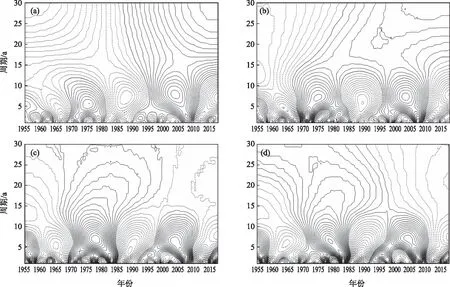
图2 郑州气象站不同短历时年最大降水量的小波变换

从图2可以看到，代表短历时年最大降水量的各种时间尺度周期变化在时间域中的分布有差异，1950年代中期以来，各个时期的主要振动周期是变化的。以5 min为例，最强的几个振动中心，分别在1960s中后期、1970s中期、1980s中后期、2000s中期及当前时段，其主周期大致为25 a、5～10 a，即图2(a)中几个正等值线中心对应的周期。当前郑州正处于30 a周期显著时期内；1960s中前期、1970s中期及2000s中期郑州处于5～10 a周期内。60 min与5 min的变化周期较为一致。180 min和360 min的与5 min和60 min的5～10 a的周期变化基本一致。由此可见，不同尺度周期信号的强弱在时—频域中的分布具有较强的局部特征，这可能与影响郑州区域的气候系统内在变化有关，有待进一步分析与揭示。

2.4 极值分布检验及重现期估算

2.4.1 极值分布检验

城市防灾减灾中，不仅需要了解短历时强降水的演变规律，同时还需了解不同短历时强降水的不同重现期的降水量，这对于灾害风险区划、评估、预警及防治等均有参考作用。

以往很多研究均表明[38-40]，降水概率分布多呈现偏态分布，可用Γ分布来拟合其分布形态，而短历时强降水的分布更具有偏斜特征，历时越短其离散程度也更大。在降水极值分布模拟分析中，经常采用指数分布、Gamma分布、Gumbel分布、PeasonⅢ分布、广义极值分布(GEV)等方法来拟合降水的极值概率分布型，但到底哪种方法模拟精度最高，需通过检验指标来具体判断。

本文选用指数分布、Gamma分布、Gumbel分布、PeasonⅢ分布、广义极值分布等5种分布函数对代表短历时降水进行检验，其结果如表2。

表2 郑州气象站5、60、180、360 min短历时强降水各分布型检验结果

如表2所示，半数分布类型用L矩估计方法拟合结果较好，另一部分用间隔最大积估计方法的拟合结果较好。在5 min历时降水中，PeasonⅢ分布拟合结果最优，但相对残差均方值仍超过5%，指数分布不成立；60 min最大降水量拟合结果中，广义极值分布拟合结果最优，且拟合精度高，相对残差均方值小于5%；180 min降水拟合结果中，Gumbel分布拟合结果最优，且拟合精度高，相对残差均方值小于5%；360 min最大降水量拟合中，广义极值分布拟合结果最优，且相对残差均方值小于5%，拟合精度高。

从以上分析结果可见，PeasonⅢ和GEV对郑州短历时强降水的拟合较好。通过K-S检验发现，对不同重现期下不同短历时强降水的估算结果均可信。GEV的K-S检验结果均小于其他分布的检验结果，说明GEV分布对郑州短历时强降水的拟合效果要好于其他概率函数分布拟合效果。下文采用GEV方法来估算郑州不同短历时强降水的重现期。

2.4.2 广义极值分布拟合

由Q-Q图(图3)可见，5、60、180、360 min短历时降水模型拟合效果均较好。从Q-Q图的拟合效果来看，在尾部模型模拟的结果与观测值有一定误差，且随着历时长度的增加，模拟值和观测值偏差有所增加。但总体来说，郑州气象站各代表历时的降水极值基本符合GEV分布。

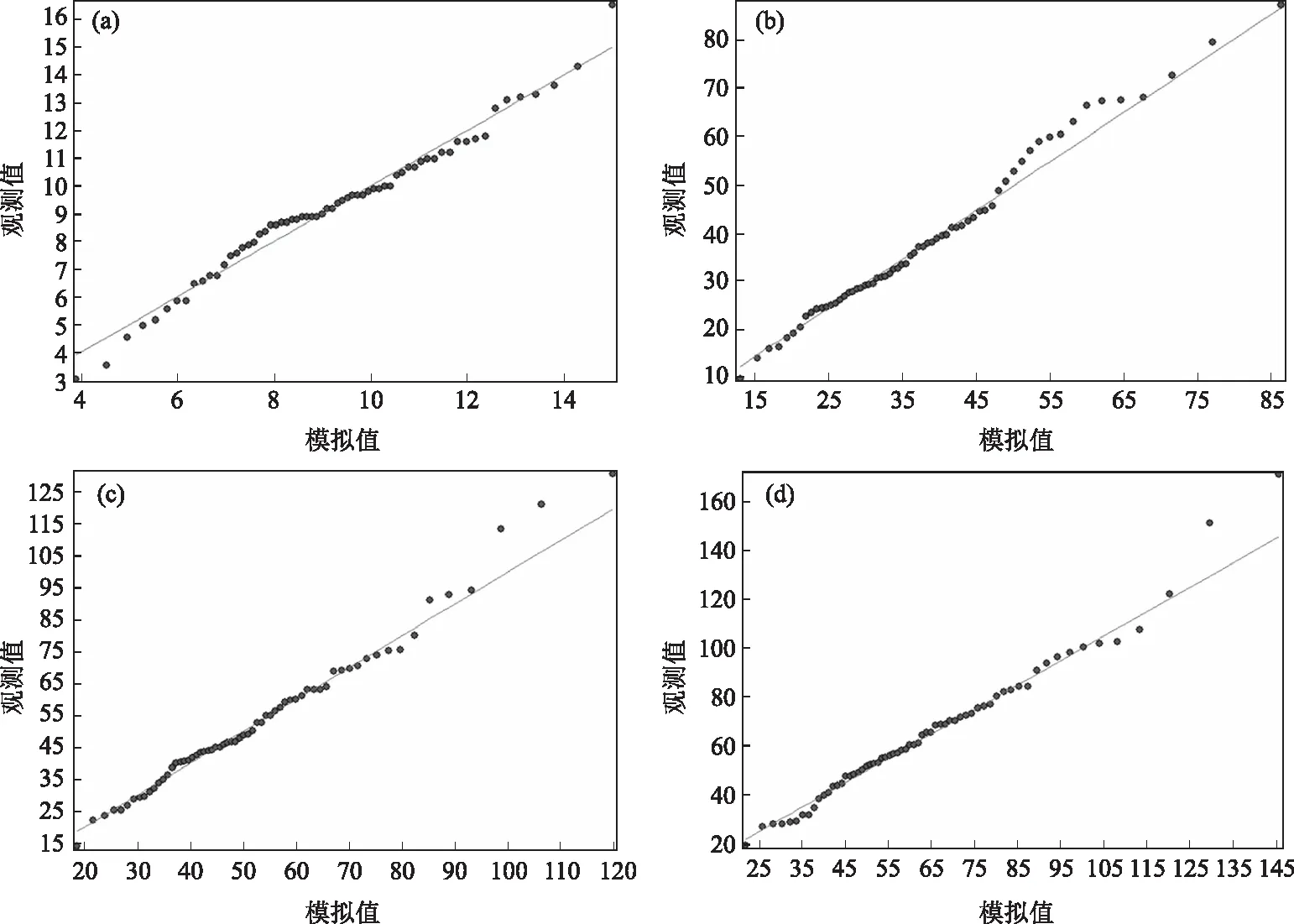
图3 利用GEV模拟郑州气象站不同短历时强降水的Q-Q图

图4为郑州气象站5、60、180、360 min短历时降水P-P分布图。从P-P图中可见，各历时降水也基本符合GEV分布，概率散点图中模型和观测值组成的序列基本都位于直线上，其重现期水平的检验结果也表明均处于置信区间内。

图4 利用GEV模拟郑州气象站不同短时强降水的P-P图

2.4.3 重现期估算

应用广义极值分布(GEV)方法，对郑州气象站不同历时短时强降水序列进行重现期估算，估算结果如表3。

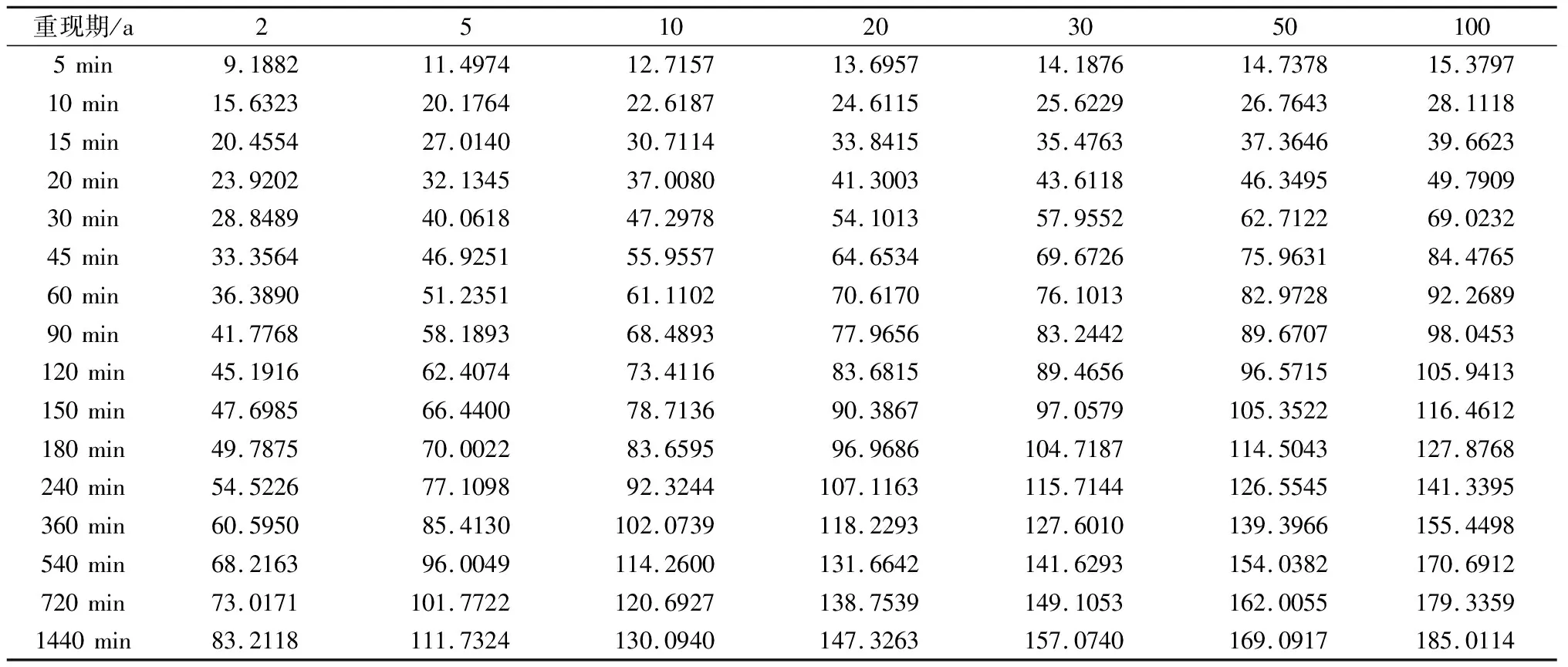
表3 郑州气象站各历时短时强降水重现期估算结果 mm

从郑州气象站不同历时强降水重现期的估算结果来看，5 min降水量各重现期估算结果在9.1～15.4 mm。对比实测资料，1954-2018年5 min最大降水量出现在2007年8月2日09:40-09:44，时段降水量高达16.5 mm，其超过百年一遇水平。60 min降水量各重现期估算结果在36.3～92.3 mm。对比实测资料，1954-2018年60 min最大降水量出现在2007年8月2日09:10-10:09，时段降水量高达87.1 mm，也超过了五十年一遇水平，接近百年一遇水平。180 min降水量各重现期估算结果在49.7～127.9 mm。对比实测资料，1954-2018年180 min最大降水量出现在1978年7月2日00:03-03:02，时段降水量为120.7 mm，超过了五十年一遇水平，也接近百年一遇水平。360 min降水量各重现期估算结果在60.5～155.5 mm。对比实测资料，1954-2018年360 min最大降水量出现在1983年8月9日07:35-13:34，时段降水量高达170.8 mm，超过了百年一遇水平。

上述不同历时短时强降水的重现期估算结果与气象站实测资料的对比结果表明，不同历时短时强降水值均超过了五十年一遇水平，有些超过了百年一遇水平。因此，极值分析结果较为可靠。