弯管内天然气水合物颗粒螺旋流动特性数值模拟
2021-05-25李立军赵书华丁博洋饶永超王树立
李立军,赵书华,丁博洋,饶永超,王树立
(常州大学 石油工程学院,江苏 常州 213000)
管道输送是天然气输送的主要形式之一。 冬季的油田地面或海底管道输送,由于低温高压环境,很容易导致天然气水合物的形成[1]。 天然气水合物由氢键形成的水分子空腔内包含小气体分子而稳定存在,可导致管道堵塞问题发生,造成严重的安全隐患[2]。 防治水合物堵塞的方法主要有降压法、脱水法、隔热法及添加化学抑制剂法等[3],例如在海上油田,避免水合物形成的首选方法是连续注入热力学抑制剂。传统的水合物 防治方法主要是通过破坏水合物生成所需要的温度和压力等相平衡条件来达到抑制水合物生成的目的,普遍存在成本高、污染大等不足[4]。 近年来,允许管道内生成一定量的天然气水合物颗粒,但可保证水合物浆液安全流动的冷流技术引起行业内普遍关注,该技术为防止水合物堵塞管道提供了新的途径[5,6]。
管道螺旋流动是一种通过在管道中安装起旋装置改变管道流动边界,从而改变流动方向,使管道内的流体具有轴向速度和切向速度的流动形式[7]。 应用螺旋流来进行天然气的管道输送,其轴向速度可以保证流体的连续输送,切向速度可以增大流体与管壁之间的剪切力,使水合物颗粒不易在管壁处发生沉积黏结,同等条件下增大了对水合物的输送能力,从而可以扩大含水合物的天然气管道的安全输送范围[8]。 Horii[9]以空气为介质,研究了螺旋流流动特性及机理。 孙西欢等[10]以局部螺旋流发生器为研究对象进行了切向流速和轴向流速的分布规律研究,发现切向流速在管道截面为线性分布,轴向流速呈类对数分布。 王树立等[11-15]在气液两相流流型方面也进行了探索,研究了以叶轮及扭带起旋的气液两相螺旋流的流型及流型转换边界,并发明了一种新的管道螺旋流气体水合物输送方法,为提高天然气运输的安全性和经济性、避免管道堵塞提供了新的途径。
目前对输气管道螺旋颗粒流动的研究多以直管为主,而关于含有弯管段的水合物颗粒流动的研究相对较少。 为此,本文利用数值模拟方法对螺旋流携水合物颗粒在弯管中的速度分布、 涡流衰减、颗粒沉积等规律进行了研究。
1 模型建立
1.1 物理模型
物理模型采用一条内径为25 mm,长度为2.5 m的管道,其中管道前段和尾端分别为1 m长的直管,中间段为长度是0.5 m的90°弯管,管道水平放置,如图1所示。管道入口段装有短扭带起旋器。起旋扭带长为0.5 m,采用3个扭率(扭带每扭转360°的长度H与扭带宽度D之比),分别为6.2、7.4和8.8。 采用结构网格方式对扭带进行网格划分,如图2所示。 对含有起旋器的管道段进行了网格加密处理。 考虑初始化的时间、计算量、数值耗散等原因,经网格无关性检验后,选取网格单元数约为80 万个。 计算模型三维坐标系的坐标原点位于管道的入口界面圆心处,沿Z轴方向为流入方向,沿Y轴方向为出口方向,X轴的负方向为重力方向。

图1 管道几何模型

图2 扭带网格
1.2 数学模型
模型在建立时,考虑了重力带来的影响,并将流体视为不可压缩流体;颗粒在接触到固定且恒温的壁面后,经过反弹作用后继续前进,与壁面碰撞的过程中,不变形破碎;将问题简化为三维、非稳态、常物性的气固两相流动。
连续性方程:

式中,ρ为密度,kg/m3;t为时间,s。
动量方程:

式中,p为静压,Pa;为粘性应力张量。
离散相模型的计算主要包括连续相和分散相两个部分组成。 DPM模型通过计算颗粒受到的作用力得到颗粒的运动方程,DPM模型的颗粒运动方程对时间的积分可以得到颗粒运动轨迹。 在z方向固体颗粒轨迹的运动方程为:

式中,up为颗粒速度,m/s;gz为重力加速度在z方向上的分量,m/s2;ρp为颗粒密度,kg/m3。
其中颗粒受到其他作用力Fz主要包括颗粒周围流体加速而引起的附加质量力、布朗力、萨夫曼升力等。 附加质量力主要作用于流体相密度大于颗粒密度的情况下,而管道内水合物颗粒密度是大于气流密度的,故不需要考虑附加质量力。
1.3 计算方法与边界条件
计算中选取的是离散相模型,并采用压力基、隐式求解器对天然气管道进行气固两相三维螺旋流的瞬态模拟。模拟计算中的湍流模型采用RNGk-ε模型,k-ε模型通过引入湍动黏度将湍流应力表示成湍动黏度的函数,RNGk-ε模型是在k-ε模型的基础上在ε方程中添加了附加项, 提高了旋转流动计算的准确性。 颗粒运动描述采用DPM模型,通过参数设置可以改变射入粒子的物性参数、速度以及质量流量等。 动量分量、湍动能分量和耗散率均采用具有二阶精度的二阶迎风插值格式。 压力和速度耦合采用SIMPLEC算法,压力采用多维线性重建方法重建表面压力的二阶格式。
进口边界采用速度进口条件。气相为天然气,密度为0.77 kg/m3。 固相为水合物颗粒,密度为650 kg/m3,颗粒粒径为0.06 mm,入口水合物颗粒质量流量为10-6kg/s。 天然气流速选取3 m/s、6 m/s和13 m/s。 流动为等温绝热,出口边界采用压力出口。 管壁条件采用无滑移的固定壁面,考虑重力影响。
2 计算结果与分析
2.1 模型验证
为了验证模型的可靠性,自行搭建了一条长为1.2 m, 管道内径为25 mm的管道, 用颗粒粒径为0.06 mm的颗粒代替水合物颗粒在管道中随气体流动,实验在常温常压下进行。 将实验结果与模拟结果进行对比,对比结果如图3所示。 由图3可看出,在实验与模拟工况的雷诺数范围内, 结果误差较小,因此可以将该模型用于含有水合物颗粒的天然气输送模拟。

图3 压降随雷诺数变化曲线
2.2 气相速度分布
图4为扭带扭率为6.2、流动雷诺数Re= 20000时,管道不同截面位置的速度分布图。 从图4中可以看出,由于扭带的作用,在起旋段截面处的速度被分割成两个区域,区域内的速度极大值呈中心对称分布,集中在区域一侧。 由于扭带的作用,流体在此区间内高速地、螺旋状地向前流动。 而从图中的速度矢量变化可以看出,随着流动距离的增加,螺旋流的涡流强度逐渐减弱,使得速度极大值的区域逐渐向管道中心处融合成为一个区域。 当流体进入弯管后,由于所产生的离心力,速度最大值区域向管道外侧偏移。 从与弯管入口截面夹角α为30°位置(α30°)的速度分布图可以看出,速度极大值区域位于弯道的下外侧,而不是正外侧,说明螺旋流动的效果能够到达此处,这保证了水合物颗粒能够随流体顺利通过弯管,使颗粒不在管壁处发生沉积。 流体流出弯管后,沿尾段直管继续流动,螺旋流效果以及弯管带来的离心作用逐渐衰弱,速度极大值区域恢复到管道中心。
为了更好地了解速度的变化情况, 图5为不同截面中心线上的速度分布曲线。 从图5中可以看出,在起旋段(距入口25~500 mm),截面中心线上的速度分布呈“m”形的双峰结构。 这是因为近壁面及扭带两侧,处于粘性底层的区域压力梯度较大,而螺旋流导致的速度最大值区域分布于中心两侧。 而随着流动距离的增加,螺旋流动逐渐衰弱,速度分布曲线变为具有三个不明显峰的结构。 而在弯管中,由于离心力的作用,流体向管道外侧挤压,在螺旋流的共同作用下,速度发生偏移。 随着流体的继续流动,螺旋流作用消失,导致曲线不再出现明显峰值,呈稳定的“n”形结构。
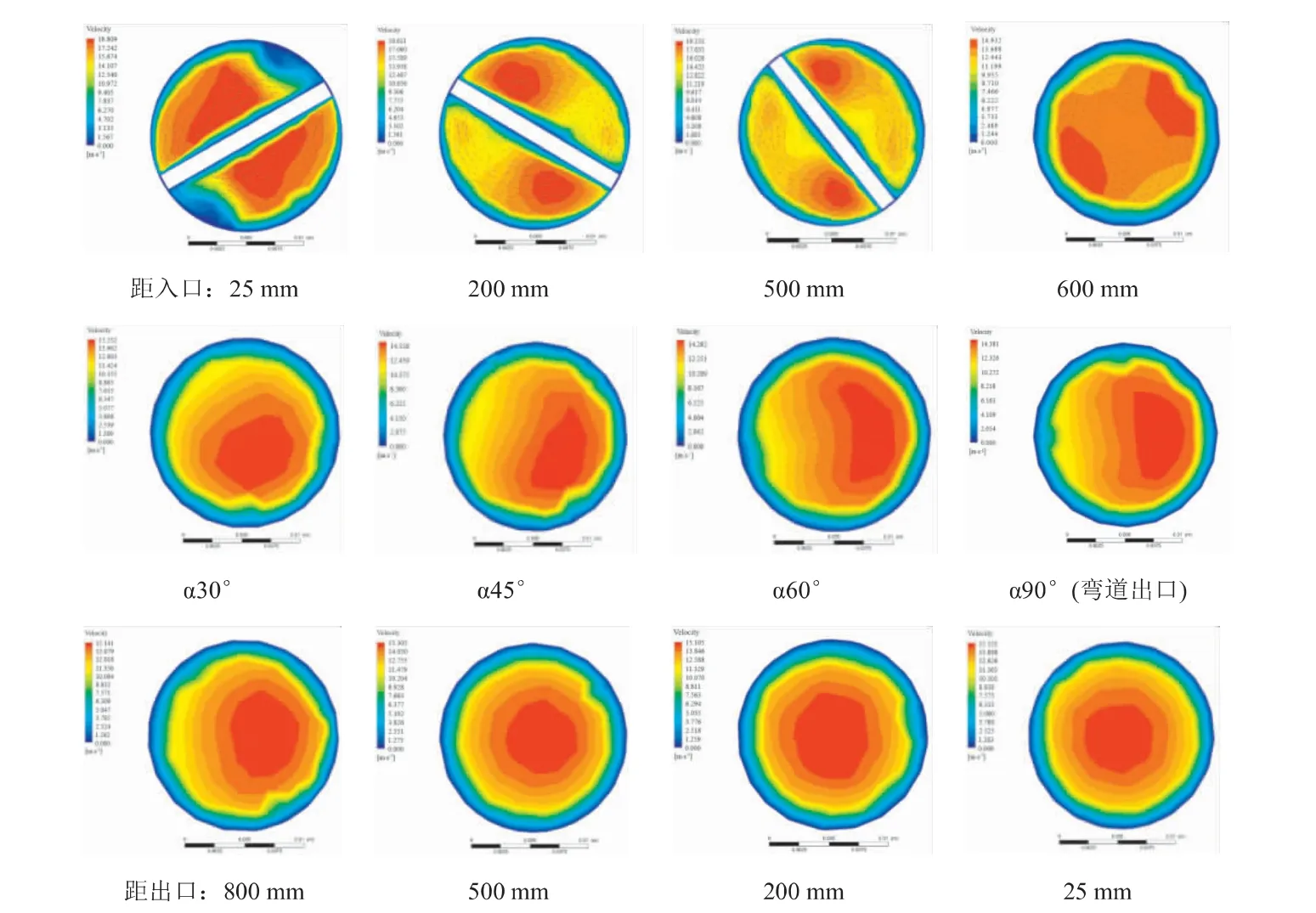
图4 管道不同截面速度分布

图5 管道不同截面中心线上的速度分布
2.3 湍流强度分布
湍流强度简称湍流度或湍强,是衡量湍流强弱的相对指标, 其强度越大则流体相间的掺混越均匀。 对于均匀各向同性的湍流,湍流强度Tu可以定义为:

图6为管道不同位置截面中心线上的湍流强度分布。 图6(a)所示为管道前段(弯管前直管段)的不同位置截面中心线上的湍流强度分布,其中扭带起旋段(距入口25~500 mm),曲线呈“w”形倒双峰结构,管壁和扭带中心处的湍流强度较大,中心两侧较低。 由于脉动速度在壁面处为零,在距离壁面很近的区域内迅速增加并达到最大值, 然后再下降,所以在扭带起旋段的截面上, 经过管道壁面—扭带—管道壁面,脉动速度的均方根值先迅速达到峰值再下降达到谷值,后上升达到新峰值再下降到谷值,后上升并达到峰值。 而在脱离扭带后(600~1000 mm),由于没有扭带的扰动,脉动速度仅在两侧壁面达到峰值,在管道中心处达到谷值,导致湍流强度的分布曲线逐渐变为“v”形。 在图6(b)所示的管道弯管段,由于流体受到离心力及螺旋流的作用,导致谷值有一定的偏移,但不影响曲线的整体形态。刚进入弯管段时谷值较低,进入弯管后,离心力的作用带来的二次流在一定程度上增大了湍流强度,但随着流动距离的增加,螺旋流逐渐衰减,湍流强度逐渐降低。尾段直管段的湍流强度分布与弯管中的曲线形状相似,由于弯管的离心力作用逐渐衰弱,距出口越近,曲线的偏移程度越低,如图6(c)所示。

图6 管道不同截面中心线上的湍流强度分布
2.4 水合物颗粒质量浓度分布
图7为不同时间点弯道各截面颗粒位置及质量浓度分布情况。 由图7可以看出,在高流速以及强螺旋流的作用下,当流体携带颗粒进入弯管时,质量浓度的极大值区域分布在近壁面处,管道中心的浓度较低。 这是因为螺旋流动是一种具有切向速度与轴向速度的运动,其切向速度使得颗粒在流体的携带下高度旋转,被均匀地分散开来,而轴向速度保证了流体能够持续地向前流动。 这种旋浮特性,使其对固体颗粒有更强的携带能力,不易沉积。 当颗粒流入弯管后,由于螺旋流、弯管离心力的作用,颗粒以较高的速度集中在管道上外侧,并伴随着流体持续向前运动。 随着流动距离的增加螺旋流逐渐衰减,颗粒在流出弯道后,由于重力的作用集中在管道中下处,在高流速的作用下,随流体最终流出管道,如图8所示。
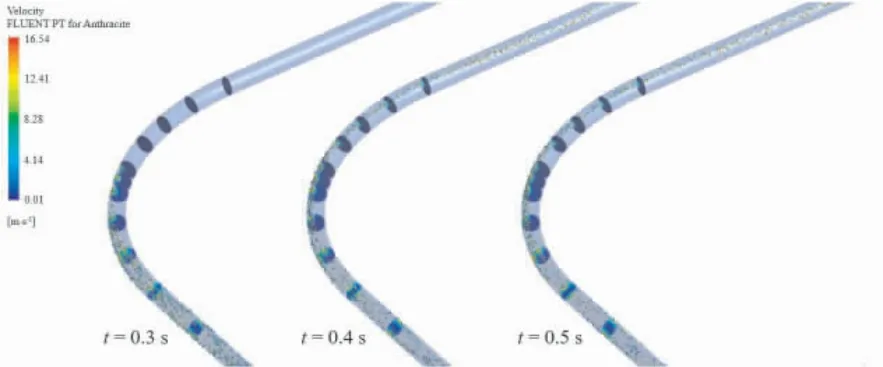
图7 不同时间弯管各截面颗粒质量浓度分布

图8 出口处颗粒质量浓度分布
图9为不同扭率下弯管不同位置截面中心线上的颗粒质量浓度分布情况。 由于受到重力和离心力的作用,颗粒随流体被挤压在管壁上,导致了部分动能的损失,在中低流速下,颗粒较难被拾起,就会发生沉积。 在螺旋流动效果下,颗粒在流入弯道前被均匀地分散在近壁面处,中心位置的质量浓度较低,呈“(”形结构分布,而且扭率越小,螺旋流动的效果越明显。 随着流动距离的增加,螺旋流对颗粒产生的切向力在重力和离心力的作用下逐渐减弱,螺旋流动的效果逐渐衰弱, 颗粒开始向中心处聚集,分散效果逐渐消失。 扭带的扭率越小,当颗粒流出弯管时,中心颗粒浓度越低,表明大量颗粒随着流体流出弯管。 由此可见,扭带的加入可以防止颗粒沉积在管壁上,提高了流体对颗粒的输送能力,有利于输送管道的安全运行。
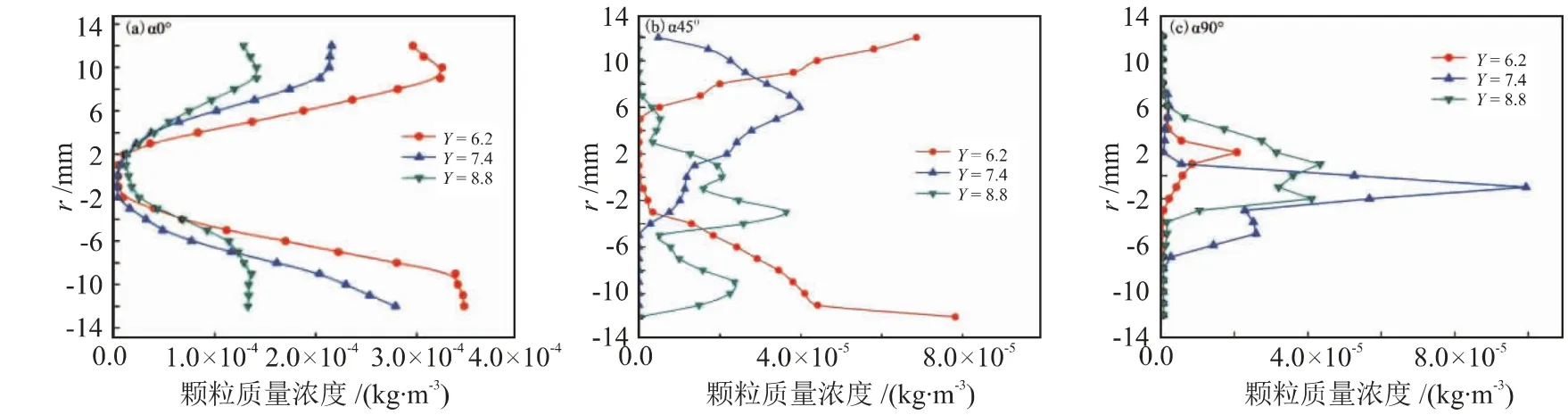
图9 不同扭率下弯管不同位置颗粒质量浓度分布
3 结论
(1)由于扭带的作用,起旋段的速度分布被分割为两个区域,各自区域内形成速度极大值。 随着流动距离的增加,螺旋流逐渐衰弱,速度极大值的区域逐渐向管道中心处融合成为一个区域,在尾段重新回归中心。
(2)在弯管内,由于螺旋流与离心力的共同作用,流体速度极大值区域发生偏移,说明螺旋流动的效果能够维持一个较长的距离。
(3)扭带起旋段,湍流强度分布呈“w”形倒双峰结构,无扭带处呈“v”形结构。 进入弯管后,离心力的作用带来的二次流及螺旋流的影响在一定程度上增大了湍流强度并导致了偏移,增大了流体相间的掺混程度,使颗粒不易沉积在管壁上。
(4)水合物颗粒在进入弯道前,受螺旋流的影响已经被均匀地分散在近壁面处。 在螺旋流的切向力作用下,相比无扭带的光管,流体对颗粒有着更强的携带能力,且扭率越小,螺旋流动的效果越明显,颗粒越不易沉积在管壁上,利于安全输送。
