一种新的土壤冻融特征曲线模型
2021-05-24付子腾吴青柏MilesDYCK何海龙
付子腾, 吴青柏, Miles DYCK, 何海龙
(1.西北农林科技大学资源环境学院,陕西 杨凌 712100; 2.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,甘肃 兰州 730000; 3.Department of Renewable Resources,University of Alberta,AB,T6G 2H1,Canada)
0 引言
冻土是指温度保持在或低于水的冰点,并含有冰的岩石和土壤,分为短时冻土(冻结时间数小时至半月)、季节冻土(冻结时间在半月至数月)和多年冻土(冻结时间在两年以上)[1]。在冻土中,冰和液态水(未冻水)共存,其含量随冻融过程中温度的变化而变化。未冻水含量和含冰量的变化显著影响冻土的物理和机械性能,从而决定寒区工程建设(如:房屋、道路、石油管线等)的成败[2-3]。同时,冻融循环过程也会带来如土壤冻融侵蚀、洪水、污染物的迁移、地下水上升引起的土壤盐渍化等一系列环境问题[4-7]。因此,掌握冻融过程中土壤水热耦合的变化机理对生产生活有至关重要的作用。
通常,纯水的冻结发生在某一确定的温度下[8],具有确定的凝固点,但在湿润的土壤中,即使当温度低于自由水的冰点时,土壤中所含水分也不会立刻转化为固态,而是随着温度的降低表现出相对平滑的转变,以曲线的形式降低[9-12]。由于土颗粒表面能的作用,土体中始终会保持一定数量的液态水被称作未冻水[1],当温度继续降低,更多的未冻水会转化成冰,此时毛管力和吸附力会被放大,剩余的未冻水会以薄膜水的形式存在[13]。当温度低于一定值时,随着温度的进一步降低,未冻水含量保持不变,该温度下的未冻水含量被称为残余水含量θres[14-16]。冻融过程中未冻水含量θl随温度T(℃)的变化曲线被定义为土壤冻融特征曲线(SFTC),代表了冻土中液态水含量和能量状态之间的关系[17],其中未冻水含量θl是指土壤孔隙中没有冻结的那部分含水量(用体积含水量表示,单位为cm3·cm-3)。一般来说,决定冻土中未冻水含量大小的主要因素是温度,其次是孔隙水压力和土质(包括土颗粒的矿物化学成分、分散度、含水量、密度、水溶液的成分和浓度等)[18]。温度作为主要影响因子,直接决定冻土中未冻水含量的高低,其他因素虽不是主要影响因子,但也显著影响着冻融特征曲线的变化。在一定的温度范围内,未冻水含量随孔隙水压力和溶质浓度的增大而增大;相同条件下溶质浓度越大的土壤残余水含量也越高,此外,土体液态水中溶质的存在还会引起水分凝固点的降低[9],从而影响土壤冻融特征曲线。土壤的质地和结构包括比表面积、矿物组分、土壤颗粒级配等,这些性质会影响毛管力和吸附力的大小,进而决定冻土中未冻水含量及残余水含量[19]。
有关冻融特征曲线数学表达的研究已有很多,许多学者也各自通过实验数据和理论推导建立了相关的模型[15,20-34]。这些模型一般包括两类:一类是基于土壤基本物理性质提出的半经验公式[14-15,23],一类则是通过类比水分特征曲线而提出计算未冻水含量的公式[7,22,24-25]。这些模型虽然在各自文章中能较好地拟合实验数据,但在实际应用中仍然有其局限性:(1)很多模型只适用于饱和砂土,而且忽视了溶质浓度所引起的凝固点降低现象[14-15];(2)认为未冻水含量的变化只依赖于温度和土壤属性,忽视了土壤中初始含水量的影响[34],而Tice和Anderson[35]的研究表明,在给定的温度下,土壤未冻水含量会随着土壤初始含水量的增加而增加;(3)部分模型形式复杂,参数繁多且只能应用于某种单一的土壤中,如果推广到其他土壤中,则预测结果偏离实际值[36]。
本文回顾了现有的冻融特征曲线模型,基于水分特征曲线与冻融特征曲线的相似性和平行关系,提出一种新的冻融特征曲线表达式。新模型与van Genuchten[37]水分特征曲线(SWCC)相似,考虑到了初始含水量对未冻水含量的影响,包含两个参数α、β,其中参数α和土壤自身的物理性质有关,参数β则受初始含水量的影响。此外,本文还根据已有数据对模型作了修正,考虑到溶质浓度对未冻水含量的影响,加入参数Tf,使其能适用于不同溶质浓度的土壤中。下面将对模型的确立过程、参数拟合、以及模型的验证作详细的说明,同时作模型参数的敏感性分析,以研究模型参数α和β的具体物理意义。
1 模型回顾
冻融特征曲线既能为研究土壤冻融过程和高寒地区水文模型提供理论支持,同时也是进行寒区工程设计及施工建设的理论基础,能否精确模拟某种土壤中的水热耦合运移对于寒区生产建设至关重要。许多学者已基于土壤的各种基本参数建立了相关的经验模型,包括线性、分段、指数和幂函数模型等[36,38]。但由于早期对于冻结过程中恰当的数学表示形式存在分歧,到现在仍未解决,以至于回顾这些模型和经验公式时,现有模型结构之间由于适用条件和范围的不同而表现出非常明显的差异。
1.1 Anderson and Tice(1972)模型
土壤物理特性(如土壤干密度、土壤颗粒大小、土壤孔隙度、比表面积等)都会影响冻土中未冻水含量,进而影响土壤冻融特征曲线的变化[37]。因此,根据土壤的物理特性,尤其是比表面积,可以建立一个简单的模型来预测土壤中未冻水含量[28]:
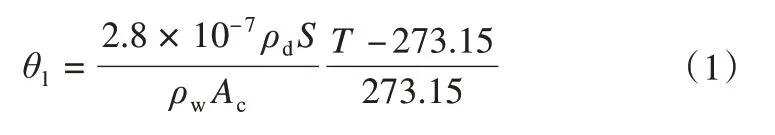
式中:θl为体积未冻水含量(cm3·cm-3);ρd和ρw分别为土壤干密度和标准状态下未冻水的密度(g·cm-3);S为土壤比表面积(m2·g-1);Ac为塑性指数与土壤颗粒小于2 μm 含量所占百分数的比值;T表示温度,本文中全部使用摄氏温度(℃)来表示。
Anderson[20,39]通过等温量热计和单位表面积归一化来确定土壤未冻水含量,根据实际测定的未冻水含量数据总结了不同含水量与比表面积之间的关系,提出了一种更为简单的幂函数模型:

式中:a和b为土壤特征参数与土壤比表面积有关。Kozlowski[14]给出了参数和土壤表面积之间的关系:
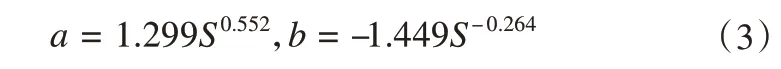
该式成立的隐含条件是假定在无穷低的温度下残余水含量为零[40]。联立式(2)和(3):

式(4)表明,只需测定土壤比表面积和干密度即可描述未冻水含量随温度的变化特征。因此,尽管幂函数模型提出已有几十年历史,但由于其形式简单便于应用,各种文献及资料中仍普遍采用该方法来估算冻土中的未冻水含量[1]。
1.2 Mckenzie(2007)模型
Mckenzie 等[15]提出了一个线性分段函数来近似地描述土壤冻融特征曲线:

式中:m为线性参数,Tres为未冻水含量减少到残余水含量的温度,假定为-12 ℃[15]。此外,Mckenzie等[15]还给出了另一个指数函数来预测未冻水含量:
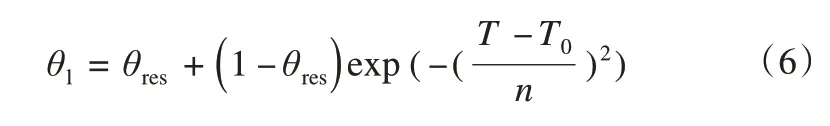
式中:n为拟合参数;T0为标准状态下自由水的冰点。相比式(5)、式(6)对未冻水含量与温度之间关系的描述更符合实际的实验结果[15]。
1.3 Kozlowski(2007)和Zhang(2008)模型
Kozlowski[14]对6 种 黏 土 进 行 差 示 扫 描 量 热 法实验后提出了土壤冻融特征曲线的半经验模型,该模型由三部分组成:

式中:wl、wtotal、wres分别为用重量含水量表示的未冻水含量、土壤总含水量和残余水含量;Tf代表凝固点的降低量。用体积含水量替换重量含水量则式(7)可变形为:

在这里Kozlowski 通过土壤塑限和含水总量来计算Tf:
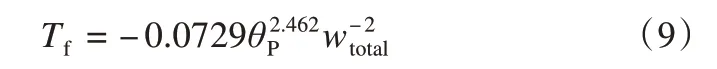
式中:θp为土壤塑限(%)。Kozlowski认为残余水含量与土壤质地和结构等有关,并通过实验证明,残余水含量θres和比表面积S之间存在以下关系:

实验结果表明,当土壤温度在0~-1 ℃之间时,土壤中的未冻水含量急剧下降,近似呈线性趋势。因此,当负温接近于0 ℃时,未冻水含量又可以表示为土壤温度的线性函数[41]:
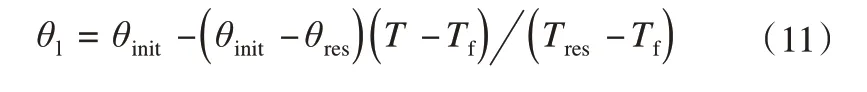
1.4 Bai and Lai(2018)模型
Bai 等[16]考虑到初始含水量和残余水含量,提出一个分段函数模型来预测未冻水含量:

式中:T0为标准状态下自由水的冰点,σ为模型的拟合参数。该模型可用于不同初始含水量的土壤。
2 研究方法和材料
2.1 新的冻融特征曲线模型
在融土中,随着土壤含水量的变化,土壤水吸力也会发生变化[42]。与冻融特征曲线的定义类似,土壤含水量与土壤水能量状态即土壤水的基质势之间的曲线关系被称为土壤水分特征曲线(SWCC)[36],是土壤持水特性的表征。很多学者已比较了SFTC和SWCC之间的相似性[14-15,23,43-45]。早在20世纪60年代,Koopmans和Miller[17]就证实当土壤水分完全由毛细管力或吸附力控制时,SWCC 和SFTC 之间存在平行关系;Black 和Tice[40]的研究表明,在饱和土体下,相同密度和体积的土壤的SWCC和SFTC可进行定量比较,有学者结合Clapeyron与SWCC 导出了非饱和土壤中的SFTC[36]。基于归一化的无量纲土壤含水量与土壤基质势之间的关系可表示为[18]:
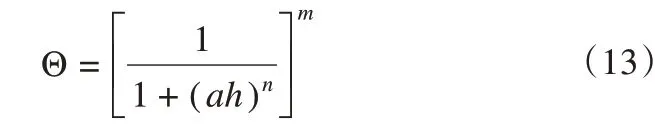
式中:a、n、m为未确定的参数;m= 1-1/n;h为土壤基质势;用压力水头表示;Θ可由下式计算:

式中:θ、θr、θs分别为实际含水量、饱和度和残余水含量。联立式(13)和式(14),即可得到土壤水分特征曲线的Van Genuchten[37]表达式:

注意到土壤冻融特征曲线和水分特征曲线之间的相似性:(1)都是描述土壤液态含水量随土壤某个物理量变化的函数;(2)长期的实验数据表明,土壤SFTC 的变化特征同SWCC 相似(图1);(3)冻结-融化过程的SFTC 和脱湿-吸湿过程中的SWCC都会产生滞后现象[42-43];(4)SWCC 中土壤含水量居于残余水和饱和水含量之间,类似地SFTC 中未冻水含量居于残余水和冻土中初始含水量(或总含水量)之间。因此,归一化理论同样可以用于描述SFTC:

式中:θinit、θres分别为初始含水量和残余水含量(cm3·cm-3);θl为未冻水含量。将式(15)中的自变量h替换为温度T,即得:
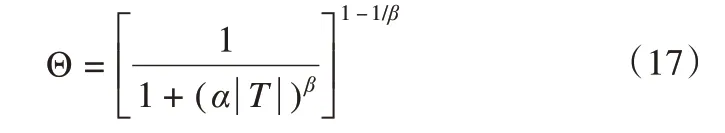
由式(16)和(17)即可导出形式类似于Van Genuchten[18]的归一化公式:

式中:θinit、θres分别为初始含水量和残余水含量(cm3·cm-3);T为温度(℃);α、β为模型的拟合参数。
未冻水含量的变化是多种因素综合作用的结果,以往的模型大都忽略了初始含水量和溶质浓度的影响。然而研究表明,当土壤冻结时,随着土壤水分逐渐向冰相的转变,土壤溶液的浓度会增加(假设冰相中不含溶质),溶质的存在会降低土壤水分的凝固点,从而影响未冻水含量[47]。此外,冻融过程中土壤的凝固点还会随初始含水量的增加而升高,随溶质含量的增加而降低[10,21,48-50]。在式(18)中,我们考虑到土体初始含水量θinit的影响,等式中的两个参数α、β或许能解释溶质浓度对未冻水含量的影响,下文将进行参数α、β敏感性分析,以探索其具体物理意义。
2.1.1 对参数α敏感性分析
如图2(a)显示,若保持初始含水量不变,当固定参数β不变时,α的变动导致了整个模型曲线发生变化。保持参数β等于2.0 不变,令α分别取0.5、1.0、2.0、3.0、5.0。随着α的增加,曲线整体下凹并向左移动。结合图2(b)可以发现,新模型曲线随参数α的变化规律与新模型在不同溶质浓度土壤中的曲线变化规律相似这表明参数α或许和土壤溶质浓度有关,随着溶质浓度的增大,α逐渐减小。

图2 式(18)中参数α的敏感性分析(a);式(18)在不同溶质浓度土壤中的曲线变化(b)Fig.2 Unfrozen water content changing with temperature for various α in the Eq.(18)(a)and for various solute concentration of the Eq.(18)(b)
2.1.2 对参数β敏感性分析
保持α固定不变,曲线随参数β的变化如[图3(a)]所示,保持α等于2.0 不变,令β分别取1.2、1.5、2.0、3.0、5.0,从图3 中可以看出,随着参数β的增加,土壤冻融特征曲线向下移动。保持初始含水量不变,曲线的最低点,即残余水含量随β的增加而减少。结合图3(b),在相同初始含水量下,随着黏粒含量的减小,残余水含量也越来越低,表明β的取值可能同土质有关。受土壤物理性质(如比表面积、干密度、黏粒含量等)的影响,黏粒含量越小,β越大。另一方面,参数β的增加使得冻融特征曲线在0~-2 ℃的温度范围内变得越来越陡峭,当β取到5.0 时曲线几乎垂直。这与图2 中曲线随α的变化规律相似,说明参数β同样与溶质浓度有关。

图3 式(18)中参数β的敏感性分析(a);式(18)在不同质地土壤中的曲线变化(b)Fig.3 Unfrozen water content changing with temperature for various β in the Eq.(18)(a)and unfrozen water content changing with temperature for various soils with different textures of the Eq.(18)(b)
对参数α、β的敏感性分析表明,α受溶质浓度的影响,β则与土质和溶质浓度之间存在联系,可以据此建立相关的参数转换函数来计算不同土壤中α、β的值。
2.2 数据的来源与处理
为了验证新模型的可行性及研究模型中参数α、β的实际物理意义,本文引用了文献中已有的试验数据(见文后附表1),进行参数的拟合与模型效果的评价。在进行数据筛选时需要考虑到:1)数据的完整性。必须要能获取到完整冻结或融化过程的数据资料;2)数据的多样性。所选择的数据需要来自于尽可能多的土壤,便于模型验证;3)优先选择土壤物理性质比较详细的数据。如土壤比表面积、黏粒含量、容重、孔隙度等,便于模型参数物理性质的分析。基于以上原则,本文所选土样数据包括Smith 和Tice[51]文中的6 种粉质土(Hot Springs 粉土、Leda 粉土、Suffield 粉质黏土、Niagara 粉土、兰州粉土),11 种黏土以及4 种代表性土壤矿物组分(膨润土、高岭石、锂辉石、砾石)的冻结实验数据;Spaans 和Baker[52]文中分别处于干燥和湿润两种状态下Waukegan 粉砂土的冻结试验数据;Suzuki[10]中湿地土壤的数据;Wen 等[53]青藏高原粉质黏土的冻结试验数据;Christ 和Park[54]砂土、粉砂土、粉土的试验数据;Wang 等[55]中Harbin 黏土、Lanzhou 黄土以及Ma 等[56]粉土和黏土的冻结实验数据(数据选用的详细信息见附表2)。
考虑到模型效果评价的合理性,将以上所有数据按照来源和土壤类型整理后分为两组,其中一组包含70%的数据,用于模型的训练和参数拟合,另一组包含30%的数据,用于模型的验证和评价。此外,本文还选取了Patterson 和Smith[57]粉质黏土的冻结实验数据以研究模型是否适用于不同溶质浓度的土壤中。该数据包含4 个对照组,即分别用0、10、20、35 g·L-1NaCl溶液饱和,然后进行冻结处理,得到不同溶质浓度下的冻结试验数据。在本文中,同样将其分为训练和验证数据两部分。
2.3 参数拟合预评价指标
本文重点研究新模型的可行性及适用范围。通过对实验数据的分析,研究新模型能否适用于不同的饱和度和不同含水量的土壤中,检验新模型在不同类型土壤中的表现,前文中提到的五种模型被用于模型间的比较。此外,文中还讨论了模型中参数的变化对拟合结果的影响。通过MathCAD(Prime 3.0,Parametric Technology Corporation),利用非线性最小二乘算法来进行参数α、β的拟合。
采用表1所示三种模型评价指标对模型性能进行评价:(1)均方根误差(RMSE),用于衡量预测值与真实值间的偏差,反映测量的精密度。均方根误差的值越小越好;(2)平均偏差(AD),用于来测定预测值与真实值算数平均值间的差异;(3)纳什效率系数(NSE),用于模型的效率评价和对拟合结果的评判,NSE 的变化范围从-∞~1,其值越接近1,则模型的可信度越高,预测值越靠近真实值。此外,文中还给出了各模型在部分土壤中预测值与实测值的1∶1线性图以便更直观地展示测试数据和模型预测值之间的差异。

表1 复合介质混合模型的性能评价指标Table 1 Performance evaluation indexes of the composite medium hybrid model
3 模型评价
3.1 新模型在不同类型土壤中的表现
使用文献中已有的实验数据拟合参数α、β以研究新模型在不同的类型土壤中的适用情况。图4展示了新模型在7 种代表性土壤中的拟合结果,其中粉土和粉砂土是Christ 和Park[54]的野外实验数据;Harbin 黏土来自Wang 等[55],其余四种土样均来自文献Patterson[58]。从图4可以看出,对于这7种土壤样品,用新模型所得到的拟合曲线结果与实测值较为吻合,纳什效率系数(NSE)都在0.95 以上,这表明新的模型可广泛适用于不同类型土壤中。
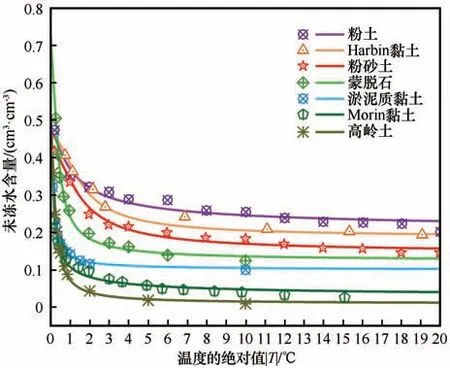
图4 不同土壤中未冻水含量与随温度变化的拟合曲线,其中散点为实测数据,实线为式(18)计算的模拟值Fig.4 Unfrozen water contents of various soils changing with temperature,where the dots are measured data and lines are calculated value by the Eq.(18)
表2 给出了相关的拟合指标,均方根误差(AD)表明,在大部分土样中,预测值稍低于实测值,但在统计学意义上误差均在可接受范围内。尽管不同土壤中模型参数有所差异,但对于给定的土壤,只要能通过实验数据得到参数α、β的值,新模型就能准确预测相同条件下该种土的土壤冻融特征曲线。
3.2 新模型不同初始含水量下的表现
为了研究新模型在不同初始含水量土壤中的表现,本文选用了Wang等[53]的实验数据。土样是来自青藏高原的粉质黏土,比表面积为8.12 m2·g-1,干密度1.56 cm3·cm-3,保持其他条件不变,设置土壤初始 含 水 量 分 别 为0.254、0.313、0.357、0.398、0.459 cm3·cm-3,分别拟合出每个初始含水量下的参数α、β的值,然后通过该参数去计算所有初始含水量下的冻融特征曲线,观察其差异性。从图5 中可以看出,同一土壤分别在五种初始含水量下得到的模型参数对整体的拟合结果并显示出没有出现太大的差异,但相对来说,在初始含水量较低的条件下得到的模型参数在拟合整体时会更准确一些。表3 显示不同初始含水量下得到的参数α、β值不同但差异较小,而且随着初始含水量的变化β和α并没有表现出明显的线性的变化规律。总体来看,预测结果较好地吻合了实测值。表3给出的相关拟合指标显示,模型的NSE都在0.96以上,也就是说,在任意土壤类型和初始含水量下得到的模型参数都是有效的。

图5 不同初始含水量下新模型的表现,散点为实测数据,实线为新模型的模拟结果Fig.5 Unfrozen water content changing with temperature for various θinit(Note:the scattered points are observed and the solid lines are simulated of the new model)

表2 新模型在7种土壤样本中的参数α、β 及拟合指标Table 2 A summary of the parameters α、β for the seven soils and performance measures of the new model to fit the 7 soils samples
3.3 新模型在不同溶质浓度下的表现
本文选择Patterson 和Smith[57]粉质黏土来进行模型在不同溶质浓度条件下的检验,土样干密度为1.19 g·cm-3,保持初始含水量0.523 cm3·cm-3不变,取溶质浓度为10、20、35 g·L-1NaCl 溶液,设置0 g·L-1NaCl 溶液作为对照。图6 为式(18)在不同浓度溶液中的表现,从图中可以看出,模型在低浓度时的表现依旧能很好地同实测值吻合,但随着溶质浓度的增加,拟合曲线逐渐偏离实测值,且浓度越大,预测值与实测值的差异越大,可能是因为该等式同样没有包含溶质浓度对土壤水分凝固点降低的影响,考虑到这一点,引入一个新的参数Tf,式(18)可变为:
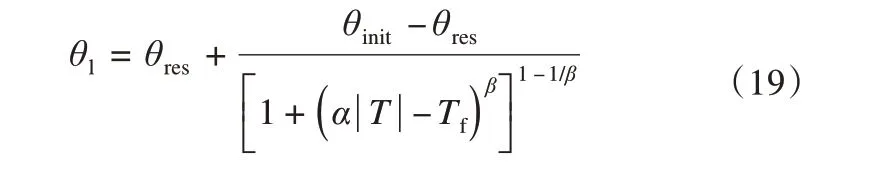

图6 式(18)在不同浓度溶液中的拟合情况,散点为实测值,实线为新模型模拟结果Fig.6 Unfrozen water content changing with temperature of different solute concentrations of the Eq.(18)(Note:the scattered points are observed,the solid lines are simulated by the new model)
Tf表示土壤水分凝固点的降低,在模型中有两种含义:(1)类似于α、β,看作一种拟合参数,没有实际的物理意义;(2)表示土壤水分凝固点随溶质浓度的降低,具有实际的物理意义,并且有相应的计算公式。本文考虑到两种情况,对比作为参数拟合得到的Tf和作为变量计算得到的Tf,选出最适合的模型形式。
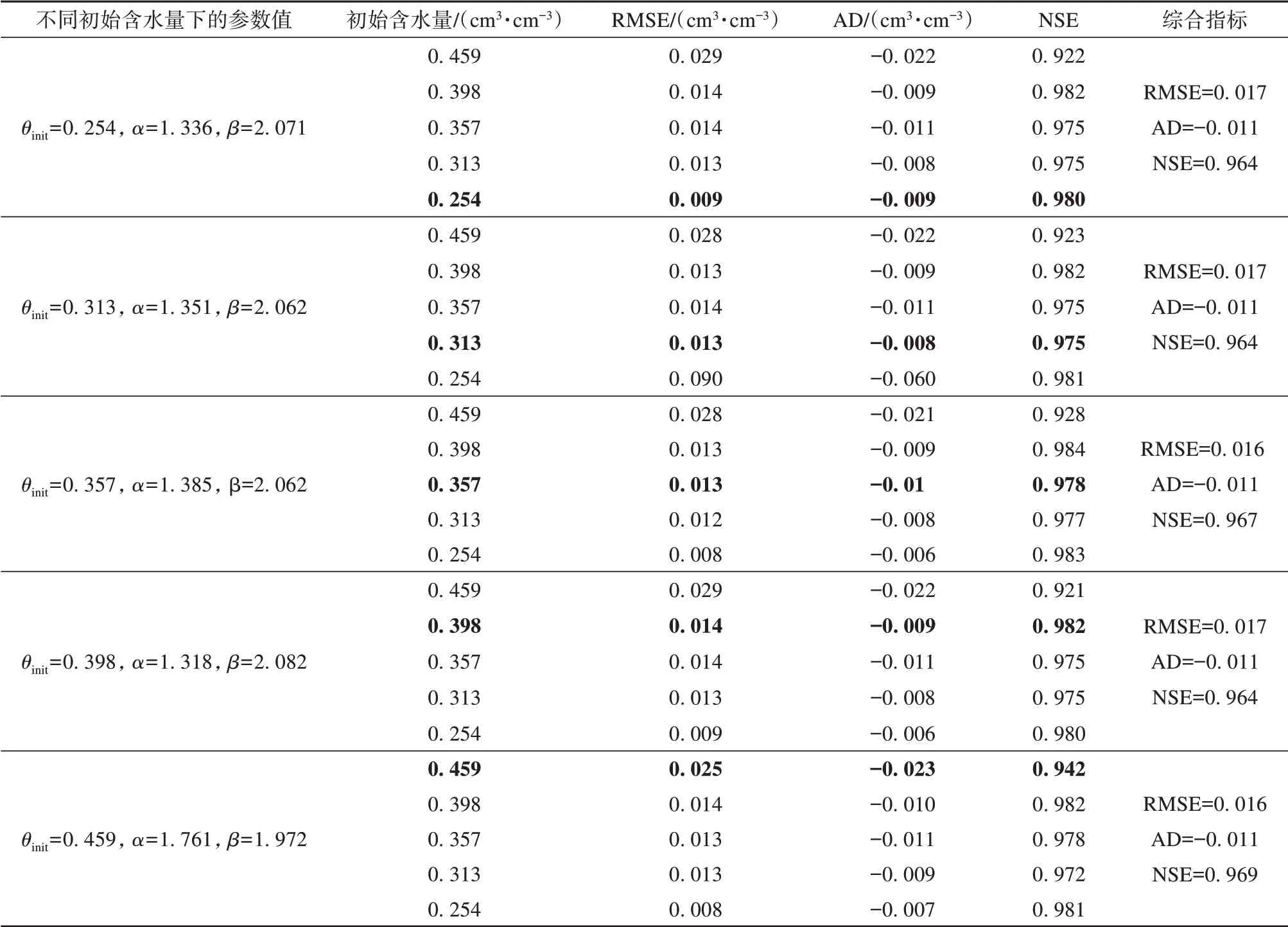
表3 五个初始含水量下分别得到的参数α、β值及其在不同初始含水量情况下的统计指标(加黑数值表示该含水量下对应的指标值)Table 3 The values of parameter α and β corresponding to the five initial water content θinit and their statistical indexes(Note:the corresponding index under initial moisture content θinit is indicated in bold type)
计算Tf的经验公式有很多,Banin 和Anderson[49]描述了土壤中溶质的存在会降低冰点温度,随着土壤水分的冻结,溶质逐渐被滞留在越来越小的空间中,其中,凝固点的降低Tf与溶质浓度之间存在以下关系[59]:

式中:Tref为参考温度,与溶质种类有关,NaCl 可取62 ℃[31]。Sn为溶质浓度(g·L-1NaCl)。Kozlowski[9]修改了式(9),给出了另一种计算Tf的方法:

式中:w为重量含水量(%);wL为土壤液限(%)。此后,Kozlowski[60]又提出可根据土壤干密度和初始含水量来求得Tf:

式中:α和β为给定土壤的系数,是一个常数。Bodnar[61]根据试验数据,回归出了一个三次多项式来描述Tf与溶质浓度的关系:

用上述四种方法计算Tf,并分别与新模型耦合。表4显示四种经验公式的拟合结果在统计学意义上相差不大,考虑到经验公式的不确定性,新模型采用第一种方法[式(21)]来计算Tf值。图7显示在加入Tf后,低浓度条件下,拟合曲线并未有太大变动,但在溶质浓度较高时,式(19)的拟合结果明显要优于式(18),而且相比于用经验公式计算的Tf值,参数拟合得到的结果要更加精确(表5),而浓度为35 g·L-1NaCl溶液的样本在三种方法的计算下NSE都没有超过0.9,这可能是由于在高浓度条件下,实测数据的不准确所导致。

图7 加入Tf后的新模型在不同浓度溶液中的拟合情况,Tf用经验公式和参数拟合两种方法获取。其中实线未考虑Tf影响,短划线Tf通过经验公式计算,虚线的Tf通过拟合获得Fig.7 Unfrozen water content changing with temperature while considering effects of Tf under different solute concentrations(Note:solid line is not considered the influence of Tf,short line Tf is calculated by the empirical formula and the dashed line Tf is obtained by fitting)
综合来看,使用式(18)和式(19),均能准确地描述不同溶质浓度下的未冻水含量随温度变化的关系,但式(19)能更好地反映出溶质浓度的变化对土壤凝固点降低的影响。因此,在实际应用过程中,当土壤溶质浓度较低时,可直接通过式(18)得到准确的冻融特征曲线,而当土壤溶质浓度较高时,通过给模型加入Tf[式(19)]可有效提高其拟合精度。

表4 四种经验公式计算的Tf值在不同土壤溶质浓度下的表现,其中参数α、β通过公式(19)拟合得到Table 4 The statistical indexes of the four empirical formulas calculating the Tf at different soil solute concentrations,of which the parameters α,β are fitted by the Eq.(19)

表5 式(18)和式(19)在不同溶质浓度土壤中的拟合指标,式(19)中Tf的值分别用经验公式(20)计算和参数拟合Table 5 The statistical indexes of Eq.(18)and Eq.(19)in different soil solute concentrations,the values of Tf in Eq.(19)are calculated by the Eq.(20)and by parameter fitting,respectively
3.4 模型间的对比
本文选择了前文中提到五种较为典型的模型与新模型对比,包括两种线性模型[15-41],两种分段函数模型[14]以及早先提出的指数模型[20]。四种土壤(包括砂土、粉砂土、粉土、哈尔滨黏土)被用于对比,砂土、粉砂土、粉土以及一种哈尔滨黏土。其中粉土、粉砂土及砂土冻结数据均来Christ 和Park[54],冻结过程未冻水含量的测定方法为时域反射仪(TDR)法;哈尔滨黏土数据来自Wang等[55],测量方法为核磁共振法(NMR)。
图8 和表6 显示了各模型在四种土壤中的拟合结果。在砂土中,除了Zhang等[41]的线性模型外,其余五种包括新模型都能较为准确地描述未冻水含量和温度之间的关系。在其他三种土壤中,新模型的拟合精度最高,Bai 等[16]的模型次之,Anderson等[20]的预测结果与实测值偏离最大,预测值往往低于测值,且随着土壤黏粒成分的增加和土壤颗粒半径的减小,偏离值增大,可能是由于该模型忽视了初始含水量,只考虑到了土壤比表面积的影响所导致的。Zhang 的线性模型考虑到了初始含水量,其曲线的斜率与初始含水量和残余水含量有关,因此相对于观测值,该模型在未冻水含量接近残余水含量之前总是显示出过高地估计。总体上看,除了新模型和Bai 的模型外,其余模型在应用到砂土以外的土壤中时均会较大程度地偏离真实值,而且随着土壤颗粒级配的变化这种差异也会越发显著。此外,部分土壤样品被用来拟合模型的1∶1散点图(图9),研究预测值和实测值之间的差异。从图9 可以看出,在所有的土壤样品中,新模型的预测值都非常接近真实数据。其他模型中,Bai 模型的表现良好,预测值与真实值也较为接近;Kozlowski 模型由于可用数据太少,无法得出准确结论,但从图中拟合结果来看,在砂土和粉砂土中表现较好。Anderson 模型在未冻水含量较低时表现较好,在较高的未冻水含量下则出现明显的偏离。
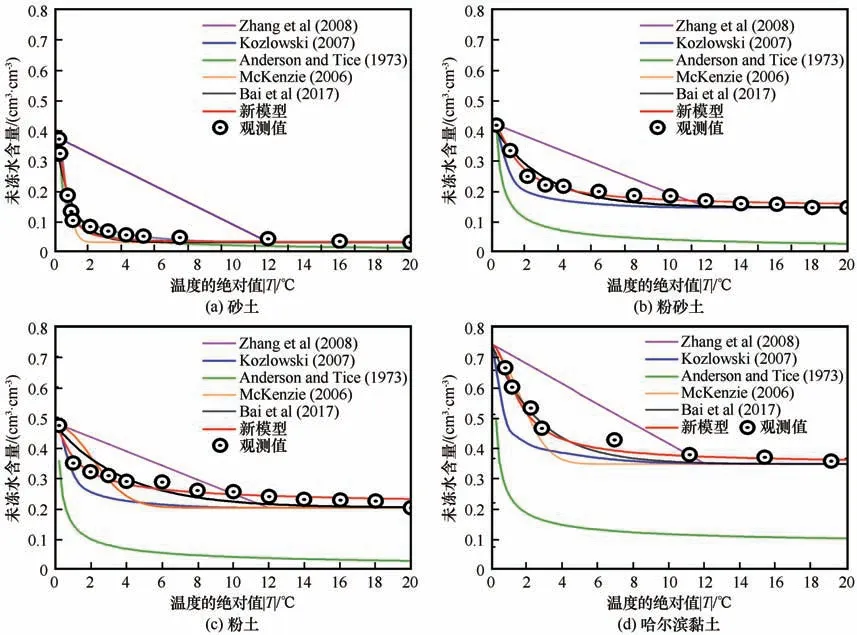
图8 新模型与另外五种模型分别在砂土、粉砂土、粉土及黏土中的表现Fig.8 Unfrozen water content changing with temperature for sand(a),silt-sand(b),silt(c)and Harbin clay(d),measured and simulated by the new model and other five quoted models

图9 6种模型在部分土壤数据的预测值和实测值1∶1散点图Fig.9 The 1∶1 scatter plots of unfrozen water content simulated by the new model and the other five quoted models against the measured
4 结论
本文考虑到初始含水量和溶质浓度对冻融特征曲线的影响,类比水分特征曲线模型,提出一种包含两个参数的新冻融特征曲线模型。利用7种典型土壤样本对模型适用性进行了验证,结果表明新模型可适用于任意类型和饱和度的土壤中。通过加入新的参数Tf,可在统计学上显著提高模型在高溶质浓度条件下的预测精度。此外,明确模型参数α和β在模型中的物理意义有助于模型的完善和应用,敏感性分析表明,参数α与土壤溶质浓度有关;参数β与土壤溶质浓度和土壤自身性质如比表面积、干密度和黏粒含量有关,可根据这些影响因子可建立参数转换函数,方便模型在实际中的应用。由于收集数据的不完整,本文未能建立有效的参数转换函数,但给出了用于测试模型的38种土壤样品的参数值(附表1)以供参考。
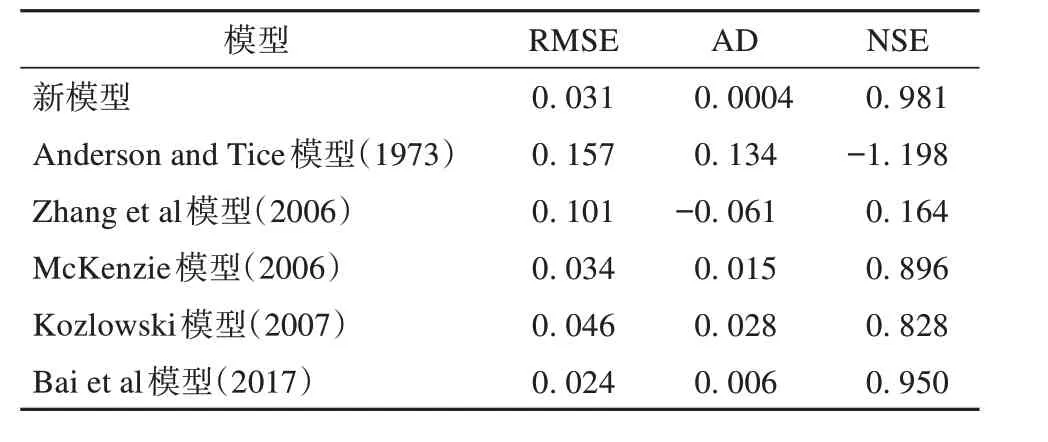
表6 新模型和其他五种模型的拟合指标Table 6 The statistical indexes of the new model and the other five quoted models

附表1 38种土壤样品的参数α和β值及模型拟合指标Attached Table 1 The parameters α and β of the 38 soil samples,together with determination method and index

附表2 土样数据的来源、测定方法和基本性质Attached Table 2 Sources,determination methods and basic properties of the soil samples
