基于最大熵原理的四川省干旱灾害致灾危险性研究

杨庭潇 ,马 力

（1.成都信息工程大学，成都 610225；2.四川省气象局，成都 610072）

引言

四川省位于中国西南内陆，气候差异显著，降水主要受季风影响，近年来旱涝灾害发生频率呈逐年升高趋势，仅2010年干旱造成全省共计13.8亿人民币直接经济损失。当一次灾害性天气过程发生后，四川省防办曾问过四川省气象局该次灾害过程与其他时间同类灾害相比强度如何的问题。参考地震灾害的地震量级表征其致灾能力以及过去学者选取暴雨降水量因子利用总体主成分和阈值法研究得到暴雨致灾能力评估指数思路[1−2]，可研究四川省干旱灾害致灾危险性指数以表征一次干旱灾害过程的致灾危险性大小即其灾害强度，并可以此解答此类问题。同时，研究干旱灾害致灾危险性作为干旱灾害风险评估的前期基础工作，能从气象角度首先定量说明一次干旱过程的灾害影响能力大小，有利于提高后续灾害风险评估工作精准度，减小气象服务效益评估及干旱灾害相关保险产品制作等工作的难度。

现有的气象灾害风险评估研究工作常利用地区脆弱度、暴露度等综合要素进行风险评估，资料跨学科收集难度较大，且未首先从气象角度说明其具体强度，最终评估结果精准度较差、地区局限性较大[3−5]。气象学者对于干旱灾害的相关研究多集中于农业干旱和区域单品种干旱灾害特征研究，而从气象角度出发的对干旱过程的灾害影响研究较少，且气象干旱评估指标繁多，运用效果各有千秋，其中标准化降水指数（SPI）运用较多，并经过多年研究后提出了改良的气象干旱综合监测指数(MCI)[6]。目前，已有研究利用SPI指数、Z指数、K指数以及MCI指数对四川省干旱过程进行了评估，结果表明MCI指数更适用于四川省干旱灾害监测及评估分析[7−13]。起源于19世纪统计物理的熵概念，20世纪开始运用于信息论中，目前已广泛运用于医疗、运动等领域研究中，而自上世纪九十年代初气象学者创立熵气象学后，其在气象领域运用却较少，近年仅少量学者将其运用于解决闪电时程方程中雷暴过程闪电总量与闪电频次关系的分布函数问题。最大熵原理是一种选择随机变量统计其特性最符合客观情况时的准则，世间万物最终呈现状态均符合最大熵原理所揭示的规律，即为熵最大、出现概率最大时的状态，由最大熵原理推导的分布规律是具有普适性的规律，熵原理对大气亦有普适性，其在气象领域具有宽广光芒的应用前景[14−24]。本文利用最大熵原理推导干旱重要气象要素概率分布规律，根据其概率分布规律，延续过去学者干旱评估及致灾能力评估研究思路，选取最适宜气象要素与相应灾害损失分别计算其关联度，最终得到四川省为例的干旱灾害致灾危险性指数，作为干旱灾害风险评估的前期基础工作，可从气象角度首先清晰定量提供其致灾危险性大小。

1 数据和方法

1.1 数据

研究所用气象数据包括四川省气象台提供的全省所有加密自动气象观测站的逐日平均气温、逐日累计降水量数据以及国家气候中心提供的经过处理计算的四川省所有站点逐日MCI值数据，时间长度为2006～2020年。所用灾害损失数据来源于四川省气象台决策服务中心提供的四川省内各市州每日上报的由于各类自然灾害如暴雨、干旱、地震、森林火灾等所造成的实际灾害损失灾情统计数据，时间长度为2006～2020年。

1.2 主要方法

本文首先利用最大熵原理推导干旱过程中重要要素的概率分布规律，若能通过相关检验，则推导正确，可根据其概率分布规律选择最适宜于研究干旱灾害致灾能力指数的气象要素，利用序列关联度方法分别分析各要素与实际灾害损失之间的关联度，再依据不同要素关联度大小计算其权重，制定出干旱灾害致灾能力指数。所得到的干旱灾害致灾能力指数能用于评估一次干旱过程的致灾能力大小，根据其具体气象要素带入指数公式所得到的值越大，其致灾能力就越强。选择实际灾害损失不同的干旱个例对致灾能力指数进行检验，若能正确反映其致灾能力，则公式正确。

对干旱相关气象要素的概率分布规律推导选用最大熵原理方法，选取一定时段内不同无雨期长度与对应持续时间出现频率作为干旱过程重要参考气象要素，利用最大熵原理推导其概率分布规律，应首先将离散变量无雨期长度x分立为若干个值，每个值有相应的概率p与之对应，如表1所示：

表1 变量与概率对应表

2 概率分布规律检验

由于最大熵原理能在信息不完整情况下最大限度排除主观因素干扰，通过其所确定的分布规律为最公正的预测结果，在复杂系统的无限种概率分布情况中其可信度最高。且分布函数不同于其他统计模型，其包含的统计要素最为全面，能综合各统计要素以全面说明对象的状态。基于最大熵原理所推导的无雨期长度与对应持续时间的对数线性分布规律应是具有普适性的，其克服了时间、空间上的局限，故可仅用少量个例对其进行检验，若均能通过，则推导结果正确，可普遍适用，运用于以代表干旱过程的强度以解决相应问题。在所用数据资料中，选取符合四川省干旱标准的，例如2006年伏旱、2007年夏旱、2020年春旱等强度不同、发生时段不同的干旱个例，统计其数据进行概率分布规律检验。首先依次分别统计所选每次过程中不同无雨期长度占总时长的频率，再计算其对数并进行线性拟合，最后利用F检验方法考察线性拟合结果能否通过0.05水平的显著性检验。所选概率分布规律检验干旱过程中一次过程的无雨期与对应频率的对数的线性拟合情况如图1所示。

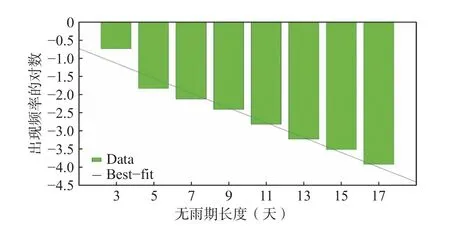
图1 一次检验个例的无雨期长度与出现频率对数的线性拟合情况

使用F检验方法考察个例时，首先均假设H0：b=0，数据若做出拒绝原假设b=0的判断，则线性回归模型合理。将不同无雨期长度出现频率的对数即变量y的离差平方和进行分解，得到回归平方和，进而得到误差平方和式中y为不同无雨期长度出现频率的对数，n为无雨期长度按2天为差值的分组数量），则对给定的显著性水平α，每组个例均可查相应自由度为（1，n−2）的F分布临界值表，可得临界值Fa，若计算所得F>Fa，则拒绝原假设，显著性通过，线性分布成立，则无雨期长度与其对应出现频率的负指数分布也应成立。所选个例按上述方法计算所得的部分F值及相应临界值如表2所示：

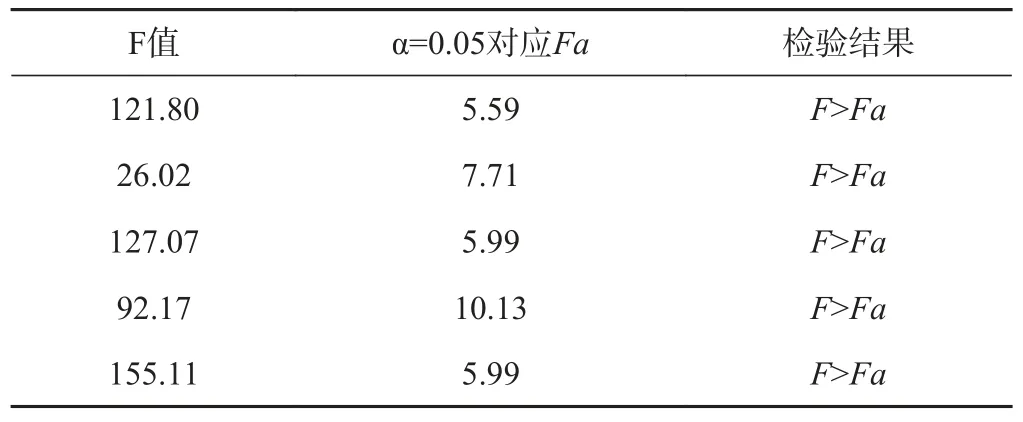
表2 部分个例检验情况

所有个例的F值均远大于查表相应Fa值，均可通过0.05水平的显著性检验，线性拟合正确，线性分布规律存在。故由最大熵原理所推导的无雨期长度与出现频率的对数的线性概率分布规律成立，即无雨期长度与出现频率的负指数概率分布规律也应成立。由最大熵原理推导的具有普适性的无雨期长度这一概率分布规律可用于干旱相关研究，可以寻找适用于干旱相关评估研究的要素。

3 致灾能力指数

3.1 要素选取

根据最大熵原理推导所得概率分布规律，一定时间段内地区的无雨期长度与出现频率为负指数关系，则无雨期长度概率分布形式函数中仅有数学期望这一主要参数，影响无雨期长度出现频率的概率分布函数形式有且仅有一个主要的约束条件。综合最大熵原理所推导降水其他要素的概率分布规律均呈指数簇形式，在降水相关评估研究中，要素选取仅用时间、面积、强度相关要素即可较好代表干旱过程整体情况[20]。在干旱众多气象评估指标中，改良后的气象干旱综合指数（MCI指数）能更好地满足业务需求，更适用于四川地区，故选用MCI值、持续时间、覆盖总面积、温度距平、无雨日、无雨面积六个要素作为研究干旱灾害致灾危险性的气象要素。其中，持续时间是地区达到干旱标准开始至地区不再符合干旱标准为止的累计时间，不计其中≤3d的不符合干旱标准的中断时间。干旱覆盖总面积是干旱持续时间内所有符合干旱标准的站点所代表的覆盖总面积。MCI值选取干旱持续时间内所有符合干旱标准站点中逐日值的最小值。为得到温度距平值，首先计算所有符合要求的站点在干旱时段内的平均温度与同时段多年平均温度的差值，再选取干旱范围中心点，各站点温度距平以此进行距离加权平均，即可得地区平均温度距平值，作为反映干旱时段内干旱地区温度异常指标值。无雨日是干旱时段内所有站点中无任意形式降水现象发生的最长累计时间。无雨面积是干旱地区范围内所有在干旱时段内无任何形式降水现象发生站点所代表的覆盖总面积。

3.2 致灾能力指数计算

选取所用数据资料中符合四川省干旱标准的所有干旱过程，过程对应的气象要素及灾害损失数据均首先采用z-score方法进行无量纲标准化处理，以去除不同量纲带来的较大影响，使得数组进行关联度计算时是统一标准。所有无量纲标准化处理后数组的数值值域均为[−1，1]，且数值正负号不具有正负意义，仅代表数值大小。依据最大熵原理所推导的概率分布规律所选一次干旱过程的干旱总面积、MCI值、持续时间、无雨日、无雨面积、温度距平六个气象要素均为一次干旱灾害性过程的重要气象参考要素，应能对灾害损失产生不同影响，其与灾害损失之间均有一定的关联度存在。采用序列关联度方法计算其关联度，其中，选用灾害损失数组作为参考数列，所选六个气象要素数组作为比较数列。利用序列关联系数公式其中，∆min为第二级最小差，∆max为第二级最大差，∆ok为比较序列点与参考序列对应点绝对差）以及序列关联度公式分别计算经过无量纲标准化处理后的六个气象要素与灾害损失参考数列之间的关联度，最终得到干旱覆盖总面积与灾害损失关联度为r1=8.35，MCI最小值与灾害损失关联度为r2=7.38，持续时间与灾害损失关联度为r3=7.96，无雨日与灾害损失关联度为r4=8.60，无雨面积与灾害损失关联度为r5=6.60，温度距平与灾害损失关联度为r6=6.60。干旱覆盖总面积与灾害损失关联度最大，其对一次过程所能带来的灾害损失影响最大；无雨面积与温度距平与灾害损失关联度最小，在一次灾害性干旱过程中其对灾害损失的影响最小。

所选气象要素对灾害损失均能带来影响，但影响大小各不相同，根据所得气象要素与灾害损失之间关联度，可进一步计算得到一次灾害性干旱过程中干旱总面积、MCI值、持续时间、无雨日、无雨面积、温度距平六个气象要素实际值对所产生灾害损失的影响权重分别为：19%、16%、17%、20%、14%、14%，则可得到干旱致灾危险性指数为其中分别为无量纲标准化后的一次干旱过程的干旱总面积、MCI值、持续时间、无雨日、无雨面积、平均温度距平六个气象要素。由于所用要素均须经无量纲标准化处理，则所得干旱致灾危险性指数值域也应为[−1，1]，且正负不具意义仅代表大小。所得到的干旱致灾危险性指数可运用于四川省干旱灾害风险评估前期工作，以说明一次干旱过程的致灾危险性大小，致灾危险性指数值越大，则该过程致灾能力越强，所带来灾害损失越大。

3.3 检验

对所得的干旱致灾能力指数，选取带来灾害损失大小各不相同的干旱灾害个例代入进行检验，检验其能否正确反映不同个例的灾害强度大小。选取2013年和2015年春季的两次春旱过程以及2010年冬季的特强干旱过程来检验所得致灾能力指数能否正确反映其致灾能力大小。三次干旱过程的主要影响范围与持续时间也均不相同，三次过程的MCI值分布如图2所示。

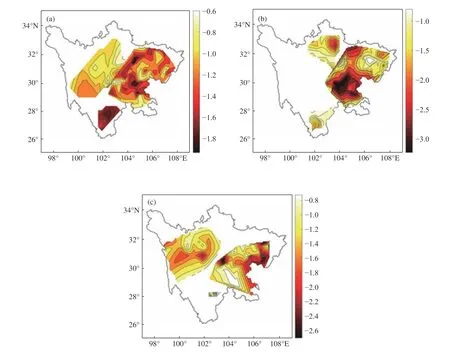
图2 三次干旱过程MCI值分布（a.2010年，b.2013年，c.2015年）

三次干旱过程持续时间、影响范围、MCI值等各不相同，最终造成的累计灾害损失也各不相同，其中2010年共造成全省600多万亩农作物受灾，10.8万亩绝收，直接经济损失达13.8亿元，2013年共造成全省608.9万人受灾，直接经济损失共8.414亿元，2015年所造成灾害损失最小，直接经济损失为2.75亿元。将三次干旱过程的干旱总面积、MCI值、持续时间、无雨日、无雨面积、平均温度距平六个气象要素使用进行无量纲标准化处理后，代入所得干旱致灾能力指数公式中，计算得到2010年、2013年、2015年三次干旱过程的致灾能力指数分别为：H2010=0.601，H2013=−0.040，H2015=−0.075。其中，2010年干旱致灾能力指数远大于其余两次干旱过程干旱致灾能力指数，对比三次过程所造成实际灾害损失影响，2010年灾害损失远大于2013年及2015年，2013年灾害损失略大于2015年，致灾能力指数正确反映出了三次干旱过程的不同致灾能力大小。

对比三次干旱过程的其他干旱指标，如SPI指数值：S2010=−2.1971、S2013=−1.4576、S2015=−0.7114，2010年的SPI值最小，2013年次之。由于SPI指数的负值越小对应干旱程度越强，与致灾危险性指数所反映的2010年致灾危险性最大、2013年致灾危险性次之结果一致。得到的致灾能力指数值能正确定量反映一次灾害性干旱过程的致灾危险性大小，指数值越大的灾害性干旱过程具有更强致灾危险性，所能带来更大灾害损失的能力越强，反之越弱。

4 结论

本文基于最大熵原理推导所得到的干旱相关重要气象要素−无雨期长度与出现频率的概率分布规律呈现负指数形式，选取最适宜于干旱灾害相关研究的气象要素与灾害损失进行关联度计算，得到干旱灾害致灾危险性指数，并对其进行检验。主要结论如下：

（1）利用最大熵原理推导得到一定时间段内不同无雨期长度与对应出现频率之间的概率分布函数应为负指数形式，则其与出现频率的对数之间应为线性关系，且能通过0.05水平的显著性检验，推导结果正确。根据所得概率分布指数形式，主要影响其分布的统计学要素仅为数学期望。

（2）依据最大熵原理推导结果，一次干旱过程的干旱总面积、MCI值、持续时间、无雨日、无雨面积、平均温度距平六个气象要素最适宜应用于干旱致灾能力等干旱相关研究中，能较好的全面反映一次干旱过程的“时、面、深”问题。分析所选取六个气象要素与实际灾害损失之间关联度，干旱总面积与灾害损失之间关联度最高。

（3）经检验，所得到的干旱致灾危险性指数能正确反映不同强度灾害性干旱过程的致灾危险性大小。一次灾害性干旱过程将实际要素值经无量纲标准化处理后带入指数公式，得到的干旱致灾危险性指数值越大，其致灾危险性越高，所能带来较大灾害损失的能力越强，反之，则危险性越低，能来的较大灾害损失的能力越小。可据此研究为基础，进一步提高后续干旱灾害综合风险评估工作的精准度，并减小工作跨学科难度，并能对干旱相关气象服务工作效益评判提供帮助。