堵塞条件下紧密栅湍流交混特性研究

郝思佳，乔守旭,*，祁沛垚，钟文义，谭思超，王啸宇

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

目前许多国家设计的反应堆堆芯都采用紧密布置的棒束燃料元件，这种紧密栅将提高238U的转化率，从而提高燃料的利用率[1]。但由于这种布置形式的棒间距较窄，因此较传统棒束更易发生堵塞事故。堵塞事故会明显改变堵塞下游流场形态，进而影响传热传质特性，因此有必要对紧密栅堵塞工况下的流动情况展开研究。此外，研究堵塞工况湍流交混系数的分布规律，对于子通道分析程序的发展也有一定工程意义。

国内外学者针对紧密栅流体的流动特性已进行了大量实验与仿真研究。Rowe[2]对棒束子通道内轴向速度与湍流强度进行了研究，结果表明，节距比是影响子通道内流动特性的重要参数。Hooper[3]和Rehme[4]发现紧密栅在棒间隙具有强烈的动量能量交换。Lee等[5]采用激光诊断技术对紧密栅流场进行实验研究，结果强调了湍流交混在紧密栅中的必要性。Baglietto等[6]的仿真研究结果表明，各向异性湍流模型可真实再现紧密栅的流动特性。Chang等[7]模拟了37棒束通道充分发展流动，模拟所得速度和雷诺应力结果与实验结果吻合良好。顾汉洋等[8-9]利用不同湍流模型对紧密栅流动进行了仿真研究，结果表明，SSG雷诺应力模型对紧密栅流动有较好的模拟。何斯琪等[10]对紧密栅定位格架下游流场的交混特性进行了仿真研究。

目前有关紧密栅流动的研究主要集中于光棒流场，针对此类型元件堵塞工况流动的研究鲜有报道。因此本文拟采用CFD方法研究不同子通道堵塞对流场及湍流交混系数的影响。

1 几何模型与网格划分

1.1 几何模型

采用完整的通道截面作为计算模型进行三维CFD流动计算，棒外径为15 mm，棒间距为16.4 mm，通道长宽均为84 mm，棒束呈5×5正方形排列，模型总高度为800 mm。此几何尺寸依据文献[11-12]中尺寸范围进行选取，属于紧密栅尺寸范围，在此范围内不同尺寸元件堵塞下游流动的交混系数在数值上会有一定区别，但变化的趋势基本相似并具有一定借鉴意义。模型分为堵塞上游、堵塞段、堵塞下游3部分，并比较3组不同工况。第1组为不同子通道堵塞工况，此工况建立了3种堵塞模型：中心通道堵塞、边通道堵塞、角通道堵塞，3种堵塞长度均为4 cm。第2组为不同堵塞率堵塞工况，此工况建立了3种堵塞模型：子通道100%堵塞、子通道50%堵塞、子通道25%堵塞，3种堵塞长度均为4 cm。第3组为不同堵塞长度堵塞工况，堵塞位置均为中心通道，此工况建立了3种堵塞模型：堵塞长度4 cm、堵塞长度2 cm、堵塞长度1 cm，此3种模型仅长度不同而形状与中心通道堵塞模型相同。每组工况坐标系原点均选在入口截面中心位置，流动方向为y轴正方向，通道几何模型示意图及堵塞模型如图1所示。

分析区域的横截面示意图如图2所示，5×5紧密栅共有60个子通道间隙(G1～G60)，为便于分析堵塞区下游子通道交混特性，选取堵塞位置所处子通道中心连线L1、L2、L3、L4来分析堵塞区下游不同高度处的速度分布。

1.2 网格划分与无关性分析

采用六面体结构化网格进行网格划分，为保证网格无关性，建立了3种网格模型，网格主要参数设置列于表1。湍流模型采用文献[13-15]推荐的SSG雷诺应力模型，该模型考虑了通道中流体湍流流动的各向异性、流线型曲率、应力突变和二次流的影响，能较好模拟紧密栅流动。入口设置为速度入口，出口设置为压力出口，壁面采用无滑移条件，y+值小于5。采用SIMPLEC算法对压力-速度耦合计算，动量方程采用二阶中心差分离散。网格划分示意图如图3所示。

所选取堵塞下游1Dh(Dh为水力直径)处的主要参数示于图4，图4a为横坐标无量纲后的G25位置雷诺应力(uu)对比，图4b为L1的轴向速度W对比。由图4可见，3种方案的预测趋势较为一致，但方案1在计算精度上存在较大误差，方案3计算精度较高但耗时较长。而方案2与方案3的计算结果有良好的符合度，定量偏差较小，综合考虑计算精度与计算代价，选取方案2进行计算。

图1 通道几何模型示意图

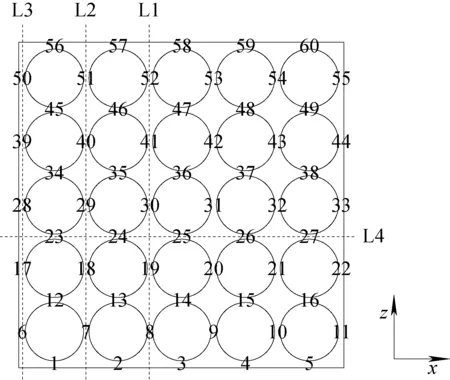
图2 主要分析区域横截面示意图

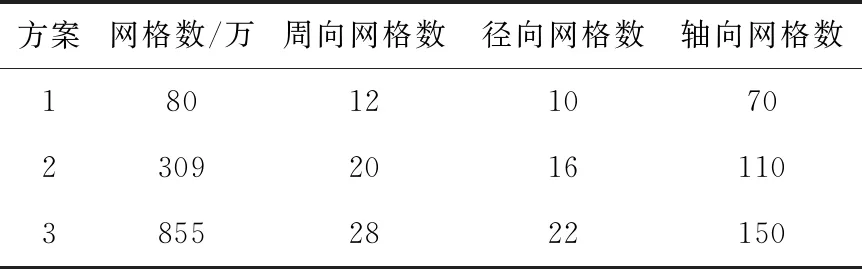
表1 主要网格参数

图3 计算截面网格划分

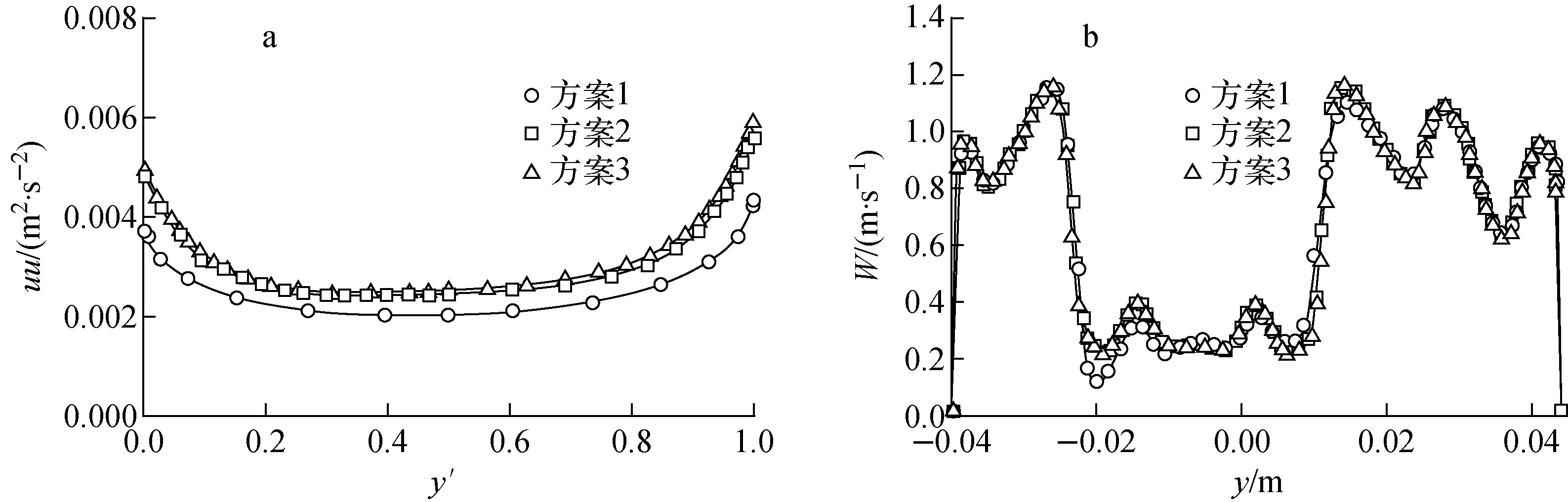
图4 网格敏感性分析

2 分析方法与结果对比

2.1 处理方法与验证

本文主要对湍流交混系数进行分析。所研究的速度工况处于过渡区与湍流区，入口雷诺数Re=3 000、6 000、10 000、20 000、30 000、40 000。参照广泛用于子通道分析程序定义方法来计算湍流交混系数β[16-17]，如式(1)所示。平均速度脉动与雷诺应力的关系由式(2)、(3)计算。不同方向雷诺应力可由脉动速度均方根计算，如式(4)所示。

(1)

(2)

(3)

uu=ρURMSURMS；vv=ρVRMSVRMS；

ww=ρWRMSWRMS

(4)

为验证模拟算法的准确性，将计算结果与相应实验验证结果和现有文献结果分别进行对比。图5a为实验速度与模拟速度对比结果，二者吻合较好。图5b为仿真结果与文献[9]结果的对比。二者通道结构相同，但棒尺寸与节距比(P/D)存在微小差异，为方便对比，横坐标根据棒间隙长度进行了无量纲化，轴向速度根据主流速度进行无量纲化。图中示出了棒周向0°与45°流体的轴向速度，可看出本文仿真结果与文献中的实验与仿真结果均吻合较好。由以上对比计算得出速度的不确定度低于10%。

2.2 不同子通道堵塞交混程度对比

控制不同子通道堵塞作为自变量、堵塞率均为100%，对比了3种子通道堵塞工况，即中心通道完全堵塞、边通道完全堵塞、角通道完全堵塞。

选取过渡流(Re=6 000)和湍流(Re=30 000)两流态下工况速度场结果进行分析。图6为两工况下中心通道堵塞区下游不同水力直径(Dh)轴向速度云图以及L1位置轴向、横向速度线图。图中按与堵塞段距离选取检测的轴向位置，用Dh的整数倍计量，1Dh即为此处距堵塞段出口平面1倍水力直径长度。从影响范围看，堵塞段的主要影响范围是堵塞物周围相邻的子通道，其余子通道的横向速度与轴向速度与光棒流场相差不大。从横向速度在堵塞物下游附近流向相反可知，堵塞物所在子通道相邻子通道流体会在堵塞段下游流向堵塞子通道。堵塞位置下游2Dh处存在回流区域，横向速度在4Dh内会逐渐增加到出现最值，之后会逐渐减小至光棒横向速度。横向速度在约10Dh内恢复较快，之后逐渐趋于光棒分布。从雷诺数的变化看，雷诺数改变不会对堵塞物下游流场分布规律产生明显影响。同时，堵塞物的存在也会导致下游较近位置当地雷诺数减小。

图5 仿真结果验证

图6 流体速度分布

相比于中心通道完全堵塞，边通道完全堵塞工况堵塞段下游流体恢复至光棒速度所需的距离略近，但相差不大。从影响范围看，堵塞段的主要影响范围同样是堵塞物所在子通道及其相邻的子通道，边通道有3个相邻子通道，角通道有2个相邻子通道，速度的主要变化区域集中于此范围内。从轴向看，堵塞位置下游2Dh处存在回流区域，横向速度在4Dh内会逐渐增加到出现最值，之后逐渐趋于光棒速度。从雷诺数变化看，雷诺数改变不会对堵塞物下游流场分布规律产生明显影响。由于主要现象与中心子通道堵塞基本相同，因此结果不再加以展示。

为分析堵塞下游涡结构，提取涡核于图中红线区域，如图7所示。从径向看，涡核所在范围集中于堵塞物下游所在子通道，周围子通道并无涡核存在；从轴向看，中心通道堵塞涡核范围位于堵塞段下游(1～3)Dh范围内，边通道涡核范围位于(0.5～3)Dh范围内，角通道涡核范围位于(0.5～2.5)Dh范围内，反映了3种堵塞工况下游涡核区域逐渐靠近堵塞段，这一现象可能是由于通道壁面效应导致的。此外，不同子通道堵塞物下游的涡分布不同：中心子通道堵塞物下游燃料棒周围存在8个主要的涡结构，边子通道为4个，角子通道为2个。涡的存在主要是由于堵塞物下游周围子通道流体进入堵塞的子通道，流动方向不同的两股流体会在棒壁面与x轴或z轴夹角45°附近交汇，从而产生涡结构。

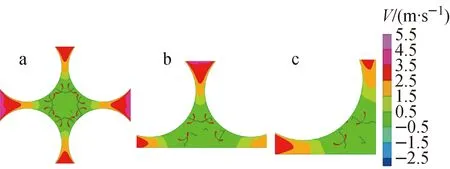
a——中心通道堵塞；b——边通道堵塞；c——角通道堵塞

中心通道堵塞下游不同高度处子通道间隙的湍流交混系数示于图8，所检测子通道间隙位置均标识于图中。在过渡流与湍流区内，雷诺数的改变对下游交混系数分布规律的影响不大，这与前文速度对比的结果相似，雷诺数主要影响正常工况流体的交混系数。定性来看，堵塞物所在子通道间隙(G25)的湍流交混系数会在堵塞下游3Dh内有所升高，这是由于此范围内存在宏观的涡结构，使得此处湍流交混增强。之后湍流交混系数会在约15Dh内快速下降，之后缓慢趋近于正常工况。对于堵塞物所在相邻的子通道间隙(G36)，其湍流交混系数会略高于正常工况，在3Dh内快速下降，之后缓慢趋近于正常工况。对于其余的子通道间隙(G47、G49)，其湍流交混系数会在3Dh内快速下降至接近于正常工况。定量来看，堵塞物所在子通道间隙湍流交混系数最大会增至正常湍流交混系数的3倍左右，其相邻子通道湍流交混系数最大会增至正常工况的1.5倍以内，其余子通道增幅会更低。

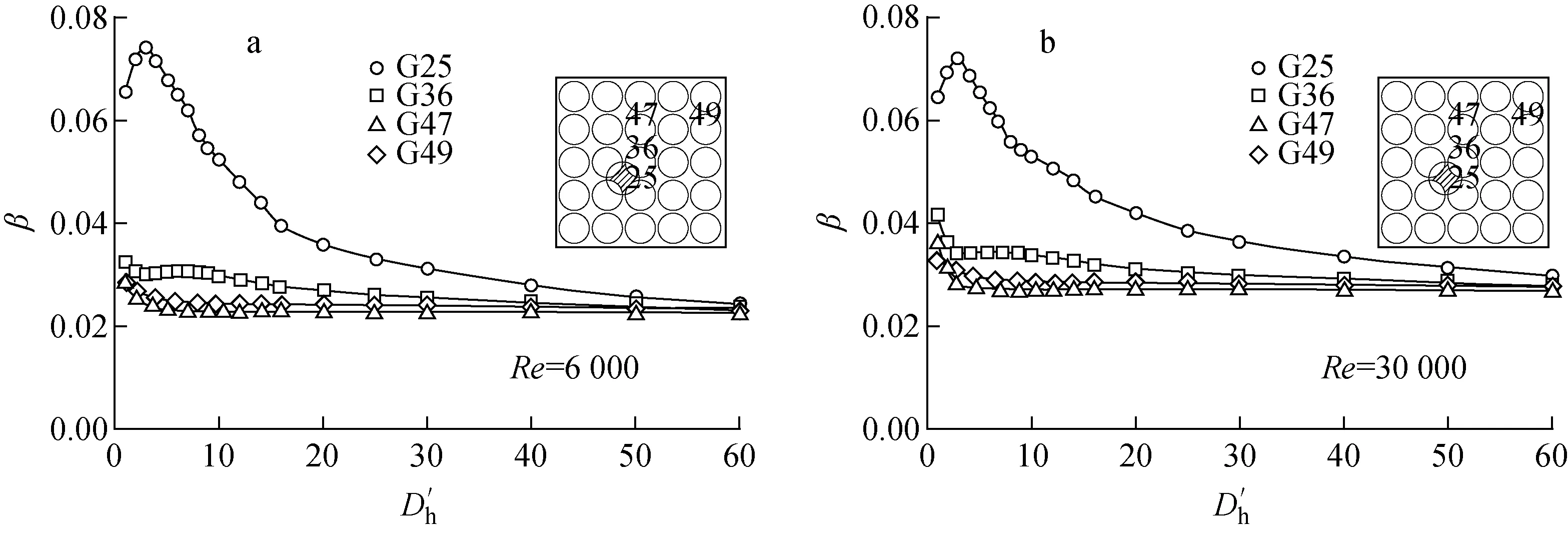
图8 中心通道堵塞下游不同位置交混系数

图9 边通道堵塞下游不同位置交混系数

由于过渡区与湍流区雷诺数的改变对湍流交混系数分布规律影响不大，因此仅将Re=30 000时边通道堵塞下游不同高度处子通道间隙的湍流交混系数进行对比，结果示于图9。堵塞物所在子通道间隙的湍流交混系数会在堵塞下游3Dh内有所增加，其中G7湍流交混系数增长的范围较G2小，这可能是由于两间隙位于不同子通道导致的。相邻子通道间隙(G3、G6、G8、G13、G18)的湍流交混系数，在堵塞下游一定范围内由于所在子通道间隙不同会呈现不同的分布，但总体来说会出现一个最大值之后缓慢下降至正常工况。其余子通道间隙(G16、G24)的湍流交混系数变化规律较为一致，均会在3Dh内快速下降至正常工况。定量来看，堵塞物所在子通道间隙湍流交混系数最大会增至正常湍流交混系数的2倍，增加幅度低于中心通道堵塞，这体现了壁面的抑制作用。

角通道堵塞段下游不同子通道间隙的变化规律与中心通道堵塞、边通道堵塞的变化规律相似，因此不再展示具体结果。定量来看，堵塞物所在子通道间隙湍流交混系数最大会增至正常湍流交混系数的2倍左右，其相邻子通道湍流交混系数最大会增至正常工况的1.5倍以内，其余子通道增加幅度会更低。角通道堵塞相比于中心通道堵塞交混系数增长幅度减弱，这可能是由于通道壁面的抑制导致的。

综上分析，在堵塞下游，堵塞物主要会影响堵塞子通道及其相邻子通道的湍流交混系数，堵塞物所处子通道间隙的湍流交混系数会在堵塞下游增加为光棒湍流交混系数的2～3倍，这一增幅随雷诺数的增加而减弱。若堵塞位置靠近边角通道，则湍流交混会受到通道壁面抑制。

2.3 不同堵塞率交混程度对比

控制不同子通道堵塞率作为自变量，选取的堵塞子通道均为中心通道，对比了3种子通道堵塞工况，即中心通道100%堵塞、中心通道50%堵塞、中心通道25%堵塞。

选取过渡流(Re=6 000)和湍流(Re=30 000)两流态工况下速度场结果进行分析，图10为两工况下中心通道堵塞段及堵塞下游不同水力直径轴向速度云图。从横向影响范围看，堵塞段的主要影响范围同样集中在堵塞物所在子通道及其相邻的子通道，但随着堵塞率的减小，对流场的影响程度与范围也会减小。从纵向影响范围看，随着堵塞率的不断降低，下游流场恢复至正常工况流场的距离更短。在堵塞率较小时，堵塞物周围和堵塞物下游的涡尺度同样会减小，涡的尺度也与堵塞物形状有关。从雷诺数的变化看，在过渡区与湍流区，雷诺数的改变不会对堵塞物下游流场分布规律产生明显影响。同时，随着堵塞率的增加，堵塞下游附近流体的当地雷诺数会逐渐减小，这体现了堵塞物对流场的扰动。

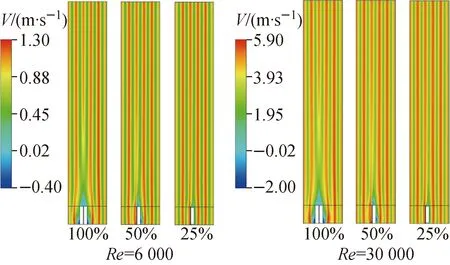
图10 不同堵塞率下的流体速度云图

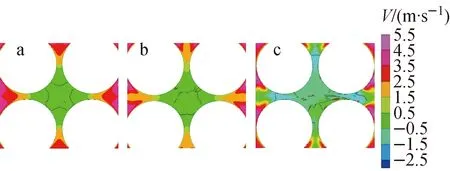
为分析堵塞下游涡结构，提取涡核于图中红线区域，如图11所示。从径向看，涡核所在范围集中于堵塞物下游正下方，其余位置并无涡核存在，由于棒间隙流体的压力较高、子通道中心流体压力较低，因此流体流动的方向主要是由压力更高的棒间隙流体沿棒周向汇入堵塞物正下方区域；从轴向看，中心通道100%堵塞时涡核范围位于堵塞段下游(1～3)Dh范围内，50%堵塞时涡核范围位于(0.5～2)Dh范围内，角通道涡核范围位于(0～1)Dh范围内，这说明随着堵塞率的降低，涡出现的范围逐渐靠近堵塞段，且涡尺度也会随之下降。此外，不同堵塞方式下游的涡分布不同：中心通道100%堵塞时堵塞段下游燃料棒周围存在8个主要的涡结构，50%堵塞时为4个，25%堵塞时为2个，涡出现的形式也与堵塞物形状有关。

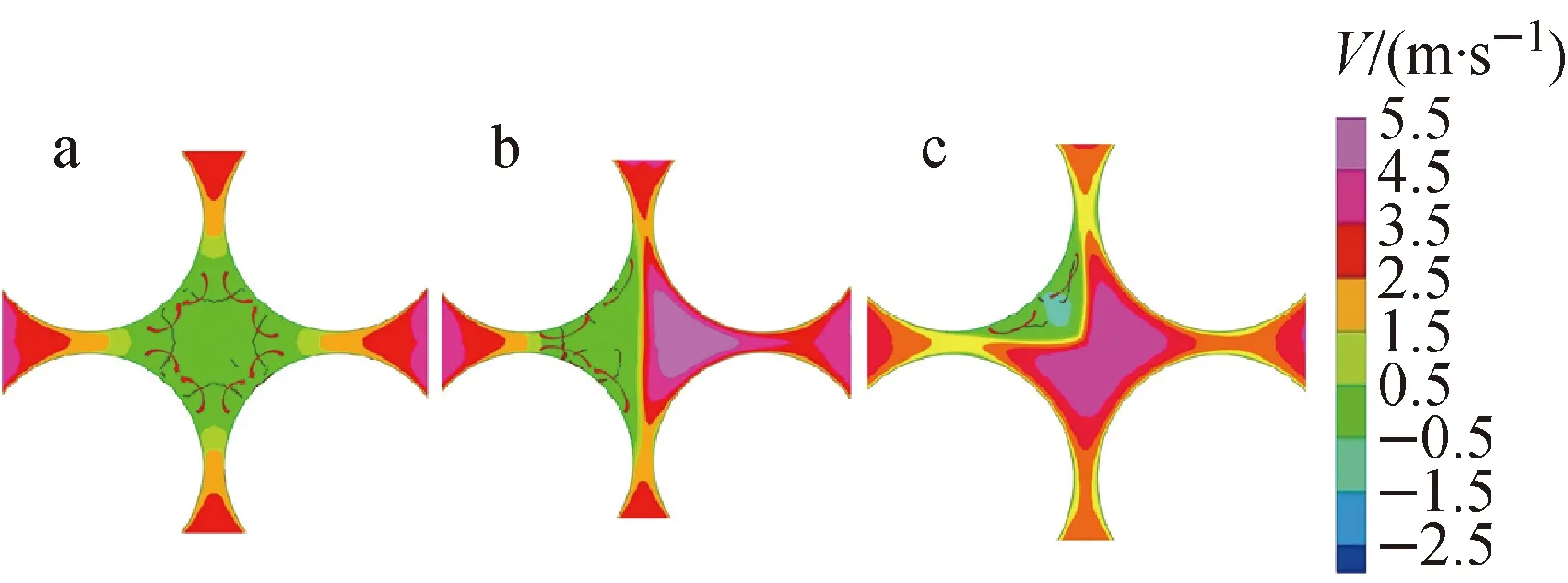
a——100%堵塞；b——50%堵塞；c——25%堵塞

Re=30 000下， 50%与25%堵塞率堵塞下游不同高度处子通道间隙的湍流交混系数对比示于图12，所检测子通道间隙位置均标识于图中。100%堵塞率工况计算结果如图8b所示。

对于50%堵塞率的情况：定性来看，堵塞物所在子通道间隙(G24、G25、G30)的湍流交混系数会有一明显的骤升现象，但G24、G25、G30的湍流交混系数变化行为又有所区别。G24的湍流交混系数呈快速下降，并未出现G25、G30湍流交混系数先增后减的现象，且衰减速度慢于G24。这是由于G25、G30附近有涡结构存在，而G24附近无大尺度涡结构导致的。G30的湍流交混系数增加量总体上小于G25，这是由堵塞物形状导致的，堵塞物占据G30的一半的同时占据了G25的全部，因此会对G25通道产生较G30通道更大的影响。对于堵塞物所在子通道相邻子通道间隙(G26、G41)，湍流交混系数在堵塞物下游约3Dh内快速下降至接近于正常工况。其余子通道间隙(如G49)的湍流交混系数增加并不明显。定量来看，堵塞物所在子通道间隙湍流交混系数最大会增至正常湍流交混系数的1.75倍左右，其相邻子通道湍流交混系数最大会增至正常工况的1.3倍左右，其余子通道增加幅度会更低。

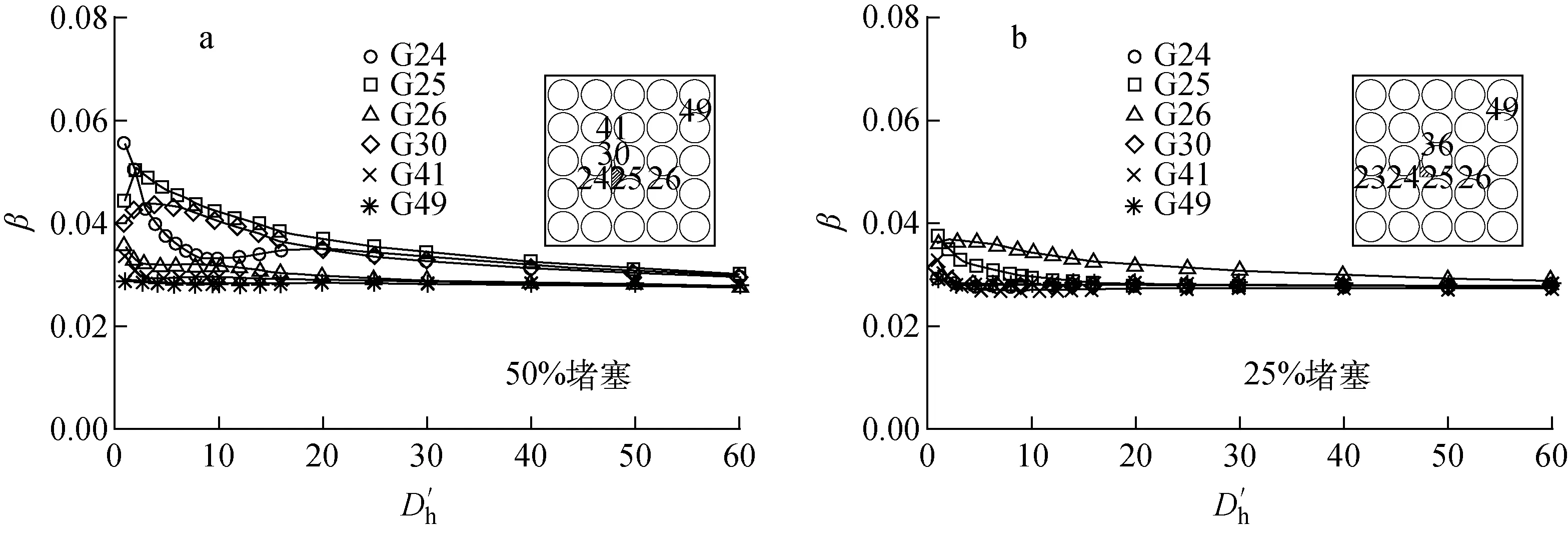
图12 边通道堵塞下游不同位置交混系数

对于25%堵塞率的情况：堵塞物所在子通道间隙(G24、G25)的湍流交混系数明显区别于其余子通道间隙，最大可增至正常工况的1.5倍左右。其中G24的湍流交混系数快速下降，G25的湍流交混系数受到涡结构的影响呈先增后减的现象，50%堵塞率时也有类似的现象，这说明附近存在涡结构的子通道间隙湍流交混系数会有波动，此波动表现为先增后减，且会较其余子通道间隙需要更长的距离恢复至正常工况。由于25%堵塞率较小，使得除堵塞物所在子通道以外的子通道间隙湍流交混系数在数量上相差很小，但同样存在堵塞物相邻子通道间隙湍流交混系数在约3Dh内快速下降的现象，而其余子通道变化幅度不明显。

综上分析，在堵塞下游，小的子通道堵塞率会减小堵塞给流场带来的扰动、降低下游的湍流交混系数峰值并有促进湍流交混系数恢复至正常工况的趋势。

2.4 不同堵塞长度交混程度对比

控制不同堵塞长度作为自变量，选取的堵塞子通道均为中心通道，对比了3种堵塞长度，即中心通道4 cm堵塞、中心通道2 cm堵塞、中心通道1 cm堵塞。

选取过渡流(Re=6 000)和湍流(Re=30 000)两流态工况下速度场结果进行分析，图13为两工况下中心通道堵塞段及其下游不同水力直径轴向速度云图。定性来看，对于堵塞对下游流场的纵向影响范围，堵塞长度的变化对堵塞下游流场恢复至正常工况所需的长度影响不大。从雷诺数的变化看，当流体处于湍流程度较强的湍流区时，堵塞长度较短会导致堵塞下游靠近堵塞段处流体流动情况更加复杂，这可能是由于堵塞段内流体在流道突缩后需要一定的长度使流体逐渐稳定，若堵塞长度较短，尚未稳定的流体即经突扩后进入堵塞下游，从而加剧了堵塞下游流动的复杂性。在此堵塞长度范围内，随着堵塞长度的改变，堵塞下游附近流体的当地雷诺数并无明显变化。

图13 不同堵塞长度下的流体速度云图

Re=30 000时不同堵塞长度堵塞下游涡核分布示于图14中红线区域。在堵塞长度4 cm工况，涡核分布较为对称；当堵塞长度为2 cm时，涡核分布的对称趋势有所减弱；当堵塞长度为1 cm时，涡核分布情况较为杂乱，且涡核存在的范围有所增加，除堵塞子通道内存在涡核，相邻子通道间隙附近亦有涡核出现，这是堵塞段内的涡尺度大于堵塞长度的结果。说明如果堵塞段长度较短，不足以使得堵塞段内流体的涡结构影响在堵塞段内完全消失，将导致堵塞下游流体行为更为复杂。

堵塞长度：a——4 cm；b——2 cm；c——1 cm

3种堵塞长度下，Re=30 000时G25、G36、G54的湍流交混系数对比如图15所示。对于G25，堵塞长度增大时，下游湍流交混系数的最大值亦会增加。当雷诺数较小时，3种堵塞长度的湍流交混系数恢复至正常工况的速度基本一致。当雷诺数较高时，低堵塞长度工况的湍流交混系数有较其余两堵塞长度下的湍流交混系数呈更明显的先增后减趋势，这是由湍流程度较高时低堵塞长度涡结构更为杂乱所致。对于G36，3种堵塞长度湍流交混系数的变化趋势相似，均为快速降低后逐渐趋于正常工况，说明低堵塞长度工况的涡结构对相邻子通道湍流交混程度的影响仍较小。对于G54，由于距离堵塞位置较远，3种堵塞长度的湍流交混系数基本一致。这反映不同的堵塞长度对堵塞段下游较近距离的湍流交混系数具有较大影响，但总体上不会影响湍流交混系数的恢复速度。

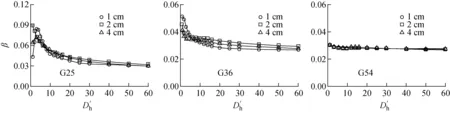
图15 不同堵塞长度下堵塞下游湍流交混系数对比

综上分析，当堵塞长度过短使得堵塞段内的涡尺度大于堵塞长度时，堵塞下游涡结构会较为复杂，导致流体的湍流交混系数会明显升高或产生波动；当堵塞长度足够包容堵塞段内的涡结构时，堵塞下游的涡结构会相对稳定。不同堵塞长度对堵塞下游较近位置流体的湍流交混系数影响较大，之后湍流交混系数会以相近的速度恢复至正常工况。

将3组不同堵塞条件的计算结果进行汇总分析，得出过渡区与湍流区堵塞下游不同子通道的湍流交混系数沿流动方向的变化规律，如表2所列。

3 结束语

本文采用实验与CFD数值模拟的方法对5×5紧密栅堵塞工况进行研究，获得了不同堵塞工况下通道内不同位置的湍流交混系数分布规律。分析表明：堵塞段及其下游存在的大尺度涡结构，是堵塞下游湍流交混系数复杂性的主要原因；定性来看，堵塞对不同位置流体的湍流交混系数存在一个主要影响范围，在堵塞子通道及其相邻子通道处，会明显区别于正常工况。对于其余子通道，湍流交混系数的变化很小，基本可忽略不计；定量来看，堵塞子通道下游湍流交混系数会增大至正常工况的3倍以内，并在15Dh内快速下降，之后逐渐恢复至正常工况，其余子通道下游湍流交混系数会增大至正常工况的1.5倍以内，并在6Dh内快速下降，之后逐渐恢复至正常工况。堵塞下游湍流交混系数相关结果可为子通道分析程序参数设置提供参考。

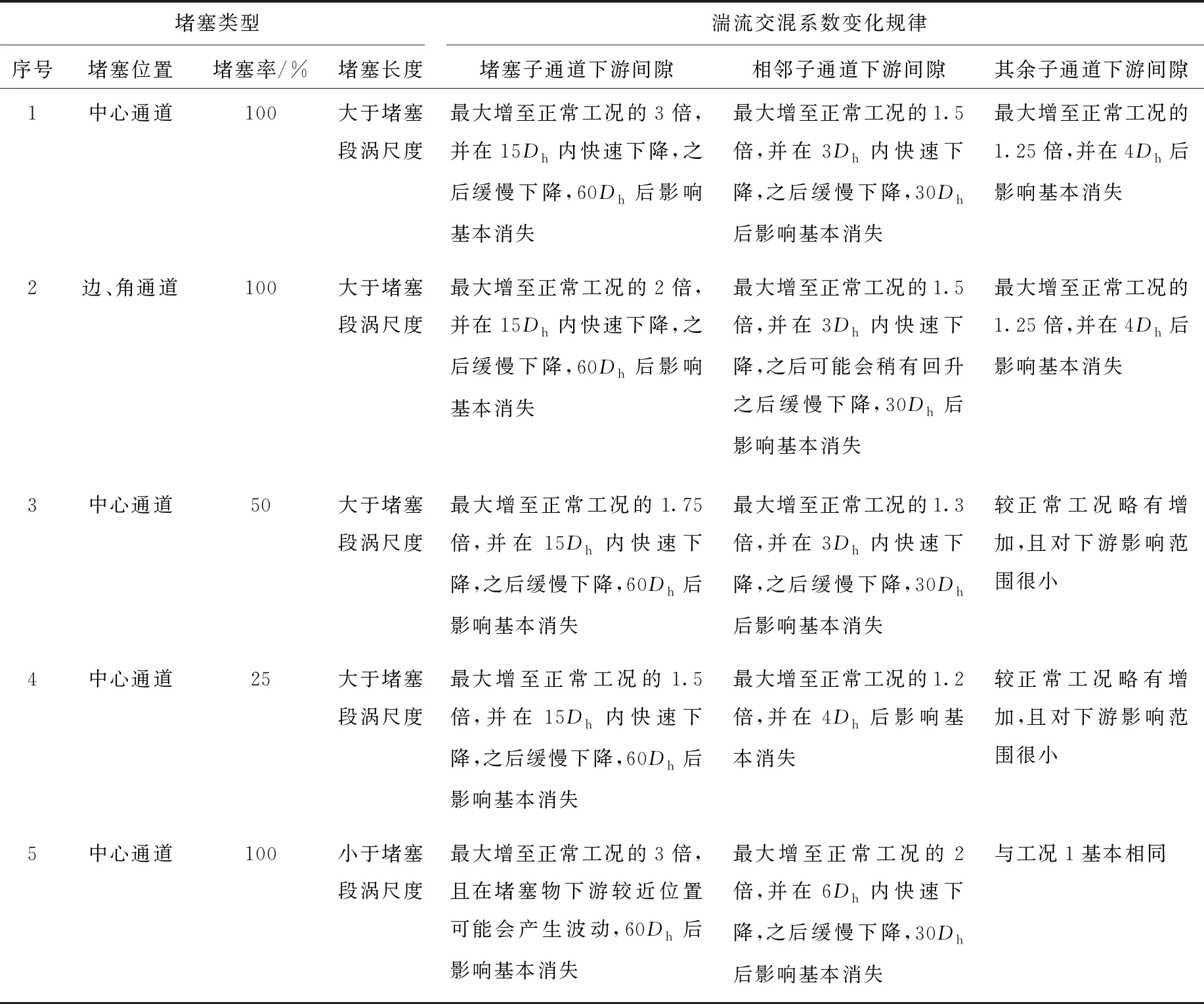
表2 堵塞下游湍流交混系数分布