基于水动力学方法的输水隧洞糙率反推及过水能力复核分析

沈国梁

(辽宁西北供水有限责任公司，沈阳 11003)

0 引 言

输水隧洞设计一项重要的参数即为糙率值，一般采用反推方法，结合试验方式对糙率值进行反演计算[1]。由于糙率值直接影响输水隧洞的过水能力，因此其对于隧洞设计质量而言，十分关键和必要[2]。理论糙率值需要结合实践进行验证，尤其是在输水隧洞设计完成后，亟需对其过水能力进行复核，复核输水隧洞断面的过水能力，是否满足输水量的要求[3-4]。针对输水隧洞过水能力复核的研究从20世纪已开始[5-10]，但这些方法由于很难采用原型观测的方式对输水隧洞内部流量进行测定，大都基于恒定流模型进行糙率的推算以及过水能力的复核。而输水隧洞水流由于受闸门起闭影响大都为非恒定流，采用恒定流模型很难对输水隧洞的糙率及过水能力进行准确复核。为此需要采用基于水动力学原理的方法来实现输水隧洞非恒定流的水流流态模拟，通过求解模型，实现隧洞糙率和断面过水能力的较为准确的复核。水动力学模型需要设置模型计算边界，这种边界一般为水位或者流量条件，需要采用原位观测方式进行水位和流量的测定，为此在具体试验过程中，采用一种流量水位一体化的监测仪器，在输水隧洞设置上下边界监测断面作为水动力学模型求解的边界条件。文章提出的方法可以为大型输水隧洞糙率反推和过水能力复核提供重要的参考。

1 模型构建

基于水动力学原理构建输水隧洞糙率糙率反推及过水能力复核模型，通过设置上下监测断面对模型的上下边界水位流量进行设置，模型能量平衡计算方程为：

(1)

式中：Q为断面流量，m3/s；Z为断面水位，m；A为过水断面面积，m2；x和μ为输水隧洞水平和横向方向距离，m；g为重力加速度，m3/s；t为时段计算步长，h；α为流速系数；Sf为水力学坡比，‰；B为断面水面宽度，m。文章采用Preissman四点加权差分方程对构建的水动力学模型进行求解，求解方程为：

(2)

式中：θ为加权系数；f为水位计算值，m和流量计算值，m3/s。

2 工程实例分析

2.1 试验断面布设

采用水动力学方法的关键在于上下边界的确定，文章上下边界为断面水位-流量关系，因此需要对上下游边界进行水位、流量的观测，试验中共设置5个断面，每个断面均进行水位、流量数据的测定，各断面之间的间距相同，均为100m。

2.2 水位-流量关系测定

流量的测定：主要采用SonTek-IQ底座型多普勒测流仪(见图1)进行测定，该仪器通过测定断面平均流速，再结合输水隧洞断面测定数据，对其过水流量进行测定。在输水隧洞中部底板区域进行仪器的安装，考虑防水作用在蓄电池安装在隧洞的顶部，将SonTek-IQ底座型多普勒测流仪和电池通过电缆进行连接，对电缆外部进行防护。为了降低泥沙淤积对流量测定的影响，在距离地面高度为10cm的位置放置流量监测仪器，采用U型钢板对仪器下部进行加固防护，此外为减低漂浮物对仪器影响，加长处理U型板的保护范围，对迎水侧进行密封处理。

图1 流量测定仪器

水位测定：各断面水位采用雷达水位计进行测定，考虑不同断面坡降的影响，采用悬挂方式对蓄电池和雷达水位计进行安装，雷达水位计和蓄电池均在隧洞顶部中间均与进行安装。隧洞底板距离雷达水位计之间的距离为2m, 仪器最大水深测定的范围为2.5m。

仪器参数设定：对水位和流量测定参数进行同步设置，一次测流时间设置为1min，每次测流的时间间隔为300s，在每小时内进行水位和流量自动观测的次数为15次，为了使得试验时间具有同步性，将流量和水位观测设置为统一时间。

2.3 水位-流量测定结果

通过对不同闸门开启高度下的水位-流量进行观测，不同断面在不同闸门开启高度下的水位和流量观测结果见表1和表2。

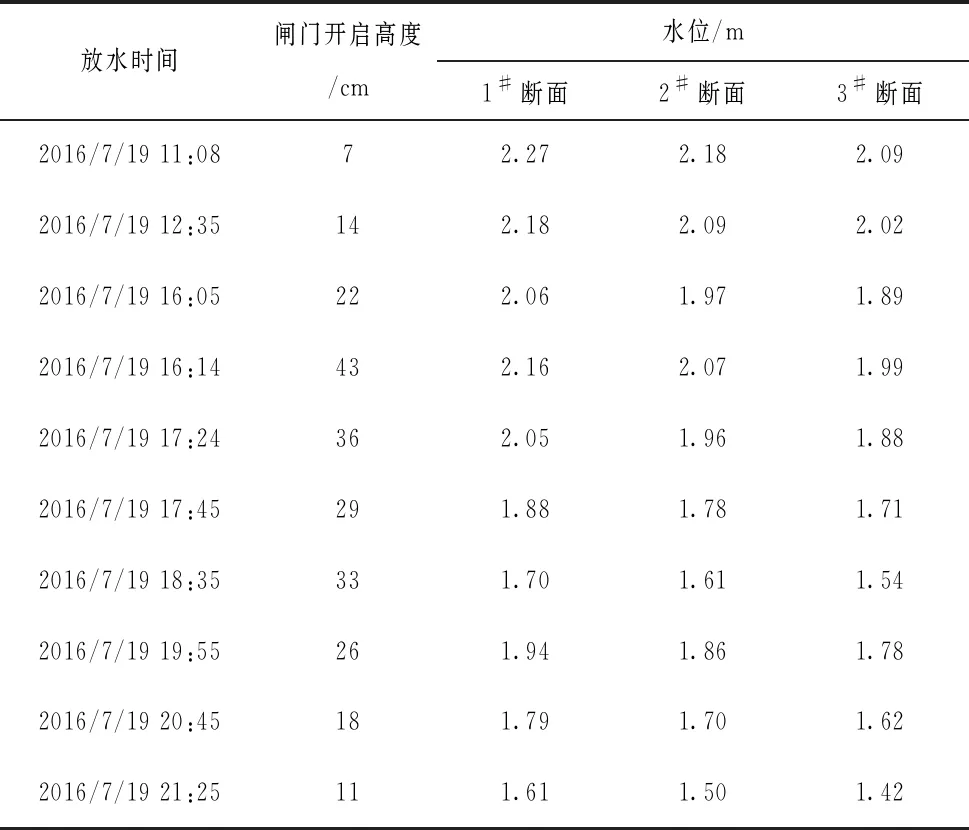
表1 不同断面水位测定结果

表2 不同断面流量测定结果

2.4 糙率反推计算结果

以1#和2#断面作为构建模型的输入上下边界的条件，采用试算方法对断面不同水深条件下糙率流量和水位进行计算。当采用的反推糙率计算的流量和水位和试验监测的同一个断面水位和流量较为相似时，则反推的糙率值符合精度要求。糙率计算结果如表3所示。

表3 输水隧洞糙率计算结果

从糙率反推值可看出，高水位条件下糙率反推的水位和流量与实测之间的拟合度要好于低水位条件下的拟合度，这主要是因为抬高了SonTek-IQ底座型多普勒测流仪的仪器安装高度，使得仪器的测流盲区减少，增加了仪器流量监测的范围。随着水深的不断提高，糙率反推的精度将不断提高，且糙率反推的水位、流量和实测水位、流量之间的吻合度逐步趋于稳定变化。此外从表中还可看出，因为输水隧洞考虑其设计的安全性，使得在同一水深条件下糙率反推值要低于糙率设计值。

2.5 合理性分析结果

为对糙率反推值进行合理性分析，结合3#监测断面实测流量测定结果，对糙率反推值进行合理性分析，分析结果见表4。

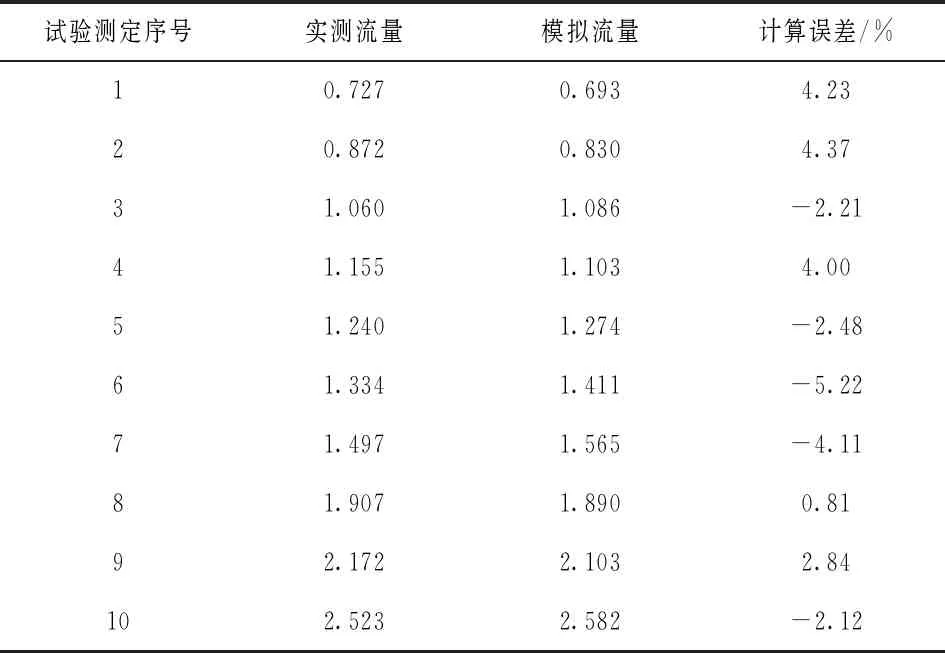
表4 输水隧洞糙率合理性分析

从合理性分析结果可看出，采用糙率反推的流量计算值好实测流量之间的误差低于10%，达到输水隧洞工程设计规范要求的误差允许范围要求。表明基于水动力学方法反推的糙率结果较为合理。这主要是因为输水隧洞由于闸门起闭原因，使得其水流流态为非恒定流，而水动力学模型可以较好的反映非恒定流的变化流态，相比于传统基于恒定流的计算方法，糙率反推计算结果更为合理。

3 输水隧洞过水能力复核

基于糙率反推值，对输水隧洞的断面过水能力进行复核，通过模型计算，当输水隧洞过水断面的水深达到1.8m时，经过复核输水隧洞的过水能力值为6.50m3/s，满足该输水隧洞设计过水能力的要求。

4 结 论

1)SonTek-IQ由于存在测流盲区，使得存在一定的流量测定误差，误差随着水深的增加有所改善，在水位较高时糙率反推的流量和水位和实测水位及流量之间的误差逐渐降低，且逐步趋于稳定变化。

2)水动力学方法可综合考虑输水隧洞非恒定流流态变化，相比于传统恒定流方法，其糙率反推精度更高，可解决传统方法糙率反推值精度不高的问题。