一种低复杂度的嵌入水印式物理层认证改进方案
2021-05-24吴聪,吴阳
吴 聪,吴 阳
(中国人民解放军陆军工程大学 通信工程学院,江苏 南京 210007)
0 引 言
由于无线通信的信号在开放空间中传播,因此无线通信的安全始终面临着严峻挑战。认证机制能够保证消息来源合法、内容完整且未被篡改,有效提高通信的安全性。根据认证目标的不同,认证可以分为2类,即身份认证和消息认证。通信系统中的接收机通过身份认证机制可验明接收信号的来源,确保接收信息的合法性,从而保证系统安全。传统的身份认证一般基于密码学原理,但这种认证机制存在缺陷[1]:(1)安全性难以保证。随着攻击者的计算能力不断提高和密码分析算法的进步,节点身份密钥被破解的难度大大降低。(2)频带利用率较低。基于密码学的认证机制需要额外的频带资源来传输认证信息,降低了频带利用率[2]。(3)不同设备采用的协议不同,认证方式难以兼容。
与传统认证方法不同,在物理层叠加身份认证信息不会影响上层的信息处理,不会占用额外的频带资源。有些物理层认证方案甚至无需解调信息即可完成认证,比如利用信道状态信息的物理层认证方案[3]。物理层认证可以极大降低认证时延和计算复杂度,提高认证效率。物理层认证作为补充加入原系统,可有效提高系统安全性。例如,利用星地信道特性可对GPS导航信号进行认证,有助于预防接收到恶意导航信号使船只偏离航线[4]。
物理层认证的身份信息有3种产生方式,分别为射频指纹、信道指纹和嵌入水印。射频指纹方法利用发射机固有的调制特性作为身份信息进行认证检测,接收机从接收到的信号中提取发射机的调制特征,与射频指纹数据库进行比对[5]。信道指纹方法与射频指纹方法类似,区别在于利用信道特征来认证。嵌入水印方法利用身份密钥生成认证标签,将认证标签叠加在信息信号中发送。其中,嵌入水印的物理层认证方法只改变信息信号功率,不会改动发送的信息内容,兼容性良好,且身份信息可控,可以实现大规模认证,相比另外两种方法具有一定优势。
目前嵌入水印的物理层认证方法得到了众多学者的关注。Paul等人将嵌入水印引入物理层认证用于身份认证,首次提出了嵌入水印认证方案[6]。以BPSK调制为例进行研究,理论上该方案可以推广到各种调制方法上使用。进一步,Paul等人提出了MIMO场景下的嵌入水印式物理层认证方案,并分析了系统的认证性能[7-8]。Xie等人更加详细地研究了Paul提出的水印认证方案,并采用一种新的度量—安全认证概率来统一衡量嵌入水印式物理层认证方案的性能[9]。之后,Xie等人还研究了NOMA场景[10]嵌入水印式物理层认证的具体方案。在提出的共享认证标签(PLA-SAT)、叠加独立认证标签(PLA-SIT)和时分复用认证标签(PLATDM)三种方案中,在NOMA场景下PLA-TDM方案最灵活,采用合适参数后认证性能最佳。根据Paul等人的研究,G.Verma等人使用USRP设备实现了嵌入水印认证方案,分别在QPSK和16QAM调制下完成了水印的叠加和检测[11]。采用BPSK调制时,信息和水印的调制信号只存在实数部分。采用硬件平台USRP做进一步的实验发现,接收端接收信号的实部和虚部两路信号可以分别进行处理,这为单独考虑信号实部进行物理层认证提供了现实依据。
1 系统模型和低复杂度的嵌入水印式物理层认证原理
1.1 系统模型
本文考虑一种典型的物理层认证模型[6],存在4种节点,即合法信号发射机Alice、合法接收机Bob和Carol以及攻击者Eve,Eve的主要攻击手段为窃听。其中,Bob和Carol的区别在于,Bob有检测认证标签的能力,而Carol没有,这意味着嵌入水印式物理层认证需要保证对认证方案不知情的合法用户也能在接收Alice消息信号时有不错的性能。部分研究文章[9]中用Carol用户的误码率来衡量认证机制的隐蔽性,本文暂不涉及。系统模型如图1所示。假设消息传输和认证过程中,无线信道经历平坦块衰落,信道衰落服从瑞利分布。同时,环境中存在加性高斯白噪声,噪声方差为。

图1 物理层认证系统模型
1.2 低复杂度的嵌入水印式物理层认证原理
低复杂度的嵌入水印式物理层认证方案中,根据合法发射机发送的信号是否叠加认证标签信号分为H0和H1,H0时发送的是不叠加标签的普通信号,H1时发送的是叠加标签的复合信号。标签信号由发送消息和共享密钥通过Hash函数加密再经过BPSK调制生成。发射机在2种情况下发射的信号为:

式中:ρs和ρt分别是合法收发端约定的信号幅度系数,满足;信息信号si和标签信号ti均为BPSK调制后的复向量,每个块均包含L个复数符号。因为采用BPSK调制,且原信息为随机的0、1 bit,所以消息和标签信号的每个元素均满足均值为0、方差为1的条件,且每个消息信号和其对应的标签信号不相关。因此无论是否叠加标签,发射信号总功率不变。
改进方案的接收端在接收到信号yi,Bob后,取出信号实部yi1,Bob,对其进行后续处理。假设接收端具有完美信道状态信息,对信号实部yi1,Bob做信道均衡,在H0和H1情况下,均衡恢复的信号分别为:

式中,hi1,Bob和ni1,Bob分别是瞬时信道和噪声的实部,ni1,Bob为L维矢量。
合法接收端在无差错解调出初始消息后,可以恢复原来经过调制的消息信号si。同时,根据消息和合法端共享的密钥,Bob使用相同方法可以重构可能叠加在发射信号中的标签信号,Bob端利用这些信息设计检测变量来判决发射机是否合法。根据标签信号的信号幅度系数ρt计算归一化的剩余信号:

将式(2)代入,可得剩余信号在H0和H1时分别为:

计算剩余信号和标签信号的内积,即两者的相干性,检测变量τi1,Bob在2种情况下分别为:

得到的检测变量与设定的判决阈值θ1进行比较,给出判定结果,是否认证通过。由于我们在接收到信号的第一步只取了实部的一路信号,所以此时检测变量τi1,Bob已为实数,无需再单独取实部。假设判决结果用φi表示,φi=0表示接收机对发射机本次的判决未通过,不存在标签;φi=1表示本次的判决通过,存在标签。Bob端判定结果可以表示为:

与本文方案不同,文献[9]中的认证方案未单独取实部来考虑,其检测变量τi,Bob与本文式(5)中的τi1,Bob的区别在于,文献[9]中与式(5)τi1,Bob项对应的vi,Bob在同时考虑信号实部和虚部时,应该表示为vi,Bob=(h*i,Bob/|hi,Bob|2)tiHni,Bob,其中hi,Bob和ni,Bob分别为完整的信道状态信息和噪声信号,为hi,Bob的共轭。因为信道服从瑞利分布,噪声为高斯白噪声,所以完整的信道状态信息hi,Bob~CN(0,σh2),噪声信号每个符号ni,Bob(l)~ CN(0,1),vi,Bob~CN(0,L/|hi,Bob|2)。
2 嵌入水印式物理层认证方案的性能与判决阈值选取
2.1 改进方案认证性能
嵌入水印式物理层认证在发送端叠加标签与否的情况下,通过标签的检测能力衡量方案的性能。根据是否叠加标签和是否成功检测分为4种情况,本文考虑其中的虚警和成功认证情况,进一步研究其错检概率。根据vi1,Bob的分布,可以推导出检测变量τi1,Bob在2种情况下不同的分布情况,分别为:

(1)虚警率:根据式(6)和式(7)可以求出发射机未叠加认证标签时,接收机错判为叠加了标签且通过了认证的概率,即虚警率,表示如下:


将zi,Bob的分布表达式代入式(8),Bob端的虚警率可以表示为:

(2)成功认证率:根据H1情况下τi1,Bob的分布,可以求出发射机叠加认证标签时,接收机成功检测并通过认证的概率PD,Bob:

使用随机变量zi,Bob进行计算,成功认证率可表示为:

(3)错检概率:假设H0和H1情况等概率发生,此时Bob端对是否叠加标签进行检测的错检概率为:
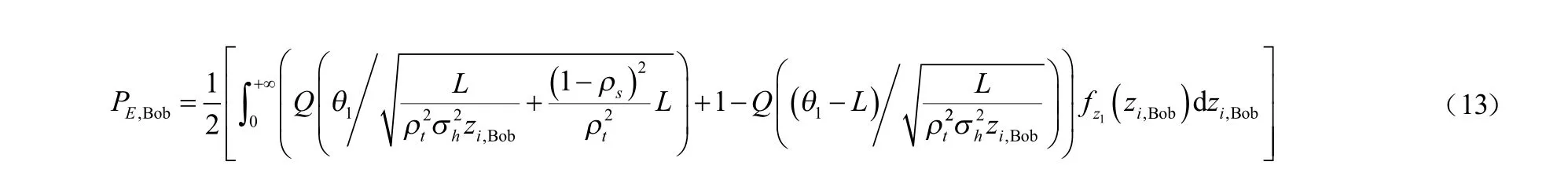
2.2 最佳判决阈值选取
为了降低错检概率,应选取合适的判决阈值θ1。只考虑实部的改进方案的检测变量和已有研究文献[12]存在差别,分布情况也不相同,因此文献中的最佳判决阈值不能继续使用。根据式(7),2种情况下的均值分别为0和L,因此,为区分这2种情况且使错检概率最低,最佳判决阈值θ*1应该在区间(0, L)中取值。PE,Bob的表达式对判决阈值θ1求一阶导和二阶导,通过计算可以发现,当θ1∈(0, L)时,二阶导P′′E,Bob始终大于0,所以一阶导P′E,Bob递增。进一步可以求出 P′E,Bob|θ1=0<0,P′E,Bob|θ1=L>0,所以 Bob 端的错检概率 PE,Bob在判决阈值θ1∈(0, L)时先减小后增大,存在最佳判决阈值使得PE,Bob最小,最佳阈值θ*1为P′E,Bob的零点。运用二分法可以得到最佳阈值的近似结果。
本文的物理层认证改进方案只考虑了信号的实部,除此之外,检测标签的流程和方法与文献[9]大致相同。在求出原方案的各项检测性能后,可以对判决阈值进行优化,以最小化错检概率。由于信号的虚部同样包含信息及信号能量,同时考虑实部和虚部的原方案能更准确地识别身份标签,但改进方案的优势在于计算复杂度更低,认证时延更短。
3 认证性能仿真分析与比较
3.1 原方案与改进方案认证性能比较
通过仿真分析,验证理论分析结果的正确性,并对低复杂度的嵌入水印式物理层认证方案的认证性能作定量评估。参考文献[9],设置仿真参数:设认证标签功率占比ρt2=0.1,每块的复数符号个数L=128。因假设噪声和信号的方差均为1,因此真实信道的方差σh2等于接收信噪比,仿真中信噪比取值为0~30 dB。采用1 000组随机信息和标签对,每组数据利用随机生成的瑞利信道和噪声传输1 000次,仿真1 000 000次。不同信噪比下Bob端采用改进的认证方案和原方案的仿真结果如图2所示。
从图2中可以看出,改进认证方案的仿真结果和理论推导吻合,虚警率、成功认证率和错检概率均满足预期。使用本文推导的改进认证方案最佳判决阈值时,Bob端的虚警率和漏检率近似相等,使得错检概率和虚警率近似。合法端Bob因为可以恢复标签信号,因此利用相干检测在信噪比很低的条件下实现较高的检测准确率。信噪比为25 dB时,改进方案的错检概率为0.009 892,低于0.01。但相比原方案,由于现在只选取了实部信号,因此存在部分信号能量的损失,体现在认证性能上时,表现为改进物理层认证方案的虚警率、成功认证率和错检概率比原方案差。总体而言,改进方案能够实现一定的认证功能。

图2 改进方案和原方案接收端性能仿真结果
使用改进的认证方案的突出优势在于计算复杂度低。以一次物理层认证标签检测中的信号均衡为例,原方案信号均衡的表达式为,当L=128时,计算需要4次实数乘法和1次实数加法。得到的复数再与128位信号复变量分别相乘,需要进行128次复数乘法,即512次实数乘法和256次实数加法,原方案在信道均衡时总计需进行516次实数乘法和257次实数加法。而改进方案信号均衡的表达式为,由于hi1,Bob和yi1,Bob分别为实数值和实数向量,因此改进方案在信道均衡时总计进行128次实数乘法即可。原方案和改进方案在接收信号后每一步的计算量对比见表1所列。从表1可以看出,使用改进方案可以减少一半以上的计算量。经计算可知,改进方案相较于原方案减少了55.709 3%的实数乘法和60.093 9%的实数加法,大大降低了嵌入水印式物理层认证计算复杂度,有利于进一步缩短认证时延。

表1 一次物理层认证标签检测所需运算量
表2给出了实际仿真结果,可以看出,改进的认证方案比原物理层认证方案的用时缩短约28%。尽管因为其他必要操作的存在,时延虽未缩短50%,但依然实现了很大的提升。

表2 两种方案时延比较
3.2 水印信号能量占比对改进方案认证性能的影响
根据式(10)、式(12)和式(13)可知,水印信号能量占比对改进方案的虚警率、成功认证率和错检概率性能均有影响,本文通过仿真实验定量分析水印信号能量占比对改进方案性能的影响。仿真设置与之前基本相同,取值为{0.01,0.02,0.05,0.1,0.2},每次仿真实验均选取相应的最佳判决阈值,不同取值时改进方案认证性能的仿真结果如图3所示。

图3 不同水印信号能量占比下改进方案认证性能
图3(a)~图3(c)分别为水印功率占比不同的情况下,改进方案合法接收端对标签信号进行检测的虚警率、成功认证率和错检概率。当信噪比从0~30 dB变化时,虚警率和错检概率逐渐趋近于0,而成功认证率逐渐接近1。随着认证标签信号能量占比提高,相同信噪比条件下虚警率逐渐降低,成功认证率逐渐升高,认证准确性逐渐提升,低信噪比时性能改善更为显著。这是因为提升标签信号能量占比可以在相同信噪比条件下提高标签信号能量,接收端进行相干检测时检测变量在H0和H1情况下的分布更加集中,正确区分2种情况的概率就越高。但由于发射信号的总功率不变,标签信号占用过高的功率会导致信息信号的功率过小。且在解调信息信号时,未知标签信号被当作干扰,过大功率的标签信号会导致解调时的信噪比低,从而可能导致差错率增大,需要设置额外的纠错措施,但此举会降低通信效率。
4 结 语
本文在采用BPSK调制的通信系统中提出一种低复杂度的嵌入水印式物理层认证改进方案,利用信号的实部对接收信号进行认证。和已有的物理层认证方案相比,在保证一定认证准确性的前提下,接收端信号处理的计算量减少了一半以上,大大缩短了认证时延。另外,研究发现,嵌入水印功率越大,认证性能越好。但水印功率会影响信息信号解调,因此需要选取合适的水印功率占比。
