基于MATLAB GUI的过程控制平台设计

宋莉莉 陈莉 马莉

摘要：针对“过程控制”中开出的实验项目难于理解、学习效果差等问题，利用MATLAB GUI开发相关实验项目的仿真平台，结合模块化思想，该仿真演示平台主要包括控制系统中数学模型分析方法的构建，如控制系统时域、频域、根轨迹以及稳定性分析等，并进行参数的设置，图形曲线的显示功能。最后通过设计弹出式菜单，可以对要实现的分析方法进行灵活选择。该平台操作方便，具有可扩展性，激发学生的学习兴趣，提高学生的动手能力和创新能力。

关键词：控制系统;平台设计;仿真;MATLAB GUI

中图分类号：TP3        文献标识码：A

文章编号：1009-3044（2021）11-0220-03

1引言

“过程控制”是自动化专业的主要课程之一，是在研究自动控制技术的基础课之上而开设的一门专业必修课程。该课程是集控制理论、工艺知识、自动化仪表与计算机为一体的综合性应用技术学科。针对在过程控制中对系统数学模型分析方法中所开设的实验具有计算量大，学生难于理解等问题，使得课程学习难度增加。为了解决这一问题，借助MATLAB 图形用户界面（Graphical User Interface，简称 GUI）GUI开发工具搭建可视化实验仿真平台尤为重要。

MATLAB是一种面向科学与工程计算的高级语言，用于高级技术计算语言和交互式环境，用于算法开发，数据可视化，数据分析和数值计算。广泛应用于各个领域，MATLAB已经成为研究和解决各种具体问题的软件。分析和设计可以增强控制理论的适用性。MATLAB软件中强大的可视化数据处理功能正好互补了控制理论学习中的局限性缺点。本文针对过程控制中对传递函数分析方法存在计算量大，公式推导烦琐，学生难于理解等问题，利用MATLAB GUI及控制系统工具箱，开发出基于控制理论的虚拟实验平台，利用本平台对其内容进行参数设置、仿真与研究。操作方便，激发学生学习兴趣。提供了学生的动手操作能力和创新能力。

2仿真演示平台构建

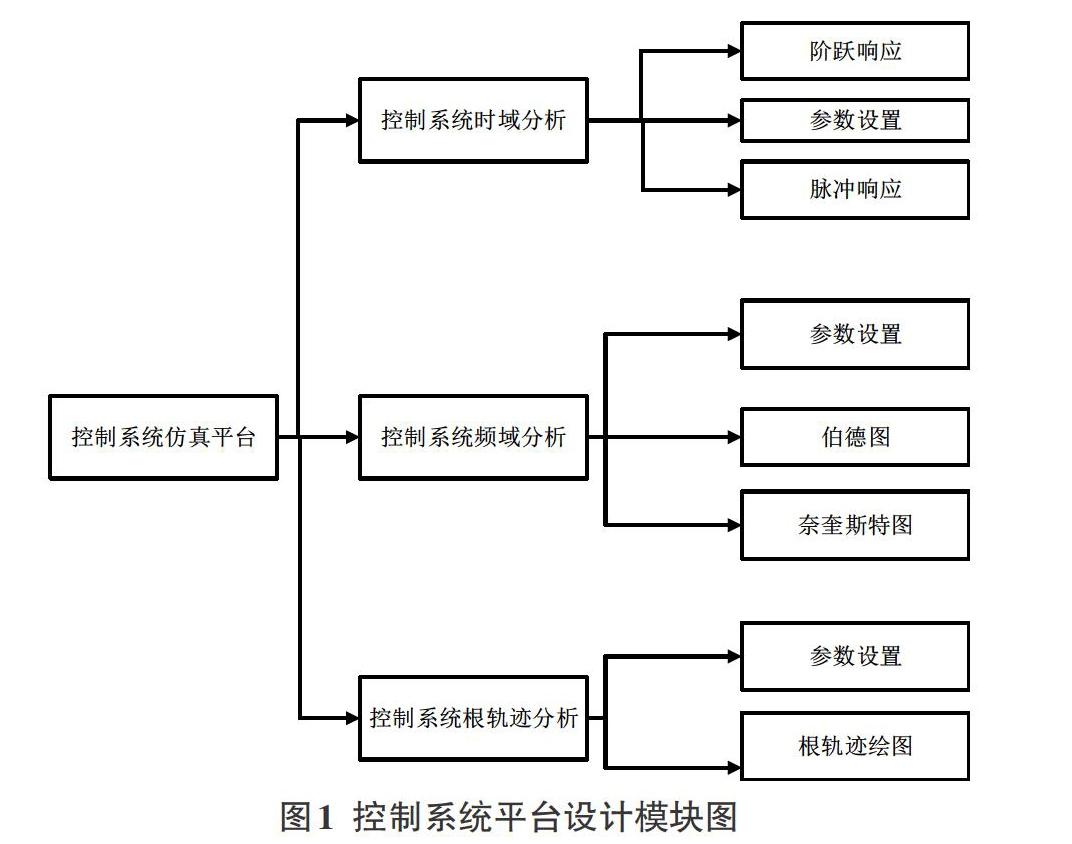
针对过程控制中的数学模型求解以及分析问题，为了更全面，更直观的理解数学模型分析，该仿真演示平台构建主要包括控制系统的时域分析、频域分析、根轨迹分析以及控制系统稳定性分析。其中时域分析又包含阶跃响应和脉冲响应，频域分析包括伯德图和奈奎斯特图的绘制。仿真演示平台主界面设计模块如图1所示。

GUIDE 是 MATLAB 图形用户接口开发环境，主要由窗口、光标、按钮、菜单、文本描述等组成。简化了设计和创建的过程。可完成 GUI 图形界面布局和 GUI 编程两项工作，对应扩展名分别为“[.fig]” 和“[.m]”。其中，“[.fig]”文件用来向界面中添加所需要的控件并设置其属性;“[.m]”文件通过 [Callback  ]回调函数实现控件操作中的相关功能。GUI是指由回调函数驱动的事件，回调函数主要是用于响应鼠标操作的用户界面控件。回调函数首先获得发出动作的对象句柄然后根据发出的动作，设置对象属性。[Callback]格式一般为：[function pushbutton1_Callback（h0bject，eventdata，handles）]。

其中，[hObject]：发生事件的控件;[eventdata]：保留字段;[handles]：当前对象句柄。按照GUI设计步骤，针对数学模型分析方法，设计如下图2所示的仿真演示平台。

3子系统的平台设计

3.1控制系统时域分析平台设计

时域分析是通过Largo的逆变换对特定输入信号的输出相应。在稳定控制系统中，对输入信号的时域响应分析包括两大部分：瞬态响应和稳态响应。分别描述系统的动态性能和稳态精度。对系统进行时域分析具有非常重要的意义。本文通过控制系统时域分析仿真平台的构建，主要分析了控制系统的阶跃响应和脉冲响应。首先建立一个新的GUI界面，在此界面上绘制两个静态文本并用鼠标双击静态文本在弹出的编辑器对话框中的“string”中的编辑框中写成“分子”和“分母给这两个静态文本框命名，引导用户在相应的可编辑文本中输入传递函数的分子和分母。为输入传递函数的分子分母分别绘制添加两个可编辑文本。再添加一个轴[axes]来画响应传递函数的曲线。最后添加阶跃响应和脉冲响应两个最重要的组件按钮，点击按钮将在坐标轴中画出曲线。以[Gs=s+12s2+s+5]为例，绘制系统阶跃响应，左键单击阶跃响应按钮选择查看回调点击Callback按钮，然后在

[function pushbutton2_Callback（hObject， eventdata， handles）]下输入程序：

[num=str2double（get（handles.edit1，'string'））;]

[den=str2double（get（handles.edit2，'string'））;]

[sys=tf（num，den）;]

[axes（handles.axes3）  %在坐标轴3下画图]

[step（num，den）]

[title（'阶跃响应'）;]

[xlabel（'时间'）;]

[ylabel（'振幅'）;]

[grid on  %有网格]

在输入框中输入分子：1 2;分母：215;接着点击“阶跃响应”按钮可得系统阶跃响应图如图3所示。

从图3可知，随时间推移系统逐渐趋于稳定。

3.2控制系统的频域分析

频率响应的方法是基于传递函数的另一种图型求解法。该方法可以根据系统的开环频率特性分析闭环系统响应 ，同時利用参数可分析对系统性能的影响，并提示改善的信息。

控制系统的频域分析平台主要包括伯德图和奈奎斯特图的绘制。在新的GUI界面，绘制两个静态文本分别为分子和分母，两个可编辑文本和一个伯德图按钮，一个奈奎斯特按钮。并设置属性。以传递函数[Gs=4s2+7s+13s2+s+5]为例，绘制奈奎斯特图，左键单击奈奎斯特图按钮选择查看回调点击[Callback]按钮，然后在[function pushbutton1_Callback（hObject， eventdata， handles）]下编辑程序：

[num=str2double（get（handles.edit1，'string'））;]

[den=str2double（get（handles.edit2，'string'））;]

[sys=tf（num，den）;]

[axes（handles.axes1）  %在坐标轴1下画图]

[nyquist（sys）]

[title（'奈奎斯特图'）;]

[xlabel（'频率'）;]

[ylabel（'对数尺度'）;]

[grid on  %有网格]

在分子和分母输入框中分别输入4，7，1和3，1，5。运行结果如图4所示。

由图4可知，传递函数在[s]右半平面没有任何极点即[P=0]，奈氏曲线不包括（-1，j0）点即[N=0]，根据[Z=P-N]，则[Z=0]，所以系统处于稳定。这与理论计算一致。

3.3控制系统的根轨迹分析平台

由于求解高阶特征方程式通常很困难，因此限制了系统分析在二阶系统以上的应用推广。1948年，W，R.Evans提出了一个根轨迹分析的方法，总结出自动控制系统的开环传递函数和闭环特征方程两者的联系，找寻闭环特征方程的根。由于该方法简单实用，因此适用于线性和连续系统以及线性固定系统并广泛应用于控制工程中，本文借助MATLAB仿真平台，构建根轨迹分析平台的子界面具体操作为首先打开新的GUI界面，绘制两个静态文本分子和分母，两个可编辑文本和一个绘图按钮并设置好它们的属性。以传递函数[Gs=s+22s2+5s+7]为例，分子输入1，2，分母输入2，5，7。点击绘图，结果如图5所示。

由图5可知，该系统有两个极点和一个零点。共有两条根轨迹，一条趋向于无穷远处，一条趋向于零点。该系统的所有根全部位于s平面的左半平面，因此系统稳定。这与理论计算一致。该平台可实现对控制系统数学模型根轨迹的绘制。

3.4控制系统的稳定性分析平台设计

分析控制的稳定性对控制系统基于非常重要的意义，只有系统稳定，才可以进一步的分析，由控制理论可知，传递函数的根都为负数时系统才会稳定。在MATLAB控制系统工具箱中，利用[eig（ ）]函数可以求取一个连续线性定常系统极点。来判别系统的是否稳定，另外，用图形的方式绘制出系统所有特征根或极点在[s]复平面上分布情况来判别系统的稳定性，当根全部分布在[s]的左半平面，则系统稳定。借助MATLAB GUI仿真工具，构建稳定性分析子界面。该界面主要包括两个静态文本分别为分子和分母，两个可编辑文本和一个分析按钮，一个零极点分布按钮。并设置属性。在分布按钮[function pushbutton3_Callback（hObject， eventdata， handles）]下输入程序：

[num=str2double（get（handles.edit1，'string'））]

[den=str2double（get（handles.edit2，'string'））]

[sys=tf（num，den）]

[p=eig（sys）]

[grid on;]

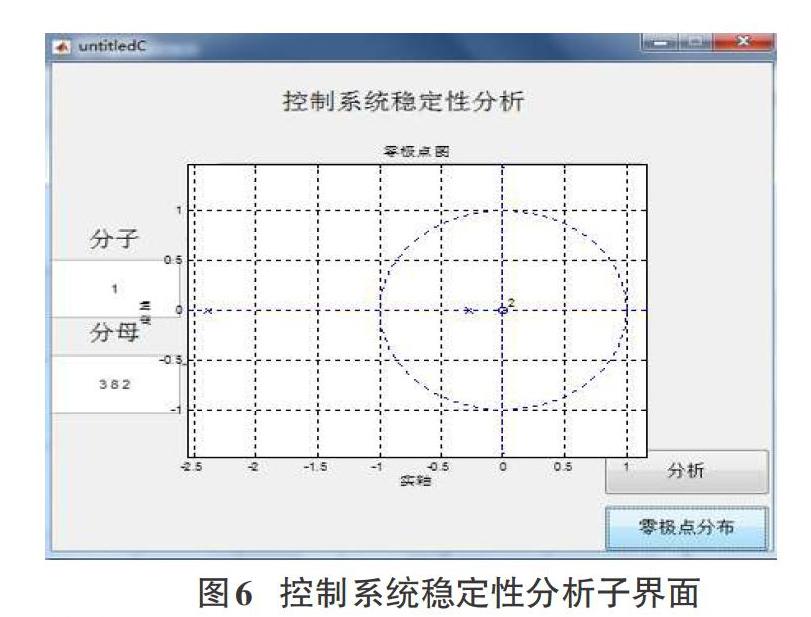
也可在分子框输入：1;分母框输入：3 8 2点击“分析”按钮，看其特征根是否均具有负实部，分析结果如下：[p1] =-2.3874，[p2=]-0.2792，均具有负实部，则系统稳定。点击零极点分布按钮，运行结果图图6所示。

从图6可以看出，该系统的零点和极点分布在[s]左半平面，则可判断系统稳定。可直观方便判别系统的稳定性。

3.5弹出式菜单设计

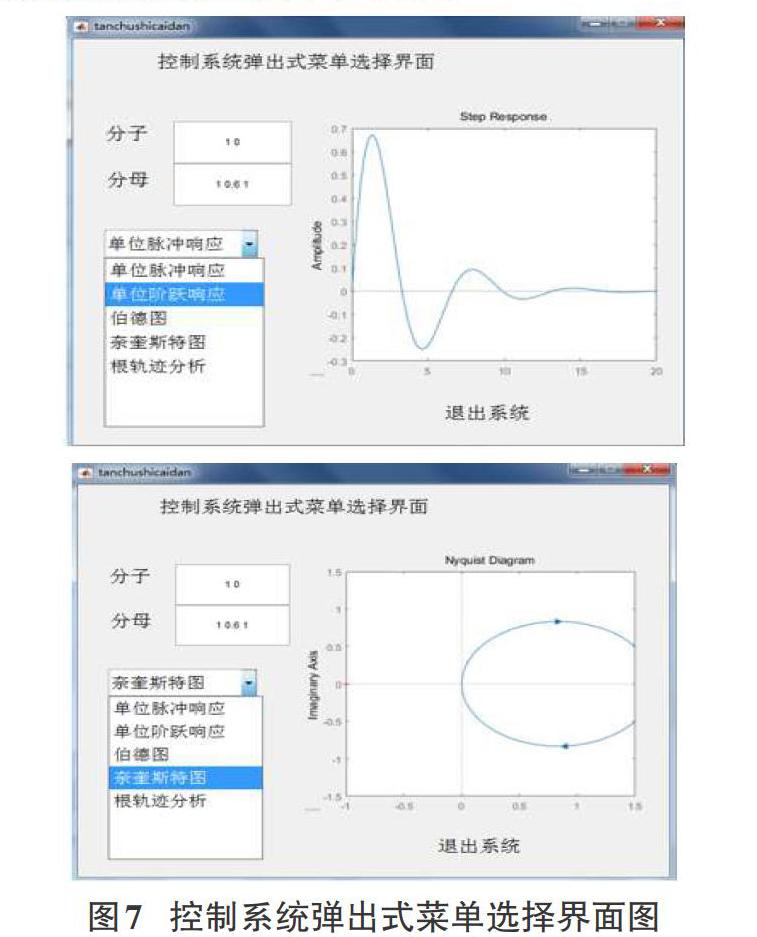
为方便学生灵活选择不同控制方法的仿真研究，提出在GUI中調用其他的GUI的方法完成切换不同分析方法的操作，使用GUI中弹出式菜单的按钮完成切换分析方法的操作。首先选择工具箱中“弹出式菜单”按钮添加在新建的GUI界面，选择在合适的位置。双击“弹出式菜单”按钮在弹出的检查器对话框中找到“[String]”这个选项填写入需要绘制的分析名称如阶跃响应，脉冲响应，伯德图，奈奎斯特图，根轨迹分析。以传递函数[Gs=ss2+0.6s+1]为例，分子：1;分母：1  0.6  1，分别将分子分母填入对应的静态文本里，点击弹出式菜单里对应的分析绘制的曲线将画在右边的坐标轴里。以单位阶跃响应和奈奎斯特为例，结果如下图7所示。

利用弹出式菜单可以灵活选择要分析的控制方法，激发了学生的兴趣，同时也可以提供学生的创新能力。

4结束语

针对过程控制的数学模型分析方法难于理解，计算量大，理论与实践脱节等问题，借助MATLAB GUI仿真软件，搭建控制系统的仿真演示平台，最后利用弹出式菜单灵活选择合适的 控制方法。不仅激发学生的学习兴趣，加深对理论知识的掌握和理解，从而应用于生产过程，更提高了学生的动手能力和创新能力，达到理论联系实际的目的，后续学习开发设计新型控制系统提供了基础。

参考文献

[1]  罗婷，聂俊飞，《MATLAB仿真技术》课程的非标准答案考试改革初探[J].邵阳学院电气工程学院学报，2018.

[2] 廖伶元，刘林，邱小平，等.MATLAB与相关学科交叉教学的改革与研究[J].价值工程，2015，34（31）：241-242.

[3] 张绍杰，刘春生.基于Matlab GUI的自动控制可视化仿真软件开发[J].电气电子教学学报，2018，40（6）：105-110.

[4] 王焕友，谭乔来.基于“信号与系统”的Matlab GUI实验仿真平台设计[J].电脑与信息技术，2019，27（3）：1-3，33.

[5] 陈梅，王健.基于MATLAB GUI的PID控制仿真系统设计[J].实验技术与管理，2020，37（2）：140-143.

[6] 闫洪波，王梦薇，等.基于Matlab GUI的医学图像处理仿真系统设计[J].计算机应用，2020（S1）：226-230.

[7] 苏小林，赵巧娥，MATLAB及其在电气工程中的应用[M].北京，机械工业出版社，2014.

【通联编辑：朱宝贵】