冗余双臂机器人协作空间分析与参数优化

胡平 林雪华 陈庆豪

摘要：以冗余双臂机器人为研究对象分析其协作空间，针对蒙特卡洛法算法不适用于冗余多自由度机器人，且存在计算速度较慢，求解的点云分布不理想等问题，对点云进行筛选后引入k近邻方法提取点云边缘，得出协作空间。仿真实验结果表明，工作空间边界点的提取效果较好，曲线拟合误差较小。为拟人机械臂的后续轨迹规划和运动控制奠定了基础。此外，也讨论了协作空间参数优化。

关键词：冗余双臂机器人;协作空间;蒙特卡洛方法;k近邻

中图分类号：TP183      文献标识码：A

文章编号：1009-3044（2021）11-0176-02

Collaboration Space Analysis and Parameter Optimization of Redundant Dual-arm Robot

HU Ping， LIN Xue-hua， CHEN Qing-hao

（Information and Engineering College， Jinhua Polytechnic， Jinhua 321007， China）

Abstract：Taking redundant dual-arm robots as the research object to analyze its collaboration space，then aiming at the problem that Monte Carlo method is not suitable for redundant multi-DOF robot， and the calculation speed is slow， and the point cloud distribution is not ideal， the k nearest neighbor method is introduced to extract the point cloud edge after the point cloud is filtered， and the cooperative space is obtained. The simulation results show that the extraction effect of boundary points in the workspace is better， and the curve fitting error is small. It lays the foundation for the follow-up trajectory planning and motion control of humanoid manipulator. In addition， collaborative space parameter optimization is also discussed.

Key words：redundant dual-arm robot;collaborative space;monte carlo method;KNN

雙臂机器人是目前智能机器人领域的研究热点，它结构与人类接近，在智能控制系统指挥下，可以通过双臂协作完成加工装配、生活服务甚至排除爆炸物品等灵巧复杂的任务，与单臂机器人相比具有更高的灵活性、操作性和负载能力。但与此同时，双臂机器人结构复杂，对其智能控制，特别是双臂协作等仍存在若干关键问题需要解决，如双臂机器人的协作空间问题就是此类机器人系统研究中的难点。

协作空间是双臂机器人的核心指标。它是指机器人双臂的末端执行器能共同到达的位置空间点集，是机器人双臂协作能力的重要体现。协作工作空间的研究，是进行机构设计、路径规划、轨迹规划和避障等的核心问题。尤其是在机器人的设计阶段和应用过程中，都应该对协作空间进行分析。

目前对机器人工作空间的研究在单臂机器人上成果较丰富，对双臂协作空间研究较少。求得工作空间的算法有3种：解析法、几何法和数值法，前两种方法不适用于双臂问题。数值方法精确度一般，但计算流程简单，结果直观，特别是利用随机采样，生成工作空间的数值类算法——蒙特卡洛法，从单臂机器人开始在工程应用中采用较多。荆学东、张清松和王威等研究人员[1-3]分析了双臂动力学模型，利用蒙特卡洛法求得了工作空间。

但是，蒙特卡洛法存在当自由度值升高后，计算用时长，得出点云分布不理想等问题。针对这一问题，本文在充分分析冗余双臂机器人的结构特征后，提出对蒙特卡洛法初步得到的点云进行筛选，再通过k近邻算法进行边界提取，从而确定协作空间，提升传统算法的计算速度和精度。

1 冗余双臂机器人的结构特征

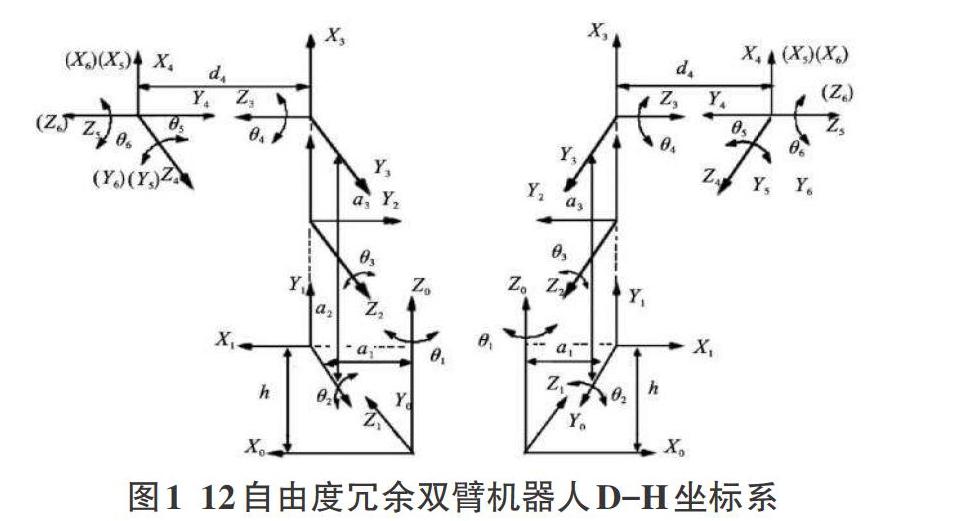
双臂机器人的每条机械臂与人体手臂结构类似，一般地由大臂、小臂和末端执行器（相当于人的手掌）等连杆组成，而肩部有3个自由度，大小臂连接处的肘部有1个自由度，腕部有2或3个自由度，即单臂为6或7自由度，整体为12或14自由度。本文腕部为2自由度。其D-H坐标系如图1所示。

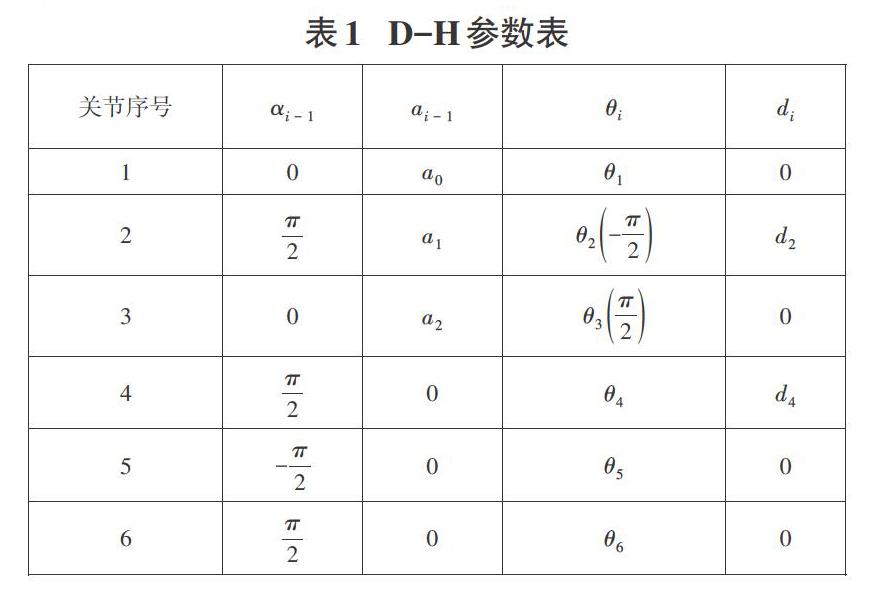
上图中[Xi，Yi，Zi]表示空间三维坐标，[ai]、[αi]、[di]和[θi]分别表示连杆长度、连杆转角、连杆偏距和关节角。结合机器人的物理结构限制和一般工作任务需求，本文拟定如表1所示某一臂D-H参数。

2 冗余双臂机器人的协作空间分析及求解

在理想条件下，双臂机器人的协作空间可以简单视为两条单臂的工作空间的交集。设[pi] 表示第[i] 条手臂的工作空间，[M]表示协作空间，则[M=p1?p2] ，[pi]可由下面的公式1得出。

[pi=xi=fixθi1，θi2，θi3xi，yi，ziyi=fiyθi1，θi2，θi3θimin≤θit≤θimaxzi=fizθi1，θi2，θi3-L]     （1）

其中，[t=1，2，3] 。

此时，一般方式是利用蒙特卡洛法通过设置大量随机值生成工作空间[pi]点云集合后进一步得出协作空间[4-5]，但本文研究对象自由度较高，直接生成的点云分布不理想，数据量大，导致求解的空间边界精度低，同时计算量巨大。

赵亚川等研究人员提出一种基于k近邻的算法，适用于冗余多自由度机械臂，仿真实验效果满足了工程要求，但其应用于特殊结构机器人。受文献[6]方法的启发，本文引入k-d树对蒙特卡洛法初步得到的点云进行筛选，再通过k近邻算法进行边界提取，从而确定协作空间，其核心步骤如下：

1）生成关节角[θi]随机值（随机数范围需大一些，如50万等），带入前文公式解出空间坐标，此时得到了较为粗糙的机械臂工作空间点云集合;

2）将步骤1的结果构造k-d树，将点云投影在2D平面上，在k-d树中筛选出与投影距离满足阈值要求的点;

3）基于k近邻算法对点云边界进行提取，最终确定协作空间。

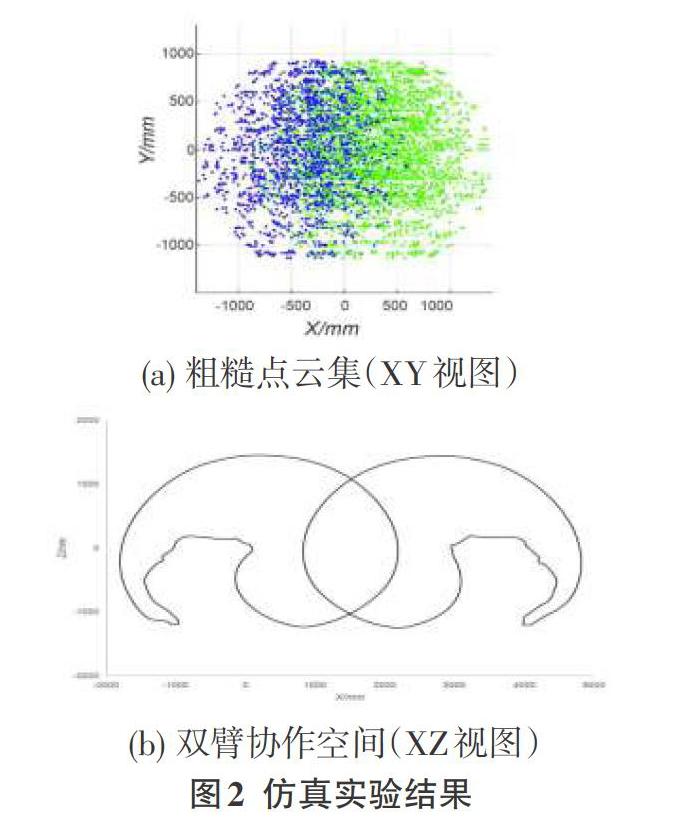
利用Matlab进行仿真实验，其初步得到的粗糙点云如图2（a）所示，最終提取到的协作空间如图2（b）所示。

3 协作空间参数优化分析

按照前文方法得出的协作空间并未考虑双臂机器人自碰撞等特殊情况，同时，在物理参数容许范围内，应该追求协作空间的最大化。针对这一问题，本文仿真实验时设定连杆长度[ai] 和关节角[θi] 在一定范围内取值，将求解的协作空间数量进行量化，通过遍历搜索求得最优化参数，实验结果反应[θ4]、[θ5]和[θ6]的取值范围变化对机器人协作空间影响较小，因此进一步优化了这些参数的取值范围，提升了算法效率。

4 结语

本文对服务机器人双臂协作空间进行分析，进一步对部分参数进行了优化。以冗余双臂机器人为研究对象，针对蒙特卡洛法在多自由度情况中运算慢、得出结果不精确等问题，借助k-d树筛选点云，再通过k近邻算法进行边界提取，确定协作空间后结合关节角取值范围，以协作空间最大为目标进行了一定优化。仿真实验结果验证了本文方法的可行性，同时也提升了传统算法的计算速度和精度，也为后续机器人的轨迹规划和双臂协调等问题的研究打下基础。

参考文献：

[1] 荆学东，薛毓铨，陈亚楠.6R双臂服务机器人协作空间分析及参数优化[J/OL].机械科学与技术：1-6[2020-11-03].

[2] 张清松，段帅臣，夏热.基于Matlab的拟人机械臂工作空间分析及仿真[J].机械传动，2020，44（12）：99-105.

[3] 王威，许勇，刘勇，等.基于Matlab的双机器人协作空间求解及分析[J].轻工学报，2019，34（4）：102-108.

[4] 李宪华，孙青，范凯杰，等.双臂6R服务机器人的协作空间分析与仿真[J].机械传动，2018，42（9）：130-134.

[5] 马小蒙，沈惠平，黄涛，等.冗余拟人双臂机器人的运动学及工作空间分析[J].机械设计，2014，31（11）：25-29.

[6] 赵亚川，李庆杰，高世卿，等.一种超冗余机械臂的工作空间求解方法[J].电子机械工程，2019，35（6）：61-64.

【通联编辑：唐一东】