基于扩张状态观测器的磁悬浮球的反步控制

李冰林 曾励 张鹏铭 竺志大

摘 要：针对单自由度磁悬浮系统的非线性、不确定性和易受扰动等特点，提出一种基于扩张状态观测器的反步控制方法以提高系统的控制性能。在系统受到不确定性扰动的情况下，运用扩张状态观测器实时估计悬浮球的位置、速度和扰动信息，并将这种估计值与控制器设计相结合，然后采用反步法设计磁悬浮球的悬浮位置跟踪控制律，以Lyapunov方法证明系统的跟踪误差最终有界收敛。仿真结果表明，ESO-BS控制与PID控制相比，前者系统调节时间为0.01 s，后者调节时间为0.08 s，明显偏长，因此，ESO-BS控制的动态特性要优于PID控制。在系统存在不确定性的条件下，所设计的控制律能实现磁悬浮球的稳定悬浮，并能根据要求的悬浮高度位置实现位置跟踪。

关键词：控制系统仿真技术;磁悬浮球;扩张状态观测器;反步控制;位置跟踪

中图分类号：TH117.1 文献标识码：A

doi：10.7535/hbkd.2021yx02007

Back-stepping control based on extended state observer for magnetic levitation ball

LI Binglin1，2，3，ZENG Li2，ZHANG Pengming3，ZHU Zhida2

（1.College of Automobile and Traffic Engineering，Nanjing Forestry University，Nanjing，Jiangsu 210037，China;2.College of Mechanical Engineering，Yangzhou University，Yangzhou，Jiangsu 225009，China; 3.Zhejiang Jinggong Science & Technology Company Limited，Shaoxing，Zhejiang 312030，China）

Abstract：Aiming at the characteristics of non-linearity，uncertainty and susceptibility to disturbance of single-degree-of-freedom magnetic levitation ball system，a back-stepping control method based on extended state observer （ESO-BS） was proposed to improve the control performance of the system.The extended state observer was used to estimate the position，velocity and disturbance information of the levitation ball in real time when the system was disturbed by uncertainty.The estimation was combined with the controller design，then the back-stepping method was used to design the levitation position tracking control law of the magnetic levitation ball，and the Lyapunov method was used to prove the ultimate bounded convergence of the tracking error of the system.The simulation results show that，compared with PID control，the adjusting time of ESO-BS control system is 0.01 s，while that of PID control is 0.08 s，which is obviously longer，so the dynamic characteristic of ESO-BS control is better than that of PID control.When there is uncertainty in the system，the designed control law can realize the stable suspension of the ball，and can realize the position tracking according to the required suspension height position.

Keywords：

control system simulation technology; magnetic levitation ball; extended state observer（ESO）; back-stepping control; position tracking

磁懸浮能使机械实现无摩擦、无需润滑高速运转，在交通、国防、工业等领域有较大的应用前景[1-2]。单自由度的悬浮系统具有非线性、开环不稳定的特性[3]，通常方法都是将系统在平衡点处线性化，然后再设计控制算法，如文献[4—5]采用的PID控制和模糊PID控制，尽管这些控制有一定的鲁棒性能，但容易使系统性能变得超调。考虑模型扰动的鲁棒控制虽然对模型的摄动有一定的容许度，但是该控制方法也需要合理选择灵敏度加权函数[6-7]。滑模控制响应快、对参数变化不敏感，但需要解决变结构时的抖振问题[8]。神经网络控制需对参数进行大量训练，对实时性和硬件要求较高[9-10]。以上控制都建立在悬浮球处在平衡位置小扰动下，一旦外扰强度增大，系统偏离平衡点的幅值过大，再由于系统非线性的因素，会导致系统失去稳定，进而悬浮失效。扩张状态观测器（ESO）将系统的内外干扰信号视为一种总扰动，并能通过观测器将这一总扰动进行估计，但在参数整定时比较复杂[11]。反步控制能够有效消除参数变化和外界扰动对系统的影响，可以处理不确定性以及带有未知参数的非线性系统，在四旋翼飞行器等控制领域有较为广泛的应用[12-13]。

本研究针对单自由度的悬浮系统，在外界存在扰动的情况下，采用扩张状态观测器取代对这种扰动进行估计，然后基于反步法设计磁悬浮球的位置控制器和移动速度控制器，抑制外界扰动，实现对磁悬浮球高度位置的精确悬浮控制，使得控制的位置误差最终有界。该方案不需要获取准确的线性化参数，同时不需要估计系统不确定项的上界，简化了系统控制，最后通过仿真验证该控制算法的可行性。

1 单自由度悬浮系统模型及问题描述

1.1 系统模型

1）悬浮球与电磁铁数学模型

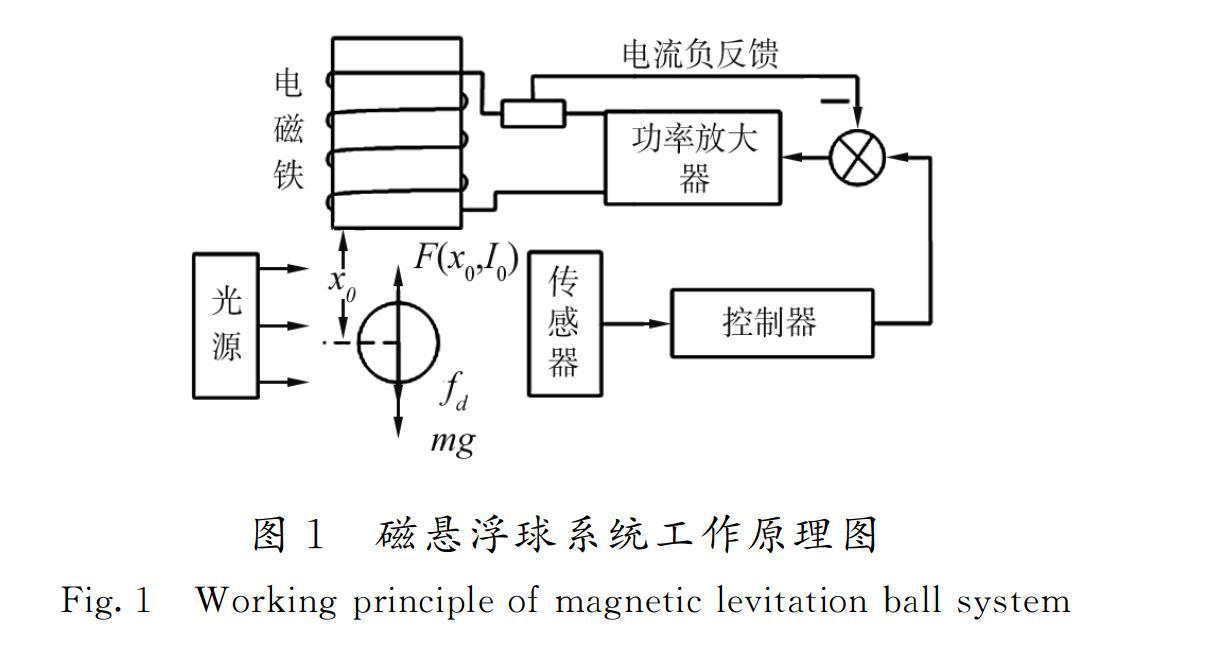
磁悬浮控制系统的工作原理如图1所示， F（x0，I0）是电磁铁在平衡点（I0，x0）处的电磁力，I0是线圈中的偏置电流。当系统工作时，悬浮球受到扰动，并从平衡位置x0向下偏移微小位移，经传感器检测，送入到控制器中。控制器紧接着向功率放大器输入控制信号，然后功率放大器将信号放大处理并向磁极线圈中输入电流为（I0+i），产生的电磁力将浮子拉回到平衡位置。

根据电磁学理论，忽略铁心的影响，悬浮球上的电磁力为[14]

F（x，I）=μ0S0（NI2x）2=14μ0n2S0I2x2=KI2x2，

式中：K=14μ0n2S0，电流I增加，电磁力增加;间隙x增加，电磁力减小。F（x，I）在平衡点（x0，I0）进行泰勒展开，电磁力等于悬浮球重力，即F（x0，I0）=mg，有：

F（x，I）=mg+μ0n2S0I0I-I0 2x20-μ0n2S0I20x-x0 2x30 。（1）

设工作过程中系统受到外力fd扰动，被悬浮对象的运动学方程为

md2xdt2=mg-F（x，I）+fd，

代入式（1），进一步得到：

md2xdt2+kxx+kII=fd，（2）

式中：k，kI分别为磁悬浮的位移刚度系数和电流刚度系数;kx=-μ0N2I20A/（2x30）;kI=μ0N2I20A/（2x20）。

令x1=x，x·1=x2，u=I，单自由度模型式（2）可表示为

x·1=x2，x·2=fd-kxxmx1-kIImu，（3）

式中：fd为外扰动;-kxxmx1视为内部扰动;f=fd-kxxmx1视为内外扰动之和。

2）传感器数学模型[15]

光电位置传感器具有线性特性，信号转换环节为电压放大器，属于比例环节，所以其模型可以简化为

Gs（s）=xs（s）x（s）≈Ks 。

3）功率放大器数学模型

采用电压-电流型功率放大器，其为一阶惯性环节，由于时间常数Ta极小，其数学模型可以简化为

G0（s）=i（s）u（s）=1+TasKa≈1Ka 。

由以上可知，模型中的传感器数学模型的输入、输出成线性关系，而功率放大器模型的输入、输出成反比例关系。

1.2 问题描述

在实际工作过程中，电磁线圈存在漏磁现象，铁心具有磁阻，存在磁饱和问题，这会增加系统的不确定性，同时外界的环境包括振动对系统控制都有一定的影响。这些问题都会导致系统建模存在偏差。为了降低这些因素对系统控制稳定性的影响，设计了一种扩张状态观测器对系统状态变量进行估计。

2 扩张状态观测器（ESO）

扩张状态观测器将系统未知的干扰信号扩充成新的状态变量，本文将f作为状态变量进行扩张。扩张状态器的输出动态补偿干扰项的影响，最终可将含有未知干扰项的系统用非线性反馈化为“积分串联”形式，然后用非线性状态误差反馈，设计理想的控制器[16-17]。

对于二阶非线性系统，可以表示为

x·=Ax+Bu+Ed，y=Cx，

式中：A=010001000〗;B=0b00〗;C=100〗;E=001〗T;d为扰动信息。

扩张状态观测器的增益为

z·=Az+Bu+L（y-y^），y=Cx，

式中：z=z1z2z3〗T，表示x=x1x2x3〗T的估计值;L=β01β02β03〗T，为观测增益。选择观测器的极点在左半平面-w0处，则：

sI-A=s3+β01s2+β02s+β03=（s+w0）3，（4）

得β01=3w0，β02=3w20，β01=w30，其中w0为观测器的带宽，满足多项式（4）是Hurwitz的，ESO能够收敛。观测器的输出z3将跟踪f。带宽的选择通常会考虑到信号的精度性和噪声的敏感性，应进行合理选择[18]。

扰动反馈控制律为

u=（u0-z3）/b0 ，

此时系统变为双积分系统。

传统的非线性反馈控制的控制增益：

u0=k1（v0-z1）+k1（v·0-z2） ，

式中：k1=w2c;k2=2wc，为控制增益;wc为系统带宽。

3 控制器设计

将扩张状态观测器的观测值与控制器设计相结合，以实现磁悬浮系统对干扰的抑制能力。反步控制器主要是基于Lyapunov稳定性理论[19]，实现对悬浮位置控制和速度控制。

Step1 根据式（3），希望找到一个x2d，使得t→SymboleB@，x1→x1d，根据扩展状态观测器的估计，即使z1→x1d，令：

e=x1d-z1 。（5）

对式（5）进行求导，则：

e·=x·1d-x·1=x·1d-x2 。

构造Lyapunov函数如下：

V1=12e2。（6）

对式（6）进行求導，则：

V·1=V1ededt=ee·=e（x·1d-x2）=-k1e2 k1>0，（7）

所以V·1<0，负定，因此，位移误差e逐渐趋近于0。

Step2 由式（7）可知，需使x·1d-x2=-k1e，重新令：

x2d=x·1d+k1e ，（8）

使得t→SymboleB@，x2→x2d，再令：

δ=x2d-x2，（9）

将式（9）代入式（7）得

V·1=e（x·1d-x2）=e·1d-（x2d-δ）〗，

将其代入式（8）得：

V·1=-k1e2+eδ 。

对式（9）进行微分，可得：

δ·=x·2d-x·2 。（10）

将式（3）、式（8）代入式（10）可得：

δ·=x··1d+k1e·-（fd-kxxmx1-kIImu）=x··1d+k1（x·1d-x2）-（fd-kxxmx1-kIImu） 。（11）

再構造Lyapunov函数如下：

V2=V1+12δ2。（12）

对式（12）进行微分，则：

V·2=V·1+δδ·=-k1e2+δ（e+δ·） 。

令：

e+δ·=-k2δ， k2>0 ，（13）

则：V·2=-（k1e2+k2δ2）<0，负定，因此，速度误差δ逐渐趋近于0。

Step3 求取控制律，将式（11）代入式（13）得：

e+x··1d+k1（x·1d-x2）-（fd-kxxmx1-kiimu）=-k2δ 。（14）

对式（14）进行整理，并同时根据扩张状态观测器对变量x1，x2的估计，可得控制律为

u=mkII··1d-k1（x·1d-z2）+（fd-kxxmz1）〗 。（15）

4 稳定性证明

将式（9）代入式（5）得：

e·=x·1d-x2=x·1d-（x2d-δ）=x·1d-（x·1d+k1e-δ）=-k1e+δ 。（16）

将式（15）代入式（10）得：

δ·=x··1d+k1（x·1d-x2）-fd+kxxmx1+kIImmkII··1d-k1（x·1d-x2）+（fd-kxxmx1）〗=-e-k2δ 。（17）

联立式（16）、式（17）得

e·δ·〗=-k1 1-1 -k2〗eδ〗 。（18）

设λ1，λ2为式（18）系数矩阵的特征值，则有：

λ1+λ2=-k1-k2，λ1λ2=k1k2+1。

由于k1，k2>0，可知λ1，λ2<0，系统渐进稳定。当t→SymboleB@时，e→0，δ→0。通过调节系统参数k1和k2可以改变所控制变量误差的收敛速度。

5 仿真试验分析

为了验证所设计控制器的效果，使悬浮球稳定地悬浮在离电磁线圈0.014 m的位置高度，在相同的初始条件下，仿真PID控制、Back-stepping（BS）控制以及基于扩张状态观测器的反步控制（ESO-BS）的控制效果，同时研究在悬浮位置的响应速度情况、抗扰能力以及跟踪性能控制参数。ESO中wc=200，w0=300，k1=700;k2=700;PID控制器的参数为kp=-0.45，ki=0，kd=-0.005，磁悬浮的结构和运行的具体参数值见表1[20]。

1）位置响应

图2为ESO-BS和PID 2种控制方法的悬浮位置阶跃响应曲线，悬浮球都能稳定地悬浮在0.014 m的位置处。由图2可知，ESO-BS的动态特性要优于PID控制，系统调节时间为0.01 s，PID控制的调节时间明显较长，为0.08 s，即对于单自由度的磁悬浮系统，ESO-BS控制在快速响应上得到了显著提高，远优于PID控制。

图3、图4为扩张状态观测器的观测值（z1，z2，f）与实际值的比较，可以看出，不论是观测出的位置信息、速度信息（位置的微分）、内外扰信息，两者之间的差值均很小，扩张状态观测器很好地跟踪到系统实际值、及微分信号和干扰信号。

2）抗扰控制

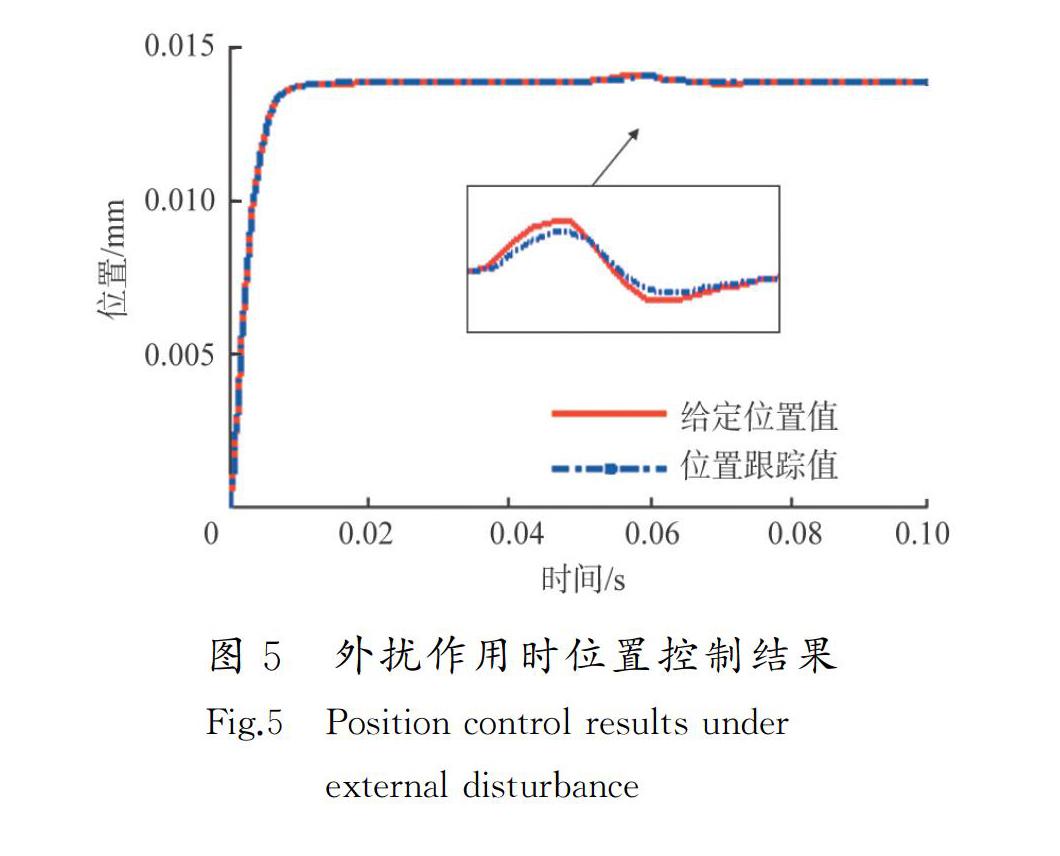
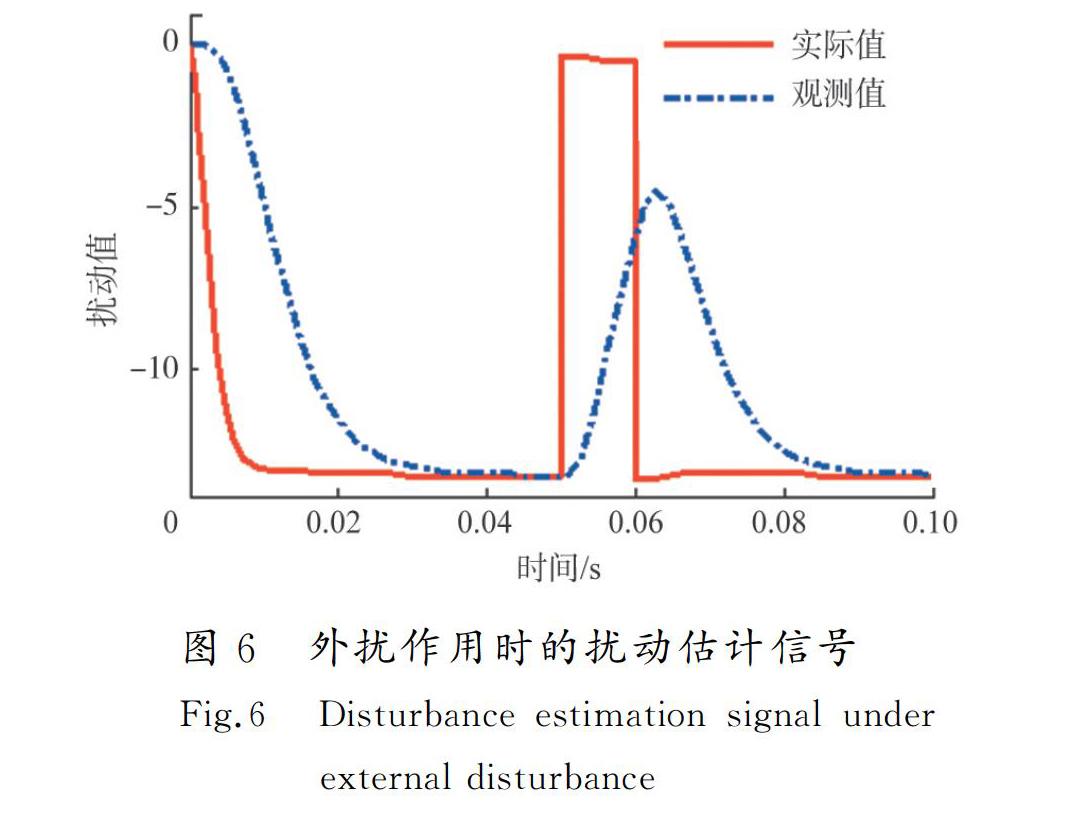
图5为在0.05～0.06 s时间段，施加扰动值13 N（为其自重的多倍），基于状态观测器的反步控制的控制效果。由图5可知，加入干扰后，磁悬浮球在加入扰动的时间段有微小波动，但最终仍维持在悬浮的0.014 m处。其他控制方式在加入同样大的负载后系统无法稳定。图6为扰动条件下扩张状态观测器的观测值（z1，z2，f）与实际值的比较，针对观测器输出的内外扰信息，估计值基本能跟踪到系统实际值。

3）跟踪控制

为了使磁悬浮球高度可调，使其跟踪所需要的悬浮高度，并验证控制算法的跟踪性能，令所跟踪的信号以0.014 m为基准高度，并对其施加振幅为0.01 m的正弦信号。

图7为扩张状态观测器输出的观测信号。由图7可知，控制系统可以使悬浮球及时跟踪输入参考量的变化，具有较好的跟踪性能，同时各个观测信号都表现出了较好的观测性能。速度跟踪方面，从初始阶段开始，实际速度值和观测速度值有很好的一致性，说明其有很好的跟踪性能，如图8所示。

6 结 语

针对悬浮球悬浮位置控制，设计了一种基于扩张状态观测器（ESO）的磁悬浮球的反步控制算法，通过观测ESO内外扰动信号，在Back-stepping控制器设计中以直接反馈的形式消除这种扰动，提高了系统的抗干扰能力。在位置响应控制中，该方法比PID控制调节时间短，响应快;在抗扰控制中，针对外界施加的扰动力矩，能对扰动进行估计，使悬浮球稳定悬浮;跟踪性能方面，能使磁悬浮球稳定跟踪给定位置信号。因此，该算法具有较好的控制性能。

本文算法的效果主要体现在软件仿真上，未来需在具体实物平台上进行实验验证。

参考文献/References：

[1] LEE H W，KIM K C，LEE J.Review of maglev train technologies[J].IEEE Transactions on Magnetics，2006，42（7）：1917-1925.

[2] 周天豪，陈磊，祝长生，等.基于自适应变步长最小均方算法的磁悬浮高速电机不平衡补偿[J].电工技术学报，2020，35（9）：1900-1911.

ZHOU Tianhao，CHEN Lei，ZHU Changsheng，et al.Unbalance compensation for magnetically levitated high-speed motors based on adaptive variable step size least mean square algorithm[J].Transactions of China Electrotechnical Society，2020，35（9）：1900-1911.

[3] 呂治国，龙志强.磁悬浮球系统的非线性自适应控制方法[J].控制工程，2020，27（1）：127-133.

LU Zhiguo，LONG Zhiqiang.Method on nonlinear adaptive controller for maglev levitation ball system[J].Control Engineering of China，2020，27（1）：127-133.

[4] 邱洪，黄苏丹，曹广忠.基于DSP的磁悬浮球模糊PID数字控制器[J].武汉理工大学学报（信息与管理工程版），2009，31（6）：933-936.

QIU Hong，HUANG Sudan，CAO Guangzhong.Development of fuzzy PID controller for magnetic levitated ball system based on DSP[J].Journal of Wuhan University of Technology （Information & Management Engineering），2009，31（6）：933-936.

[5] SUMAN D，BHATT R.Robust I-fuzzy controller for magnetic ball levitation[C]//2017 International conference of Electronics，Communication and Aerospace Technology （ICECA）.Coimbatore：[s.n.]，2017：618-621.

[6] 李群明，朱伶，徐震.磁悬浮球的鲁棒控制器设计[J].中南大学学报（自然科学版），2007，38（5）：922-927.

LI Qunming，ZHU Ling，XU Zhen.Robust controller design of maglev ball system[J].Journal of Central South University （Science and Technology），2007，38（5）：922-927.

[7] 黎恒，肖伸平.磁悬浮球系统的滑模变结构鲁棒控制器设计[J].湖南工业大学学报，2014，28（1）：58-61.

LI Heng，XIAO Shenping.Design of sliding mode variable structure robust controller for magnetic levitation ball system[J].Journal of Hunan University of Technology，2014，28（1）：58-61.

[8] 张井岗，方线伟，赵志诚.磁悬浮球系统的分数阶滑模控制[J].南京理工大学学报（自然科学版），2014，38（1）：72-77.

ZHANG Jinggang，FANG Xianwei，ZHAO Zhicheng.Fractional order sliding mode control of magnetic levitation ball system[J].Journal of Nanjing University of Science and Technology，2014，38（1）：72-77.

[9] CHIJINDU A T，ANGELA U E.Improving the intelligent control of magnetic levitiation ball using artificial neural network[J].International Journal of Engineering and Computer Science，2019，8（6）：24679-24685.

[10]沈昕璐，莫鑫，周亚南.基于模糊神经网络的磁悬浮球位置控制研究[J].农业装备与车辆工程，2018，56（5）：59-64.

SHEN Xinlu，MO Xin，ZHOU Yanan.Magnetic levitation ball position control research based on fuzzy neural network[J].Agricultural Equipment & Vehicle Engineering，2018，56（5）：59-64.

[11]张鋆豪，张文安.磁悬浮球系统的线性自抗扰控制与参数整定[J].系统科学与数学，2017，37（8）：1741-1756.

ZHANG Junhao，ZHANG Wenan.Linear active disturbance rejection control to magnetic levitation ball system and parameters tuning[J].Journal of Systems Science and Mathematical Sciences，2017，37（8）：1741-1756.

[12]姚达琛，堵威，唐漾.基于扩张状态观测器的四旋翼积分滑模反步控制[J].东华大学学报（自然科学版），2020，46（2）：260-268.

YAO Dachen，DU Wei，TANG Yang.Backstepping controller based on integral sliding mode controller for quadrotor with extended state observer[J].Journal of Donghua University（Natural Science），2020，46（2）：260-268.

[13]费爱玲，李柠，李少远.固定翼无人机的自抗扰反步控制[J].控制理论与应用，2016，33（10）：1296-1302.

FEI Ailing，LI Ning，LI Shaoyuan.Active disturbance rejection back-stepping control of fixed-wing unmanned aerial vehicle[J].Control Theory and Applications，2016，33（10）：1296-1302.

[14]王晓乐.磁悬浮球系统控制算法的研究[D].成都：西南交通大学，2016.

WANG Xiaole.Research of Control Algorithm of Magnetic Levitation Ball Control System[D].Chengdu：Southwest Jiaotong University，2016.

[15]钱玉恒，杨亚非，张翔.离散滑模变结构控制在磁悬浮球系统中的应用[J].中国惯性技术学报，2012，20（3）：368-372.

QIAN Yuheng，YANG Yafei，ZHANG Xiang.Application of discrete sliding mode variable structure control in magnetic levitation ball system[J].Journal of Chinese Inertial Technology，2012，20（3）：368-372.

[16]HUA X X，HUANG D R，GUO S H.Extended state observer based on ADRC of linear system with incipient fault[J].International Journal of Control，Automation and Systems，2020，18（6）：1425-1434.

[17]夏先齐，张葆，李贤涛，等.基于扩张状态观测器的永磁同步电机低速滑模控制[J].光学精密工程，2019，27（12）：2628-2638.

XIA Xianqi，ZHANG Bao，LI Xiantao，et al.Low speed sliding mode control of permanent magnet synchronous motor based on extended state observer[J].Optics and Precision Engineering，2019，27（12）：2628-2638.

[18]TIAN G，GAO Z.Frequency response analysis of active disturbance rejection based control system[C]// IEEE International Conference on Control Applications.[S.l.]：IEEE，2007：1595-1599.

[19]黃书童，江驹，李欧迅，等.近空间可变翼飞行器小翼切换滑模反步控制[J].飞行力学，2020，38（2）：29-33.

HUANG Shutong，JIANG Ju，LI Ouxun，et al.Sliding mode backstepping control for near space morphing vehicle winglet switching[J].Flight Dynamics，2020，38（2）：29-33.

[20]曹广忠，潘剑飞，黄苏丹，等.磁悬浮控制系统控制算法及实现[M].北京：清华大学出版社，2013.