考虑充电需求和时间窗的多AGV调度优化建模

陈香玲 郭鹏 温昆 裴霞

摘 要：为了提高自动引导小车 （automatic guided vehicle，AGV）在物流分拣中心的分拣效率，考虑采用纯电力驱动的AGV分拣过程存在电量消耗和充电需求的特性，提出了一种优化模型。在考虑AGV剩余电量和包裹时间窗等约束条件的基础上，建立了以最小化分拣作业周期为目标的混合整数规划（MIP）模型并提出了相应的约束规划（CP）模型，模型中使用区间变量表示任务的执行情况，借助累积函数记录电量的变化情况。计算结果表明，与MIP模型相比，CP模型拥有更好的求解性能。采用混合整数规划与约束规划构建AGV调度模型，可以有效提高分拣效率，降低企业运营成本，并为考虑更多约束的AGV调度研究提供求解途径。

关键词：物流系统管理;多AGV调度;充电需求;时间窗;约束规划

中图分类号：F252.1; TP23 文献标识码：A

doi：10.7535/hbkd.2021yx02001

收稿日期：2020-12-28;修回日期：2021-03-01;责任编辑：冯 民

基金项目：國家自然科学基金（51405403）;国家重点研发计划项目（2020YFB1712200）

第一作者简介：陈香玲（1996-），女，四川达州人，硕士研究生，主要从事运筹优化方面的研究。

通讯作者：郭 鹏副教授。E-mail：pengguo318@swjtu.edu.cn

陈香玲，郭鹏，温昆，等.考虑充电需求和时间窗的多AGV调度优化建模.河北科技大学学报，2021，42（2）：91-100.

CHEN Xiangling，GUO Peng，WEN Kun，et al.Optimized mathematical models for multi-AGV scheduling problem with charging requirements and time windows.Journal of Hebei University of Science and Technology，2021，42（2）：91-100.

Optimized mathematical models for multi-AGV scheduling problem with charging requirements and time windows

CHEN Xiangling1，2，GUO Peng1，2，WEN Kun1，2，PEI Xia1，2

（1.School of Mechanical Engineering， Southwest Jiaotong University， Chengdu，Sichuan 610031， China; 2.Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province， Chengdu， Sichuan 610031， China）

Abstract：In order to improve the sorting efficiency of automatic guided vehicle （AGV） in the logistics sorting center， an optimized model was proposed considering the characteristics of power consumption and charging demand in the sorting process of electric-driven AGVs. On the basis of considering of the AGVs remaining power and package delivery time window， a mixed integer programming （MIP） model with the minimization of the sorting operation cycle and a corresponding constrained programming （CP） model were formulated. In CP model， the interval variables were used to describe the performance of tasks and the change of electric quantity was recorded by using cumulative function. The computational results show that the CP model has better performance compared with the MIP model.Adopting mixed integer programming and constrained programming to formulate the AGV scheduling model can effectively improve the sorting efficiency，reduce the operating cost of enterprises， and provide an alternative solution for the AGV scheduling problem with more constraints.

Keywords：

logistics system management; multi-AGV scheduling; charging demand; time window; constrained programming

近年来，随着各大电商的高速发展，包裹数量逐年增多，物流分拣中心对分拣解决方案的高效率和高柔性提出了更高要求。目前，电商物流分拣中心主要采用大型交叉带分拣机和人机结合的模式[1]，虽具有较高的物流分拣效率，但是交叉带分拣设备的大型化决定了分拣中心场地的大型化，极大制约了中小型物流分拣中心建设的推广。小包裹、小型化的物流分拣应用场景越来越广，传统的大型分拣设备难以适应当前物流公司小型化分拣的需求。在此背景下，AGV作为自动化现代物流设备兼具柔性、效率和成本优势，在物流分拣中心得到了越来越广泛的应用[2]。因此，如何提高多AGV调度的效率也逐渐成为研究热点[3]。

虽然目前已有许多关于AGV调度的研究，但大多集中在制造[4]领域，特别是在柔性制造系统中的车间调度领域[5-7]。在物流分拣行业，多AGV调度问题的研究仍是一个新的趋势。BOYSEN等[8]研究了一种特殊的基于零件到取料机仓库的拣选订单处理系统。为了提高自动化分拣仓库中的分拣效率，袁瑞萍等[9]设计了改进共同进化遗传算法;贺学成等[10]针对高密集度的AGV分拣场景，提出了可避免拥堵的CAA*算法;XING等[11]提出了一种新的禁忌搜索算法，该算法可以解决多辆AGV同时工作时可能产生的冲突问题;余娜娜等[12]综合考虑了AGV调度和路径规划问题，设计了一种改进差分进化算法。

在以上多AGV调度研究中，AGV的电量消耗和充电需求始终是一个被忽略的问题，且现有的国内外研究大多集中在传统的调度问题，很少考虑充电需求。为了验证考虑充电需求的必要性，MCHANEY[13]通过数值实验验证了各种电池使用方案对AGV的数量规划、作业时间和调度优化等方面的影响，提出若AGV为纯电力驱动，则需要在实际作业中考虑其充电需求。随后，一些研究开始增加AGV电量作为调度考虑的约束，但没有考虑为AGV安排充电任务，部分研究中虽然存在电量限制，但只是使系统中的AGV在电量不足时无法参与后续任务[14-16]。近年来，周小凡等[17]研究了考虑AGV充电任务和充电等待时间的集装箱码头多AGV调度问题，并建立了数学模型。张亚琦等[18]考虑了垂岸式集装箱堆场布局和AGV 充电过程对实际作业的影响，并设计了遗传算法。LIU等[19]将AGV的充电任务纳入到任务调度优化中，提出了无人仓库中多AGV调度的多目标数学模型，开发并集成了2种自适应遗传算法（AGA）和多自适应遗传算法（MAGA）。

基于以上分析发现，现有的研究大多忽略了AGV电量消耗这一现实因素，少数文献考虑了电量消耗问题，但没有考虑执行充电任务对实际工作的影响。本文结合实际情况，不仅考虑了AGV的充电需求，还进一步加入了包裹的硬时间窗约束，以最小化分拣作业周期为优化目标，分别建立了混合整数规划（mixed integer programming，MIP）模型和约束规划（constraint programming，CP）模型。通过算例试验结果，验证了CP模型的有效性，通过对CP模型的可拓展性进行分析，表明了CP模型的灵活性。此外，还分析了不同AGV数量和充电率对优化目标的影响。

1 问题描述

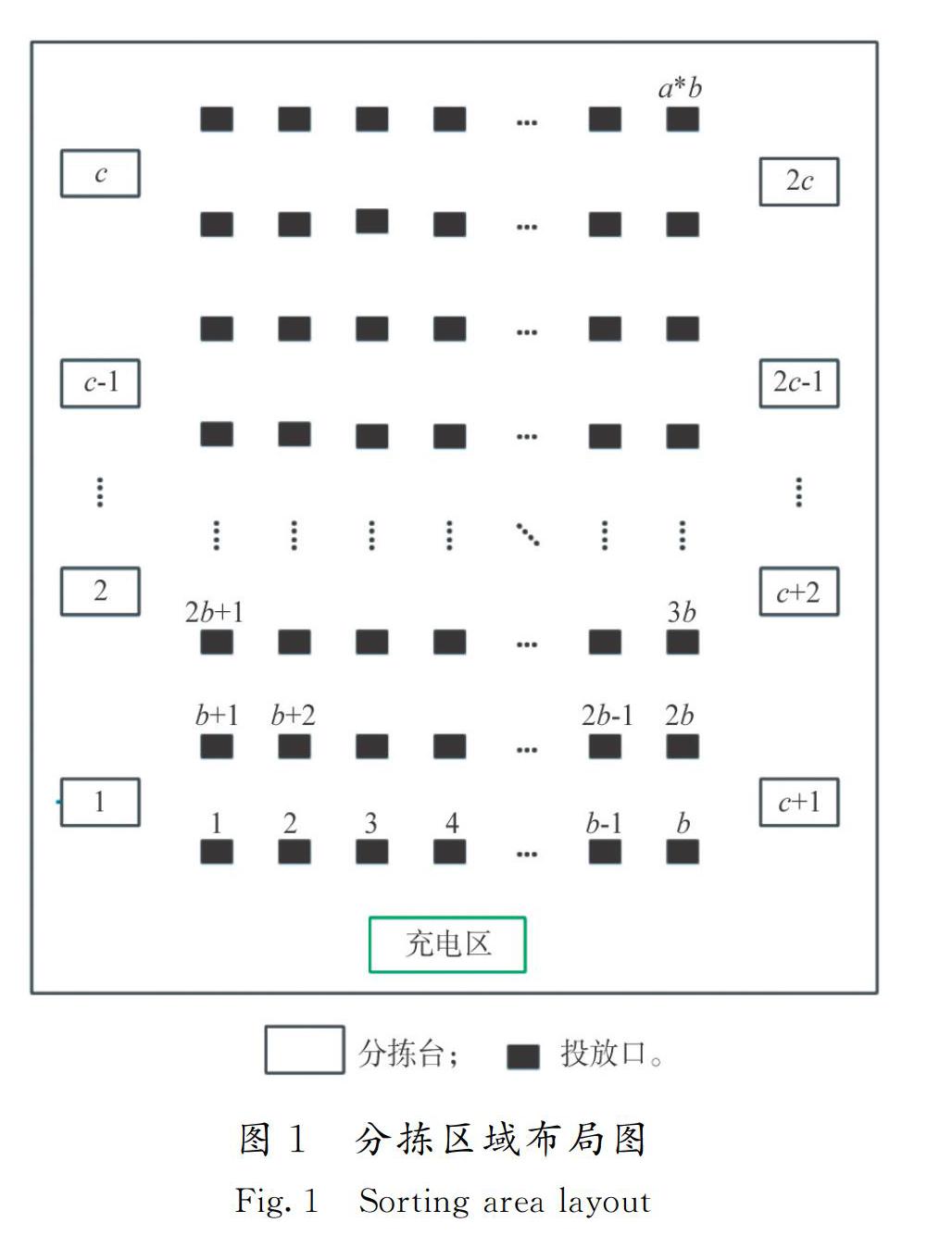
物流分拣中心通常由入库区、出库区、分拣区等组成，而分拣区又由分拣台、投放口、AGV充电区（停放区）等组成。本文借鉴文献[19]中的分拣区布局方式，如图1所示。在分拣区内，来自不同地区的包裹入库后随着传送带到达各个分拣台，AGV接收到搬运任务后前往包裹所在的分拣台。AGV到达分拣台后需要根据包裹上的运单信息，将其运送至对应的投放口，每个投放口代表不同的配送地区。在投放口下方是漏斗和传送带，它们会收集包裹并将其运送至出库区，在出库区会有车辆进行下一阶段的配送。

基于以上应用场景，给定包裹集合N={1，2，…，n}，其中n为包裹总数。给定AGV集合K={1，2，…，m}，其中m为AGV数量。AGV在不工作时都停靠在充电区，当接收到任务时，AGV从充电区出发前去搬运包裹。每个包裹i（i∈N）都有相应的最早到达时间ei、搬运时间ti和最晚完工时间di。最晚完工时间di用于保证包裹分拣出库后派送车辆的时间安排，因此每个包裹到达投放口的时间不能晚于该时间，否则将影响后续的车辆配送。

AGV搬运一个包裹通常需要经历3个阶段：第1个阶段是从当前位置前往包裹所在的分拣台，此时AGV处于空载阶段;第2个阶段是若AGV在ei之前到达分拣台，存在等待阶段，反之则不存在此阶段;第3阶段是AGV在分拣台装载包裹，运到对应的投放口，此时是负载阶段。每运送完一个包裹，AGV会检查当前电量是否低于安全电量g。当电量充足时，AGV直接前往下一包裹所在分拣台;当电量不足时，AGV需要前往充电区充电，充电完成后再到下一包裹所在的分拣台。如此反复，直至所有运输任务执行完毕，最后返回充电区。

本文模型存在的约束条件及假设如下：

1）当AGV运送一个包裹时，会选择最短路径，最短路径距离由AGV的起点和终点用曼哈顿距离唯一确定;

2）每辆AGV从充电区出发时都为满电量状态;

3）AGV可以停留在装卸位置（分拣台/投放口）;

4）每辆AGV一次只能装载一个包裹，即每辆AGV只能同时执行一个包裹的运输工作;

5）AGV的安全电量大于从任意投放口返回充电区所需的电量，以满足AGV在执行完搬运任务后有足够的电量返回充电区充电;

6）每辆AGV的运输效率相同，空载和负载的运行速度及耗电量不变;

7）不考虑AGV在运行过程中可能产生的冲突和每次装卸包裹的时间。

2 数学模型

2.1 MIP模型

假设物流分拣中心共有n个包裹需要分拣，由m辆AGV共同工作来完成所有作业任务。本文以最小化分拣作业周期为目标建立混合整数规划模型，相關符号的定义如下所示。

N为任务集合，N={1，2…，n};N+：N+=N∪{0，n+1}，0和n+1分别表示虚拟开始任务和虚拟结束任务;K为AGV集合，K={1，2，…，m};Q为AGV的最大电池电量;g为AGV的安全电量;μ为AGV充电率;κ为AGV电量消耗率;M为一个足够大的数;tij 为从任务i的投放口到任务j的分拣台所需的时间，若i=0或n+1，则对应的点为充电区，因此t0，j表示从充电区到任务j的分拣台所需的时间，ti，n+1表示从任务i的投放口到充电区所需的时间;hi为从任务i的分拣台到任务i的投放口所需的时间，当任务i为虚拟开始（结束）任务时，hi则为零;Cmax为分拣作业周期，即最大完工时间;ei为任务i到达分拣台的时间;di为任务i的最晚完工时间;ski为任务i开始被AGVk执行的时间;rki为AGVk完成任务i后的剩余电量;bki为AGVk完成任务i后去充电区并充满电所需的时间;xkij为0或1，若AGVk在完成任务i后执行任务j则为1，否则为0;zki为0或1，若AGVk执行完任务j后需要去充电则为1，否则为0。

建立的混合整数规划模型如下：

Obj：

min Cmax。（1）

s.t.

∑k∈K∑j∈N+xkij=1， i∈N，（2）

∑k∈K∑i∈N+xkij=1， j∈N，（3）

∑i∈N+xkij-∑i∈N+xkji=0， j∈N， i≠j， k∈K，（4）

∑i∈N+xk0，i≤1， k∈K，（5）

∑i∈N+xki，n+1≤1， k∈K，（6）

Cmax≥ski+hi， i∈N， k∈K，（7）

skj+M（1-xkij）+M·zki≥ski+hi+tij， i，j∈N+， i≠j， k∈K，（8）

skj+M（1-xkij）+M（1-zki）≥ski+hi+bki+t0，j， i，j∈N+， i≠j， k∈K，（9）

ski≥ei， i∈N+， k∈K，（10）

ski+ti≤di， i∈N+， k∈K，（11）

g≤rki≤Q， i∈N+， k∈K，（12）

bki+M（1-zki）≥ti，n+1+μ（Q-rki+κ·ti，n+1）， i∈N+， k∈K，（13）

rkj≤Q-κ（t0，j+hj）+M（1-zki）+M（1-xkij）， i，j∈N+， i≠j， k∈K，（14）

rkj≤rki-κ（tij+hj）+M·zki+M（1-xkij）， i，j∈N+， i≠j， k∈K。（15）

目标函数（1）表示最小化最大完工时间，约束（2）和（3）表示每个任务都必须被执行且只能被1辆AGV执行1次;约束（4）表示对任意AGV和非虚拟任务，应满足任务网络流约束;约束（5）和约束（6）分别表示每辆AGV都要从虚拟起点出发，最后返回虚拟终点;约束（7）使最大完工时间大于或等于任何一次搬运任务的完成时间;约束（8）表示如果AGVk执行完任务i后执行任务j，且在执行完任务i时电量充足（即：xkij=1且zki=0），则任务i，j的开始执行时间满足skj≥ski+hi+tij;约束（9）表示如果AGVk执行完任务i后执行任务j，且在执行完任务i时电量不足（即：xkij=1且zki=1），则任务i，j的开始执行时间满足skj≥ski+hi+bki+t0，j;约束（10）表示每个任务的开始执行时间要晚于其最早可被执行的时间;约束（11）表示每个任务的完工时间不能晚于其最晚完工时间;约束（12）为AGV电量约束;约束（13）表示AGVk在完成任务i后若需要充电，则去到充电区并充满电所需的时间;约束（14）表示如果AGVk执行完任务i后执行任务j，且在执行完任务i后需要充电（即：xkij=1且zki=1），则执行完任务j后的电量;约束（15）表示如果AGVk执行完任务i后执行任务j，且在执行完任务i后无需充电（即：xkij=1且zki=0），则执行完任务j后的电量。

2.2 CP模型

近年来，起源于人工智能研究领域的约束规划技术在车辆路径优化[20-21]、车间作业调度[22-23]、任务计划[24]等多种组合优化问题中获得了越来越多的关注和应用。目前还没有将CP应用于分拣中心多AGV调度这一复杂问题，因此本文提出并建立CP模型，与传统的混合整数规划作对比。与混合整数规划相比，CP关注的是约束条件和可行性，而不是目标函数和最优性。由于CP模型在不同的CP求解器中表示方法和建模方法均不一致，本文所建CP模型基于IBM ILOG CPLEX Optimization 12.10.0中的OPL 12.10.0语言实现，因此使用该语言的语法构造，涉及的变量和约束的语法如下。

1）intervaLVar（s，e，l，）：区间变量，表示执行某个任务的时间间隔，其中s，e，l分别表示任务的开始时间、结束时间和持续时间，参数表示该任务是否存在是可选的。

2）sequenceVar（{α1，α2，…，αn}）：序列变量，由一组区间变量α组成，表示一组待执行的任务序列。

3）alternative（α，B）：若区间变量α存在，则集合B={α1，α2，...，αn}中有且仅有一个区间变量存在，且2个区间变量的开始时间和结束时间一致。

4）prev（seq，α1，α2）：若区间变量α1和α2均存在于序列变量seq中，则在seq中α1位于α2之前。

5）if_then（e1，e2）：若布尔表达式e1为真，则布尔表达式e2也为真。

6）presence_of（α）：若区间变量α存在，則返回1，否则返回0。

7）noOverlap（seq，T）：序列变量seq中的所有区间变量之间的时间间隔必须满足转移时间矩阵T，从而使得所有区间变量在时间上不会发生干扰。

8）stepAtStart（α，h）：基本累积函数，用来表示活动对资源的累积使用情况，α表示对资源量有影响的区间变量，h表示区间变量α在执行过程中对资源量的影响值。

9）heightAtStart（α，f）：区间变量α在其开始时间点对基本累积函数f的影响。

10）alwaysln（f，α，min，max）：累积函数f在区间变量α的时间间隔内时，其可能值始终限制在特定的范围内。此外，α也可以是一个时间区间。

11）first（seq，α）：若区间变量α存在于序列变量seq中，则它必须位于序列的首位。

12）last（seq，α）：若区间变量α存在于序列变量seq中，则它必须位于序列的末位。

在CP模型中，将所有的任务定义为具有开始时间、持续时间和结束时间的区间变量。表示搬运任务的区间变量Xi的持续时间l=hi，表示充电任务的区间变量Cki的持续时间l为最大电量与当前电量的差值。由于AGV在每完成一个搬运任务后都需要检查当前电量是否低于安全电量，若当前电量低于安全电量，则Cki存在，反之则不存在。任务序列中的每个区间变量之间存在时间间隔，从而确保了任意区间变量在时间上不会发生重叠，该时间间隔实际上是指tij。CP模型中部分参数与MIP模型中的定义相同，其他参数和变量的定义如下所示。

T为各个任务点之间的转移时间矩阵，T=;H为一个足够大的整数，表示计划期长度，也是完工时间的上界;Xi为区间变量，表示搬运任务i;Xki为可选区间变量，表示任务i分配给AGVk来完成;Cki为可选区间变量，表示AGVk完成任务i后的充电任务;Xk0为区间变量，表示AGVk的虚拟开始任务;Xkn+1为区间变量，表示AGVk的虚拟结束任务;Sk为序列变量，表示分配给AGVk的待执行任务序列;Qk为汇总累积函数，表示AGVk在工作过程中的电量;Pki为累积函数，表示AGVk执行任务i时消耗的电量;Rki为累积函数，表示AGVk执行任务i后的充电任务时消耗的电量。

建立的约束规划模型如下所示：

Obj：

min（max（endOf（Xi））），i∈N，（16）

s.t.

alternative（Xi，{X1i，X2i，...Xmi}），i∈N，（17）

prev（Sk，Xki，Cki），i∈N，k∈K，（18）

if_then（presence_of（Cki），presence_of（Xki）），i∈N，k∈K，（19）

noOverlap（Sk，T），k∈K，（20）

Qk=stepAtStart（Xk0，Q）-

∑i∈NstepAtStart（Xki，κ·（tPrevSk（i），i+hi））+

∑i∈NstepAtStart（Cki，（μ·length（Cki）-κ·ti，n+1）），k∈K，（21）

alwaysIn（Qk，，），k∈K，（22）

alwaysIn（Qk，Cki，），k∈K，（23）

first（Sk，Xk0）k∈K，（24）

last（Sk，Xkn+1），k∈K，（25）

Sk：sequenceVar（{Xk0，Xk1，...，Xkn+1}），k∈K，（26）

Xi：intervalVar（hi，，），i∈N，（27）

Xki：optlntervalVar（hi，，），i∈N，k∈K，（28）

Cki：optlntervalVar（，），i∈N，k∈K，（29）

Xk0：intervalVar（0，），k∈K，（30）

Xkn+1：intervalVar（0，），k∈K。（31）

上述模型中，目標函数（16）表示最小化最大完工时间;约束（17）表示将每个搬运任务分配给一辆AGV;约束（18）确保对于给定的AGV在执行完该搬运任务后若电量不足要去执行充电任务，则该搬运任务和充电任务之间不能安排其他任务;约束（19）表示若存在该充电任务，则在充电任务前的搬运任务也一定存在;约束（20）表示每辆AGV的任务序列在时间上无重叠，T为转移时间矩阵，定义了序列中必须分隔2个连续区间的最小时间;约束（21）和（22）保证了每辆AGV的电量始终保持在可允许的范围内，其中κ·（tPrevSk（i），i+hi）表示AGV搬运任务对电量的负面影响，κ·ti，n+1表示AGV前往充电区对电量的负面影响，μ·length（Cki）表示AGV充电对电量的正面影响，三者都以累积函数表达式来表示;约束（23）表示AGV充电时会充到满电量再出发;约束（24）表示所有AGV都是从充电区出发;约束（25）表示所有AGV最后都要回到充电区;约束（26）—（31）定义了各个区间变量和序列变量。

由于函数stepAtStart（α，h）中的高度h必须是一个整数或2个整数组成的区间，而每个任务对AGV电量的影响值tPrevSk（i），i和length（Cki）是变量，所以CP Optimizer暂不支持此类型参数。为了解决这一问题，可以通过使用函数heightAtStart（α，f）给定区间变量α对累积函数f的电量影响值，因此需要将约束（21）等价替换为约束（32）—（36）便可解决该类问题。

Qk=stepAtStart（Xk0，Q）-∑i∈NPki+∑i∈NRki，k∈K，（32）

Pki=stepAtStart（Xki，（0，Q）），i∈N，k∈K，（33）

heightAtStart（Xki，Pki）=κ·（tPrevSk（i），i+hi），i∈N，k∈K，（34）

Rki=stepAtSate（Cki，（0，Q）），i∈N，k∈K，（35）

heightAtStart（Cki，Rki）=μ·length（Cki）-κ·ti，n+1，i∈N，k∈K。（36）

3 数值算例分析

针对混合整数规划模型，使用8.1.1版本的Gurobi优化求解器进行计算，对于约束规划模型，使用IBM ILOG CPLEX Optimization Studio 12.10.0版本的CP Optimizer求解。2个模型均由Python语言实现，所有的算例运算在配置为AMD Ryzen 5-4600U with Radeon Graphics CPU @ 2.10 GHz，16.0 GB的个人电脑上运行。

为了便于分析算法的性能，本文引入相对百分比偏差（relative percentage difference，RPD）能更加直观地对比试验结果，其计算公式为RPD=Ccurent-CbestCbest×100%。（37）

式（37）中：Ccurent表示当前方法求得的目标值;Cbest为该算例在所有方法中取得的最优目标值。因此，RPD值越小，表示该方法求解效果越好。

3.1 算例设计

为验证约束规划模型的有效性，以图2所示的分拣区规模为仿真实例，图中分拣台用白色长方块表示，投放口用黑色小方块表示，x和y轴上每单位表示2 m。任意位置都有其对应的坐标，例如：充电区的坐标为（5，1），投放口6的坐标为（7，2），分拣台6的坐标为（9，7），投放口42的坐标为（8，12）。AGV每行驶一单位长度需要一单位时间，由此可以获得任意点间的时间矩阵。

结合以上应用场景数据，设计物流分拣中心多AGV调度问题的测试算例。首先，每个包裹的分拣点和投放点分别从整数均匀分布[1，8]和[1，56]中随机选择，由此可以获得每个包裹的搬运时间ti。假设第k辆AGV的最早可用时间ak=0，AGV从当前位置前往包裹i的分拣点所需时间的bi从整数均匀分布[2，20]中随机选择。然后，将任务先后分配给可用的AGV，保存每个包裹在初始调度中的开始搬运时间si=mink∈K{ak}+bi，并在每次分配后更新AGV的最早可用时间aargmink∈K{ak}=mink∈K{ak}+bi+ti。以上步骤生成了一个初始调度方案，以保证每个算例的可行性。

接下来，生成每个包裹的时间窗。对于每个包裹的时间窗大小αi从区间[2，3]中随机选择，从区间[0，1]中选择一个随机数βi，用于确定包裹i在时间窗内的初始位置。考虑到充电需求这一因素，为保证算例的可行性，需要在时间窗中考虑充电时间ci，该时间从整数均匀分布[100，120]中随机选择。最后，基于以上数据，生成每个包裹的时间窗上界ei=si-ti·（αi-1）·βi和时间窗下界di=si+ti·+ci。

将AGV电容量用单位电量表示，1个单位电量为1 AH。设置AGV的参数配置为最大电容量Q=100;安全电量g=20;充电率μ=1 AH/s，表示一单位时间可以充一个单位的电量;电量消耗率κ=1 AH/m，表示行驶一单位长度需要消耗一个单位的电量。算例分为小规模算例和大规模算例，针对小规模算例，设置为包裹数n={8，10，14}，AGV数m={2，3，4};针对大规模算例，设置包裹数n=50，AGV数m={10，15，20}。可以得到不同规模的算例12组，为每组随机生成4个，共计48个算例。

3.2 计算结果与分析

在计算中，将Gurobi和CP Optimizer的最大求解时间均设置为1 800 s，若在给定时间内未找到最优解，则停止计算并返回当前已知最优可行解。表1和表2中J表示待搬运包裹数量，V表示AGV数量，No.表示該组算例的序号，MIN表示该算例求得的最小目标函数值。每个方法均列出了目标值、计算时间和RPD，对比了小规模算例和大规模算例分别在MIP模型和CP模型中的计算结果。

表1给出了小规模算例的计算结果。从表1中可以看到，2个模型在大部分算例中都能求得相同的解，这证明了MIP模型和CP模型的正确性。从计算时间上来看，CP模型在25个算例中的计算时间均小于MIP模型，且CP模型的平均计算时间为300.76 s，远小于MIP模型的平均计算时间。从求解精度上来看，MIP模型的平均RPD值为2.78，而CP模型的平均RPD值为0.00。在算例10-2-4和14-2-1中，MIP模型未能在规定时间内找到最优解，而CP模型却在极短时间内找到了最优解。由以上3点可以看出，相较于MIP模型，同为精确算法的CP模型在各方面的求解性能更优。

大规模算例的计算结果如表2所示。由于本问题为NP-hard问题，当包裹数为50时，MIP模型仅有4个算例能找到近似解，其余8个算例耗费了1 800 s仍不能找到可行解。而CP模型有9个算例能在短时间

内找到最优解，仅有2个算例在规定时间内未能找到可行解。从计算时间上来看，CP模型的平均计算时间为495.75 s，远小于MIP模型的平均计算时间，且在AGV数为15和20的所有算例中，CP模型的平均计算时间仅为23.87 s。由此可见，CP模型在解决分拣中心考虑充电需求和硬时间窗的大规模多AGV调度问题上更有优势。

3.3 AGV配置分析

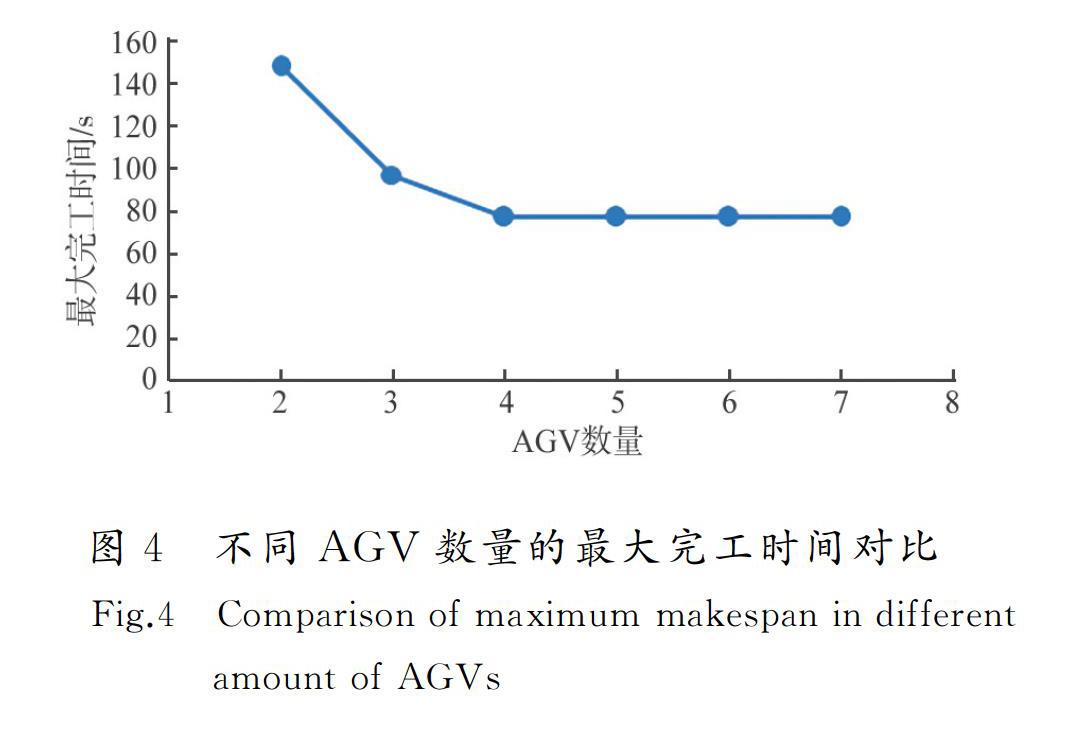
充电率配置的不同将导致AGV充电速率不一样，参数配置越高充电率越大，即充电速度越快。不同的AGV充电率会导致AGV充电所需时间不同，从而影响分拣的总完工时间。此外在一定的分拣作业量下，不同的AGV数量配置同样会影响分拣完工时间。对于运营方而言，AGV的配置越高，其采购成本也就越高，但如果AGV的配置过低，又会导致分拣任务无法按时完成或分拣效率过低，因此找到合适的AGV充电率配置和数量配置对于物流收益有非常大的影响。本文以包裹数n=14，AGV数m=2的算例来分析不同AGV充电率对总完工时间的影响。以包裹数n=14，AGV数m={2，3，4，5，6，7}的算例来分析AGV数量对总完工时间的影响。

圖3为不同的AGV充电率与最大完工时间关系对比，横坐标为AGV充电率，纵坐标为最大完工时间。从图3可以看出，当充电率大于1.6 C/s时，最大完工时间降幅明显放缓，因此，最合适的AGV充电率为1.6 C/s。图4是不同AGV数量配置与最大完工时间关系对比，横坐标为AGV数量，纵坐标为最大完工时间。由图4可见，当AGV数量大于4时，最大完工时间不再发生变化。可以得出，当包裹数为14时，最多只需配置4辆AGV。

3.4 拓展分析

本文参考了文献[19]中的分拣区布局方式，该文献考虑了搬运不同包裹时AGV采用不同的速度，AGV的电量消耗率也随速度的变化而变化。在实际的分拣场景中，AGV的行驶速度会因为搬运包裹的重量不同而存在一定的差异，由于本文的应用场景是分拣小型包裹，因此对微小的速度差异忽略不计，假定AGV速度不变。由于该文献未说明AGV的行驶速度和电量消耗率的取值方式，因而本文无法使用其提供的数据进行计算后作对比分析。但本文提出的约束同样可以适用于求解该文献中的问题，考虑到部分因素的差异，需要做出如下拓展。

1）本文考虑了每个包裹的最晚分拣完成时间，而该文献中未考虑这一重要因素，因此可以将最晚完工时间设为一个极大的数M，只需将CP模型中的约束（27）和（28）改为

Xi：intervalVar（hi，，），i∈N，

Xki：optlntervalVar（hi，，），i∈N，k∈K。

2）该文献中在目标函数中额外考虑了最小化车辆数和耗电量。在实际应用场景中，分拣中心的主要目标是在尽可能短的时间内分拣完所有的包裹，并且保证所有的包裹能够在其最晚分拣完成时间之前送达对应的投放口。因此本文未在目标函数中考虑这2个因素，但本文提出的CP模型具有良好的可拓展性，若需要加入最小化车辆数和耗电量，仅需对CP模型中的式（16）做如下调整：

min（∑k∈Kpresence_of（Xk0）+max（endOf（Xi））+∑k∈K（Q-Qkn+1+length_of（Cki））），i∈N。

调整后的目标函数中的∑k∈Kpresence_of（Xk0）表示从充电区出发的AGV数量，即参与到分拣作业中的AGV数量;∑i∈Nlength_of（Cki）表示AGVk充电时增加的电量;Qkn+1表示AGVk完成所有任务后回到充电区的剩余电量，每辆车消耗的电量由初始电量、最终剩余电量和充电所得电量求得。因此，∑k∈K（Q-Qkn+1+∑i∈Nlength_of（Cki））表示所有车辆的总耗电量。

3）若需要考虑AGV搬运不同包裹时设置不同的行驶速度和电量消耗率，则只需将给定的行驶速度和电量消耗率设置为一定范围内的变量即可。

通过以上对CP模型的拓展操作，可以将其他约束集成到本文的调度问题中。由此说明提出的多AGV调度问题和解决方案模型具有高度的灵活性，可适用于考虑不同因素的多种场景。

4 结 语

1）为进一步缩短包裹的分拣时间并提高AGV的分拣效率，针对物流分拣中心包裹分拣过程，从AGV采用纯电力驱动和包裹分拣完成后需进行下一步配送这2个实际情况出发，研究了带有充电需求和硬时间窗约束的多AGV调度问题。

2）建立了考虑AGV搬运作业和充电需求的混合整数规划模型，并提出将约束规划技术应用于解决这一复杂调度问题，使用区间变量表示任务执行情况，借助累积函数更加直观地表述电量的变化情况。

3）通过使用OPL高级建模语言建立，并利用CP Optimizer进行了求解。不同规模的算例结果表明，CP模型比MIP模型拥有更优的求解性能。

4）本文基于混合整数规划与约束规划技术实现了物流分拣中心AGV调度优化，但所构建的模型在处理大规模算例时存在求解时间过长的问题，在未来的研究中有必要针对问题特性设计基于变邻域搜索或群集智能优化算法的启发式调度策略。此外，关于AGV工作过程中自动处理路径冲突的问题也值得思考，以保证调度系统能够处理分拣过程中的实时信息，更贴近实际作业过程。

参考文献/References：

[1] 李明，吴耀华，吴颖颖，等.人工与自动化双分拣区系统品项分配优化[J].机械工程学报，2015，51（10）：197-204.

LI Ming，WU Yaohua，WU Yingying，et al.Items assignment optimization for double picking zones with manual picking system and automated picking system [J].Journal of Mechanical Engineering，2015，51（10）：197-204.

[2] ZHAN M，YU K.Wireless communication technologies in automated guided vehicles：Survey and analysis[C]//IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society.Washington：IEEE，2018：4155-4161.

[3] BOYSEN N，DE KOSTER R，WEIDINGER F.Warehousing in the e-commerce era：A survey[J].European Journal of Operational Research，2019，277（2）：396-411.

[4] OYEKANLU E A，SMITH A C，THOMAS W P，et al.A review of recent advances in automated guided vehicle technologies：Integration challenges and research areas for 5G-based smart manufacturing applications[J].IEEE Access，2020，8：202312-202353.

[5] ZACHARIA P T，XIDIAS E K.AGV routing and motion planning in a flexible manufacturing system using a fuzzy-based genetic algorithm[J].The International Journal of Advanced Manufacturing Technology，2020，109（7/8）：1801-1813.

[6] MOHAMMADI E K，SHIRAZI B.Toward high degree flexible routing in collision-free FMSs through automated guided vehicles dynamic strategy：A simulation metamodel[J].ISA Transactions，2020，96：228-244.

[7] CHAWLA V K，CHANDA A K，ANGRA S，et al.Effect of nature-inspired algorithms and hybrid dispatching rules on the performance of automatic guided vehicles in the flexible manufacturing system [J].Journal of the Brazilian Society of Mechanical Sciences and Engineering，2019，41（10）：1-17.

[8] BOYSEN N，BRISKORN D，EMDE S.Parts-to-picker based order processing in a rack-moving mobile robots environment[J].European Journal of Operational Research，2017，262（2）：550-562.

[9] 袁瑞萍，王慧玲，孙利瑞，等.基于物流AGV的“货到人”订单拣选系统任务调度研究[J].运筹与管理，2018，27（10）：133-138.

YUAN Ruiping，WANG Huiling，SUN Lirui，et al.Research on the task scheduling of “goods to picker” order picking system based on logistics AGV[J].Operations Research and Management Science，2018，27（10）：133-138.

[10]賀学成，吕淑静，吕岳.高密集度AGV快递包裹分拣系统的路径规划[J].计算机系统应用，2019，28（4）：39-44.

HE Xuecheng，LYU Shujing，LYU Yue.Path planning of high density AGV parcel sorting system[J].Computer Systems & Applications，2019，28（4）：39-44.

[11]XING L N，LIU Y Y，LI H Y，et al.A novel tabu search algorithm for multi-AGV routing problem[J].Mathematics，2020，8（2）：279.

[12]余娜娜，李铁克，王柏琳，等.自动化分拣仓库中多AGV调度与路径规划算法[J].计算机集成制造系统，2020，26（1）：171-180.

YU Nana，LI Tieke，WANG Bailin，et al.Multi-AGVs scheduling and path planning algorithm in automated sorting warehouse[J].Computer Integrated Manufacturing Systems，2020，26（1）：171-180.

[13]MCHANEY R.Modelling battery constraints in discrete event automated guided vehicle simulations[J].International Journal of Production Research，1995，33（11）：3023-3040.

[14]KARIMI B，NIAKI S T A，HALEH H，et al.Bi-objective optimization of a job shop with two types of failures for the operating machines that use automated guided vehicles[J].Reliability Engineering and System Safety，2018，175：92-104.

[15]AIZED T.Modelling and performance maximization of an integrated automated guided vehicle system using coloured Petri net and response surface methods[J].Computers & Industrial Engineering，2009，57（3）：822-831.

[16]MOUSAVI M，YAP H J，MUSA S N，et al.Multi-objective AGV scheduling in an FMS using a hybrid of genetic algorithm and particle swarm optimization[J].PLoS One，2017，12（3）：e0169817.

[17]周小凡，苌道方，余芳，等.考虑充电和等待时间的集装箱码头AGV调度[J].上海海事大学学报，2019，40（3）：1-5.

ZHOU Xiaofan，CHANG Daofang，YU Fang，et al.Scheduling of AGV in container terminals considering charging and waiting time[J].Journal of Shanghai Maritime University，2019，40（3）：1-5.

[18]张亚琦，杨斌，胡志华，等.自动化码头AGV充电与作业的集成调度研究[J].计算机工程与应用，2017，53（18）：257-262.

ZHANG Yaqi，YANG Bin，HU Zhihua，et al.Research of AGV charging and job integrated scheduling at automated container terminal[J].Computer Engineering and Applications，2017，53（18）：257-262.

[19]LIU Y，JI S，SU Z，et al.Multi-objective AGV scheduling in an automatic sorting system of an unmanned （intelligent） warehouse by using two adaptive genetic algorithms and a multi-adaptive genetic algorithm[J].PLoS One，2019，14（12）：e0226161.

[20]HAM A M.Integrated scheduling of m-truck，m-drone，and m-depot constrained by time-window，drop-pickup，and m-visit using constraint programming[J].Transportation Research Part C：Emerging Technologies，2018，91：1-14.

[21]SCHUIJBROEK J，HAMPSHIRE R C，van HOEVE W J.Inventory rebalancing and vehicle routing in bike sharing systems [J].European Journal of Operational Research，2017，257（3）：992-1004.

[22]HAM A.Transfer-robot task scheduling in flexible job shop [J].Journal of Intelligent Manufacturing，2020，31（7）：1783-1793.

[23]孟磊磊，張超勇，邵新宇，等.基于约束规划的焊接车间多资源约束调度研究[J].华中科技大学学报（自然科学版），2018，46（6）：1-7.

MENG Leilei，ZHANG Chaoyong，SHAO Xinyu，et al.Constraint programming for multi-resource constrained welding shop scheduling[J].Journal of Huazhong University of Science and Technology （Natural Science Edition），2018，46（6）：1-7.

[24]BOOTH K E C，TRAN T T，NEJAT G，et al.Mixed-integer and constraint programming techniques for mobile robot task planning[J].IEEE Robotics and Automation Letters，2016，1（1）：500-507.