动态锁定螺钉固定胫骨远端骨折的有限元分析

杨卫强，赵永明，丁 童，张立凯，方 远，貟 霄，郭新军，蒋振刚，王培山

（新乡市中心医院a骨科；b麻醉科，河南新乡 453003）

胫骨远端骨折通常是高能暴力导致的干骺端骨折，目前常用的治疗方案为复位后应用钢板或髓内钉内固定。相对于动力加压钢板（dynamic compression plate,DCP），锁定加压钢板（locking compression plate,LCP）通过螺钉与钢板之间锁定，实现整个内固定系统的角度稳定，可有效避免螺钉和钢板对骨表面的压力和摩擦力，同时使应力更均匀的分布，从而显著增强内固定对抗轴向负荷的强度［1］。但在临床应用中，LCP治疗的部分患者中会出现钢板骨皮质骨不连或骨折延迟愈合的现象［2］。随着BO骨折愈合理论的推广，人们在LCP的基础上设计出动态锁定螺钉（dynamic locking screws,DLS）［3］，该内固定系统通过去除钢板侧皮质的锁定螺纹，将全螺纹固定转换为以螺钉顶端与对侧皮质为支点的悬臂梁结构，从而实现了骨折端的微动。本研究采用有限元分析的方法研究DCP、LCP和DLS治疗胫骨远端骨折的应力分布特点，为临床正确的认识动态锁定钢板提供帮助。

1 资料与方法

1.1 胫骨三维模型的建立

选取1例37岁男性志愿者的下肢CT图像。纳入标准：无下肢畸形、无外伤及手术史、无骨与软组织肿瘤病变。扫描范围：股骨中下段至足底。将获得的患者下肢CT图像在医学图像处理软件Mimics 14.0中，划分出胫腓骨的皮质骨、松质骨三维点云模型。导入Geomagic Studio10.0，对胫腓骨的点云模型进行封装，拟合胫腓骨的Nurbs曲面模型，以.iges格式导入软件Cero3.0中进行装配，在胫骨远端干骺端横形切除2 mm宽的骨质，建立胫骨远端骨折模型。

1.2 内固定系统有限元模型

在Cero3.0中，参考临床常用的各种内固定钢板的参数（山东威高医疗器械有限公司提供），建立前外侧DCP、LCP及DLS内固定的三维模型，分别构建各内固定系统螺钉，将上述模型分别进行装配。

1.3 有限元模型应力施加

在Hypermesh13.0中，调整模型的坐标系，使XZ平面为冠状面，YZ平面为矢状面，XY平面为横断面，坐标系原点位于下胫腓联合的中点。划分2D单元网格，参数为1.5 mm，最小角度控制在30°，划分完整后，优化局部钉孔部位的网格质量。为减少计算量，在本研究LCP模型中，螺钉与钢板之间、螺钉与皮质骨之间设定为共节点连接。DCP模型中，螺钉与皮质骨之间为共节点连接，螺帽与钢板之间为滑动接触，预紧力为80 N。DLS模型中，螺帽与钢板之间、螺钉与对侧骨皮质之间均为共节点连接，螺钉与同侧骨皮质之间不设置接触关系，各模型见图1。参照相关文献，为各组件赋予其力学属性［4，5］。见下表1。

表1 本研究中材料的力学参数及单元数据

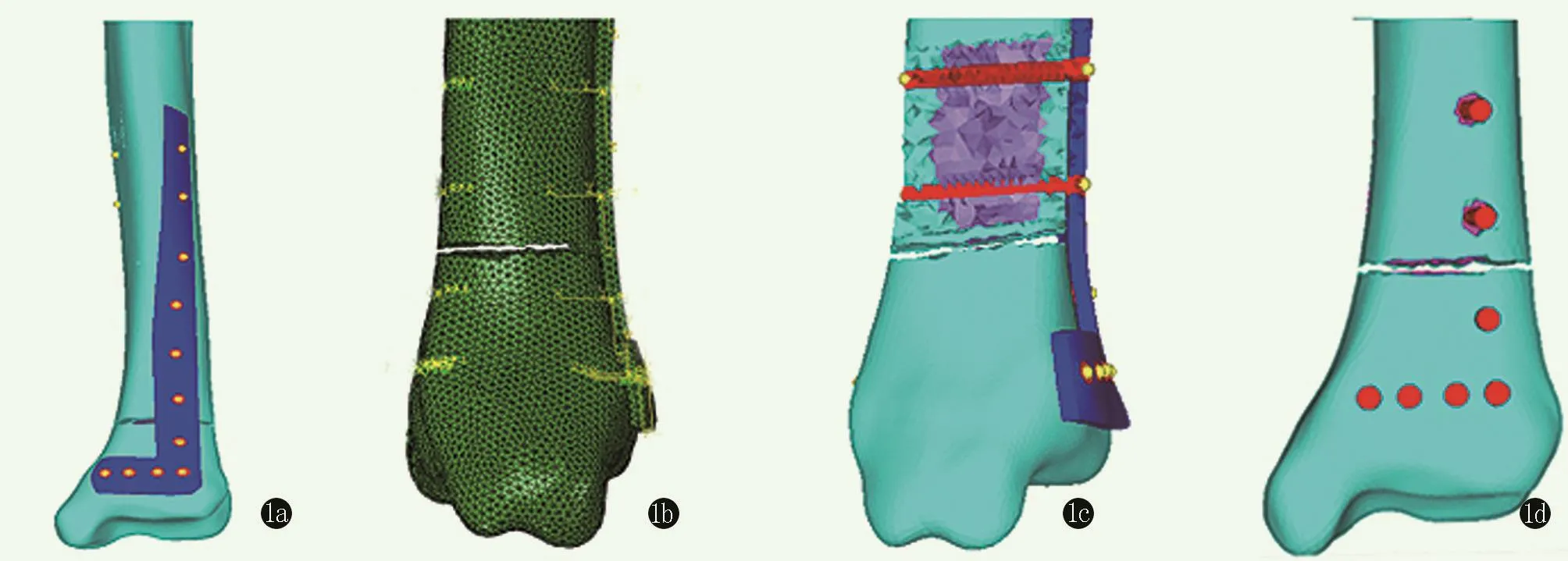
图1 各内固定系统的有限元模型 1a:胫骨远端外侧钢板及骨折类型 1b:DCP模型中螺钉拉力通过添加预紧力模拟 1c:LCP模型螺钉与骨质及钢板的绑定关系 1d:DLS模型中显示骨折近端皮质骨螺钉钢板侧钉道扩大，模拟动态锁定螺钉与钢板的连接关系

将上述模型导入Abaqus6.14中，以胫骨远端关节面为边界条件，在胫骨近端关节内外侧髁关节面中心节点分别建立MPC约束。本研究参考相关文献进行以下3种载荷：其中垂直载荷为胫骨近端两关节面加载400 N、800 N。弯曲载荷为胫骨内侧关节面加载400 N、800 N。扭转载荷为垂直于Z轴施加大小为 400 N/mm、800 N/mm［6］。

1.4 测量指标

在轴向载荷、弯曲载荷及扭转载荷工况中，测量骨折间隙的相对位移量、骨折间隙上下方螺钉及骨折间隙处钢板平均应力。应力遮挡率（η）：η=（1-σ1/σ2）100%，σ1为固定时骨的应力大小，σ2为正常对照模型中相应位置的应力大小［5］。

1.5 统计学方法

2 结果

2.1 位移测量结果

轴向载荷下骨折端位移量随着载荷的增大而显著增加，其中800 N载荷产生的位移量显著大于400 N载荷产生的位移量（P＜0.05）。相同载荷量作用下，弯曲载荷产生的位移量显著大于轴向载荷的位移量，差异有统计学意义（P＜0.05），而扭转载荷产生的位移量要小于轴向载荷的位移量，差异有统计学意义（P＜0.05）（表 2）。

表2 三种固定方式骨折端相对位移量（mm，±s）与比较

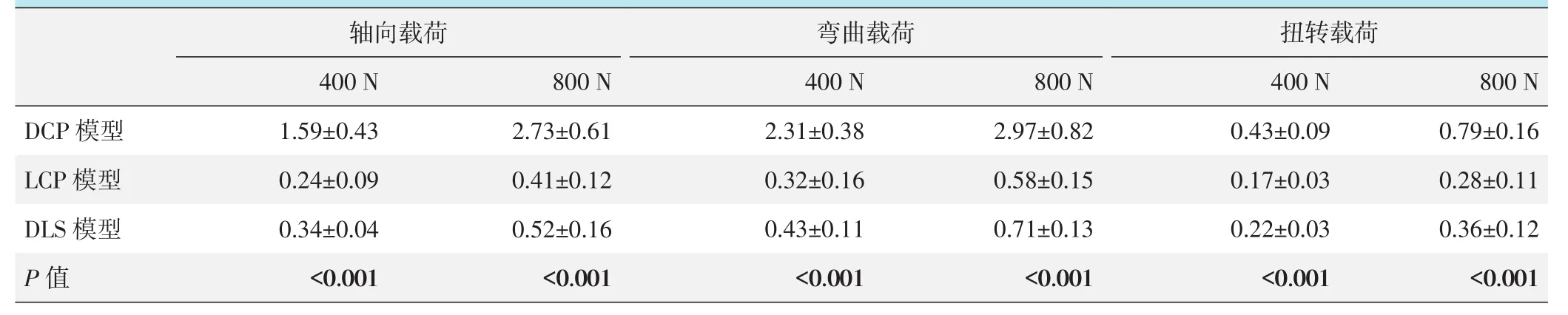
表2 三种固定方式骨折端相对位移量（mm，±s）与比较

images/BZ_74_204_1457_422_1589.pngimages/BZ_74_422_1457_1023_1523.png1.59±0.43 0.34±0.04images/BZ_74_1035_1457_1674_1523.png2.31±0.38 0.43±0.11images/BZ_74_1686_1457_2276_1523.pngimages/BZ_74_422_1523_708_1589.pngimages/BZ_74_708_1523_1023_1589.png2.73±0.61 0.52±0.16images/BZ_74_1035_1523_1364_1589.pngimages/BZ_74_1364_1523_1674_1589.png2.97±0.82 0.71±0.13images/BZ_74_1686_1523_1994_1589.png0.43±0.09 0.22±0.03images/BZ_74_1994_1523_2276_1589.pngimages/BZ_74_204_1656_422_1722.pngDCP模型DLS模型images/BZ_74_422_1656_708_1722.pngimages/BZ_74_708_1656_1023_1722.pngimages/BZ_74_1035_1656_1364_1722.pngimages/BZ_74_204_1788_422_1855.pngimages/BZ_74_422_1788_708_1855.pngimages/BZ_74_708_1788_1023_1855.pngimages/BZ_74_1364_1656_1674_1722.pngimages/BZ_74_1686_1656_1994_1722.pngimages/BZ_74_1994_1656_2276_1722.pngimages/BZ_74_1035_1788_1364_1855.pngimages/BZ_74_1364_1788_1674_1855.pngimages/BZ_74_1686_1788_1994_1855.pngimages/BZ_74_1994_1788_2276_1855.png0.79±0.16 0.36±0.12

在轴向载荷及弯曲载荷作用下，骨折端位移量比较由大到小依次为DCP模型＞DLS模型＞LCP模型，组间比较差异均有统计学意义（P＜0.05）。在扭转载荷作用下，LCP模型的位移量显著小于DCP模型和DLS模型，差异有统计学意义（P＜0.05）。DCP模型位移量显著大于DLS模型，差异有统计学意义（P＜0.05）。

2.2 应力测量结果

轴向载荷下骨折端内固定的应力分布见图2。在相同载荷量作用下，弯曲载荷产生的应力最大，其次为轴向载荷和扭转载荷，差异均统计学意义（P＜0.01）。而三种内固定模型之间比较显示，在轴向载荷及弯曲载荷作用下，骨折端内固定应力由大到小依次为DCP模型＞DLS模型＞LCP模型，组间比较差异均有统计学意义（P＜0.05）。而在扭转载荷作用下，LCP模型中内固定应力显著大于DCP模型和DLS模型，差异有统计学意义（P＜0.05）。但DCP模型和DLS模型比较，差异无统计学意义（P＞0.05）（表3）。

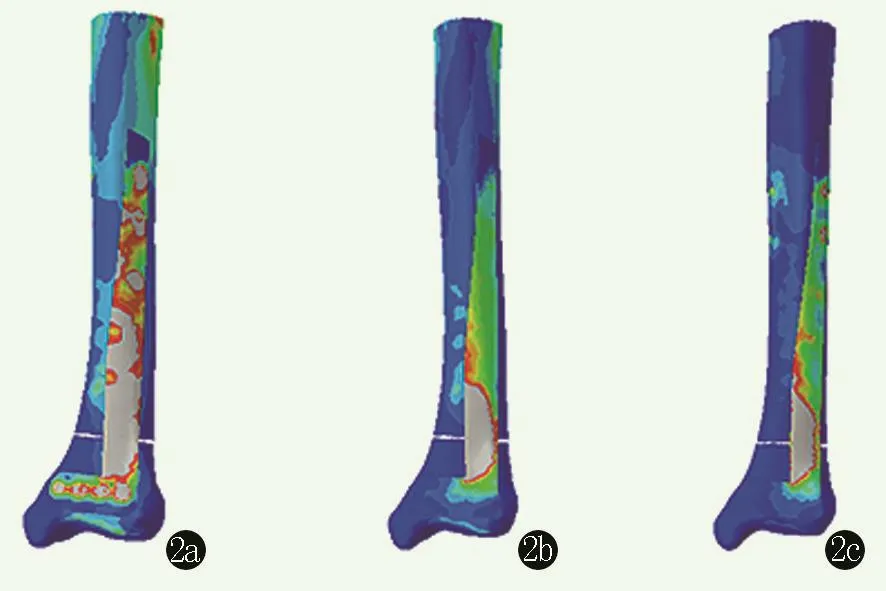
图2 轴向载荷作用下的内固定应力分布 2a:DCP模型，DCP钢板承担应力由近端开始向骨折部位逐步增加，并在骨折部位达到高峰，远端应力分布不均匀。高弹性模量的钢板形成严重的应力遮挡 2b:LCP模型，LCP钢板承担应力主要集中在骨折断端部位，两端分布较差 2c:DLS模型，DLS钢板在骨折近端及骨折断端存在应力集中，形成以远端为支点的杠杆作用，骨折端产生微动，降低应力遮挡率

表3 三种固定方式骨折端内固定应力（MPa，±s）与比较

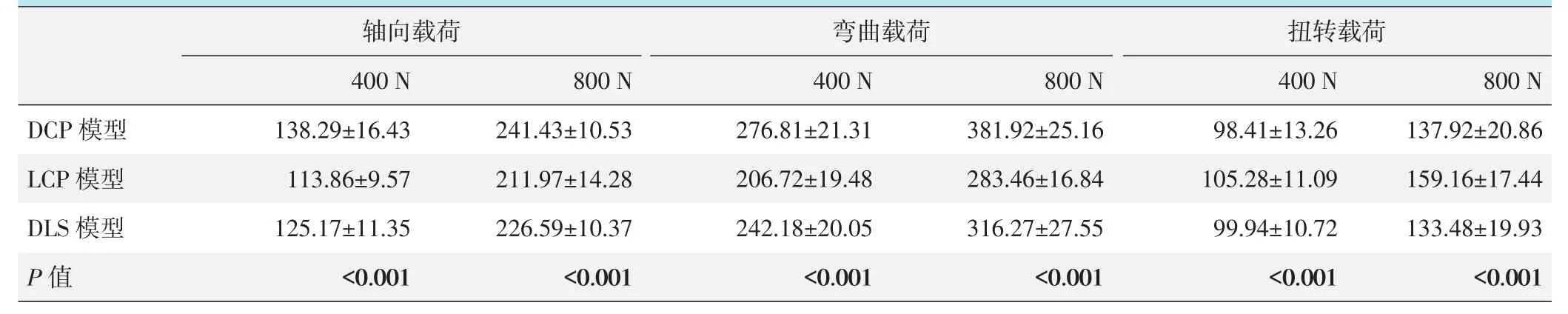
表3 三种固定方式骨折端内固定应力（MPa，±s）与比较

images/BZ_74_204_2445_425_2578.pngimages/BZ_74_425_2445_1046_2511.png138.29±16.43 125.17±11.35images/BZ_74_1058_2445_1683_2511.png276.81±21.31 242.18±20.05images/BZ_74_425_2511_747_2578.pngimages/BZ_74_747_2511_1046_2578.png241.43±10.53 226.59±10.37images/BZ_74_1697_2445_2276_2511.pngimages/BZ_74_1058_2511_1371_2578.pngimages/BZ_74_1371_2511_1683_2578.png381.92±25.16 316.27±27.55images/BZ_74_1683_2445_1697_2578.pngimages/BZ_74_1697_2511_1999_2578.png98.41±13.26 99.94±10.72images/BZ_74_1999_2511_2276_2578.pngimages/BZ_74_204_2644_425_2710.pngDCP模型DLS模型images/BZ_74_425_2644_747_2710.pngimages/BZ_74_747_2644_1046_2710.pngimages/BZ_74_1058_2644_1371_2710.pngimages/BZ_74_204_2777_425_2843.pngimages/BZ_74_425_2777_747_2843.pngimages/BZ_74_747_2777_1046_2843.pngimages/BZ_74_1371_2644_1683_2710.pngimages/BZ_74_1683_2644_1716_2710.pngimages/BZ_74_1697_2644_1999_2710.pngimages/BZ_74_1999_2644_2276_2710.pngimages/BZ_74_1058_2777_1371_2843.pngimages/BZ_74_1371_2777_1683_2843.pngimages/BZ_74_1683_2777_1716_2843.pngimages/BZ_74_1697_2777_1999_2843.pngimages/BZ_74_1999_2777_2276_2843.png137.92±20.86 133.48±19.93

2.3 应力遮挡率测量结果

应力遮挡为骨折内固定术后，因内固定装置的弹性模量与骨质的弹性模量存在较大差异，发生了应力、应变重新分配现象，表现为高弹性模量部分承担较多载荷，使低弹性模量部分分担较少载荷。本研究中将正常胫腓骨模型作为参照，对比轴向载荷中，骨折端应力遮挡效应的严重程度。结果显示三种内固定系统中，DCP模型的应力遮挡率为93.47%，LCP模型应力遮挡率为71.86%，DLS模型应力遮挡率为42.91%。

3 讨论

胫骨远端骨折为典型的干骺端骨折，手术内固定能够显著改善患肢功能。传统的DCP钢板通过螺钉的预紧力将钢板固定在骨面，螺钉与钢板之间为滑动接触关系。承受载荷时，应力经钉板之间的连接向下传导，应力会在钢板螺钉之间及钢板桥接处形成明显的应力集中和应变。本研究建立的胫骨远端骨折模型骨折间隙宽度为2 mm，按照单腿负重800N和双下肢负重400 N进行载荷模拟，结果显示DCP模型中骨折端位移量分别为（1.59±0.43）mm 和（2.73±0.61）mm。而弯曲载荷产生的位移量更显著大于轴向载荷，该分布范围显著高于骨折端的有效位移的0.2 mm～1 mm。进一步分析LCP模型和DLS模型中骨折端的位移量，结果显示同样载荷下，LCP模型的位移量最小，分别为（0.16±0.05）mm和（0.28±0.13）mm，该结果充分显示LCP固定系统中角度稳定机制的优势。在LCP模型中钢板与螺钉之间为共节点连接，以模拟实际工作中的钉板之间的锁定关系，使所有螺钉与钢板之间形成一个整体。在LCP模型中，载荷产生的微动源于钢板自身的应变，这就会出现钢板近侧骨皮质的微动小于钢板对侧骨皮质的微动现象，并可能导致近侧骨皮质的愈合不良。而在DLS模型中，对螺钉近端的设计进行了优化，即将锁钉近端螺纹去除，使之改变为螺杆，本研究中螺钉近端与近侧皮质骨螺孔之间不建立接触关系，螺钉与钢板之间及螺钉远端与皮质骨之间仍建立共节点关系，这样在充分发挥LCP优势的同时，能够在一定程度增加钢板侧骨皮质的微动范围，结果显示DLS模型中骨折端微动范围为分别为（0.52±0.11）mm 和（0.86±0.12）mm。

内固定系统的有效性，主要反映在骨折端稳定状态和应力遮挡情况。本研究以骨折断端上下螺钉及骨折端钢板的应力为观察应力集中程度程度的指标，结果显示在轴向载荷及弯曲载荷作用下，骨折端内固定应力由大到小依次为DCP模型＞DLS模型＞LCP模型，而在扭转载荷作用下，LCP模型中内固定应力显著大于DCP模型和DLS模型，但DCP模型和DLS模型之间差异无显著性意义。进一步研究显示DCP模型的应力遮挡率为93.47%，LCP模型应力遮挡率为71.86%，DLS模型42.91%。该结论与赵新文［7］的标本力学实验结果相一致。笔者认为主要原因是DCP中为保持固定稳定，螺钉需添加较大的预紧力，使骨骼成为内固定钢板的一部分，这样承受的载荷大部分通过钢板两端的螺钉进行传导。但在LCP中螺钉与钢板为绑定关系，螺钉之间应力分布较为均匀，所以应力遮挡率显著降低［1］。

综上所述，动态锁定螺钉钢板系统治疗胫骨远端骨折，能够为骨折愈合提供良好的力学环境，促进骨折断端内外骨痂的形成。但现有文献报道样本量较小，且患者具体情况复杂，临床疗效有待进一步观察。