空管供配电系统可靠性分析

廉永乐

（民航宁夏空管分局，银川 750009）

0 引言

近年民航空管系统各类业务不断开拓，通信、导航、监视设备日益增多，对供配电系统可靠性提出了越来越高的要求。供配电系统如何在现有设备条件下优化配置，减少系统单点瓶颈，提高系统供电可靠性，对保障空管各类业务具有重要意义。

供配电系统可靠性分析可以计算出系统中各设备或元件故障后系统故障的概率，系统故障后哪些设备故障概率较大，以及系统或其中某个设备发生故障的概率。一方面，可靠性分析可以帮助优化系统结构，合理配置冗余，减少系统单点瓶颈，提高系统可靠性；另一方面，可靠性分析还可以识别系统的薄弱环节，帮助判别可能发生的故障模式和原因，指导故障诊断和日常维护。

故障树分析法和贝叶斯网络分析法是系统可靠性分析的两种常用方法，采用基于故障树的贝叶斯网络分析法一方面可以较灵活地表达不确定信息，另一方面可利用其进行不确定性推理。

1 故障树分析法

在某个不希望发生事件的基础上建立一种特殊的方法，利用演绎方法将各种可能的原因事件寻出至最基本事件，即故障树分析法[1-3]。方法中所运用的定性分析和定量分析即为故障树方法的建立与求解。其中故障树的定性分析是本课题顶端事件的逻辑表达按一定规则被分解为基本的最小割集；而故障树定量分析则是利用已给定基本事件发生的概率，运用所知概率计算顶端事件发生的概率。

1.1 故障树分析方法步骤

故障树分析步骤如图1所示。

图1 故障树分析步骤

基于空管供电部分系统实例建立故障树模型和空管供电部分系统，如图2所示。根据图2建立供电系统故障树，如图3所示。

图2 供电系统

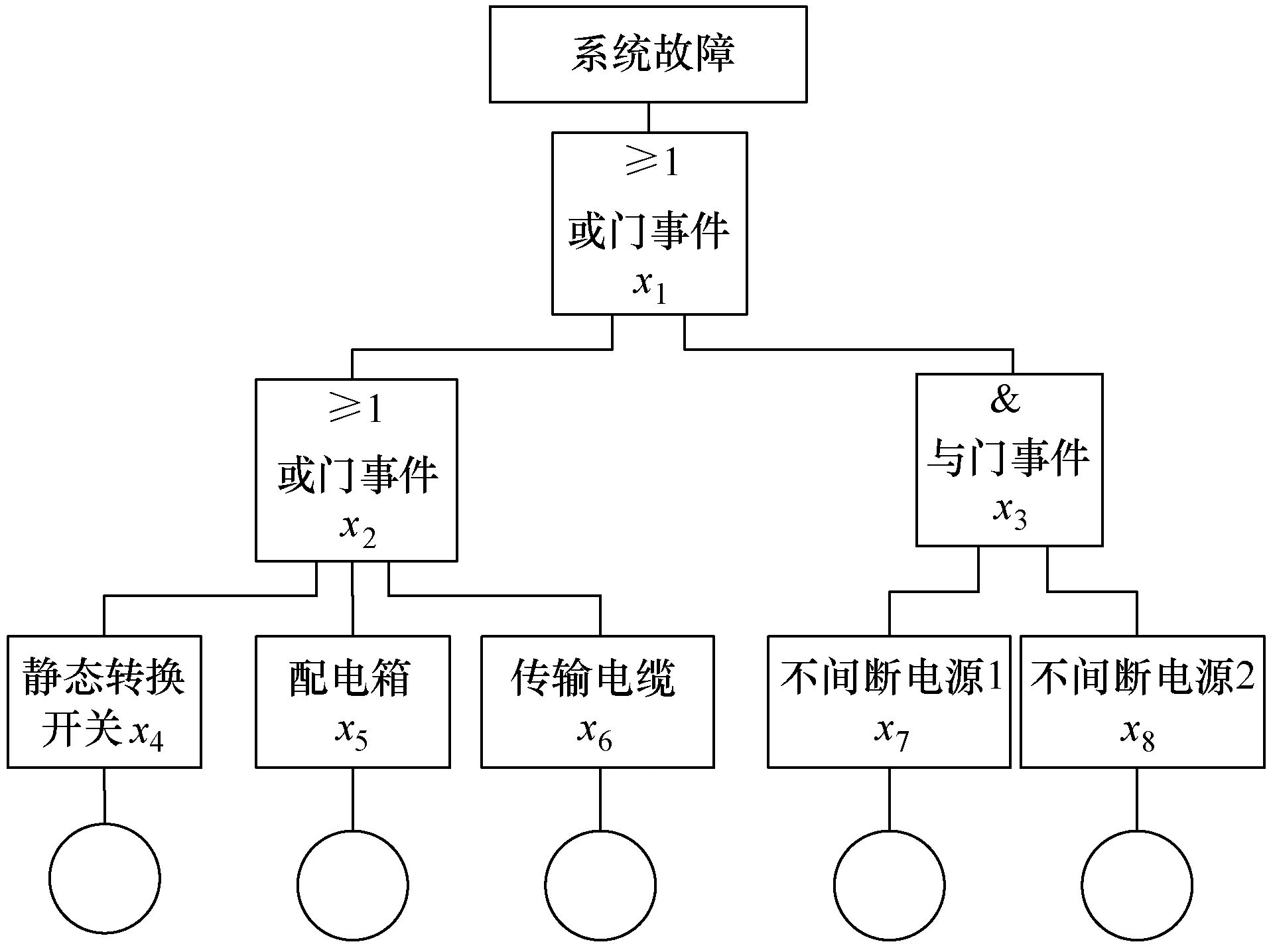
图3 供电系统故障树

1.2 故障树的定性分析

故障树定性分析需要求出所有的最小割集，上行法是目前求解最小割集比较常用的方法[4-6]。上行法的计算过程如下。

图3供电系统故障树的最下一级可表示为

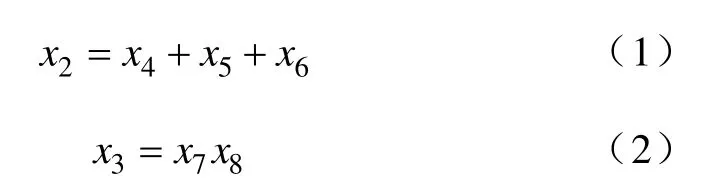
利用式（1）和式（2），上一级可计算为

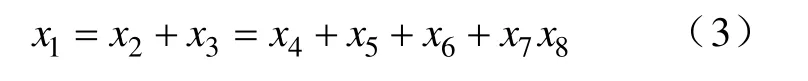
因此可得到故障树的四个最小割集，分别为{x4},{x5},{x6},{x7,x8}。

1.3 故障树的定量分析

故障树分析方法求解顶事件概率的方法是先计算各最小割集，然后将最小割集进行不交化处理，最后根据经不交化处理后的最小割集计算系统故障概率[7]。然而不交化处理非常繁琐，所以一般在故障树分析法中，将顶事件概率约等于所有最小割集概率的和。

故障树分析法在电力系统工程领域中识别系统的薄弱环节，主要是利用元件的“概率重要度、结构重要度、关键重要度”三个方面[8-10]，但电力系统结构较为复杂，建立系统可靠性指标和元件参数间的解析式及偏导较难，重要度分析法对系统薄弱环节进行识别的利用较难运用其中。

2 贝叶斯网络分析法

由于故障树分析法识别复杂系统的薄弱环节比较困难[11-12]，本文提出一种新的可靠性分析评估方法——基于故障树的贝叶斯网络分析法。贝叶斯公式是贝叶斯网络分析法的基础，即

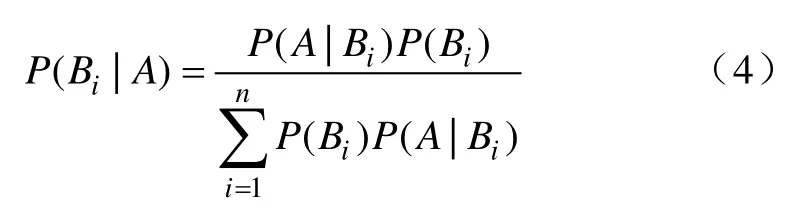
式中：P(Bi)为边缘概率；P(Bi|A)为条件概率。

贝叶斯网络分析法可以运用一个带有条件概率表的有向无环图来表达[13-14]。贝叶斯网络的结构表达两个方面的内容，分别是定性知识和事件间的因果联系。贝叶斯网络的边缘概率和条件概率表达了定量知识和原因对结果的影响程度。

利用已建立的故障树来建立基于故障树的贝叶斯网络，通过基于故障树的贝叶斯网络求解供电系统可靠性指标和识别系统薄弱环节。

基于故障树的贝叶斯网络供电系统拓扑，如图4所示。建立贝叶斯网络之后，通过求解贝叶斯网络获得系统故障概率和识别系统薄弱环节。基于故障树的贝叶斯网络可靠性指标的求解即求解边缘概率，其薄弱环节的识别是通过条件概率来实现的[15-16]。

图4 基于故障树的贝叶斯网络供电系统拓扑

以下基于供电系统拓扑实例来求解贝叶斯网络的边缘概率，假设x4、x5、x6、x7、x8故障概率分别为0.08, 0.1, 0.06, 0.02, 0.02。

3 空管供配电系统可靠性分析

采用故障树分析法和基于故障树的贝叶斯网络分析法分别对空管供配电系统可靠性进行分析计算，通过求解供电系统可靠性指标和最小割集，对供电系统薄弱环节进行识别，以优化供配电系统结构，提高供配电系统可靠性。

首先，根据日常维护经验，假设基本事件故障概率分别为，市电Ⅰ（P=0.2）、市电Ⅱ（P=0.2）、自动转换开关（automatic transfer switch, ATS）（P=0.066 7）、静态转换开关（static transfer switch,STS）（P=0.05）、油机（P=0.05）、集中不间断电源（uninterruptible power supply, UPS）（P=0.05）、集中UPS电池（P=0.10）、配电箱（P=0.055 6）、小UPS（P=0.1）、小UPS电池（P=0.1）、负载母线同步控制器（load bus synchronization, LBS）并机板（P=0.02），以上事件均以年故障概率计算。

其次，运用故障树分析法建立空管供配电系统故障树模型如图5所示，最后，根据建立好的故障树模型建立贝叶斯网络模型如图6所示。

通过计算机编程对空管供配电系统采用故障树分析法和贝叶斯网络分析法分析计算，得到相关数据见表1～表5。

由表1可发现，故障树分析方法与基于故障树的贝叶斯网络分析法两种可靠性分析法所得的失效概率基本一致。采用故障树分析法和基于故障树的贝叶斯网络分析法所计算得到系统可靠性指标分别为0.109和0.108，误差在0.1%。由此也说明基于故障树的贝叶斯网络分析法进行可靠性分析是可行的。

表2是在给定终端“用户设备”故障条件下，供电系统各元件发生故障的概率。由表2可发现，在给定终端“用户设备”供电故障条件下，供电系统中各元件故障概率较高的是：配电箱，2或门，STS Ⅱ，市电Ⅰ，市电Ⅱ，小UPS，5或门，集中UPS电池，小UPS电池，STS Ⅰ。

P（自身）是指在未设定证据变量的条件下各元件的可靠性指标。通过表2可发现在设定证据变量和未设定证据变量两种条件下，供电系统中各元件故障概率变化较大的是：配电箱，2或门，STS Ⅱ，小UPS，5或门，6或门，STS Ⅰ。

图5 空管供配电系统故障树模型

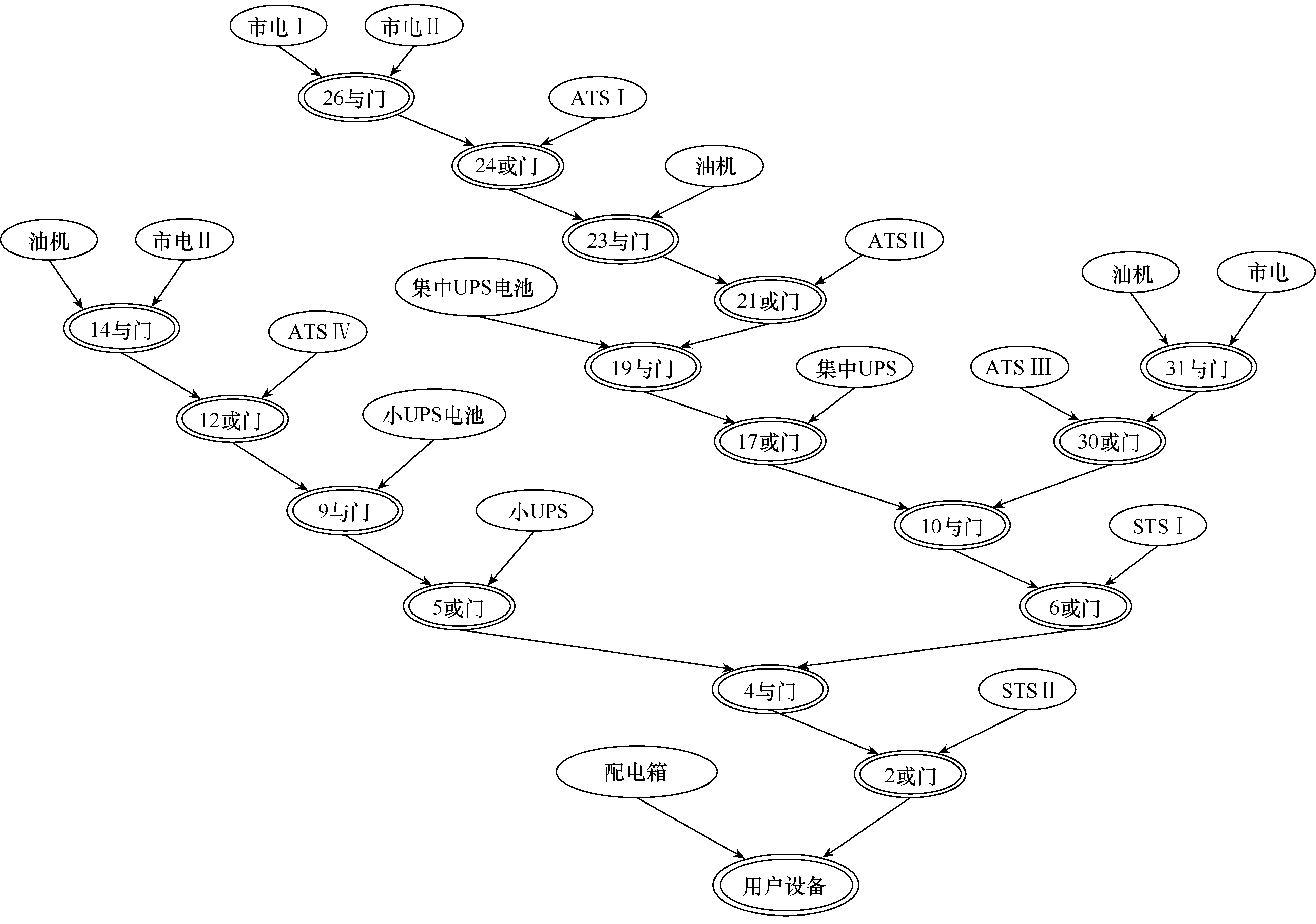
图6 基于故障树的贝叶斯网络模型

表1 两种可靠性分析法对比

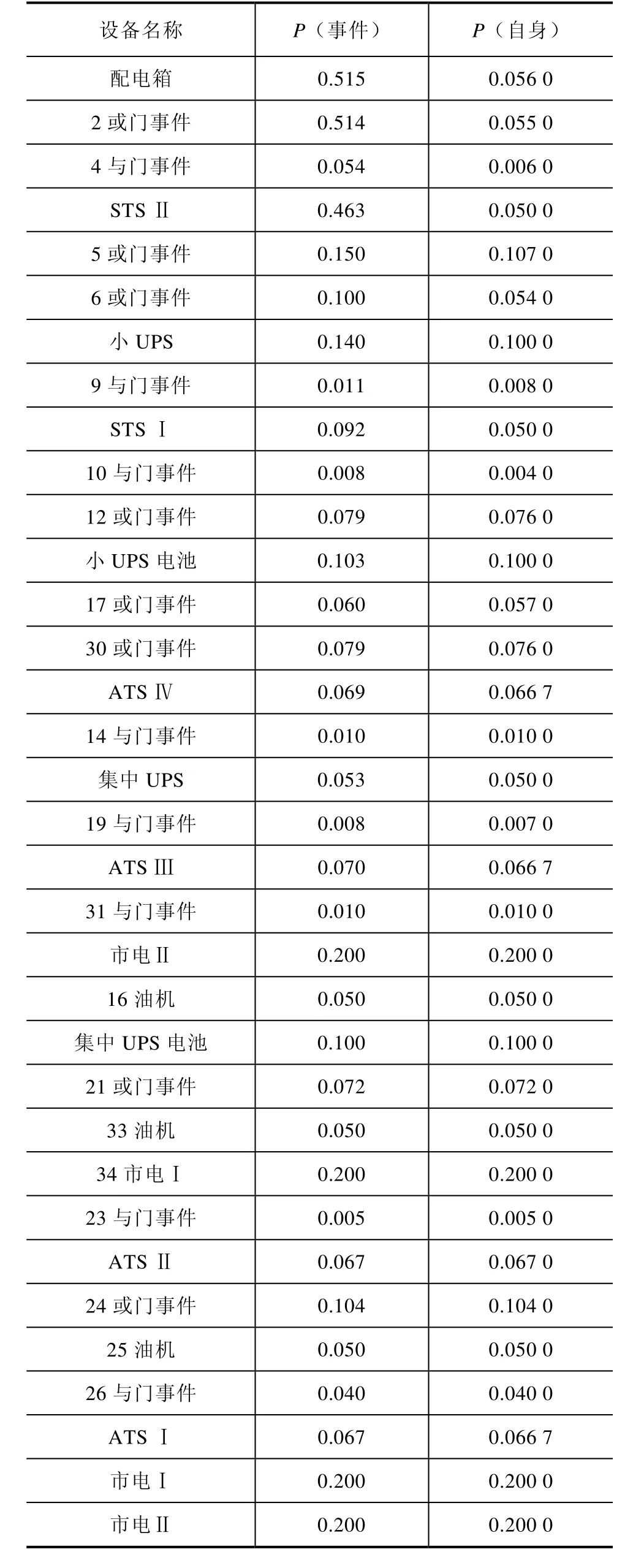
表2 给定系统失效时各元件失效的概率

其中市电Ⅰ、市电Ⅱ、油机，在两种条件下，故障概率基本没有发生变化。可以判断这些设备的故障概率变化对“用户设备”停电故障概率变化影响不大。

表3是在给定供电系统中各主要元件分别故障条件下“用户设备”停电的概率。同样，观察表3可发现在给定供电系统中各元件分别故障条件下“用户设备”停电概率较高的是：配电箱，STS Ⅱ，小UPS，STS Ⅰ，小UPS电池，集中UPS，ATS Ⅳ，ATS Ⅲ。

表3 给定各元件失效时系统失效的概率

P（原）是指在未设定证据变量的条件下，“用户设备”停电的概率为0.108。通过表3可发现在设定证据变量和未设定证据变量两种条件下，供电系统可靠性指标变化较大的是：配电箱，STS Ⅱ，小UPS，STS Ⅰ，集中UPS。其中，ATS Ⅳ、ATS Ⅲ、小UPS电池变化较小，市电Ⅰ、市电Ⅱ、油机基本没有变化。

表4是结构重要度分析，是在假定各基本事件发生概率相等均为0.5的条件下，分析各基本事件的发生对顶事件发生的影响程度。由表4可发现在供电系统中各元件概率均为0.5的条件下，设定证据变量“用户设备”停电概率P=1后，供电系统中各元件故障概率变化较大的是：配电箱，STS Ⅱ，小UPS，STS Ⅰ，ATS Ⅲ，小UPS电池，集中UPS，ATS Ⅳ。其中市电Ⅰ、市电Ⅱ和油机基本没有变化。

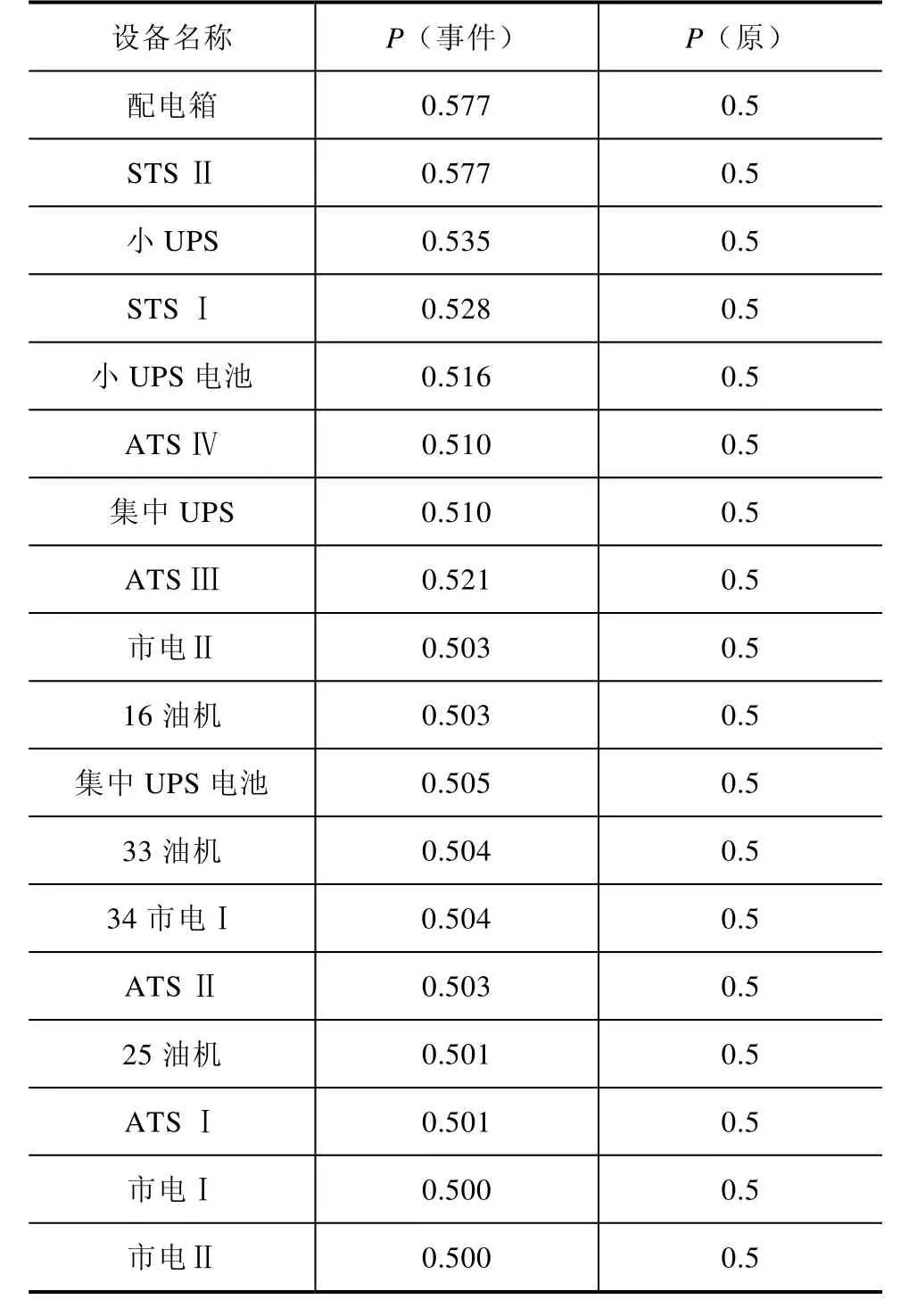
表4 结构重要度分析

综合表2、表3、表4分析得出“空管供配电系统”的薄弱环节为：配电箱，STS Ⅱ，小UPS，STS Ⅰ，ATS Ⅲ，小UPS电池，集中UPS，ATS Ⅳ。

由于配电箱和STS Ⅰ自动转换开关是供电系统的两个单点瓶颈，其可靠性直接决定着系统的可靠性。同时，仅从故障概率来考虑，单点设备和末端设备对一个系统可靠性具有直接作用，影响较大。但是从对系统的重要性和功能作用考虑，特别是故障后的可恢复性，单点设备和末端设备的作用就相对较小了。相反，作为一个系统的基础资源（如市电），其重要性和功能作用很明显，也很重要。一旦故障，其恢复相对于配电箱和STS要困难得多。虽然它对系统可靠性影响较小，但却是系统不可缺少且很重要的一部分。配电箱和STS虽然对系统可靠性影响较大，但却不会明显影响系统的功能，特别是在故障后能够快速恢复。

排查系统故障时，熟悉系统最小割集对查找和判断系统故障原因具有很大帮助，特别是对把握事故发生的规律、制定相应应急措施，具有指导意义。一个最小割集代表一种故障模式，故障模式代表系统发生故障的一种可能，最小故障模式越多表明系统越危险。通过最小故障模式，可以查找系统中的薄弱环节，并根据各故障模式对系统潜在风险作出直观判断，有利于风险预测和预防，同时还可以帮助事故调查。

由表5数据可知，空管供配电系统共有六种故障模式，其中，{No1：配电箱}，{No3：STS Ⅱ}为单点割集，且故障概率较高。{No7：STS Ⅰ与No8：小UPS}事件的组合故障概率次之，为0.005。其他三种故障模式故障概率较低。

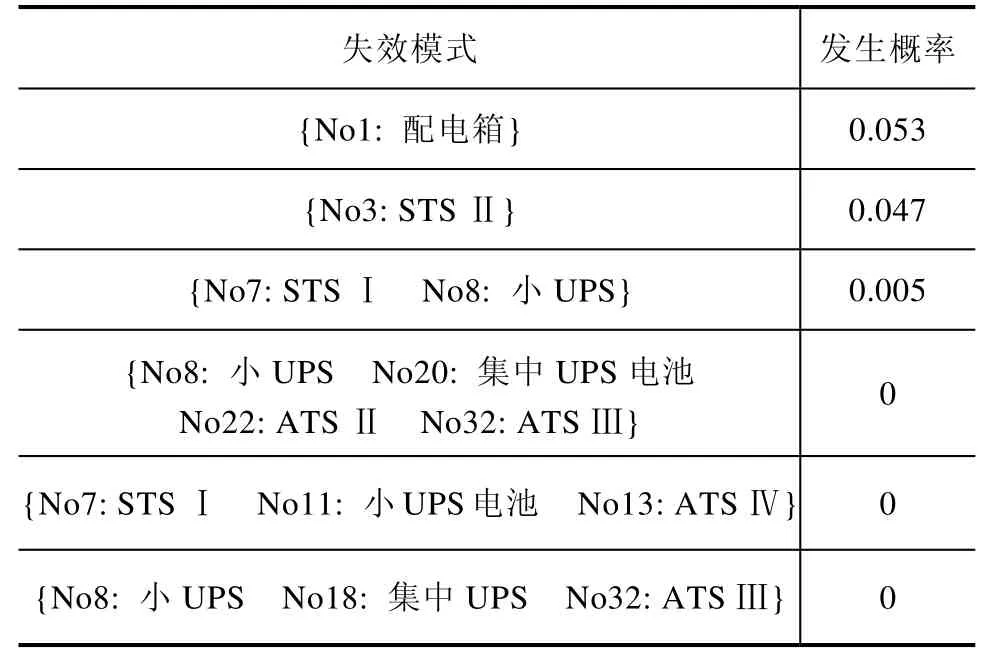
表5 供配电系统最小割集

4 可靠性分析的启示

通过以上分析可知，若要优化供配电系统，提高系统供电可靠性，降低事故风险，需要从以下三个方面改进提高。

1）从提高薄弱环节设备可靠性考虑。提高薄弱环节设备，特别是单点瓶颈设备的可靠性。

2）从优化系统结构，合理冗余、备份，消除单点瓶颈考虑。对单点瓶颈进行“并”处理，将用户端设备分散供电，降低因单点瓶颈故障造成的大面积停电风险。只有从根本上消除供电系统单点瓶颈，才能够大幅度提高系统可靠性，惟一的办法是用户端设备进行冗余。

3）从保障、维护的角度考虑。对薄弱环节设备储备相应的备件，以供故障后备份使用。对薄弱环节设备制定相应的巡视、巡检制度。对薄弱环节设备可能引发的各种故障编写相应的应急预案。熟悉系统中的所有最小割集，并编写针对每一种故障模式的应急预案。

5 结论

本文通过对空管供配电系统进行可靠性分析得出，基于故障树的贝叶斯网络分析法可让不确定信息能够较灵活地被表达，并利用其进行不确定性推理。将故障树转换成贝叶斯网络进行计算具有两方面优点：①可不考虑不交化计算过程；②可不运用最小割集的求解，计算和分析过程更为直观、灵活。运用基于故障树的贝叶斯网络分析法，能够监视系统中任何不确定性变量，不仅可以求出系统的故障概率，且各种条件概率也可被直接计算得出。在此基础上可为研究人员提供更加客观的推理判断分析，找出系统中存在的薄弱环节，从而有针对性地增强系统的可靠性。