基于二阶滑模控制的定频Buck数字电源设计

侯元祥 巫庆辉 蔡健哲

（渤海大学控制科学与工程学院，辽宁 锦州 121000）

0 引言

随着电源领域及微机控制技术的高速发展，数字电源受到了越来越多人的关注，数字控制具有灵活、基准调节简单、精度高等优势，正逐渐取代传统模拟控制[1]。数字电源的工作点不定，对输出的瞬态响应要求比较高，常规线性控制器是基于小信号模型设计的，被控变换器只有在特定条件下才能工作在最优状态，因而对于工作范围较宽的数字电源，无法利用传统的局部线性化方法进行控制器设计。滑模控制通常具有出色的大信号处理能力，将其应用在DC-DC变换器中，可以使电力电子变换器在更大的工作范围内具备较高的性能[2-3]。

滑模控制在DC-DC变换器中的首次应用出现于1983年Bilalovic等人发表的文献[4]中，作者论证了在降压变换器（Buck）中使用滑模控制的可行性，随后的30多年，该领域得到了长足发展。目前该领域主要可分为两个大方向：可变频率控制与固定频率等效脉冲宽度调制（pulse width modulation,PWM）控制。

理想滑模控制器需要工作在无穷大频率处，因而可变频率滑模控制器更加易于实现，其中具有代表性的方法有滞环滑模控制器[5]、电压电流混合滑模控制器[6-7]、分数阶滑模控制器[8]等，但由于开关频率不固定，变换器中储能电感与滤波电容的参数选取比较困难，且很难解决印制电路板（printed circuit board, PCB）设计中的电磁干扰、高次谐波吸收问题。

为了解决上述问题，有学者提出了定频滑模控制器，其中包括自适应滞环滑模控制器[9]、PWM等效滑模控制器[10-11]、定频模糊逻辑滑模控制器[12]等。此类控制器严格意义上属于间接滑模控制器，滑模控制律最终会等效为功率器件的占空比。该方法解决了开关频率不固定的问题，但等效控制概念的引入降低了滑模控制器鲁棒性和调节性能。文献[13-15]提出了具有积分项及二重积分项的滑模控制器，进一步提高了间接滑模控制器的稳态性能，并给出了在Buck变换器中的仿真结果。

为了进一步提高控制器动态性能、减小系统超调，本文基于定频积分滑模控制器的原理，增加误差的二阶导数作为附加滑模面，构成二阶滑模控制器。此外，实验中发现，受输出电压纹波及采样电路的噪声影响，采用差分求取导数信息的方法极易受高频噪声干扰，致使导数信号的信噪比较低，因此本文利用高阶跟踪微分器（tracking differentiator,TD）来获得输出电压的各阶导数。

1 同步Buck电路数学模型的建立

同步Buck电路拓扑如图1所示，采用两个电力电子器件Q1、Q2作为开关，工作时两个开关管处于互补状态，相比于传统Buck电路，同步Buck电路无续流二极管，可以提高效率，此外利用金属氧化物半导体场效应晶体管（metal oxide semiconductor field effect transistor, MOSFET）双向导通的特性，同步Buck电路在全状态下均工作于电感电流连续模式（continous conduction mode, CCM），对于控制器的设计更加有利。

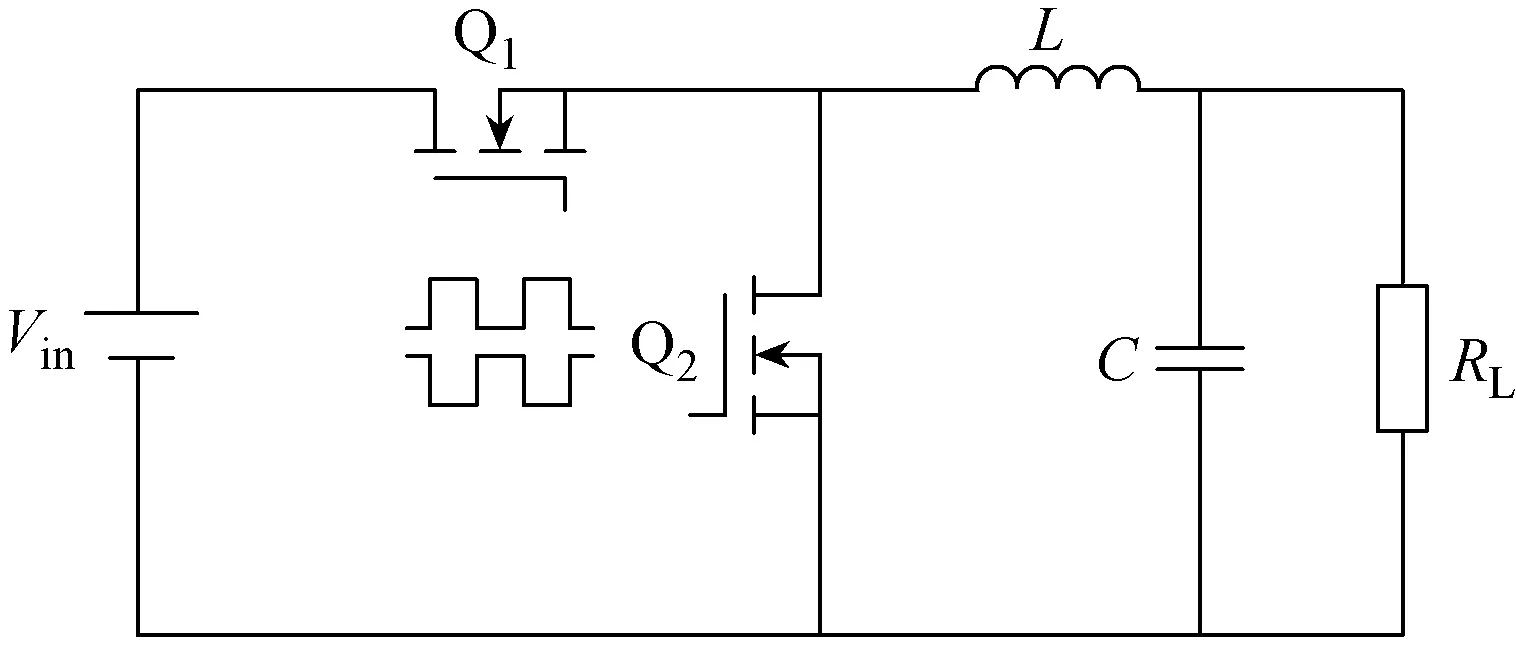
图1 同步Buck电路拓扑

采用状态空间平均法进行建模，引入开关变量u，当Q1打开、Q2关闭时，u=1，反之则u=0。取x1为电感电流，x2为电容电压，得到Buck电路的系统状态方程[7]为

式中：Vin为电源电压；L为Buck电路储能电感；C为储能电容；RL为负载电阻。该系统属于典型的时变系统，系统状态受负载电阻及开关状态影响。

2 定频积分滑模在Buck电路中的应用

严格意义上的滑模变结构控制器需要工作于开关频率无穷大的状态，为了固定开关频率，通常利用等效控制原理，对滑模控制律进行间接变换，使之适用于传统的定频PWM控制。此时控制器属于准滑模控制，为了保证等效控制律的性能，通常额外增加积分环节[12-13]，即滑模面由误差、误差一阶导数、误差积分项组成，则有

式中：x1为电压误差；x2为电压误差变化率；x3为电压误差的积分；Vout为Buck电路输出电压，忽略电容C的内阻，则此处Vout=VC，将式（1）代入式（2），得到Buck电路的状态空间方程为

整理成标准形式为

滑模面瞬时状态轨迹可描述为

式中，J=[a1a2a3]，a1、a2、a3均为滑动系数。

为了得到等效控制律，需要将式（3）对时间的导数设为0，利用不变性条件[10]求出等效控制信号ueq，它是离散开关变量u的等效平均值，同时等同于功率器件PWM的占空比，令JAx+JBueq+D=0，得到等效控制函数为

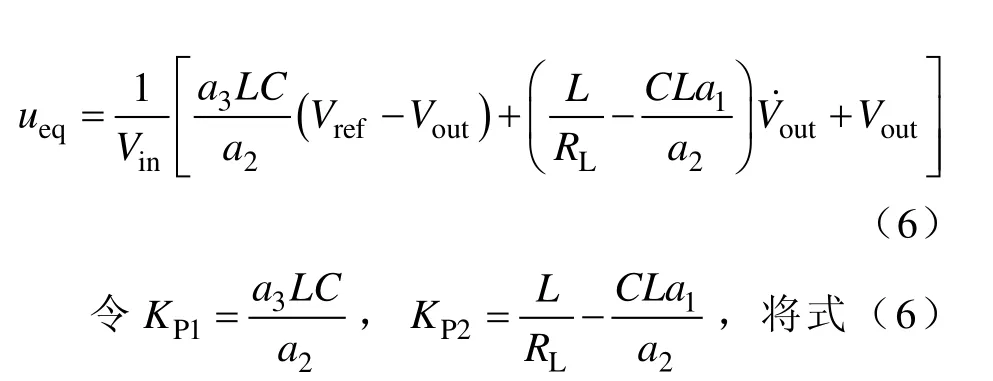
表述为控制框图形式如图2所示。

图2 Buck电路一阶滑模控制框图

图2中，β1、β2为分压网络的补偿系数，可以看出，等效后的滑模控制律，与传统的比例微分（PD）控制器类似，但是多了输入电压Vin与输出电压Vout分量，这些分量的出现归因于附加积分滑模面的作用及反馈的非线性，因此，相比于传统的线性控制器，滑模控制器可以在较宽的工作范围内仍然保持控制器的鲁棒性。

2.1 改进后的二阶积分滑模控制器

数控电源通常不具备真正的稳态工作点，其输出电压及负载范围跨度非常大，经过仿真分析发现，在某些工作状态下，传统的滑模控制律在应用过程中存在超调、误差收敛慢的现象，由于增加控制器的阶数通常可以改善系统的动态性能，所以本文对传统的滑模控制器进行了改进，增加了误差的二阶导数作为附加滑模面，改进后的二阶滑模控制器结构为

将式（1）代入式（7），得到状态空间方程为

利用不变性条件得到改进后的滑模控制器等效控制函数为

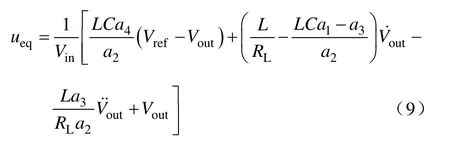
相比于传统的一阶滑模控制器，二阶滑模控制器其等效控制律中含有输出电压的二阶导数，从经典控制理论来看，引入高阶导数，会在系统闭环传递函数中形成零点，间接增加了系统的等效阻尼比，可以抑制超调以改善系统动态性能。

2.2 滑模控制器存在条件与稳定性分析

为了保证滑模控制器稳定，滑模系数必须满足滑模运动的存在条件，即局部可达性条件，如式（10）所示。

式（10）可以表示为

将式（8）代入式（11）进行求解，用u=1替换，u=0替换，得到滑模控制器的存在条件为

为了保证滑模运动的存在，滑动系数a1、a2、a3、a4应满足式（12）。

在满足滑模运动的存在条件后，为了保证控制器稳定，需要根据期望的动态性能来设计滑模系数，令滑模轨迹S=0，即

对式（13）两边取微分，可得到滑模轨迹方程为

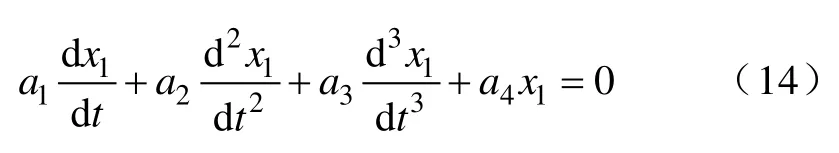
式（14）为标准的三阶系统，可根据主导极点的概念或借助线性系统分析工具进行分析与参数整定，进而获得期望的滑模轨迹动态性能，在此本文不做深入探讨。

2.3 线性跟踪微分器在滑模控制中的应用

由上述分析可知，二阶滑模控制的实现主要在于如何准确获得输出电压Vout的一阶导数及二阶导数，由于Buck电路本身存在输出电压纹波，电压采样过程又极易受放大器噪声及量化噪声影响，传统采用差分代替微分的方法得到的导数信息中含有大量噪声，因此本文将跟踪微分器应用到二阶滑模控制器中。

线性跟踪微分器的一般形式为[16-17]

式中：v、y为线性跟踪微分器的输入、输出；s为微分算子；r为跟踪微分器的速度因子，决定了跟踪微分器的带宽，取n=3时，可得到3阶跟踪微分器。将其写为状态变量表示为

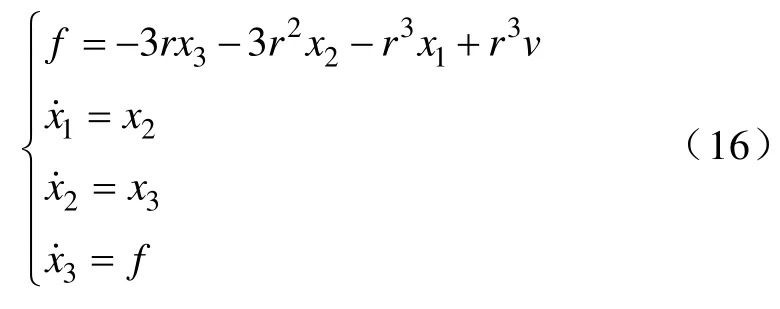
设采样步长为h，将其离散化为

式中，f为中间变量。当r取值合适时，可近似有

即通过式（18）可以得到输入信号的一阶导数与二阶导数。

图3为三阶线性跟踪微分器的仿真效果，输入信号为v(t)=sint的正弦信号，为了验证跟踪微分器的噪声抑制能力，原始信号加入幅值为0.004的白噪声，采样间隔h=0.001s，速度因子r=20。

图3 三阶线性跟踪微分器仿真效果

图3可以看出，跟踪微分器能较好地得到原始信号的各阶导数，滞后现象并不明显，且原始信号中的高频噪声没有被放大，相比于传统差分形式的微分器，线性跟踪微分器具有更强的噪声抑制能力，特别适用于从被噪声污染的原信号中提取微分信号。

3 样机搭建及结果分析

基于前文所述，改进后的Buck电路二阶滑模控制器框图如图4所示。

为了验证本文所提算法的可行性，搭建了Buck电路样机实验平台，如图5所示。

其中开关管容量为500V、20A，型号为IRFP460，主控芯片采用STM32G474单片机，该单片机具有170MHz的主频、硬件数学加速器、高分辨率PWM及16位模数转换器，适用于高精度数字电源控制。实验采用艾德克斯1 500W电子负载并利用其同步触发功能进行阶跃带载测试，利用USB总线将实验结果上传至PC进行数据绘制与分析，此外为了减小输入电压波动对控制器性能的影响，前端采用功率因数校正电路（power factor correction, PFC）进行稳压。Buck电路设计参数见表1。

图4 改进Buck电路二阶滑模控制器框图

图5 Buck电路样机实验平台

表1 Buck电路设计参数

为了综合考察电源的各项指标，实验过程覆盖整个电源的功率范围，包括空载与满载，期望输出电压及负载电流扰动情况如图6所示。

图6 期望电压与负载扰动电流波形

实验中模数转换器采样频率与PWM频率相同，为50kHz，线性跟踪微分器速度因子取r=15 000。图7为分别采用线性跟踪微分器与传统的向后差分法得到的输出电压导数信息结果对比。

从图7可以看出，由于采样过程引入了随机噪声，传统向后差分法得到的导数信息其信噪比较低，尤其是求取二阶导数信息时，噪声被严重放大，而跟踪微分器对于噪声抑制的效果较好，求得的导数信息受数据采样噪声的影响较小，且滞后现象并不明显，这对于后续滑模控制器的设计至关重要。

为了避免系统超调同时考虑到硬件上的限制，根据式（14），按照欠阻尼系统来设计滑动系数，为了横向对比控制器性能，取一阶与二阶滑模控制器中的系数KP1、KP2相等，其中KP1=0.019，KP2=−1.3×10−5，改进的二阶滑模控制器其二阶导数项系数KP3=−1.0×10−9。图8（a）为仿真过程输出电压波形，图8（b）为电源启动时0～5ms的局部细节，图8（c）为施加阶跃扰动时10～20ms的局部细节。

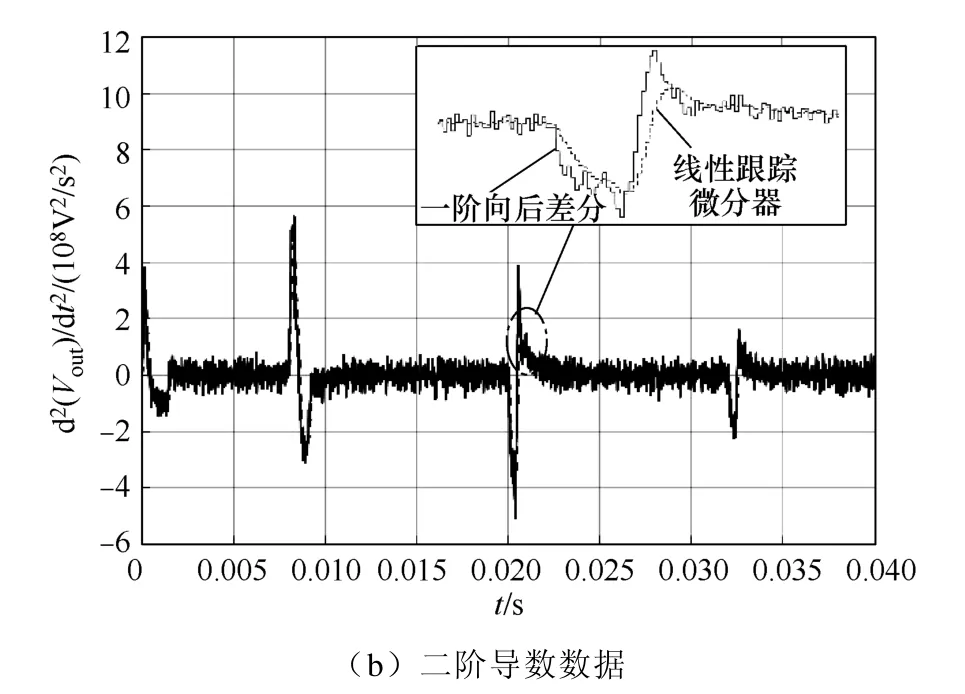
图7 输出电压一阶与二阶导数信息

图8 Buck电路输出电压响应曲线

动态性能对比见表2和表3。

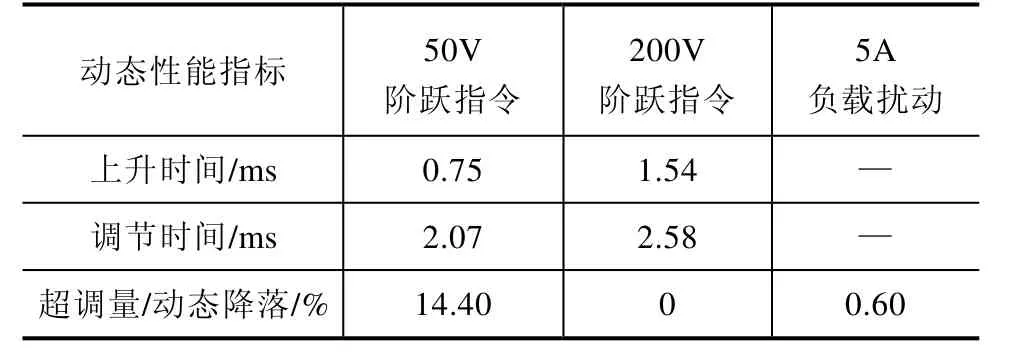
表2 一阶滑模控制器动态性能

由表2和表3可以看出，与传统一阶滑模控制器相比，改进后的二阶滑模控制器，在施加50V阶跃指令扰动时，输出电压超调现象消失，调节时间更短，200V阶跃指令扰动时，调节时间同样缩短，施加5A负载电流扰动时，电压跌落更低，动态效果更好。

综上所述，本文提出的二阶滑模控制器，控制性能更加优越，跟踪微分器的引入解决了实际过程中采样噪声对导数求取过程的影响，使其更具实际应用意义。

4 结论

本文针对同步Buck型宽工作范围数控降压电源，提出了一种二阶滑模控制器，其滑模面由电压误差、电压误差一阶导数、电压误差二阶导数、电压误差积分构成，并搭建了样机进行算法验证。实验结果表明，与传统一阶滑模控制器相比，二阶滑模控制器动态性能更好，解决了控制器的快速性与超调量之间的矛盾。

此外，本文引入了跟踪微分器的概念，用于获得输出电压的各阶导数信息，节省了额外的电流传感器，解决了传统微分器对于采样噪声敏感的问题，具有较高的实际应用价值。值得注意的是，滑模控制及跟踪微分器便于离散控制，对于数字控制系统比较友好，对于模拟控制系统则实现起来较为复杂。